Why did it take 100 years to find the exact value of the Planck constant?

Translation of Michael Trott's post " An Exact Value for the Planck Constant: Why Reaching It Took 100 Years ".
The code in the article can be downloaded here .
Many thanks to Polina Sologub for help in translating and preparing the publication.

---

Content

- Some thoughts on the occasion of World Metrology Day in 2016
- Introduction and a little about me
- From the origins of the metric system to the present day.
- An increase in the number of constants
- The existing SI system and the problem of kilograms
- New SI
- Second
- Moth
- Kelvin
- Ampere
- Candela
- Why are there 7 main units of measurement?
- Way to change the definition of kilogram

---

The narration is conducted on behalf of Jean-Charles de Bord.

Some thoughts on World Metrology Day 2016

Let me introduce myself:
I am a man of science and I love precision.
All this time I was somewhere nearby.
I took a pound and a toaz from people.
And I was next to Louis XVI.
In the moments of his doubt and pain.
I'm damn sure that metric roulette,
thanks to platinum standards will be established once and for all.
I am glad to meet you!
I hope you guessed my name?

Introduction and a little about me

If you haven’t guessed yet, I’m Jean-Charles de Borda : a sailor, mathematician, scientist and member of the Academy of Sciences. I was born on May 4, 1733 in the city of Dax in France. Two weeks ago, I celebrated my two hundred and eighty-third birthday. And here I am:



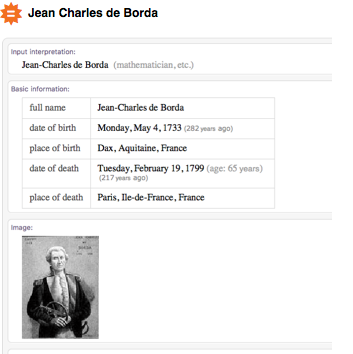
In my hometown, a monument was erected in honor of me. If you are nearby, pause to look at him. If you don’t know where Dax is, here is a map:



When I was a boy, France looked about the same as it is now. We had a little less territory on the east side, but in North America, my country owned a good piece of land:



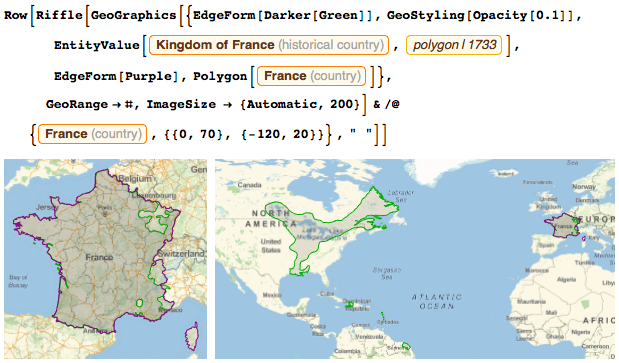
I led an interesting life. By the age of 32, I spent a lot of time on the high seas doing research. When I was forty, I already commanded several ships in the battles of the Seven Years War (although I still devoted most of my life to science).

I died on February 19, 1799 in Paris, and no one knows where my grave is (I know, of course, but I can’t talk about it). My name is immortalized on the north-east side of the Eiffel Tower:



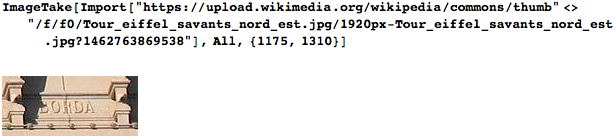
For centuries, many of my French colleagues, whose names joined mine, have told me that I deserve a place in the Pantheon. However, you will not find me either there or in the cemeteries of Pere Lachaise, Montparnasse or Montmartre.

But this does not bother me. I am a humble person; the problem with the standard kilogram does not let me sleep at night. True, soon I will be able to rest for all sleepless nights.

Let me tell you about it.

All my life I was engaged in mathematics, geometry, physics and hydrology. I liked the measurements. You may have heard about the voting system (Bord's method) - this is also my invention . I have also greatly improved the repeating circle . And this is where my story begins. The periodic circle was crucial in determining the exact size of the Earth (see discussion of my circle here ).



I lived in France during the monarchy. This time was difficult for many people, and especially for peasants. This was partly because trade and commerce were in decline due to the lack of a unified system of units of measure for the country as a whole. If you like reading on historical topics, I highly recommend you the book of Coulis People and Dimensions - you can imagine how things were with measurements (primarily weight and size) in France in 1790. A similar situation has developed in other countries (see the report of Johann Georg Thralles on the situation in Switzerland ).

In August 1790, at the initiative of Louis XVI, I became chairman of the Commission on Weights and Measures. And so far, I am concerned about the fact that 1000 years after Charlemagne's initiative to unify measures and weights, new work began in this direction. With the help of our commission, the metric system was created, which today is an international system of units, abbreviated SI (in French le Système international d'unités ).

The commission also included: Pierre-Simon Laplace (Laplace equations), Adrien-Marie Legendre ( Legendre polynomials), Joseph-Louis Lagrange ( Lagrange function), Antoine Lavoisier (formulation of the law of conservation of mass of matter), and Marquis de Condorcet (I always said Adrien Marie, what should he orderhis portrait , but he refused to say that he was too busy with calculations). Over the past decades, Adrien-Marie made friends with Jacques-Louis David , who painted a whole collection of paintings with him; unfortunately, none of the mortals will ever see them. Lagrange, Laplace, Monge , Condorcet and I were part of the original team (although Jerome Lalande was with us at the very beginning , and later Louis Lefebvre joined us ).



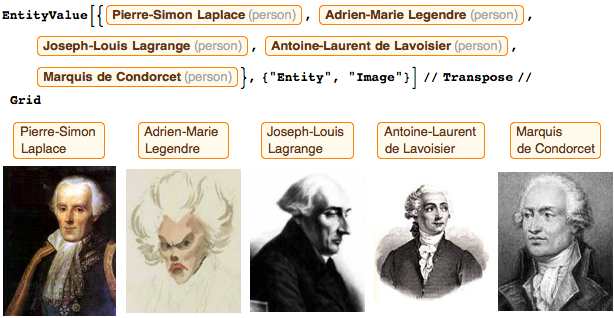
The three of us (Monge, Lagrange, and Condorcet) were buried or immortalized in the Pantheon. I really hope that one day Pierre-Simon, who deserves it, will join them.

As I already said, it was difficult for French citizens to live in this era. Laplace wrote :

In use is a monstrous number of units; they are inconvenient for calculation, they are difficult to compare; the difficulties that they make in trade cannot be considered without recognizing that the adoption of a measuring system (in which its single parts are easily calculated and which are obtained at least arbitrarily, and the units of measurement must be indicated by nature itself) will become one of the most important services that any government can provide to society. A nation within which a new system of measures will appear will be the first to reap the benefits of its advantages, and then other nations will begin to follow its example, for which it will thus become a benefactor; the slow but inevitable dominion of the mind, prevailing over national jealousy, will crown all the obstacles that are overcome, contrasting themselves with advantages.

All five mathematicians (Monge, Lagrange, Laplace, Legendre and Condorcet) made a historically significant contribution to mathematics. Their names are mathematical theorems, structures, and operations:





In 1979, Ruth Ines Champagne wrote a dissertation on the influence of five of my fellow citizens in the creation of the metric system (to learn more about Legendre's contribution, see the article by Doris Hellman ). It seems to me that today, most mathematicians are no longer interested in units of measure, and physicists are the driving force in this area. But I did, as in an article by Theodore P. Hillabout the method of combining probability distributions, which allows you to combine knowledge from various experiments (I’ll say right away that we have instant access to arXiv in the sky. I will say more: direct connection with arXiv has become the largest innovation of the last millennium).

Our task was to create unified units for measuring time, length, volume and mass. We needed such units of measure with which we could measure both tiny and astronomical objects. The principles of our approach were well summarized by John Quincy Adams , United States Secretary of State, in his 1821 book Weights and Measures Report .



Originally we (we called ourselves metric men) suggested only a few prefixes: kilo, deca, hecto, dec, santi, milli, and miria, which is no longer used (in some old books you can find examples of using a prefix meaning ten thousand).

This idea of ​​using prefixes arose quite early in the process of developing new units. Here are our suggestions for 1794:



At one time, we also used demi and double (demi-hectoliter (= 50 liters) or double decalitre (= 20 liters)).

Time, length, and mass, measured in physics, chemistry, and astronomy, span over 50 orders of magnitude. And the units we created in the turbulent era of the French Revolution have stood the test of time: In the future, for the SI, it may take a few more prefixes. In recently





At the open observatory LIGO, the length of the arms of the interferometer changed by approximately 10 yo-meters. Yoctogram mass sensors already exist. One yoctometer is 10 ^-24 meters. Mankind can already measure the tiny powers of the zeptonewton order. Astronomy

, on the other hand, needs prefixes more than 10 ²⁴ . And one day they can become official.



I am a person of strict rules. It drives me crazy when in the twenty-first century I see people who don’t follow the rules for using SI prefixes. Recently, I saw someone writing on a blackboard that a year consists of π decamegase seconds (π daMs):



Let it be even a good approximation (with a deviation of only 0.4%); only when this person finds out that prefixes should not be combined?

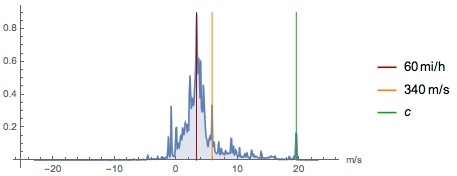
Technological progress over the past two centuries has been rapid. And the prefixes of mega-, giga-, tera- or nano-, pico- and femto- in the twenty-first century have become common. Below you see the probabilistic distribution of velocity values. Some speeds (for example, the speed of sound or the speed of light) are used more often than others, but many local maxima can be found in the distribution function:



Here is a report (which we provided in March 1791) that gave rise to the metric system and which described the conceptual meaning of meter and kilogram. It was signed by Lagrange, Laplace, and Monge (now accessible even through what the modern world calls a “digital object identifier”, or DOI, like 10.3931 / е-rara-28950 ):



Most people think that base 10 is closely connected to the meter , second and kilogram as units. However, we decided to use 10 as the basis for dividing units only on October 27, 1790. We seriously considered 12 as a basis, because divisibility into 2, 3, 4 and 6 was convenient for trading. Today, however, it is clear that we made the right choice. Lagrange was rightwhen he insisted that the number 10 be the basis. During the French Revolution, we made no compromises. And on November 5, 1792, I proposed converting the clock to a decimal number system (the D'Alembert suggested this back in 1754, see this article for details ). Mankind was not ready for such changes; perhaps in the twenty-first century, decimal hours will finally be recognized as much more convenient than 24 hours, 60 minutes and 60 seconds. Our decimal clock was beautiful . It was a real surprise for me that humanity still divides the angle by 90 degrees. In my periodic circle, I divided the right angle by 100 degrees.

We wanted to make the new units really equal for all people, and not to base them, for example, on the length of the king's forearm. In general, “for all times, for all peoples” ( “À tous les temps, à tous les peuples ). Now this dream will come true.

I’m sure that the day will come when Mendeleev’s predicted:

Let us facilitate the universal spread of the metric system, thereby contributing to the general well-being and the desired future rapprochement of peoples. It will not come immediately, but gradually and absolutely precisely.

will become a reality even in those 3 countries of the world that do not use this system:



SI units have been legally used in the USA since the mid-twentieth century, when the usual US units began to be derived from the definitions of the basic SI units. Citizens can choose which units they want to use for trading.

We also introduced decimal to the base of the monetary system, and our franc was in circulation from 1793 to 2002. Today, all countries have money in circulation based on the decimal system of calculation. Here is a “breakdown” of coin denominations by country:



We spoke very seriously about “all people”, as evidenced by our work with our sworn enemies - Great Britain and the new United States (through Thomas Jeffersonpersonally) to create a new system of units of measure for all major countries. But, as often happens, politics won in the battle of politics and reason.

I died on February 19, 1799, just a few months before the first successes of our group. On June 22, 1799, my dear friend Laplace made a speech about the creation of new units of length and mass even before the new samples were delivered to the archives of the Republic (where they are still located).

In case the reader became interested in my eventful life, Jean Maskart wrote in 1919 my biography, now available in the form of a reprint edition .

From the beginnings of the metric system to the present day

Two of my friends: Jean-Baptiste-Joseph Delambre and Pierre Meschen traveled to France and Spain to take measurements to determine the meter as one ten millionth of the distance from the North Pole to the equator of the Earth. I am glad that the mission has been approved. When Louis XVI approved the financing of the mission, he was already under arrest. My dear friend Lavoisier called his task “the most important mission that has ever been set before man .”



If you have not yet read Ken Alder’s book The Measure of All Things , I advise you to do it immediately. There is even a German filmabout the adventures of my two old friends. Armed with a special tool that I designed for them, they did the work that resulted in the creation of the meter. Despite the fact that we wanted to establish a meter length equal to one ten millionth of the length of the meridian passing from the pole to the equator through Paris, I think that today this beautiful definition is exclusively conceptual. We did not know at that time that the Earth was not completely round, and errors in the calculations of the flattening of the Earth led to a small but regrettable error of 0.2 mm. Here is the length of half the Paris meridian, expressed in meters:



If all the elevations were taken into account (which Delambre and Meshen did not do, because for this they would have to travel along the entire meridian to take into account each mountain and hill!), And 3D coordinates (including elevations of the terrain), their meter in ultimately, it would become shorter by 0.4 mm:



But the height profile along the Paris meridian:



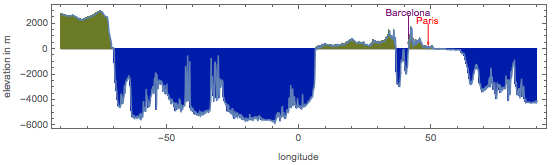
Because of the “fractality” of the Earth’s surface, if you take the measuring instrument even less, the error will increase significantly.

The meter will be 0.9 mm longer if measured with a ruler several hundred meters long:



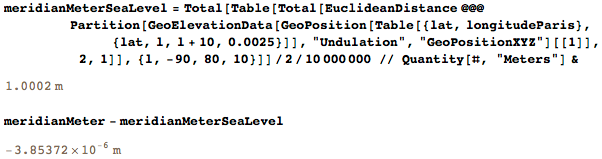
It would be more realistic to follow the height of the sea level. The difference between the obtained meter definitions is only a few micrometers:



At a minimum, the meridian had to go through Paris (and not through London, as some British scientists of my time suggested). But in any case, finding the length of the meridian was just a stepping stone to creating a meter. After we received the sample, the meridian no longer interested us.

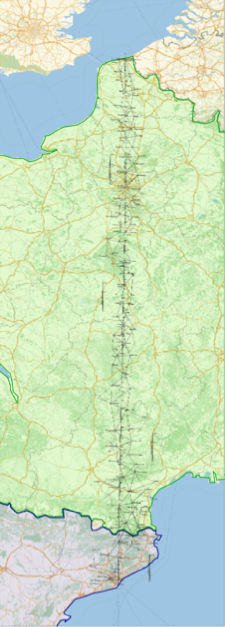
Here is a sketch of the triangulation conducted by Pierre and Jean-Baptiste during their adventurous six-year expedition. Thanks to the Internet and various French digitization projects, French-speaking readers interested in metrology and history can now read the results online and reproduce our calculations:



Part of the Paris Meridian(and the Paris Observatory, marked in red) are marked with a marker: do not miss them during your next visit to Paris! Francois Arago remeasured the Paris Meridian. In 1804, Laplace received money from Napoleon to re-measure the meridian to verify and improve our work:





When calculating the second, we started from the length of the year. And we removed a kilogram as a unit of mass from one liter of water. If any liquid is special, then of course it is water. Lavoisier and I argued a lot about the ideal temperature. There were two options: 0 ° C and 4 ° C. Initially, we thought about 0 ° C, because ice is easy to see. But then we chose 4 ° C, because it is at this temperature that the water reaches its maximum density. The transition to 4 ° C was proposed by Louis Lefebvre-Jean . We determined the volume of a liter as a cube of one tenth of a meter. After comparison with high-precision measurements of distilled water, 1 kg turned out to be 1.000028 dm ^{3 of} water. An interested reader can find much more detailed information about the process.water measurements and the creation of the original metric system. A more concise history in English can be found in a recent Williams book .

I do not want to boast, but we also came up with the name "meter" (derived from the Greek metron and Latin metrum ), which we proposed on July 11, 1792 as the name for the new unit of length.

To maintain historical accuracy, I want to note: until I entered the celestial spheres, I always thought that our group was the first to carry out such a thing. I was amazed when, shortly after my arrival, Ya-xing and Nanjing Yue told me about their expedition to determine the unit of length that took place from 721 to 725, that is, more than 1000 years before ours.

I am very glad that we defined the meter in this way. The original idea was to determine the meter using a pendulum of the correct length with a half-period of 1 second. But I did not want any changes related to the second to affect the length of the meter. Since a certain kind of dependency in the system of units is inevitable, they should be minimized.

At that time, the idea of ​​determining the meter based on the shape of the Earth, and the second on the movement of the Earth around the Sun, seemed good. It was even the best idea that we could implement at that time. We did not know how the tides and time changed the shape of the Earth, or how the continents moved away from each other. But we believed in the future of mankind, believed that the accuracy of measurements would increase, although we did not know what exactly would change. These were our first steps taken to accurately measure distances in France. Today we have high-precision geo-maps:



The best masters of my time smelted platinum, and we forged bars a meter long and kilogram samples. It was an exciting time. Twice a week I stayed with Marc-Etienne Janet- where he forged our first kilogram samples. The melting and shaping of platinum has not yet been worked out. Jeanette - the jeweler of Louis XVI - was a real master in working with platinum (to be completely accurate, with platinum lips). Just a few years earlier, on June 6, 1782, Lavoisier showed the melting of platinum in a hydrogen-oxygen flame to the future Tsar Paul I; the latter came on a visit to Marie Antoinette and Louis XVI. Later, Etienne Lenoir made our platinum meter, and Jean-Nicolas Fortin made a platinum kilogram. For readers interested in the history of platinum, I recommend the book by McDonald's and Hunt .

Platinum is a special metal: it is characterized by high density and chemical inertness. In addition, it is not as soft as gold. The best kilogram standards to date are made of platinum-iridium alloy (adding iridium to platinum really improves its mechanical properties ). The following is a comparison of some of the physical characteristics of platinum, gold, and iridium:



It sounds simple, but at that time the best scientists spent countless hours in calculations and experiments to find the best materials, the best forms and the best conditions for determining new units. But both the new meter and the new kilogram cylinder were macroscopic bodies. All macroscopic artifacts are difficult to transport (we have developed special cases for transportation); they change quite a bit even after 100 years of use, absorption and desorption, heating and cooling. As a result of the technological progress of the nineteenth and twentieth centuries, it has become possible to measure time, mass and length with an accuracy of one billionth. And measuring time can be done a billion times better.

I still remember very well that after we made new standards of length and mass, Lavoisier said: " nothing more majestic and simple did not go out of the hands of man ." I still think so.

Our goal was to create units that are convenient for everyone. Our motto was: "for all peoples - at all times." We have posted copies of the meter throughout Paris so everyone knows how long it was (next time you visit Paris, be sure to look at the mètre étalon next to the Luxembourg Palace). This photograph I recently found shows how an interested German tourist studies the history of one of the few remaining meter standards:



It was an exciting time (even if I was not there when the commission completed this work). Our units were used in most European countries in the nineteenth and most of the twentieth century. We created a meter, a second and a kilogram. Later, four more basic quantities (amperes, candela, moths and kelvin) were added to the results of our work. With these updates, the metric system has served humanity for more than two hundred years.

The graph below shows a sharp rise in the frequency of use of the words kilogram , kilometer and kilohertz in the books after the Metric Convention of 1875:



We determined only a meter, second, liter and kilogram. Today, SI includes many more units: becquerel, pendant, farad, gray, henry, hertz, joule, rolled, lumen, lux, newton, ohm, pascal, siemens, sievert, tesla, volt, watt and weber. Here is a list of dimensional relationships (no physical meaning is implied) between the derived units:





Many nominal units added after my death were mainly associated with electrical and magnetic phenomena that were not yet known in my lifetime. And although I'm generally a serious person, I love jokes and puns. However, I do not like it when they joke about units of measure. For example, there is such a system with units: potrzebie, ngogn, blintz, whatmeworry, cowznofski, vreeble, hoo and hah (a system introduced by Donald Knut(Knuth's Potrzebie system of units)). Not only are their names meaningless - their meanings also don't make sense:



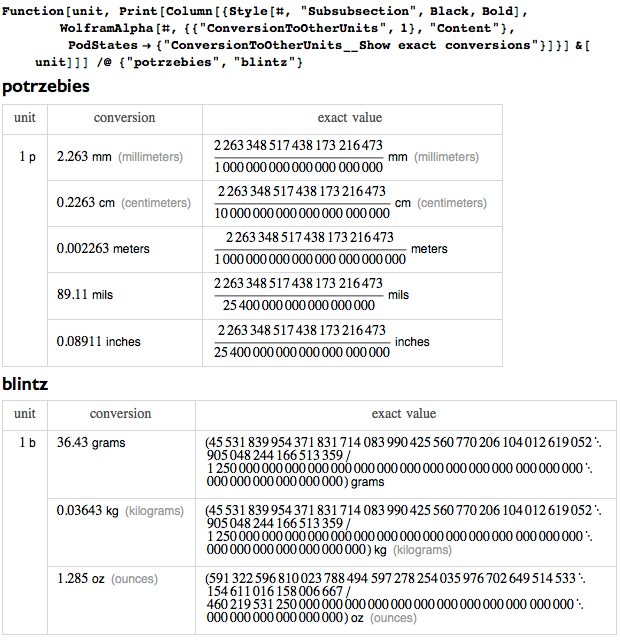
Or look at Max Peterson's suggestion for units of measure for biology . Unit names and prefixes may seem ridiculous, but units of measure are too serious for me:



These unit names do not even rhyme with any of the proper names:





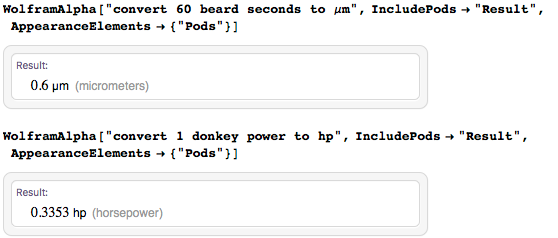
I repeat: I like to joke sometimes (even with units), but it should be clear that this is not serious :



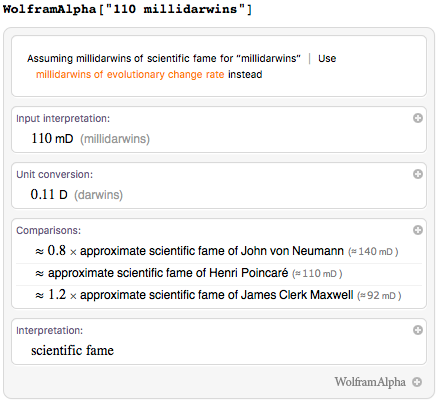
There are still obviously unscientific units, such as “helens” for beauty, “puppies” for happiness or “darwins” for glory:







I am very proud that SI units are not dead paper symbols, but tools that govern the modern world. Although I am not a fan of comics, I liked the recent presentation of basic units in the form of superheroes from the National Institute of Standards and Technology (NIST):





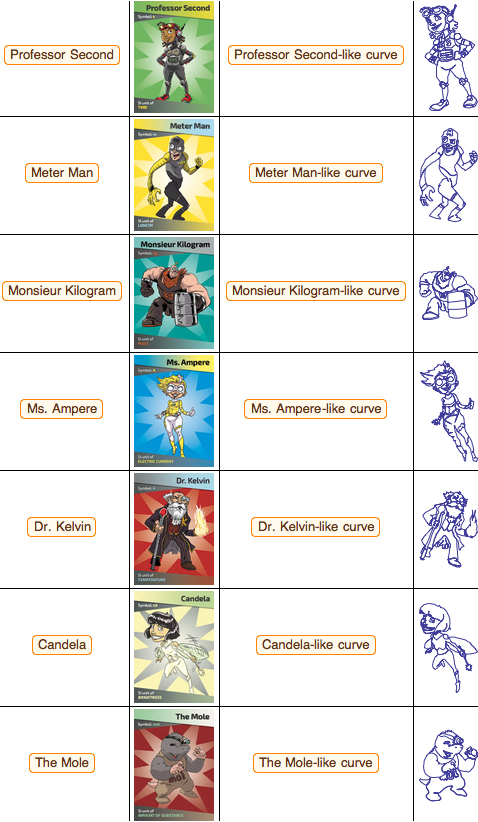
Please note: in order to honor the contribution of five great mathematicians to the creation of the metric system, the curves in the far right column are given as mathematical formulas; for example, for Dr. Kelvin we have the following purely trigonometric parameterization:



Thus, we can “build” Dr. Kelvin:



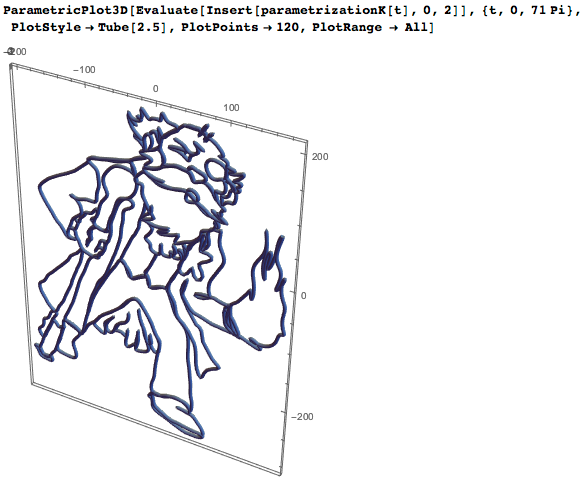
The presence of such characters in a parametric form is very convenient: when my family gets together, the kids do their favorite thing: they paint superheroes. I just print out the curves and then the kids can have fun (I borrowed this idea a couple of years ago from the NCSA coloring book ). And whenever a new episode comes out, everyone gets together to watch it. As you know, the last episode is our favorite. Rumor has it that the upcoming book Return of Metrologists (2018 - will be an ideal year!) Supplements the existing book . I am glad that the importance of measurements and the basic metric system is celebrated on World Metrology Day - May 20.







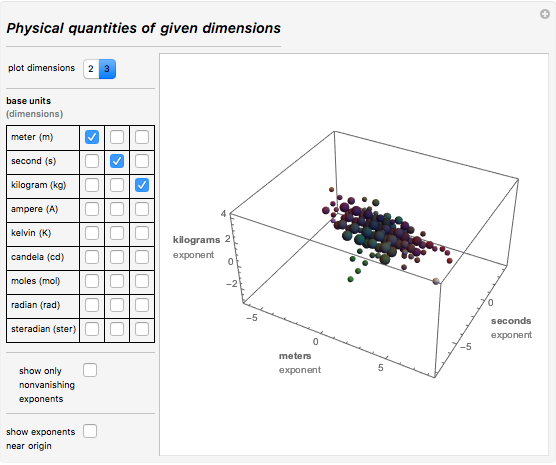
At the time I lived, people measured only goods: grain, potatoes and other products, as well as wine, fabrics, firewood, etc. So my country really needed units of length, area, volume, and, of course, units of time. I always knew that the importance of measurements will only grow over time. It is noteworthy that only 200 years after I entered the celestial spheres, the number of measured physical quantities reached several hundred. To date, only the International Organization for Standardization (ISO) defines and describeswhat physical quantities should be used. Below is an image of an interactive demonstration (download the document at the top of this post to interact with it), which graphically shows the dimensions of physical quantities for subsets of selected units. First select two or three dimensions (basic units). Then the graph will show the spheres with sizes proportional to the number of different units of measurement that are obtained from the selected ones. For example, in the case of “meter”, “second” and “kilogram”, the diagram shows such units of measurement of physical quantities as momentum (kg ¹ m ¹ s ^-1 ) or energy (kg ² m ¹ s ^-2 ):



Here is a snippet of the code that I used to create these graphs. These are all physical quantities with dimensions L ² M ¹ T ^-1 . The last one is a slightly exotic unit from electrodynamics :



Today, using smartphones, ordinary people measure a lot of physical quantities. I would say, "measurements rule." Or how my dear friend William Thomson used to say:

... When you can measure what you are talking about and put it in numbers, you know something about it; but when you cannot put it in numbers, your knowledge is scarce and unsatisfactory; it may be the beginning of knowledge, but, regardless of the subject, you are unlikely to have reached the stage of science.

Here is a graphical visualization of physical quantities that are measured using the most common measuring instruments:



Electrical and magnetic phenomena are only gaining popularity. Electromagnetic effects associated with physical quantities became popular much later:





I still remember how excited I was when in the second half of the nineteenth century and at the beginning of the twentieth century various physical quantities of electromagnetism were discovered and their relationship was understood (and do not forget about the recent addition memristor ). Below is a diagram showing the most important electrical / magnetic physical quantities q _k , which have relations of the form q _k = q _i q _j:



On the other hand, I was sure that the phenomena associated with temperature would soon be fully understood. And indeed: just 25 years later, Carnot proved that heat and mechanical work are equivalent. Now I also know about time dilation and length reduction according to Einstein's theory . However mankind still unknown whether the moving body more cold or warmer than a fixed (or they have the same temperature ). Every week I hear from Willard Gibbs about the related topic of freezing temperatures.. And recently, he was very excited about the news that the maximum temperature value for a given volume V is expressed through fundamental constants : The



maximum temperature of one cubic centimeter:

The increase in the number of constants

After a long time after my physical death, the best scientists in the field of physics of the 19th and early 20th centuries. - James Maxwell , George Stoney and Max Planck (and Gilbert Lewis ) discussed units of measurement of time, length and mass, based on the invariable properties of microparticles and associated with fundamental physical constants (speed of light, gravitational constant, electron charge, Planck constant, etc. .):



Maxwell wrote in 1870:

Nevertheless, the size of our Earth and the time of its rotation are characterized by enviable constancy. The earth may shrink, cool, or expand due to a layer of meteorites falling on it, or its rotation speed may weaken - and yet it will be the same planet as before.

But a molecule of, say, hydrogen, if its mass or the time of its vibration change at least a little, will no longer be a hydrogen molecule.

So, if we want to get standards of length, time and mass, which should be absolutely constant, we must look for them not in size, or in motion, or in the mass of our planet, but in the wavelength, period of vibration, and in the absolute mass of these imperishable, unchanging and completely similar molecules.

When we see that here, as in the starry sky, there are innumerable small bodies of the same mass, not further separated and vibrating simultaneously many times per second, and when we reflect on the fact that no force in nature can now change mass or the period of any of them - then we seem to have moved along the path of natural knowledge to one of those points at which we must take that faith, thanks to which we understand what everything visible consists of.

At the time when Maxwell wrote this, I was already in heaven for a long time, and when I read this, I applauded him (let me still have some skepticism regarding all the ideas coming from Great Britain). I knew that this was a way forward, allowing us to perpetuate the units that we created during the French Revolution.

There are many physical constants. And not all of them are known with equal accuracy . Here are some examples:



Converting the value of constants with a known error into arbitrary precision numbers is convenient for the following calculations. The relationship between confidence intervals and the number of digits is defined as follows: a number of arbitrary accuracy that corresponds to v ± δ is a number v with an accuracy of -log ₁₀(2δ / v ). And vice versa: if a number is given with arbitrary accuracy, we can recreate v ± δ:



After well-defined constants, the Rydberg constant with its 11th decimal places is distinguished from other constants by its accuracy. At the other end of the spectrum is G - the gravitational constant. At least once a month, Henry Cavendish stops with my next idea on how to build a bench-top device for measuring G. Sometimes his ideas are based on cold atoms, and sometimes superconductors. If he could still communicate with the living, he would write weekly comments in Nature. A little over a year ago, Henry was worried about the need to take his measurements in the winter, but later he found out that there is no seasonal dependence on the G value . The preliminary deadline for the Big G Challenge was just four days ago. I think that next week I will look from heaven at preliminary experiments.

There are other physical constants. Some of them are more fundamental than others, but now I do not want to go into a detailed discussion of this topic. The interested reader will like the articles of Levi Leblond (and here's another ), and this article , and this one , and the already classic articleDuffa Perch-Venice . To create units of measure based on physical constants, the differences between the classes of physical constants are not so relevant.

The absolute values ​​of the constants and their relation to Paradise, Hell and Earth are a separate issue. This topic is being vigorously discussed by mortals (also see this article ). Some numerical coincidences (?) Are simply perplexing:



Of course, using modern mathematical algorithms like lattice reduction, we can do numerology on the numerical part of physical constants:



For example, how can we derive the number π based on fundamental constants?



Or let's look at my favorite number, say 10 - the mathematical basis of the metric system:



Given the available set of constants, there are many ways to derive a unit of measure from a given unit. Today there are so many physical constants that you should really be interested in them, so as not to get lost in this set. Here are some of the least known constants:



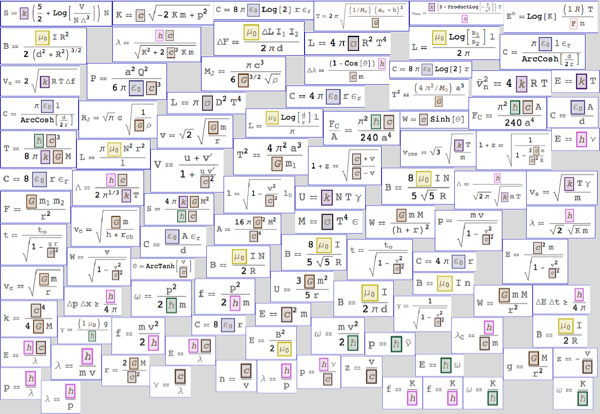
Physical constants appear in many equations of modern physics. Here is a selection of 100 simple physical formulas containing fundamental constants:



Of course, more complex formulas also contain physical constants. For example, in the formula of gravitational potentials of various objects, the gravitational constant (of course!) Of various objects appears, for example, for the segment potential and triangle potential:



My friend Maurits Cornelis Escherloves such formulas. He recently showed me variations of several of his 3D paintings, which show the equipotential surfaces of all objects in images by triangulating the entire surface, and then apply the above formula. The graph shows a stripped-down version of two equipotential surfaces:



I often stayed with Maurits Cornelis, and almost always he was in the company - usually Albrecht Durer . They are both lovers of playing with shapes, surfaces, and polyhedra. They deform them, invert and much more. Albrecht also likes to apply the smoothing technique with respect to gravitational potentials, but often does this only from the edges. Here is what Dürer equipotential surfaces of solids look like:



And here is a visualization of formulas containingwith ^α –h ^β -G ^γ in the space of degrees αγβγγ. The size of the spheres is proportional to the number of formulas containing with ^α · h ^β · G ^γ ; moving the cursor over the spheres, you can see the actual formulas in the attached document. We consider positive and negative degrees the same way:



And here is one of my favorite formulas for quantum-corrected gravity , which contains three of my favorite constants: the speed of light, the gravitational constant and Planck's constant: The



formula for the entropy of a black hole is also one of my favorites. In addition to c, h and Git contains the Boltzmann constant:



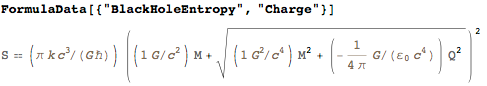
And, of course, the second-order correction to the speed of light in vacuum in the presence of an electric or magnetic field due to photon-photon scattering (without taking into account the polarization-dependent constant). Even in very large electric and magnetic fields, the changes in the speed of light are very small:



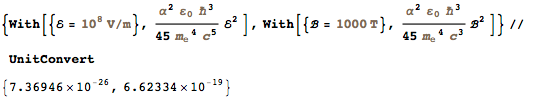
At the time in which I lived, we did not understand the physical world to such an extent that we came up with natural units. This continued until 1874, when Stony first introduced natural units of measure to the British Science Association in his lecture. Later, in his lectures of 1906-07, Planck already made extensive use of the units of measure (now called Planck units), already introduced by him in the famous article of 1900, " Annals of Physics". Unfortunately, in both of these unit systems the gravitational constant G takes a prominent place. Today we cannot measure it accurately enough. As a result, the values ​​of Planck units in SI have only about four decimal places:



These units were not suitable for daily use because it was either too small or too large compared to the lengths, areas, volumes and masses that people came across daily, but why not build units suitable for daily CSOs use, based on such constant microscopic properties?

(Note: The funny thing is that in the last 20 years, Max Planck again doubted that his constant hreally fundamental. He hoped that in 1900 he would get its meaning from semiclassical theory. Now he hopes to deduce it from some holographic arguments. Or at least he thinks determine the value of h / the k _{Bed and} . I don’t know if he will succeed, but who knows? He is a smart guy).

To date, many exact and approximate relationships between fundamental constants are known. Some may be discovered in the future. Can the Planck constant potentially be related to the size of the universe?



Here's another Beck formula showing a wonderful coincidence:



However, in my time no one could have thought of expressing the height of a giraffe using fundamental constants. Therefore, I was so amazed when, about 10 years ago, looking through new arXiv preprints, I found a formula for determining the height of the highest living creature that can run, obtained by don Page . He got the height of the giraffe (the brachiosaurus and zavroposeidon do not count, because they cannot run) in terms of fundamental constants with an error of no more than 2 times - I think this is simply amazing:



In 1983, Press, Lightman, Peierls and Gold expressed maximum human speed (see also earlier Press articles ):



I also really liked the work of Barrows and Ostraiker on expressing the sizes of various astronomical objects only through fundamental constants. For example, for the mass of a typical galaxy, we get the following expression:



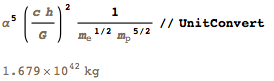
This value is within a small deviation from the mass of the Milky Way:



However, we will return to our units of measurement and quickly rewind time 100 years ahead, once in the second half of the 20th century: the idea of ​​basing units on The properties of microscopic objects became more and more widespread .

In 1967, the second was defined as the time equal to 9 192 631 770 periods of radiation corresponding to the transition between two ultrathin levels of the ground state of the cesium-133 atom at rest, and the meter in 1983 was defined as the distance that light travels in vacuum for a period of time equal to 1/299 792 458 seconds. To be precise, this definition must be implemented at rest, at a temperature of 0 K and at sea level. Neglect of sea level can lead to significant measurement errors; the Earth’s core is almost 2.5 years younger than its surface due to differences in gravitational potential .

Now the definitions of second and meter as units of measurement are really equal for all people. They are equal not only for people on Earth, but also in the future, and far, far from Earth for any alien (once the cesium periods are likely to be replaced by a large number of periods of another element, but this will not cancel the universality of this unit of measurement).

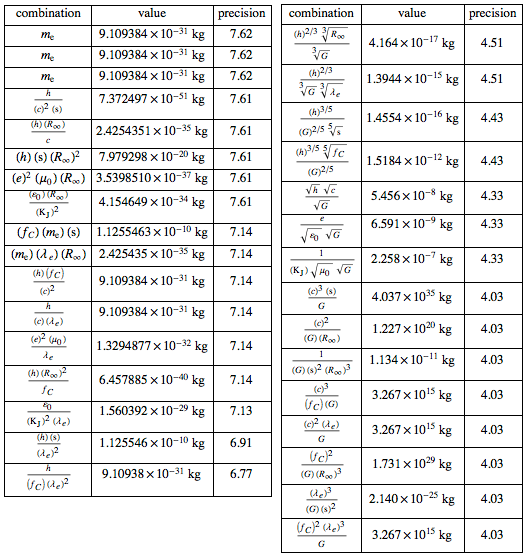
However, if we want to justify all units through physical constants, which ones should we choose? There are many ways to express the basic units of measurement through a set of constants. Using the constants from the above table, you can get thirty (thirty!) Ways to combine them to get a unit of mass:


Due to the different accuracy of the constants themselves, their combinations will also differ in terms of accuracy (and numerical values ​​too):



The question is, which constants should be chosen to determine the units of the metric system? Many aspects need to be considered: from accuracy and practicality to overall consistency. We want our formulas to look like F = m a , and not contain explicit numbers like the Thanksgiving turkey cooking time formula (suppose a spherical turkey):



Or in the PLANK formula for calculating engine power in horsepower:



Here, in the sky, we we cannot use physical computers, so I'm glad that I can use the virtual Wolfram Open Cloud for my calculations and experiments. I have been playing with interactive constant units (below) for many hours, and I completely agree with the choice made by the International Bureau of Weights and Measures(BIPM): speed of light, Planck constant, elementary charge, Avogadro number and Boltzmann constant. I showed a preliminary version of this article for Edgar's blog , and he was very glad to see this table, which is based on his old article :



I want to note that the most popular physical constant - a fine structure constant - is not very useful for building units. Given its dimensionlessness, it is clear why it cannot be associated with a unit of measure. Although, of course, this is one of the most important physical constants in our Universe (probably, it is surpassed only by a simple integer constant that describes how many spatial dimensions there are in our universe) Often various dimensionless combinations can be found from a given set of physical constants due to the relations between the constants: such as with ² = 1 / (ε ₀ μ ₀ ). Here are some examples:



Probably, there is no other constant that Paul Dirac and I would discuss in such detail over the past 32 years than the fine structure constant α = е ₂ / (4πε ₀ ħс ). And although we regularly meet with the Lord in a friendly and productive atmosphere, he still refuses to open the closed form α. And he won’t even tell us if he chose the same meaning for all times and places. As for the corresponding topic of the values ​​of the selected constants, he also refuses to discuss fine-tuning and alternative values . He says that one day we will all know. He outlined some boundaries, but they were not much more accurate than those that we know from discoveries on Earth. So, like living mortals, now we just have to guess the mathematical formulas:



Or combinations of constants :



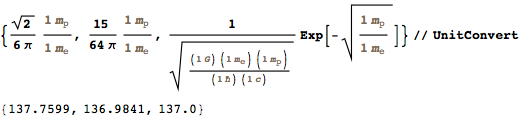
And here is one of my favorite coincidences:



And a few more :



The increasing importance and breadth of the use of physical constants is well reflected in the scientific literature. Here's a graph showing how often (number of publications per year) the most common constants appear in scientific publications from Springer . The logarithmic vertical axis shows the exponential growth of references to physical constants:



While fundamental constants are found everywhere in physics and chemistry, there are practically no references to them in newspapers, films, or advertising. I was very happy to see a new column called Measure for Measure in Nature magazine .



I hope that even before the redefinition, we will see new interesting video games that allow players to change the values ​​of C,G and h to see how the world around us changes depending on the values ​​of the constants. I really want to play such a game. With large values ​​of h, you can build a world with Schrodinger cats . And here with the help of the game you can introduce the constants of young children. This is exactly what Mr. Tompkins ' adventure game is :



It would be interesting to see how quickly and efficiently the human brain will adapt to possible life in another Universe. Initial studies are encouraging. But perhaps our world and our sky are really worked out in detail.

Existing SI system and kilogram problem

In addition to the meter and kilogram, other SI units are included in the modern SI. Ampere is defined as the force of a constant current passing through two parallel rectilinear conductors of infinite length, kelvin - through the thermodynamic temperature of a triple point of water, mole - through a kilogram and carbon-12, and candela - through the radiation of a completely black body. If you have never read the SI brochure , I highly recommend that you do so.

Two infinitely long wires - this, of course, is a macroscopic level. And to maintain the state of the triple point of water, a macroscopic amount is needed. This is not perfect, but normal. Carbon-12 is already a microscopic level. Radiation of a completely black body - again is an ensemble of micro-objects. Thus, some of the current SIs achieve, in a sense, Maxwell's goals.

However, the main reason for my insomnia over the past 50 years has become ... a kilogram. When I thought about him, my head started to hurt and nightmares tormented me.

In 1799 (this is also the year of my death) the first prototype of a kilogram was created - a small platinum cylinder. It was about 39.7 mm in height and 39.4 mm in diameter, and for 75 years it served as a standard kilogram. It was created from a forged platinum sponge made by Janeti. Miller gives many details of this kilogram sample. They are now in the national archives . In 1879, Johnson Matthey , using new melting techniques, made material for three new kilogram standards. Due to the slightly higher density, these kilograms were slightly smaller (39.14 mm lower). The cylinder was named KIII and became the new international kilogram prototype.. Here is the last sentence from the definition of the international prototype of the kilogram of 1885:



Several kilogram standards were selectively compared with our original standard; if you are interested in measurement details, see this book . All three samples were less than 1 mg lighter than the original kilogram. In one sample, the difference was less than 0.01 mg compared to the original kilogram. For a detailed history of creationsee Quinn. And still, by definition, a kilogram is the mass of a small metal cylinder lying in a safe of the International Bureau of Weights and Measures near Paris (although technically it is not located in France). He lies in a safe, which opens with three keys, under three glass domes - a small platinum-iridium cylinder that determines what a kilogram is. To orient you in geography, here is a map of Paris with the current standard of kilogram (in the south-west), our original (in the north-east), both in a yellow frame, and some other sights of Paris: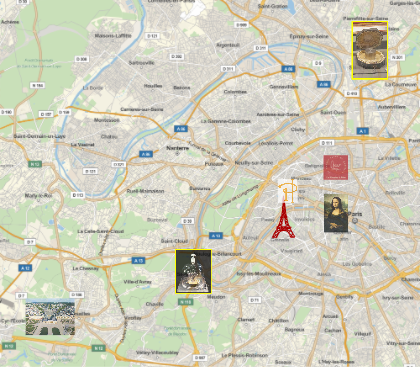



This kilogram standard, which made me unhappy, is very difficult to access. Every few years, a small group of people re-measures its weight (mass). And, of course, the result, according to the definition and the agreement concluded at the first General Conference on Weights and Measures in 1889, is equal to one kilogram.

Years later, the first kilogram standard received dozens of brothers and sisters in the form of national standards of other countries (of the same size, material and weight, accurate to a few micrograms, which are carefully recorded). It is a pity that the Internet was not invented before, because in that case I would have a communication channel to say what happened to the stolen Argentinean standard 45; after that he was re-melted. Immediately after creation, they had the same size and weight. It could be assumed that the weight of these cylinders would be stable. However, history has judged otherwise. Repeated measurements showed that almost all standards became harder every year . Or, more likely, this international prototype has become increasingly easy.

For many of these comparisons, I watched with great interest in my heaven. Comparison of their masses represented significant difficulties. First, national prototypes must first be delivered to Paris. I silently listened to lengthy discussions with TSA members when a metrologist arrived with a platinum kilogram, materials for which cost about $ 50,000 (you need to add another $ 20,000 for manufacturing), which was lying in a shiny golden container and which should only be opened in a clean room with gloves on and with a mouthpiece in his mouth, so that he would never be touched by a human hand), and explained all this to TSA members (an official letter is in this case a great help). What I watched here was even funnier than the scenes from the 1001 gram film .

Then comes the complicated cleaning procedure with hot water, alcohol and UV radiation. All samples lose weight in this process. Then they are all carefully compared to each other. And as a result, all this with a high degree of probability leads to the fact that my favorite international standard kilogram loses weight. This fact robs me of sleep.

Here are the results of the third verification (from 1988 to 1992). The figure shows the difference in weight compared to the international prototype:



To find out about measurements taken over the past two years, see this article .

When I say that a kilogram “loses weight”, I mean the following. By definition (independent of its “real objective” mass), the international standard has a mass of exactly 1 kg. Compared to this mass, most of the other kilogram standards seem to be gaining weight. Since other standards were created gradually over more than 100 years using various methods, it is very likely that the international standard becomes easier over time (this is not due to the greed of Ceausescu who steals platinum; the Romanian prototype was already at 953 mcg in 1889 lighter than the international kilogram standard).

Willard Gibbs, my old friend, often says that his pound still uses a pound, not a kilogram. His voice in the election this year will clearly be for Bernie. At least a pound is a certain fraction of a kilogram, so everything that happens with a kilogram will affect the pound in the same way:

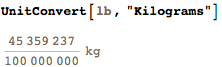
New SI

But soon all my dreams and centuries-old hopes will come true, and again I can fall asleep. In 2018, that is, only two years later, the most grandiose (starting with my work with Laplace) changes in the history of units and measurements will occur.

All units of measure will be based on things that are accessible to everyone and everywhere (meaning access to some modern physical instruments and devices).

Below, on Earth, they began to be called " reference constants ."

Some people also call the new SI “quantum SI” because of its dependence on the Planck constant and elementary charge e . In addition to the importance of the Planck constant ( h ), with h and ein quantum mechanics, the following quantum effects are related: the Josephson effect and the associated Josephson constant K _j = 2 е / h , as well as the quantum Hall effect with the Klitzing constant R _K = h / е ^2. Quantum metrological triangle: connecting frequency and electric current by tunneling of single electrons, connection frequency and voltage across the Josephson effect and the voltage connection and an electrical current through the quantum Hall effect would be an excellent implementation of electrical quantities (after many many years, so noted Enin , we have to worry about the effects of QED second order , but it will not be soon).

BIMP already has a new logo for the future International System of Units:



Specifically, the proposal is as follows:

1. The second will still be determined through the microwave radiation of the cesium atom.
2. The meter will still be determined through a precisely defined speed of light.
3. A kilogram will be determined through the exact value of the Planck constant.
4. Ampere will be determined through a precisely defined value of the elementary charge.
5. Kelvin will be determined through a precisely defined value of the Boltzmann constant.
6. The mole will be determined through the exact (calculated) value.
7. The candela will be determined by the exact value of the candela ratio of the steradian-per-watt at a fixed frequency (already now used in some cases).

I highly recommend you read the new SI draft brochure . Laplace and I talked a lot about her, and we liked her. Here is a word cloud from the new SI brochure: I have



n’t forgotten yet: below are some comments regarding other units.

Second

I still remember when we discussed the introduction of metric time in the 1790s: a 10-hour day, 100 minutes in an hour, and 100 seconds in a minute. Looking back, I understand that this was not such a good idea. People’s habits are sometimes too hard to change. And I'm so glad that in recent years I was able to interest Albert Einstein in metrology. We talked a lot about the meaning of time and the difference between measured local and coordinate time. But we will not talk about this today. The uncertainty of a second today is less than 10 ^-16 . Maybe one day cesium will be replaced with aluminum or another element to reduce the uncertainty by 100 or even 1000 times. But this does not change the spirit of the new SI; we are talking about small technical changes (if you are interested in the details, seethis article ).

Obviously, today's definition of a second is much better than the previous one. At a time when prices in the stock market are compared at the level of microseconds, the change in the length of the day due to earthquakes, melting glaciers, drift of continents and other phenomena that have been occurring for more than a hundred years is quite large:

Mole

I heard that some chemists complain that the moth (their favorite unit introduced in SI only in 1971) will be vulgarized. In the currently used SI mole, it is determined through the number of atoms in carbon-12. In the new SI, it will simply be about counting objects — the true chemical equivalent of a damn dozen. Based on the Avogadro number, the mole plays an important role in combining the microworld with the macrocosm. A more mundane definition of a mole depends on a given quantitative value - for example, on the pH value. Second - the base unit of time in SI; mole is the basic unit of a physical quantity or quantity of a substance :



However, not everyone likes the term " quantity of substance ". Even this year (2016), alternative names were proposed: for example,stoichiometric amount . Over the past decades, it has been proposed to replace the entire variety of names with the phrase “quantity of substance”. Here are some examples :



But in SI, only the name of the unit of measurement is defined - “mole”. The naming of a physical quantity, which is measured in moles, remains to the International Union of Theoretical and Applied Chemistry .

To see the latest discussions this year, see Leonard’s article : “ Why is the“ amount of substance ”so poorly understood? The mysterious Avogadro is to blame! ”

But what if we could create an “ideal cube” that would represent the Avogadro number? That would be easy to conceptualize.Such an option was proposed several years ago - an option compatible with the value of the Avogadro constant (as a result, a cube with an edge length of 84,446,888 elements would be obtained). During a game of heavenly cricket, I asked Srinivas Ramanujan and Harold Hardy , his long-time friend, what was special about 84,446,888, but so far they had not come up with anything deep. He said that 84446888 = 2 ³ * 17 * 620933, and the number 620 933 appears starting from the position 1,031,622 decimal digits of the number π, but I personally do not see anything related to metrology in this.

Here is the latest CODATA (Committee on Data for Science and Technology) fromlist of constants, units of measurement and uncertainties of the National Institute of Standards and Technology :



The above cube is too small.



Interestingly, if we agreed on the option of a body-centered lattice with one additional atom in a unit cell, we could still adhere to the interpretation of the cube:



A face-centered lattice would not work:



But a diamond (silicon) lattice would be:



Summarize:



Here's another one little thing:

In the midst of the Cold War, the accepted value of the Avogadro number changed in the third sign. This was a major change, given that a protracted debate is currently underway regarding disagreements regarding the sixth category. Can you explain the sudden decrease in Avogadro's number during the Cold War?

Do you know the answer? If not, look here or here .

However, I moved away from the main idea. Since I am more interested in units of measurement of mechanical quantities, I will leave my old friend Antoine Lavoisier to judge the new definition of a mole, since he was the chemist in our team.

Kelvin

Willard Gibbs convinced me that temperature should be determined mechanically. I'm still trying to understand what John von Neumann is thinking about this (since I never fully understood his evening lectures on factors of type II and type III, my opinion about Kelvin never came to be). Different temperatures correspond to nonequivalent representations of algebras. I did not think about how best to define kelvin from the point of view of algebraic quantum field theory. I asked John about his opinion on the first-principle h / k estimate based on the Tomita-Takesaki theory, and even he was not sure about that. He told me something about the thermal time and temperature of the diamond, but I didn’t understand much of this.

And then we have the opportunity to get the value of the Boltzmann constant. Even 40 years after the publication of the Koppe-Huber article , it is unclear whether this is possible. I have already thought about this, and I take into account the various options . As I said, it is not clear to me how to determine the value of temperature and the unit of its measurement. I have no doubt that the new definition of kelvin will be a big step forward; But is it the last one?

Ampere

This is one of the most direct, intuitive and beautiful definitions in the new SI: current is just a certain number of current electrons (per second). Determining the value of ampere through the number of elementary charges is simply brilliant. When it was first proposed, Robert Millikan was so happy that he invited many of us to meet in the afternoon in the courtyard of his house. Both in theory and in practice, when measuring the electric current of electrons in crystalline objects, we must remember that electrons are quasiparticles. However, since 1959, thanks to Walter Cohn, we know that we should not expect that the charge of an electron in a crystal will be the same as the charge of a bare electron. Since the elementary charge is a rather small charge, the question of measuring fractional charges is not relevant now. Personally, I believe that Robert's contribution to the determination of physical constants at the beginning of the 20th century is clearly underestimated (Robert Andrews always knew what he was doing ).

Candela

Does this unit deserve to be among the main ones? The whole history of human-centered physiological units is rather confusing. Obviously, they are extremely useful. We all see and hear every day, every second. But what if the human race continues to evolve (in the context of Darwin's ideas)? How will this fit our mantra “all the time”? I have some thoughts on this subject, but putting them here and now would mean taking the narrative away from the main topic for discussion.

Why are the basic units of measurement exactly 7?

I want to note that at first I was very concerned about the introduction of some additional units used today. In the course of endless discussions, Gauss (my chess partner) managed to convince me that we can reduce all measurements of electrical quantities to measurements of mechanical properties, so that in the end I began to understand quite well the GHS system, which at first I did not like. However, the system of units of measurement created by man should be as useful as possible, and if these seven units perform their functions better than all, then they should be seven. In principle, you can even exclude the unit of mass and express the mass in time and length. However, besides being impractical, I am sure that this approach is conceptually wrong. I recently discussed this issue with Karl Friedrich. He said that in the late 1820s. there was an idea to just use time and length, but this approach was later abandoned. During his lifetime, Gauss did not have the opportunity to discuss the concept of mass with Kant , but over the past century they have agreed on mass as a priori (at least in this universe).

The motto for the original metric system was the phrase: "for all people, for all time." The current SI is already implementing the first part of the motto - “for all people”, and taking into account future changes, the second part will soon become a reality. You cannot imagine what this means to me. Fundamental constants seem to vary as much as possibleby an amount equal to about 10 ^-18 per year. This is many orders of magnitude farther from what is currently available for most precision units.

Of course, in the new SI, some values ​​will be more cumbersome. If we consider the current CODATA values ​​as accurate, then, for example, the von Klitzing constant e ² / h will turn out to be quite voluminous: The



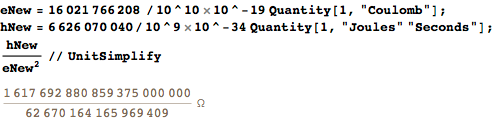
whole part of the last result is, of course, 25.812Ω. However, is it a periodic decimal or final decimal? Simple factors of the denominator tell us about the frequency:



Progress is good, but, as often happens, it also has a price. While the new definitions of SI units are beautiful, it becomes more difficult to understand them, and physics and chemistry teachers will need to come up with ways to explain these new definitions to students (to learn about the first attempts, see this and this article ).

And how many times have I met textbooks in which the magnetic permeability (vacuum permeability) μ ₀ was 4π10 ^-7 N / A ² ? Magnetic and electrical constants will become measurable in the new SI. Current exact value:



Given the Planck constant h and the elementary charge e, the value μ ₀will bear the uncertainty of the fine structure constant α . Fortunately, the dimensionless constant of the fine structure α is one of the most famous constants:



So what? Publishing houses of educational literature do not object to such an occasion for the reprinting of all their books. This is generally a great reason to sell more new books.

Given that μ ₀ will become a measurable quantity in the future, I predict a much greater use of an outsider among the fundamental constants - the vacuum impedance Z of the vacuum - in the future:



I applaud all physicists and metrologists for the hard work they have done over the past 225 years, the crown of which has become new definitions based on physical constants. So, my dear first committee members, these definitions are beautiful and timeless.

I know this is a bit immodest, but Joseph Louis Lagrange told me that he regrets that we did not introduce the basic and derivative units back in the 1790s. Now that the Planck constant is very important for the new SI, he thinks that we had to have a nominal base unit of measure for the action. And also, what you need then to make the mass a derivative. Despite the fact that this could become the aerobatics of classical mechanics, he nevertheless understands that the unit of measure for action would not become popular among farmers and peasants as an everyday unit of measurement.

I don’t have time to go into a detailed discussion of Bridgman’s quarterly garden festivals. I try to participate in each of them, if the schedule allows. Such events make us listen to the general discussion about the advantages and disadvantages of alternative systems of units of measure. As expected, Julius Vallot , Jan de Boer , Edward Guggenheim , William Stroud, Giovanni Georgi , Otto Hölder , Rudolf Fleischmann , Ulrich Stillet , Hassler Whitney and Chester Page were the most talkative at these parties. The discussion about the consistency and completeness of the system of units of measurement and what a physical quantity is is continued further. A recent discussion of whether probability is a physical quantitylasted for six hours, and in the end, no solution was found. The next time I suggested inviting Richard von Mises and Reichenbach - they would definitely offer something worthwhile. Otto always complains at parties that mathematicians are no longer interested, as before , in the topic of units of measurement and systems of units of measure, and that he is very happy to see that recently theoretical physicists have been raising this topic from time to time: see the vector differentiation of physical units or a recent article on the general structure of unit systems . And when he saw in the article about the proceedings in Dagstulthat a new type of theory combines units of measurement and physical quantities, he was extremely excited.

It is interesting to note that roughly the same discussions took place three years ago (and have since been regularly organized) during the monthly mountain walks organized by Claude Shannon . Sylard argues that the “bit” should become the basic unit of SI in the future. In his opinion, information as a physical quantity is greatly underestimated.

I repeat again: the new SI will be just wonderful! However, I would like to change a few details. Here is the current status of radians and steradians that are in SP 811defined as derived units: "Radian and steradian are special names for one that can be used to convey quantity information." However, I can not but note that experts discuss this topic in detail .

In honor of the new SI, we raised funds to celebrate this event. We gathered enough to hire Michelangelo . He will do the sculpture. The sketches presented to the Committee (I was lucky to have an honorary chairmanship) are intriguing. I'm sure she will compete with David himself. Each person will one day be able to see her (it depends on your current age and bad habits). In addition to constants and units proper, he also plans to create sculptures of Planck, Boltzmann and Avogadro, since constants are named after them. And if Max could pose right away, then in order to get permission for Boltzmann to leave hell for a while, problems arose (Milliken and Fletcher were, for obvious reasons, a little disappointed). Oddly enough, it was Paul Adrien Maurice Dirac who invented how to convince Lucifer to let go of Boltzmann. The irony is that Paul himself was not so keen on the new SI due to the fact that the constants themselves depended on time for billions of years. In any case, Paul noted that there are three fundamental constants: Planck's constant (6.62 ... × 10 ³⁴J · s), the Avogadro number (6.02 ... × 10 ²³ / mol), and the gravitational constant (6.6 ... × 10 ^-11 m ³ / (kg · s)) all begin with the number 6. The fact that all three fundamental constants form the number of the beast, impressed Lucifer, so it can be expected that he will approve a temporary vacation for Ludwig.

As a former sailor, I also pointed out to Lucifer that the average depth of the ocean is exactly 66% of its height (2443 m, according to a detailed reanalysis of Dante’s Divine Comedy ). He so loved this sweet fact that now he owes me.



Until now, Lucifer insists on the combination of G (m _e / (hk)) ^1/2for sculpture. The reason is obvious:


Let's see how the discussion unfolds. There really is nothing wrong with this combination (even if it does not physically make sense), so that we could agree with his requirements.

An agreement has also been reached on music: we will play Sinfonia de motu Wojciech Kilar , who presented physical constants as a musical composition, using only notes C, G, E, H (B flat in English-speaking countries), and A (which represents cesium atom). And we want to convince Rilke to write poetry in honor of this event.

Below, on Earth, the appearance of constant-based units of measure will also be noted. I look forward to a documentaryThe status of the unit of measurement about the history of the kilogram and its redefinition through the Planck constant.

The way to change the definition of a kilogram

I have already mentioned that the most important innovation of the new SI will be a modified definition of a kilogram. After all, the kilogram present in the current version of SI is an artifact. In addition, many other derived units depend on it: say, volts. Changing the definition of a kilogram will make many electricians happy.



The resulting value for the Klitzing constant and the Josephson constant is very close to the last CODATA value of the Planck constant : A



kilogram is the basic SI unit for the amount of mass. Mass is most relevant to mechanics. Thanks to Newton’s second law, 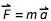mass is closely related to force. Suppose we understand length and time (and therefore acceleration). What's next? William Francis Maggie wrote in 1912:

It would be inappropriate to dogmatize, and, accordingly, I should crave forgiveness for the fact that I often express my opinion, believing that it is less reprehensible to be selfish than dogmatic ... The first question that I will consider is raised by proponents of a dynamic definition of strength and is in what order the ideas of the concepts of force and mass appear; in other words, which of the concepts is primary ... He [Newton] proposes mass as a fundamental quantity, which is necessary for establishing a dynamic measurement of force ... I cannot find any definition of mass at Lagrange ... In order to measure mass, we must start with intuitive knowledge of the force, and then use it in experiments with which we first determine and then measure the mass ... Now, thanks to the constancy of the mass of matter,

Henri Poincare in his book Science and Method writes:

Knowing the strength, it is easy to determine the mass; this time the definition should be borrowed from the dynamics; there is no way to do it differently, as a result we should get an idea of ​​the difference between mass and weight. Here, again, experiments should lead to the definition.

I always had an intuitive understanding of the meaning of mass in mechanics, although until the middle of the twentieth century I was never able to express it clearly. Only recently, with the help of Valentin Bergman and Jean-Marie Surio, did I fully understand the role of mass in mechanics: mass is an element of the second cohomological group of the Lie algebra of the Galileo group .

Mass as a physical quantity manifests itself in various fields of physics. In classical mechanics, it is associated with dynamics, in the general theory of relativity, with the curvature of space, and in quantum field theory, mass appears as one of the Casimir operators of the Poincare group.

In our weekly seminar Philosophy of Physics, which this year was led by Immanuel,Hans Reichenbach and Karl Friedrich von Weizsacker (it was Pasqual Jordan who suggested that the three men lead the seminar), we have been discussing the nature of the mass for 5 meetings. The topics for this year's seminars were the rules of mass super-selection in nonrelativistic and relativistic theories, the concepts and use of negative mass, the uncertainty of mass-time relations, non-Higgs mechanisms of mass production and scaling in biology and sports. I need at least three days of preparation for each of the seminars, and the list of books recommended for reading is more than nine pages (which emphasizes how many condensed matter phenomena exist) I look forward to this year, dedicated to the mass; and I’m sure I will understand a lot. I hope that Ehrenfest , Pauli and Landau will not constantly interrupt the speakers, as they did last year (the conversation about the mass in the general theory of relativity was especially unsuccessful in this sense). In the last seminar of this series I will have to make a speech. As for the laws of scaling, my favorite example is as follows:



I am also going to talk about the recently found power law of a predator-victim .

As for sports, I already have a good example that I was inspired by Texier et al.: ratio between the mass of a sports ball and its maximum speed. The following diagram allows me to assume that speed _max ~ ln ( mass ). Move your mouse to see the ball’s mass and maximum speed (in the attached document) ::



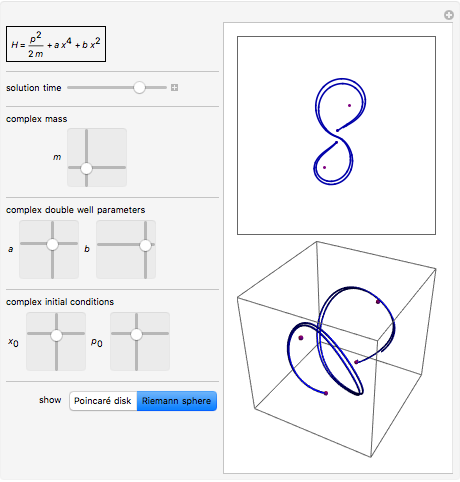
For the negative mass workshop, we had some interesting homework: visualizing the trajectory of a classical point particle with a complex mass (double-hole potential). Since I saw some of Bender's work on the trajectories of complex energy, those trajectories that I received for complex masses did not surprise me:



Recent remarks.

The whole new definition is:

a kilogram is a unit of mass; its value is established by fixing the numerical value of the Planck constant equal to exactly 6.62606X * 10 ^-34 , when it is expressed in units of s ^-1 · m ² · kg, equivalent to J · s. Here X denotes some numbers representing the latest experimental values.

A kilogram cylinder can finally resign as the most precious artifact in the world. I expect that soon after this event, the international standard kilogram will finally be in the Louvre. As soon as the Louvre was declared a “ place for the unification of monuments of all sciences and arts ” in May 1791, and then opened in 1793, all committee members agreed that one fine day, when the original kilogram standard would be replaced by then another, he will move to the Louvre. This standard has earned its place. I even bet that within a few years a retired standard under three glass domes will become one of the most popular objects of the Louvre. And the queue that is formed in front of him of physicists, chemists, mathematicians, engineers and metrologists will be longer than the queue for the Mona Lisa. I would also like to bet that in a few years beautiful miniature replicas of a kilogram will become the best-selling product in the store at the Louvre:



At the same time, maybe it’s worth leaving the standard where it is now, for another 50 years, to measure it and compare with a standard made on the basis of the exact value of the Planck constant. Then, finally, we will find out for sure whether the international prototype of the kilogram lost weight.

Let me quickly repeat all the steps that led us to a new, “ electronic ” kilogram .

One could define a kilogram through the Avogadro number as a certain number of atoms, say ¹²C. But because of the binding energy and surface effects occurring in carbon (diamond or graphene) made up of n = round (1 kg / m ( ¹² C)) atoms so that a mass of 1 kilogram is obtained, all n carbon atoms -12 should be well separated. Otherwise, we would get a mass defect (remember the famous Albert formula E = m c ² ), and the mass of the equivalent of one kilogram or mass of carbon compared to the same number of separate, well separated atoms would be about 10 ^-10 . Using the energy of the carbon-carbon bond, we estimate the mass differences:



The mass difference with this size and weight of 1 kg can beeasily detected using a modern mass comparator .

To convey the scale: this would be equivalent to the relativistic transformation of mass (Einstein's) from the expenditure of energy on fencing all day:



This does not mean that it is impossible to determine a kilogram through the mass of an atom or its part. Given that the mass of the carbon atom is m ( ¹² C ), the atomic unit of mass is u = m ( ¹² C ) / 12; therefore, with u, you can easily go to the Planck constant:



I read with great interest the last comparison of using different sets of constants to determine a kilogram. Of course, if the mass of the carbon-12 atom has a certain value, then the Planck constant will become measurable. It seems to me that it is aesthetically more preferable to have the exact value of the Planck constant.

I carefully watched what was done in the last decade to redefine the kilogram. The events of the past 20 years suggest that the kilogram will soon fall from the pedestal.

And when 11 years ago I read an article by Ian Mills, Peter More, Terry Quinn, Barry Taylor and Edwin Williams entitled “ Redefining a Kilo: A Decision That Has Come ” in Metrologia (this magazine is in my list of favorites in second place after the daily New receiptsco-published by Hells' Press, publishing group Heaven, Jannah Media and Deva University Press), I already knew that my dreams would come true soon. At that moment when I read Appendix A.1 Definitions that fix the value of the Planck constant h , I knew what would happen next. Although the idea itself was in the air much longer, now it has taken shape in a real program, which will be implemented within ten years.

James Clerk Maxwell wrote in his Treatise on Electricity and Magnetism of 1873:

In developing a universal system of units, we can derive a unit of mass from already defined lengths and times, and, given the current state of science, we can only do this in a rough approximation; if we expect that in the near future we will be able to determine the mass of one molecule of a standard substance, we can wait for this definition to fix the universal mass standard.

Until about 2005, James Clerk believed that mass should be determined through the mass of an atom, but then he changed his mind and currently stands for determination based on the Planck constant.

In a conversation with Albert Einstein and Max Planck (it seems that it was in the early seventies) in a Viennese-style coffee house (Max loves Sacher cake and was happy when Franz and Eduard Sacher opened their now famous HHS (“Heaven Hotel Sacher”), Albert proposed using his two famous equations: E = mc ² and E = hf to search for m to get m = hf / s² . Thus, if we define h , as was done with s, then we find out m ( Compton claimed that this equation was simply rewritten, and Niels Bohr noted that we cannot trust E = mc ² because of its relatively weak experimental verification, but I think he’s just mocking Einstein - he’s avenging some Solvay conference on the discussion of thought experiments, and, of course, Bohr could not resist Δm Δt ~ h / s ²as the reason why we cannot determine the second and kilogram independently of each other, since an error in one implies an error in the other for any finite mass measurement time. But Rosenfeld convinced Bohr that this was still a long way off, since the accuracy of measuring mass is about 10 ^-52 kg for a mass m of 1 kg.).

The frequency equivalent, corresponding to f = m with ² / h , is not practical for a kilogram of mass, since this will mean that f ~ 1.35 × 10 ⁵⁰ Hz, and this is too large for any experiment. However experimentsconducted in Berkeley in recent years, perhaps, will allow the use of such methods on a microscopic scale. For more than 25 years, at every meeting of the NSF (Heavenly Physical Society), Louis de Broglie has insisted that these frequencies are real physical processes, and not just convenient mathematical tools.

Therefore, we must know the value of the Planck constant h . Until now, a kilogram is defined as the mass of its standard. As a result, we can measure the value of h using the current definition of a kilogram. After we know the value of h with an accuracy of about 10 ^-8 , we can determine the specific value of h. From that moment, the kilogram will be implicitly determined through the value of the Planck constant. During the transition, these two definitions will overlap in their uncertainty, and no gaps for any derived quantities will arise. International prototype over the past 100 years, has lost about 50 μ g of body weight (relative change of 5 × 10 ^-8 ), so the value of Planck's constant with an error of less than 2 × 10 ^-8 ensures that the mass objects is not significantly changed.

Over the past 116 years, the value of the Planck constant has become more accurate by 7 digits. A real success! In his article “ On the law of energy distribution in the normal spectrum, ” Max Planck first used the symbol h, and for the first time - the numerical value of the Planck constant (in an article published a few months ago, Max used the symbol b instead of h):



I asked Max why he chose the symbol h, and he replied that he did not remember. In any case, he said that it was a natural choice (as in the case of the symbol k for the Boltzmann constant). It can sometimes be read that the symbol h was used to express the German word Hilfsgrösse (auxiliary variable); Max said that perhaps it was, and that he really does not remember .

In 1919, Raymond Thayer Birge published the first detailed comparisondifferent measurements of the Planck constant:



The value of the Planck constant has changed from 6.55 × 10 ^-34 J · s to the 2016 value of 6.626070073 (94) × 10 ^-34 J · s: amazing progress .

The following interactive demonstration allows you to zoom in and out to see progress in measuring the Planck constant h over the last century. Hover over the Bell curves (showing the uncertainty of the values) in the document to see the experiment (for a detailed discussion of many experiments to determine h see this article ):



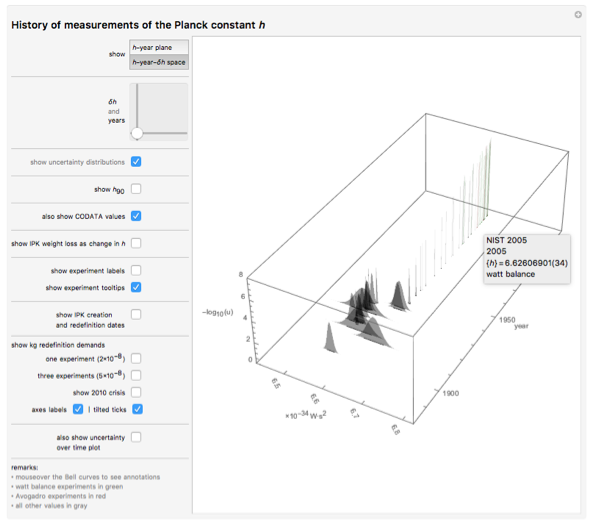
My group willingly watched from heaven two important experiments of recent years: the watt balance experiment and the Avogadro project. As a person who was engaged in mechanical measurements during his lifetime, I personally love the watt balance experiment. Building a mechanical device that, thanks to a cunning trick from Brian eliminates an unknown geometric dimension, is worthy of applause. The recent do-it-yourself LEGO home version was especially pleased . With a few hundred dollars invested, everyone can measure the Planck constant at home! The world has changed a lot since I lived in it. You can even check your memory card before you put the file there, and then to see if its mass has changed .

But my dear friend Lavoisier, as expected, always loved the Avogadro project , designed to determine the value of the Avogadro constant with high accuracy. Pure silicon (99.995%) makes the chemist's heart beat faster. The product of the Avogadro number with the Planck constant N _A h is related to the Rydberg constant. Fortunately, as we saw above, the Rydberg constant is determined with an accuracy of about 11 digits; this means that N _A h allows us to find the value of our favorite Planck constant hwith a high degree of accuracy. Even during my life, people began to understand the nature of chemical elements. We still did not know anything about isotopes; if you told me that there are more than 20 silicon isotopes, I would not even understand your statement:



I am amazed that today mankind can classify individual atoms by the number of neutrons. The silicon spheres of the Avogadro project consist of 99.995% silicon 28:



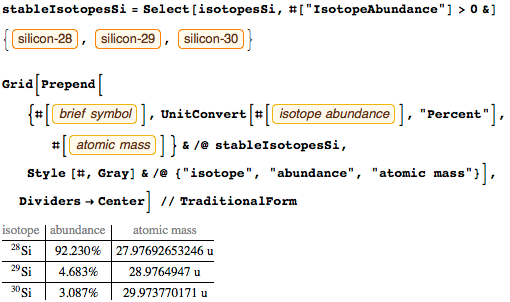
As long as the mass comparators reach an accuracy of 10 ^-11 , they can only compare the masses and not determine them. The mass can be determined after the Planck constant gets a fixed value using the watt balance.

I believe that Planck's constant is one of the most exciting constants. However, it reigns in the microworld, and therefore is hardly noticeable on a macroscopic scale.

A few years ago, I was very upset that it seemed to me that our dream of creating definitions for units would never be realized. I lost my dream when the values ​​for the Planck constant from experiments with a watt balance and experiments with a silicon sphere of Avogadro were completely different. Therefore, what a relief it was for me to see that over the past few years all the discrepancies have been overcome! And now the working mass is again synchronized with the international prototype.

Before finishing, let me say a few words about the Planck constant. Planck's constant is an archetypal quantity; one could expect that it would appear in quantum-mechanical phenomena. And when the Planck constant tends to zero, we return to classical mechanics (in the singular limit). I thought so until recently. Since I attend the weekly lectures of Vladimir Arnold , which he began to give in the summer of 2010 after joining us, I have serious reservations about such simplistic views. In his lecture on multidimensional geometry, he considered a symplectic camel ; Since then, I have considered the Heisenberg uncertainty relation as a classic relic rather than a quantum property. And sinceWerner Heisenberg showed me an article by Brodsky-Hoyer about the distribution of ħ , I got a much more restrained look at the cube BZO (Bronstein-Zelmanov-Perch). And let's not forget about recent attempts to express quantum mechanics at all without resorting to the Planck constant. Despite the fact that we understand a lot in Planck’s constant and its obvious manifestations (such as the “conversion coefficient” between the frequency and energy of photons in a vacuum), I think that its deepest secrets have not yet been discovered. To unravel them, we need a long trip on a symplectic camel through the deserts of hypothetical multiversums. And Paul Dirac believes that the role of the Planck constant in classical mechanics is still not well understood.

For a long time, Max himself believed that in the phase space (classical or through the Wigner transform) the minimum volume will be of the order of its constant h . As one of the fathers of quantum mechanics, Max still follows conceptual designs, especially the decoherence program. He was struck when subplank structures were discovered 15 years ago . Eugene Wigner told me that he suspected the existence of such subtle structures as early as the late 1930s. Since then, he has loved playing with the constructions of the Wigner function for all kinds of hypergeometric potentials and quantum carpets.. His favorite is still the Wigner function of the Duffing oscillator. However, a high-precision solution of the non-stationary Schrödinger equations resulting from the construction of the Wigner function based on the fractional Fourier transform can be found faster. This is how the initial wave packet in the form of a Gaussian curve looks after three periods of external force. The blue rectangle represents the area of ​​the xp plane of area h :



Here are some enlarged images (colored according to the sign of the function) of the last Wigner function. Each square has an area of ​​4 h and shows various subplank structures:



The upcoming definition of a kilogram through the Planck constant is a serious intellectual and technological achievement of mankind. Behind it are two centuries of hard work in metrological institutes. This event lays some of the deepest physical truths discovered in the 20th century into the foundation of our system of units of measurement. Here, a whole bunch of conversion units and fundamental constants will become known with greater accuracy (make sure that you have a new CODATA form , and hold the cardwith the new values ​​of the constants with you until you memorize them by heart). This will open the way to new physics and new technologies. In the event that you decide to conduct your own experiments that determine the values ​​of the constants, keep in mind that the deadline for including the values ​​you received is July 1, 2017.

The transition from a platinum-iridium kilogram, historically denoted by a symbol , to a kilogram based on the Planck constant h can be well visualized graphically as a 3D object that contains both symbols. During rotation, you can see a smooth transition from the projection form from to h , representing over 200 years of progress in the field of metrology and physics: An



interested reader can order a beautiful 3D versionhere . This is the perfect gift for your significant person at Christmas (to be ready for the redefinition of 2018), and you can order it in the form of a pendant or earrings (available in various metals; platinum is obviously the most natural choice, but such a symbol will cost about $ 5,000, so the polished silver option is also good).

Here are some images of the golden versions of Toh3D:



I understand that not everyone is the way I am excited about these events. I am waiting for 2018 when a kilogram as a material artifact will resign and be replaced by a fundamental constant. The new SI will base the most important measurement standards on 21st century technology.

If you have any questions or have comments - do not be shy: write to me at jeancharlesdeborda@gmail.com; thanks to the latest advances in technological impact (EPR = ER), we have a faster connection with the Earth.

À tous les temps, à tous les peuples!