Dates among digits of Pi: some thoughts from the perspective of statistics and numerology

Michael Trott's translation of the post " Dates Everywhere in Pi (e)! Some Statistical and Numerological Musings about the Occurrences of Dates in the Digits of Pi ".
The code in the article can be downloaded here . Many
thanks to Kirill Guzenko. KirillGuzenko for help in translating and preparing the publication.

---

Contents
Get all dates for the last 100 years.
Find all dates in pi.
Statistics of all dates.
First dates.
Dates in other representations and other constants.

---

In a recent post (see translation of the post " 3/14/15 9:26:53 Celebration of the" Day of the Pi "of the century, as well as a story about how to get your very personal piece of pi " on Habré), Stephen Wolfram wrote about the unique position of the century-old day of pi and presented different examples of the contents of dates in digits of pi (hereinafter in decimal notation). In this post, I will examine the statistics of the distributions of all possible dates over the past 100 years in the first 10 million digits of pi. We will see that 99.998% of the digits are some kind of date, and that millions of dates can be found in the first ten million digits of pi.

I will focus on dates that can be given with no more than six digits. That is, I can uniquely set dates in the interval of 36 525 days, starting from March 15, 1915 and ending March 14, 2015.

Let's start with a graphical visualization of our theme for setting the mood.

Get all dates for the last 100 years

As usual, the day of pi this year fell on March 14th.



36 525 days have passed since the century-old pi day of the 20th century.



Create a list of all 36,525 dates in question.



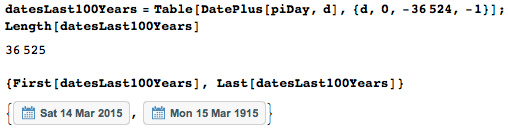
For further work, we define the function dateNumber , which for a given date returns the serial number of the date starting from the first (March 15, 1915 has number 1).



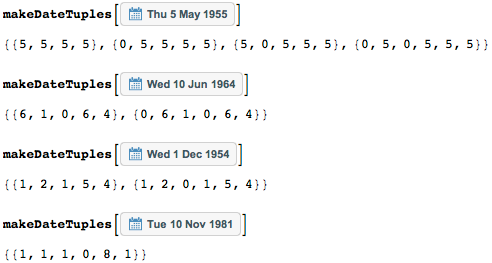
For the months from September to January, I will allow you to ask only one number - that is, 9 for September instead of 09; similarly for days. That is, some dates can be set by different sequences of digits. Function makeDateTuplesgenerates all sequences of integers representing dates. You can use several different date notations — always with zeros or always in short notation. With the optional inclusion of zeros in the days and months record, there will be more possible matches and more results, so I will use them in the future. (And if you prefer the usual format for recording dates in the form of day-month-year, then you just need to make changes to the makeDateTuples function ).



Dates can be represented in one, two, or four ways:



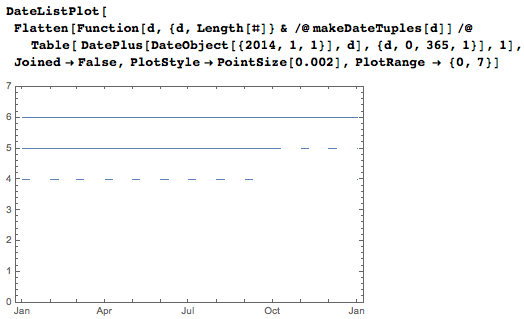
The following graph shows which days of the last year are represented by four, five, and six digits. The first nine days from January to September require four or five digits for recording, and the last days of October, November and December require six.



For fast (in constant time) recurring recognition of a sequence as a date, I will set the functions dateQ and datesOf . datesOf gives the normalized form of a sequence of date digits. We start by creating a pair of sequences and interpreting them as dates.



Here are some examples.



Most (77,350) sequences can be unambiguously construed as dates; some (2700) have two possible interpretations.



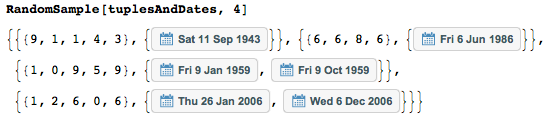
Here are some of the two-digit sequence of numbers.



The sequence {1,2,1,5,4} has two interpretations - as of January 21, 1954 or as of December 1, 1954 - restored using the datesOf function .



These are the quantities of four-, five-, and six-digit representations of dates.



And this is the number of definitions for each of the types set for the datesOf function .

Find all dates in pi

For all further calculations, I will use the first ten million decimal digits of pi (later it will be shown that ten million is enough to find any date in them). We can easily replace pi with any other constant (the code is universal).



Instead of using the complete sequence of numbers as a string, I will use a sequence of numbers divided into (overlapping) sequences. Now you can quickly and independently work with each sequence. And I indexed the sequence with the sequence numbers. For example:



Using the dateQ and datesOf functions defined above, I can now quickly find all sequences of digits that can be interpreted as dates.



Here are some interpretations of dates found. Each sublist has the form:

{date, startingDigit, digitSequenceRepresentingTheDate}
(date, start digit, sequence of digits representing the date).



We found about 8.1 million dates, represented by four numbers ; about 3.8 million dates - five ; about 365 thousand dates - six , totaling more than 12 million dates .



Note that I could use string processing functions (especially StringPosition ) to find the positions of date sequences. And of course, I would get the same result.



While using StringPosition would be good for finding a single date, working with all 35,000 sequences would take much longer.



Let's stop for a second and look at the counter of the found sequences of 4 digits. Of the 10,000 possible four-digit sequences, 8,100 are used, each of them appearing on average (1/10) ⁴ * 10⁷ = 10⁴ times, which follows from the “randomness” of the distribution of digits of pi. I guess the standard deviation should be around 1000 ^ ½≈31.6. A small calculation and graph confirm these figures.



The distribution curve of the number of different dates of four digits has the expected form of a bell.



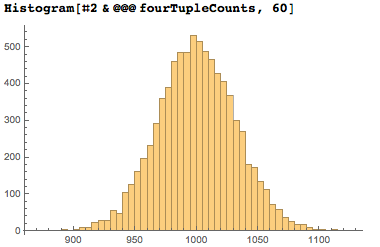
And the next graph shows how often each of the 4-digit sequences that represents a date appears in the first ten million digits of pi in decimal. We numbered all 4-digit sequences by combining numbers into a number; as a result, you can see empty vertical stripes in areas in which 4-digit sequences do not represent a date.



We now continue to process the found date positions. Group the results into lists of the same dates.



And in fact, in the first 10 million digits all dates are found , that is, it turns out that 36,525 different dates were found (we will see later that the choice of the number of digits for analysis was optimal).



Here's what a typical dateGroups member looks like .

Statistics of all dates

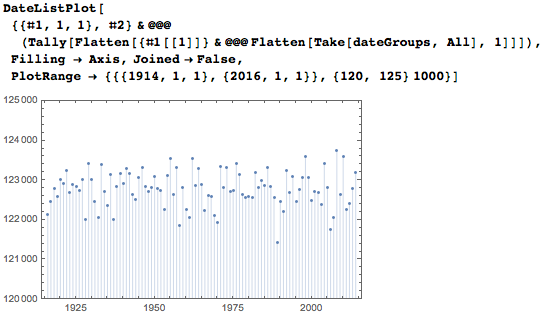
Now consider the data found in terms of statistics. Here is the number of occurrences of each date in the first ten million digits of pi. It is interesting, and maybe even somewhat unexpectedly, but many dates occur hundreds of times. Periodically occurring vertical stripes appear due to the quarter October-November-December.



The average distance between dates also clearly shows the early appearance of four-digit records of years with average intervals of less than 10,000, five-digit ones correspond to intervals of about 100,000, six-digit ones correspond to about 1,000,000.



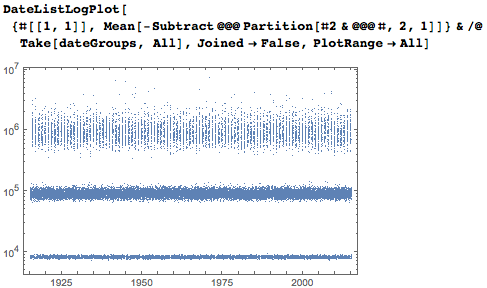
To facilitate readability, I formatted the triples {date, StartingPosition, dateDigitSequence} individually.



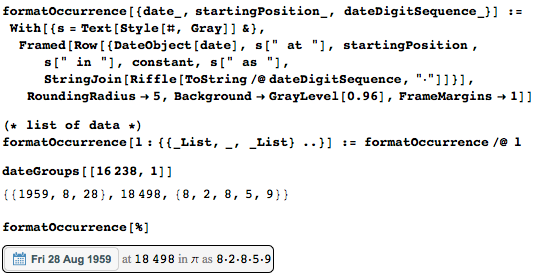
The most common date among the first 10 million digits - August 6, 1939 - occurs 1,362 times.



Let's find now the rarest. These three dates are found only once.



And these are two each (the output is shortened to save space).



Here is the distribution of the number of occurrences of dates. Three peaks corresponding to four-, five- and six-digit representations of dates (from left to right) are clearly different. Dates that are represented by sequences of 6 digits occur infrequently; as shown above, appear on average about 1200 times.



You can also collect and display dates by year (lower values ​​at the ends appear due to truncation of dates to ensure their uniqueness). The distribution is almost uniform.



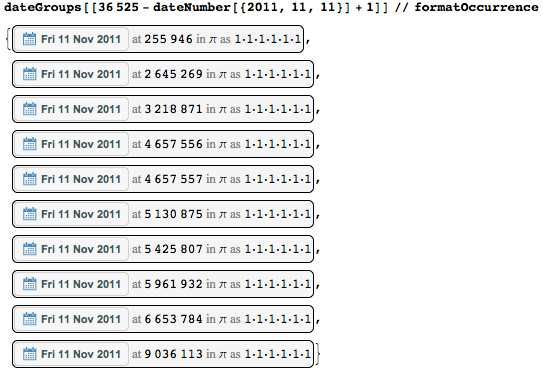
Let's look at dates with beautiful sequences of numbers and how often they appear. Since the results in dateGroupssorted by date, I can easily access the specified dates. Say, where is the date 11-11-11?



And the date is 1-23-45?



None of the dates starts at its own position (that is, there are no examples like the fact that January 1, 1945 [1-1-4-5] is at position 1145).



But there is one “palindromic case”: March 3, 1985 (3.3.8.5) lies at the palindrome position 5833.



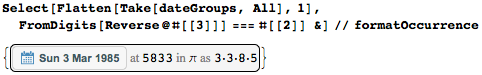
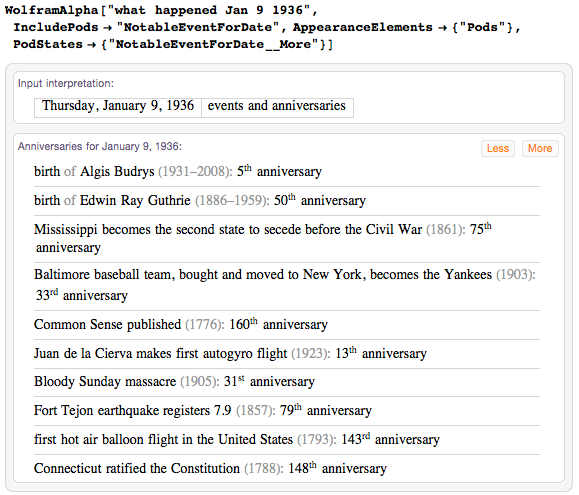
A very special date is January 9, 1936: it appears at the position of the 1936th prime number - 16,747.



Let's look at the memorable events on this day in history.



Since there was not a single date that would appear in its position, we can soften the conditions and find all the dates that “overlap” their positions.



And more than 100 times in the first 10 million digits of pi you can find the well-known combination of the first digits of pi - 314159.



Among pi you can find not only the dates of births, but also the days of physical constants, such as ħ-day (the day of the reduced Planck constant ), which, for example, was celebrated as centuries-old on October 5, 1945.



Here are the positions for matching dates.



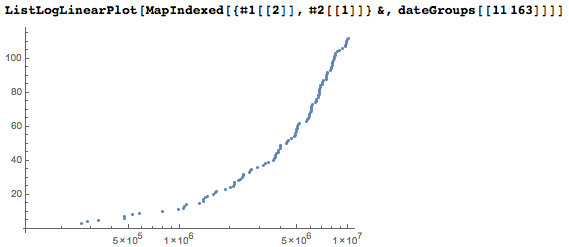
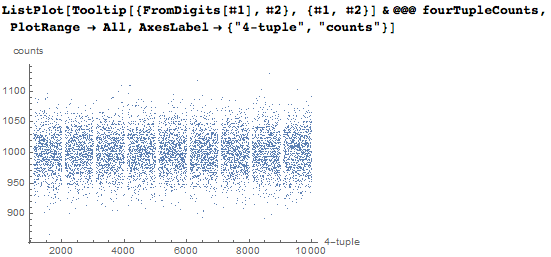
And here is an attempt to visualize the occurrence of all dates. In the date-digit plane, we set the points for the beginning of each date. We use a logarithmic scale for the positions of numbers, and as a result, the number of points is much larger at the top of the graph.



For dates that appear early in numerical order, the final volume of dates in numbers can also be visualized. Dates are four to six digits. The following graph shows the digits of all dates that begin in the first 10,000 digits.



After coarsening, the distribution becomes fairly uniform.



Until now, I took the date and looked at what position it begins in the sequence of digits of pi. Now let's do the opposite: how many dates contain a given digit of pi? To find the total number of dates for each digit, you can cycle through the dates.



It turns out up to 20 dates for each digit.



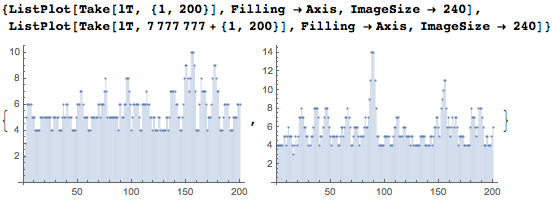
Here are two intervals of 200 digits each. We see that most numbers are in dates.



I noted above that I had about 12 million dates in the sequence of numbers. The sequence of digits that I used is only ten million digits long, and each date contains about five digits. This means that all these dates need about 60 million digits. It follows that many of the ten million digits must be reused - on average about five times. Only 2005 of the first ten million digits is not used in any of the sequences interpreted as dates, and this means that 99.98% of all digits are used in dates (not all are in the first position).



And here is a histogram of the distribution of the number of dates present on each specific digit. You can clearly see without much calculation that on average there are about 6 dates per digit.



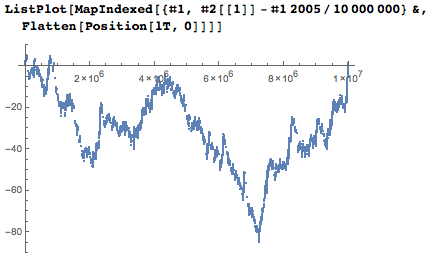
2005 non-date digits are fairly evenly distributed in the first ten million digits.



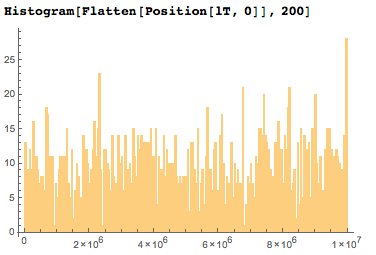
If I depict the specific positions of the idle numbers compared to their expected average position, then I get something like a random walk graph.



So, with whom are unused numbers bordered? There are 162 different 5-digit neighborhoods. Looking at them, you can immediately see why the central figure cannot be part of the date: there are too many zeros in the district .



And the largest unused block of numbers is six digits between positions 8,127,088 and 8,127,093.



In most digits, dates of different years overlap. The chart below shows the range of years from early to late, as a function of the position of the number.

Here are the unused numbers along with three left and three right neighbors.



In order to illustrate the operation of the algorithm above, I will take a random number and find all the dates that cover it.



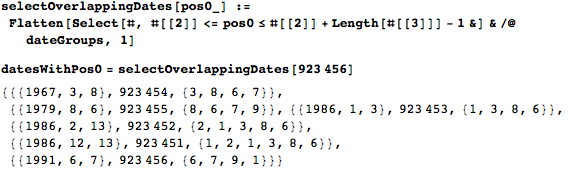
And here is a visualization of the “overlay” of dates.





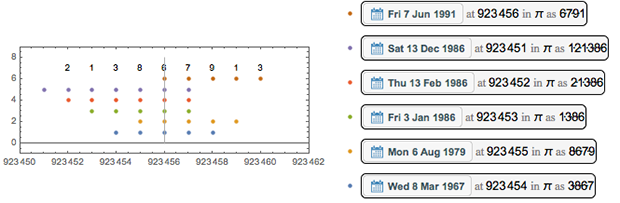
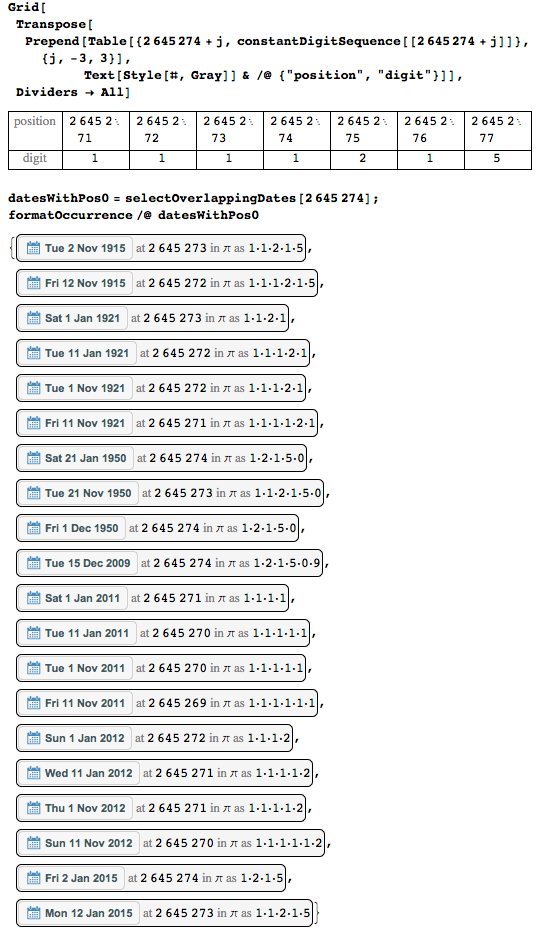
The most used number is the unit at position 2 645 274 - it is present in 20 different dates.



Here are the numbers in her neighborhood and the possible dates.



If I build the years, starting with a given digit for a larger number of digits (say, for the first 10,000), then I will see a relatively dense date cover on the digit-date plane.



Let's now plot the related dates. We will consider two dates to be related if they have at least one common digit (not necessarily the initial one).



The same graph is shown below, only for the first 600 digits, but with dedicated communities.



We now calculate the average distance between two occurrences of the same date.

First dates

The most interesting are the first appearances of dates, so let's extract them. We will work with two versions of the date list, the first is a list of lists of the form {date, first date position} ( firstOccurrences ), and the second is the same list sorted by position number in pi digits ( firstOccurrencesSortedByOccurrence ).



All possible interpretations of dates in the first ten digits of pi.



Or here's the other extreme - dates that occur for the first time as late as possible.



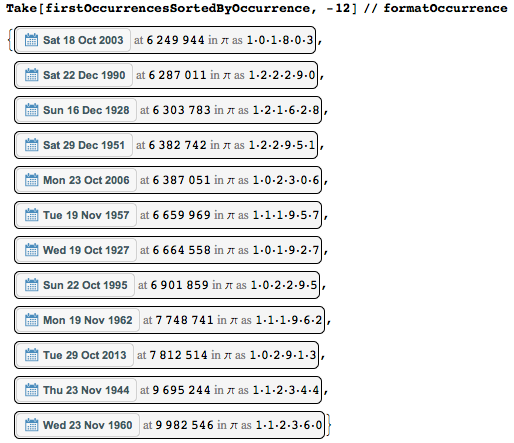
You can see that Wednesday, November 23, 1960 begins only at position 9 982 546 (= 2 * 7 * 713039) - so, using only the first ten million digits, I was lucky to catch it. Here is a quick direct check of this "record" date.



And who are the lucky ones from famous people who are fortunate enough to be born on this day?



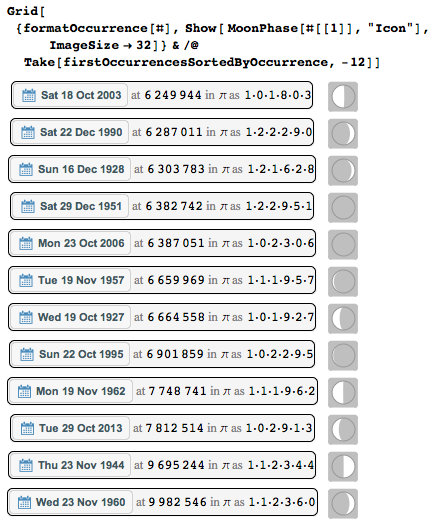
And in what phases was the moon during each of the top 10 most “deeply buried" dates?



And while Wednesday November 23, 1960 is the farthest date in a decimal sequence of digits, the most recent position as a prime corresponds to the date October 22, 1995.



In general, less than 10% of all dates appear on positions as prime numbers .



Often, some send digits of pi in a certain direction on the plane, forming random walks. We will do the same depending on the distance between the first occurrences of dates. We obtain images of typical two-dimensional random walks.



Here are the positions of the first appearance of dates in the last few years. Bursts in October, November and December of each year are caused by the need to set dates in sequences of five or six digits, while from January to September, dates can be set with fewer digits if you skip optional zeros.



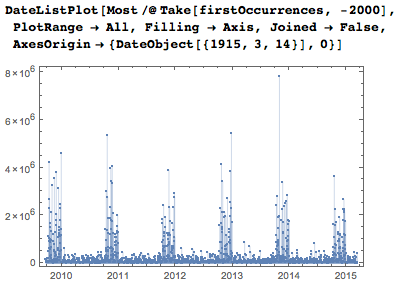
If I include all the dates, I will, of course, get much more “tight” charts.



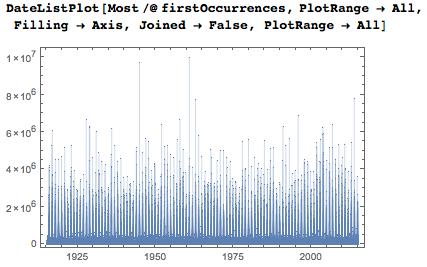
The logarithmic vertical axis shows that most dates first appear between thousandths and millionths.



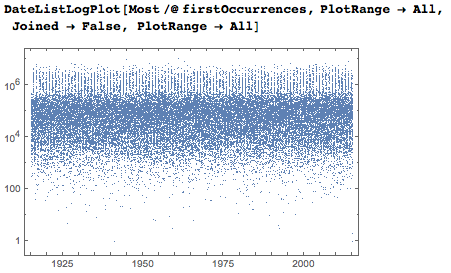
To get a deeper and more intuitive understanding of the general homogeneity and local “accidents” in a sequence of numbers (and, consequently, in dates), I will give a Voronoi diagram in the days-digits plane based on the points of the first occurrences of dates. The decrease in density with increasing numbers is due to the fact that I considered only the first occurrences of dates.



Easter Sunday is a great date for visualization, as every year it falls on different days.



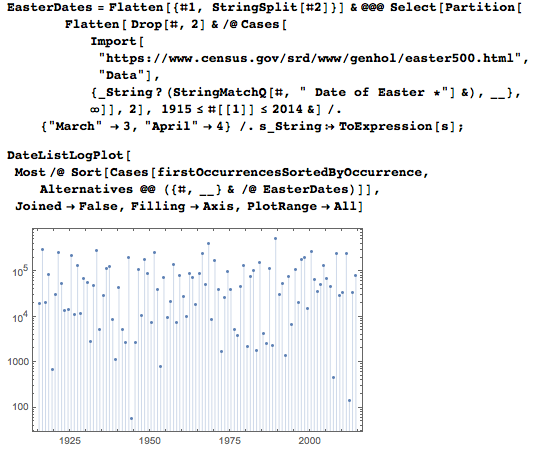
The average position of the first occurrence of a date, as a function of the number of digits needed to indicate it, depends, of course, on the number of digits needed to encode it.



The average position of the first appearance of the date falls on 239,083, but due to a spread of several million digits, the standard deviation is much larger.



Here are the first occurrences of “good” dates formed by repeating a single digit.



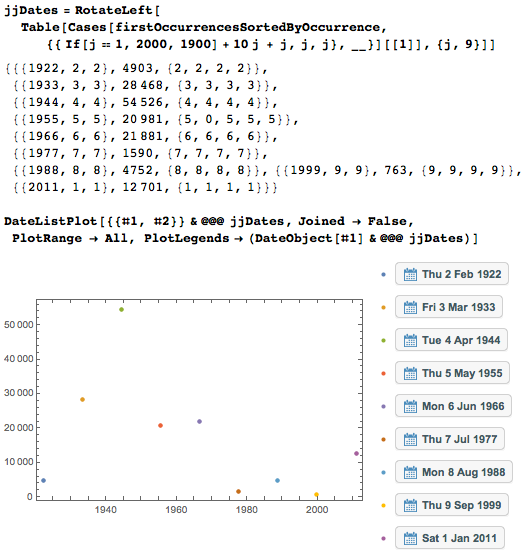
A detailed distribution of the number of occurrences of the first dates has the highest density in the first several tens of thousands of digits.



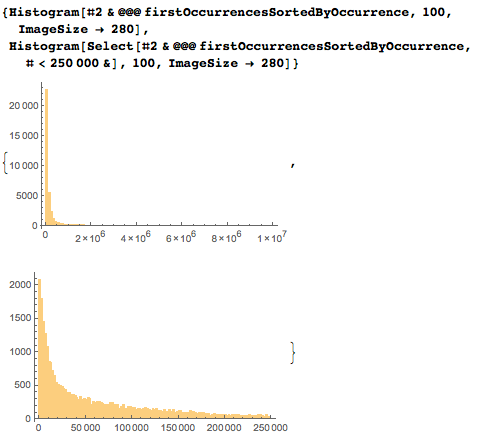
Logarithmic axes are much better suited to demonstrate distribution, however, due to the increase in cell size, the interpretation of the maximum should be taken carefully.



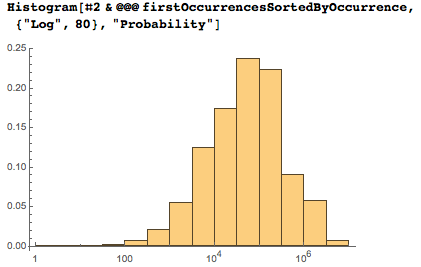
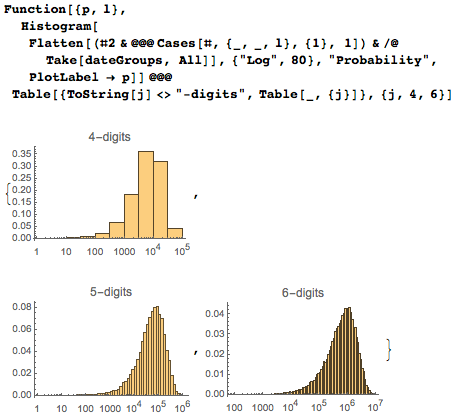
The last distribution is essentially a weighted superposition of the first occurrences of four-, five-, and six-digit sequences.



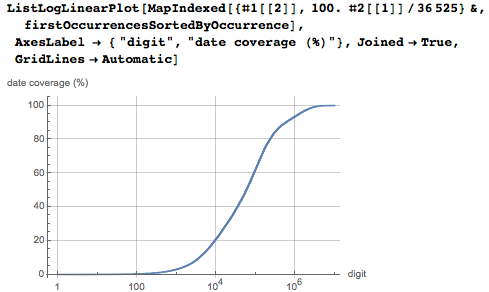
And here is the cumulative distribution of dates depending on the position of the number. You can see that the first 1% of ten million digits already contains 60% of all dates.



Even dates have slightly more dates than odd ones.



You can do the same for numbers, a multiple of three, four and so on. The left image shows the deviation of each class of correspondences from the average value, and the right one shows the largest matches examined by the parity criterion.



Actual numbers of first occurrences in each specific year fluctuate around the average.



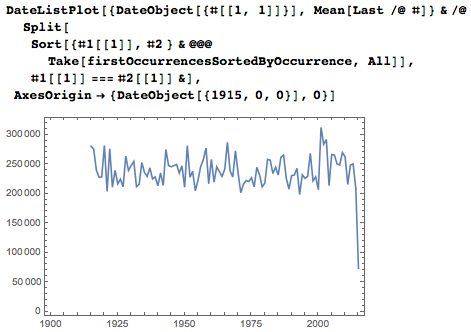
The average dates of the first occurrences of dates sorted by month clearly separate the two-digit and single-digit records for the months.



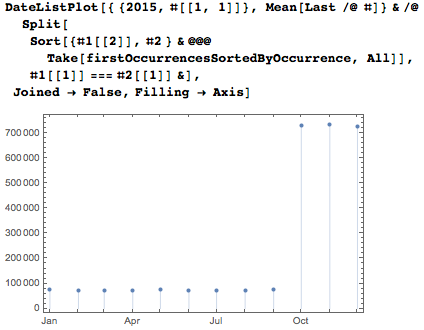
The averages for the days of the month (1-31) are mainly slowly increasing functions.



Finally, here are the average days of the week. Most of the first occurrences for dates are dates that match the environment.



I noted above that most numbers are on some dates. Only a small number of digits are contained in dates that appear for the first time (121,470).



Some of the positions of the sequences overlap in any case, and I can form a network of chains of dates with overlapping sequences of numbers.



The following graph shows the increasing sizes of the gaps between consecutive dates.



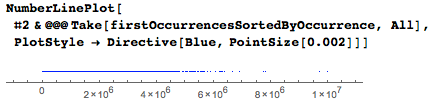
Spacing distribution:



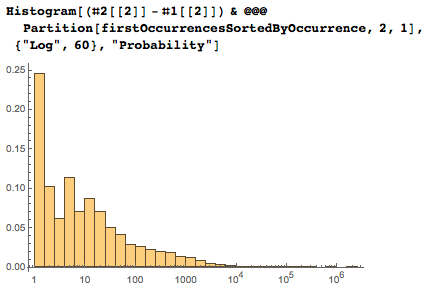
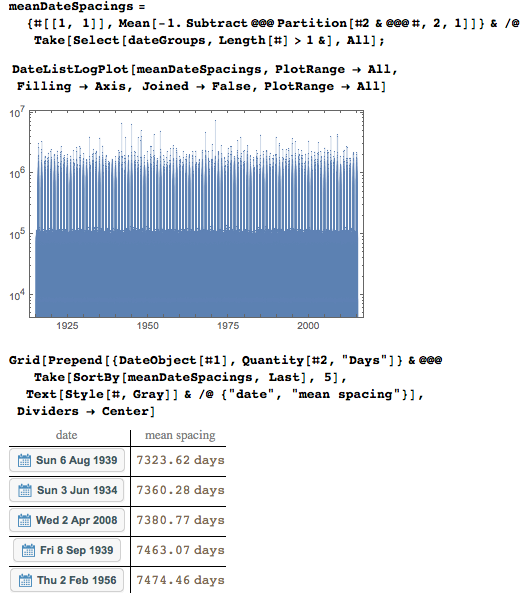
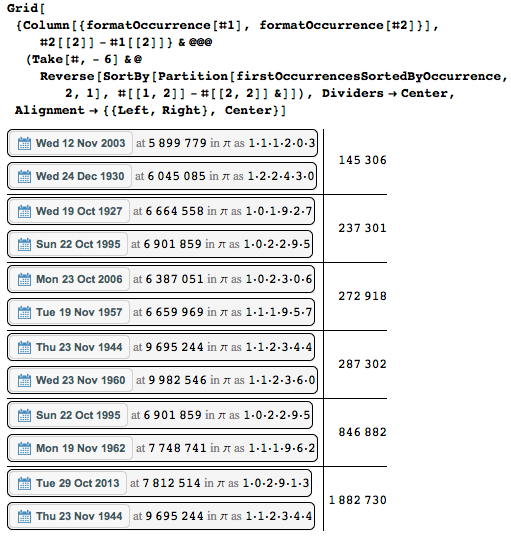
Here are the pairs of consecutive dates most distant from each other. In the penultimate figure, large gaps are clearly visible.

Dates in other representations and other constants

Now we will consider special dates in which the left parts of a continued fraction (numbers before a plus sign) coincide with numbers in decimal representation.



This gives the following line of the continued fraction of pi:



And, interestingly, there is only one such day.



None of the calculations performed so far have been carried out with respect to the digits pi. The numbers of any other irrational numbers (or even reasonably long rational numbers) contain dates. It was interesting to find many numerical expressions that contain the dates of this year (2015). Here they are brought together in an interactive demo.

Now we have come to the end of our thoughts. As a final example, let's try to interpret the positions of the numbers as seconds after the pi time this year, which happened on March 14 at 9:26:53. How long will I have to wait for the sequence of digits 3 • 1 • 4 • 1 • 5 in the decimal representation of other constants? Is it possible to find an expression (small), in the first million digits of which the sequence 3 • 1 • 4 • 1 • 5 does not fall? (Most of the elements of the following list ξs are random expressions. The last elements were found when searching for expressions that have a sequence of digits 3 • 1 • 4 • 1 • 5 as far as possible)



Here are two rational numbers that in decimal notation contain a sequence of digits:



And here are two integers with the initial digits of pi.



Using the new TimelinePlot function that Brett Champion described in his last post in the post (see the post " New in Wolfram Language: TimelinePlot function for creating a timeline " on Habré), I can easily show how long I have to wait.



We urge readers to conduct a deeper study of dates in digits of pi, or to consider instead of pi another constant (for example, Euler’s number e ), and possibly even in a different number system. In general, quality structures will be the same for almost all irrational numbers (to see a different picture, try ChampernowneNumber constant[10]). Will the first ten million digits of e contain all dates? And what position will be on October 21, 2014? What special dates are contained in other constants? These and many other questions await their answers.