Designing window functions that sum up to a unit with a given level of overlap
- Tutorial
There are a number of tasks in which the time-consuming signal is divided into segments, each of which is processed separately. In particular, this approach is used to analyze the signal using the window Fourier transform, or vice versa, during synthesis; as well as spectral processing such as noise removal, tempo changes, nonlinear filtering, audio data compression, and others.
The splitting process itself is mathematically represented by multiplying by some weight ( window ) function with offset. For the simplest window — rectangular — it might look like this:
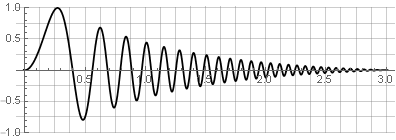
Source signal:
Splitting:
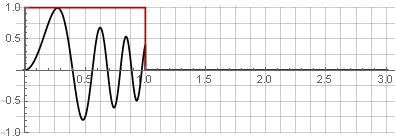
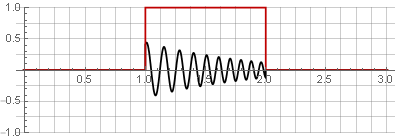
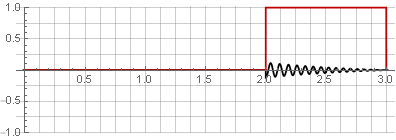
You can restore the original signal by simply summing them up.
However byFor some reasons, a rectangular function is not the best window function. When spectral analysis through the (usually fast) discrete Fourier transform, the analyzed data block seems to be "looping", which leads to a break at the edges and distortion of the spectrum:
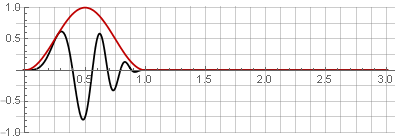
It is not suitable for reverse synthesis either - because any change will also lead to breaks - for example, We will try to reverse one of the parts:

To eliminate these shortcomings, overlapping is used - when each next window captures part of the data from the previous one; and the weight window, respectively, smoothly falls to the edges.
Most often, the Hanna window is used for this (also known as “raised cosine”) with an overlap of 50%:



Due to the symmetry of the cosine function when added, they are added to one:
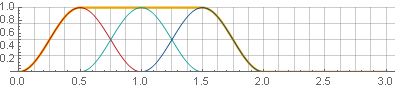
Now, in the reverse synthesis, we will not get gaps - but only if on the borders of the window, the values will still go to zero. For example, when reversing one of the parts, the smoothness is not disturbed:
Let us consider in more detail the algorithm for signal processing using the fast Fourier transform (FFT):
In this case, if the spectrum processing is not performed, the output signal must be identical to the input signal (only with the inevitable time delay).
When using the Hanna window, overlapping by 50% is no longer enough, since dips will arise:

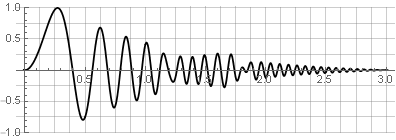
Since double overlap is equivalent to squaring, then the obvious solution would be to use the root from the Hanna window to compensate for squaring:
In this case, however, the window is no longer smooth at the edges - a gap appeared in the first derivative.
You can go the other way - use the overlap of 75%, and then the windows will also be added to a constant - just not in and in
and in  :
:
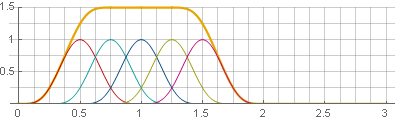
In this case, we just got lucky. If we decompose a square into an amount, then we can see that it is a composition of two Hanna windows, but at different scales, which allows us to fulfill the requirements we need:

With other window functions, such a focus will not work; Also, not all standard window functions can provide summation in a constant and at 50% overlap.
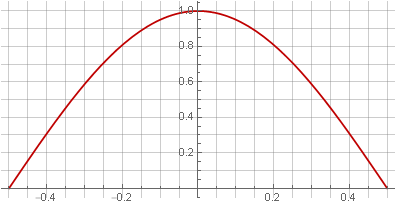
You can consider the Hanna window not as an independent function, but as the difference between two piecewise-continuous functions (a separate article was devoted to detailed consideration ) with offset. For example, using the following function

can write
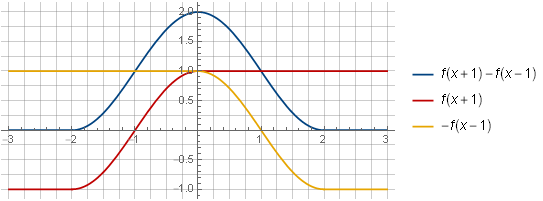
Having considered the components of the sum of two such windows, their ability to be summed into a constant will become more obvious:
On the segment![$ [0,2] $](https://habrastorage.org/getpro/habr/formulas/98b/516/89a/98b51689a10aaef9b3a0291415093dbe.svg) we received mutual compensation when adding functions
we received mutual compensation when adding functions  and
and  , insofar as
, insofar as 
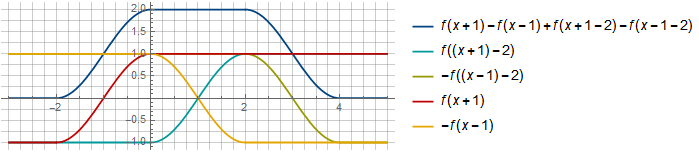
You can also select another offset, with a large overlap, for example:

And then, when offset in increments , they will also be summed up in a constant:
, they will also be summed up in a constant:

It is clear that if you rearrange the components of the window function, you get all the same windows Hannah.
Thus, using various functions of restriction, it is possible to form windows of the necessary form.
Now it remains to set the scale so that the definition areas and values do not depend on the size of the overlap. Defining a window on the interval![$ [0,1] $](https://habrastorage.org/getpro/habr/formulas/a5d/538/f83/a5d538f83bd73f9d1c9e8338db9a398a.svg) will get
will get
Where - piecewise continuous form function
- piecewise continuous form function
but - some interpolating function between points
- some interpolating function between points  and
and  .
.
Parameter determines the level of overlap - the divisor that determines the step to which each next window should be shifted,
determines the level of overlap - the divisor that determines the step to which each next window should be shifted,  , and must be greater than one,
, and must be greater than one,  .
.
Overlap percentage can be calculated by the formula
can be calculated by the formula
and vice versa
The final view of the window will depend on the choice of the level of overlap, and on the choice of the bounding function.
Here we will look at several ready-made solutions, for which everything was started. For simplicity, we will consider just the interpolating function. without any other strapping.
without any other strapping.
They are the least computationally expensive. Using the previously derived formula
we obtain a polynomial with a given number of zeros on higher derivatives that provide the necessary smoothness of the window at the edges.
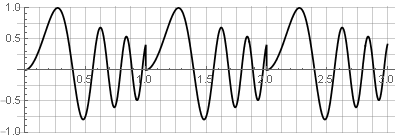
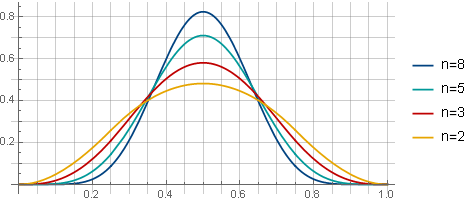
With an overlap of 75%, windows with different values of n will look like this:
And in the case of root extraction, this is how (using 75% overlap):

or this way (using 50% overlap):

Function
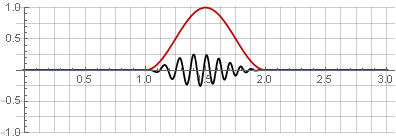
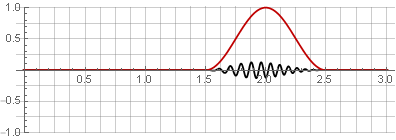
It is interesting because it is infinitely differentiable and all its derivatives at the edges are 0 (which can be proved by considering its derivatives based on the rules of differentiation - in each term there will be a multiplying factor). This allows building windows on its basis, all derivatives of which have no discontinuities:

The need for this type of window is caused by increasing the resolution of the FFT, but reducing the effect of the “time-frequency uncertainty” effect at high frequencies by increasing their concentration in the center.
First, we define the desired type of window function - for example, as follows:
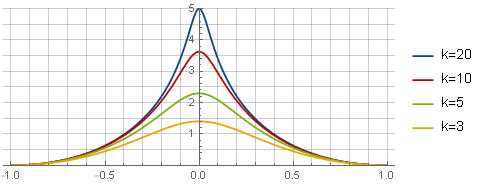
Here, the first term determines the type of the function itself, the second one provides the intersection with the abscissa axis, the third (parabola) zeroes the derivative at the edges for a smooth docking; and the parameter defines the "sharpness" of the top. In this form, it is not yet suitable for use - first, it is necessary to obtain the function of restriction from it through integration and scaling:
defines the "sharpness" of the top. In this form, it is not yet suitable for use - first, it is necessary to obtain the function of restriction from it through integration and scaling:
For convenience, you can bind the parameter overlap level
overlap level  - for example, so that the 4th derivative in the center of the window was 0 - and then
- for example, so that the 4th derivative in the center of the window was 0 - and then  will be counted as
will be counted as :
:
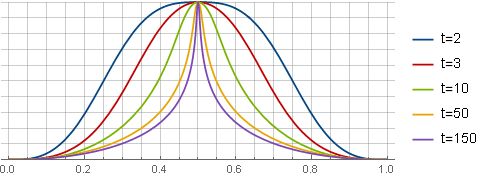
Here, for clarity, all windows are reduced to the same scale.
It is a more "aggressive" version of the previous window. As a basis, a hyperbole was chosen, from which, by successive transformations
and using the same steps in the form of integration and scaling got the formula
Here you can also bind the parameter to the level of overlap. Directly solving the 4th derivative equation is too cumbersome, so we’ll just make the solution for the previous window in the same way as
to the level of overlap. Directly solving the 4th derivative equation is too cumbersome, so we’ll just make the solution for the previous window in the same way as as
as  thus ensuring the role of the parameter
thus ensuring the role of the parameter  as “fine tuning”. With
as “fine tuning”. With windows will look like this:
windows will look like this:
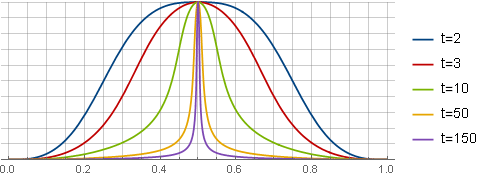
The window function does not necessarily have to be symmetrical. Suppose we need a window with a sharp attack and a smooth attenuation. We can get it according to the already familiar scheme - first determine the desired type of function, and then integrate to obtain the function of restriction. Here, the task is slightly complicated due to the fact that, due to asymmetry, the center will no longer pass through the origin, therefore an additional calculation step is added. This also leads to the fact that the formulas as a result are quite cumbersome. For example, consider the simplest option - a parabola multiplied by a polynomial weight window:

Here, the degree at x in the weighted window (namely, 10) determines the “sharpness” of the attack. We used a specific value, rather than a character parameter, to simplify the formulas for clarity - if you wish, you can recalculate it later.
After the integration, simply scaling is not enough - you need to even out the edges:

To do this, we first shift the function to the top to align the left edge, and then scale it to the two along the right edge and subtract the unit. Then we get the following formula:
In order for the final window to have the desired appearance, it is also necessary to ensure a sufficiently large level of overlap:

Similarly, you can build windows from any other bell-shaped functions — for example, Gaussians; and it is also possible to modify those already considered in order to provide greater smoothness or a change in the shape of the curve.
The spectral composition of such window functions has remained outside of consideration — separate studies should be devoted to this.
A slightly more advanced version of the article (with the ability to dynamically change the parameters in the windows under consideration and hidden formulas) in the form of a Wolfram Mathematica document can be downloaded here .
The splitting process itself is mathematically represented by multiplying by some weight ( window ) function with offset. For the simplest window — rectangular — it might look like this:
Source signal:

Splitting:



You can restore the original signal by simply summing them up.
Read more
However byFor some reasons, a rectangular function is not the best window function. When spectral analysis through the (usually fast) discrete Fourier transform, the analyzed data block seems to be "looping", which leads to a break at the edges and distortion of the spectrum:

It is not suitable for reverse synthesis either - because any change will also lead to breaks - for example, We will try to reverse one of the parts:

To eliminate these shortcomings, overlapping is used - when each next window captures part of the data from the previous one; and the weight window, respectively, smoothly falls to the edges.
50% overlap
Most often, the Hanna window is used for this (also known as “raised cosine”) with an overlap of 50%:






Due to the symmetry of the cosine function when added, they are added to one:

Now, in the reverse synthesis, we will not get gaps - but only if on the borders of the window, the values will still go to zero. For example, when reversing one of the parts, the smoothness is not disturbed:

Processing double overlay windows
Let us consider in more detail the algorithm for signal processing using the fast Fourier transform (FFT):
- splitting the signal into segments with overlapping windows;
- direct FFT;
- spectrum processing;
- reverse FFT;
- repeated window overlap (since after the inverse FFT the boundaries will not necessarily be joined to zero without a break);
- summation of the resulting segments.
In this case, if the spectrum processing is not performed, the output signal must be identical to the input signal (only with the inevitable time delay).
When using the Hanna window, overlapping by 50% is no longer enough, since dips will arise:

Since double overlap is equivalent to squaring, then the obvious solution would be to use the root from the Hanna window to compensate for squaring:

In this case, however, the window is no longer smooth at the edges - a gap appeared in the first derivative.
Note
Interestingly, in this case we got half the period of the sinusoid.
You can go the other way - use the overlap of 75%, and then the windows will also be added to a constant - just not in

In this case, we just got lucky. If we decompose a square into an amount, then we can see that it is a composition of two Hanna windows, but at different scales, which allows us to fulfill the requirements we need:

With other window functions, such a focus will not work; Also, not all standard window functions can provide summation in a constant and at 50% overlap.
Idea
You can consider the Hanna window not as an independent function, but as the difference between two piecewise-continuous functions (a separate article was devoted to detailed consideration ) with offset. For example, using the following function

can write

Having considered the components of the sum of two such windows, their ability to be summed into a constant will become more obvious:

On the segment
You can also select another offset, with a large overlap, for example:

And then, when offset in increments

It is clear that if you rearrange the components of the window function, you get all the same windows Hannah.
Thus, using various functions of restriction, it is possible to form windows of the necessary form.
Final formula
Now it remains to set the scale so that the definition areas and values do not depend on the size of the overlap. Defining a window on the interval
Where
but
Parameter
Overlap percentage
and vice versa
Note
When working with real data, it may be necessary to recalculate the level of overlap depending on the specific FFT size. For example, with FFT at 2048 points and a level of overlap of 3, we get a step of 2048/3 = 682.666 ..., which in practice is naturally unrealizable. Therefore round it to the whole, and we will recalculate as 2048/683 = 2.998535871156662 ...
we will recalculate as 2048/683 = 2.998535871156662 ...
Alternatively, you can do the opposite - use the window size that is known to be divisible by 3 (say 999), and the remainder to the required size for the FFT should be added with zeros (25th).
Alternatively, you can do the opposite - use the window size that is known to be divisible by 3 (say 999), and the remainder to the required size for the FFT should be added with zeros (25th).
The final view of the window will depend on the choice of the level of overlap, and on the choice of the bounding function.
Some interesting examples
Here we will look at several ready-made solutions, for which everything was started. For simplicity, we will consider just the interpolating function.
Polynomial windows
They are the least computationally expensive. Using the previously derived formula
we obtain a polynomial with a given number of zeros on higher derivatives that provide the necessary smoothness of the window at the edges.
first 10 polynomials
With an overlap of 75%, windows with different values of n will look like this:

And in the case of root extraction, this is how (using 75% overlap):

or this way (using 50% overlap):

Maximum smooth window
Function
It is interesting because it is infinitely differentiable and all its derivatives at the edges are 0 (which can be proved by considering its derivatives based on the rules of differentiation - in each term there will be a multiplying factor). This allows building windows on its basis, all derivatives of which have no discontinuities:

Window "skirt"
The need for this type of window is caused by increasing the resolution of the FFT, but reducing the effect of the “time-frequency uncertainty” effect at high frequencies by increasing their concentration in the center.
First, we define the desired type of window function - for example, as follows:

Here, the first term determines the type of the function itself, the second one provides the intersection with the abscissa axis, the third (parabola) zeroes the derivative at the edges for a smooth docking; and the parameter
For convenience, you can bind the parameter

Here, for clarity, all windows are reduced to the same scale.
Needle View Window
It is a more "aggressive" version of the previous window. As a basis, a hyperbole was chosen, from which, by successive transformations
and using the same steps in the form of integration and scaling got the formula
Here you can also bind the parameter

Asymmetrical window
The window function does not necessarily have to be symmetrical. Suppose we need a window with a sharp attack and a smooth attenuation. We can get it according to the already familiar scheme - first determine the desired type of function, and then integrate to obtain the function of restriction. Here, the task is slightly complicated due to the fact that, due to asymmetry, the center will no longer pass through the origin, therefore an additional calculation step is added. This also leads to the fact that the formulas as a result are quite cumbersome. For example, consider the simplest option - a parabola multiplied by a polynomial weight window:

Here, the degree at x in the weighted window (namely, 10) determines the “sharpness” of the attack. We used a specific value, rather than a character parameter, to simplify the formulas for clarity - if you wish, you can recalculate it later.
After the integration, simply scaling is not enough - you need to even out the edges:

To do this, we first shift the function to the top to align the left edge, and then scale it to the two along the right edge and subtract the unit. Then we get the following formula:
In order for the final window to have the desired appearance, it is also necessary to ensure a sufficiently large level of overlap:

Conclusion
Similarly, you can build windows from any other bell-shaped functions — for example, Gaussians; and it is also possible to modify those already considered in order to provide greater smoothness or a change in the shape of the curve.
The spectral composition of such window functions has remained outside of consideration — separate studies should be devoted to this.
A slightly more advanced version of the article (with the ability to dynamically change the parameters in the windows under consideration and hidden formulas) in the form of a Wolfram Mathematica document can be downloaded here .
