Step-by-step operation of GOST R 34.12-2015 in ECB mode
Grasshopper in ECB mode
Not so long ago, an article appeared on the new standard for block encryption - GOST R 34.12-2015. In which all the innovations of this algorithm are described in sufficient detail. In this article I will try to explain the step-by-step operation of the algorithm in a simple replacement mode, so that users can more clearly appreciate the advantages of the domestic standard. In the process of deploying round keys and in encryption mode, the same transformations are used, so we won’t take this issue separately. For a better understanding, each transformation will explain part of the standard implementation code in C ++. So, let's get started.
We have the plaintext a = 1122334455667700ffeeddccbbaa9988 and the master key key =8899aabbccddeeff0011223344556677fedcba98765432100123456789abcdef .
The first conversion is a bitwise addition modulo 2 of the plaintext and the first round key, that is:
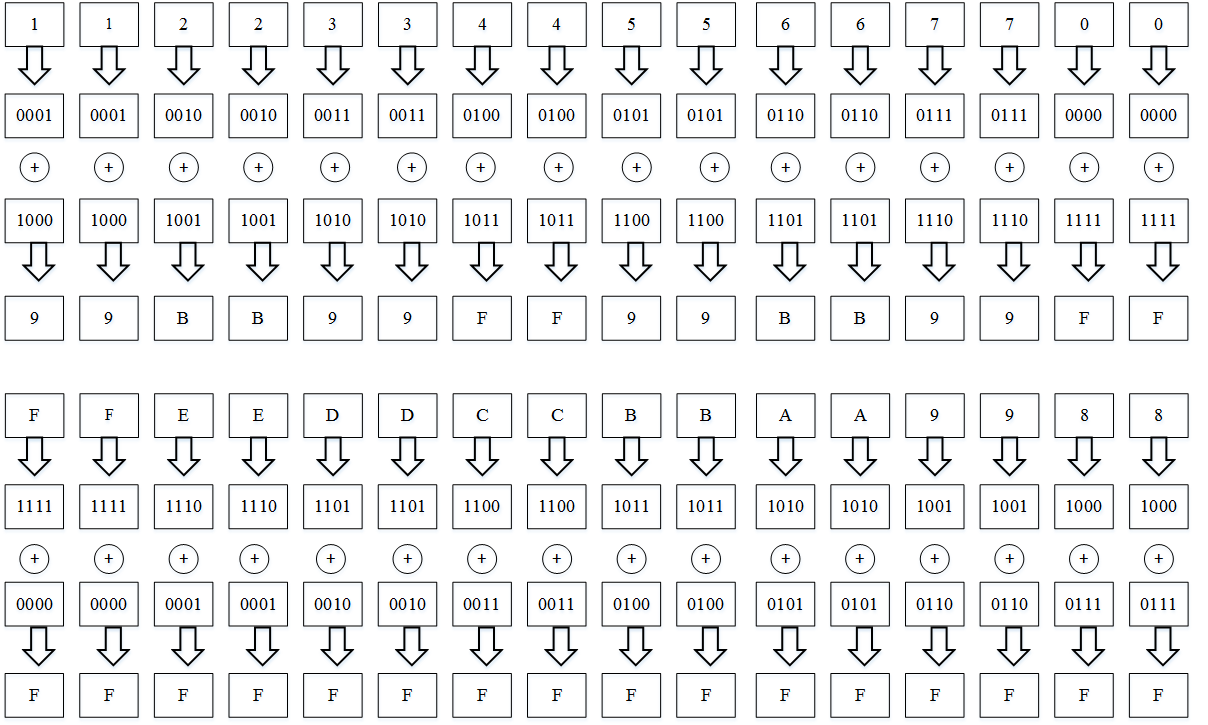
X transformation: a-plaintext, b-round key (matches the older part of the master key), outdata-result of the conversion.
int funcX(unsigned char* a, unsigned char* b, unsigned char* outdata) {
for (int i = 0; i < 16; ++i) {
outdata[i] = a[i] ^ b[i];
}
return -1;
}
The result of the first conversion is a 128-bit vector, it is 99BB99FF99BB99FFFFFFFFFFFFFFFFFFFF . The second transformation of the algorithm is a nonlinear bijective transformation of the vector obtained after the first operation using a substitution block. It works as follows: a
128-bit vector after modulo two is converted by byte into decimal form, thereby determining the position of the byte in the lookup table (S-block), then a decimal number is read from this position and converted back to hexadecimal. For example, the hexadecimal number 99 corresponds to the decimal 153. The element number 153 in the lookup table has a value of 232, which corresponds to the hexadecimal E8.
For our initial data, this transformation will look as follows:
Transformation S (indata-result of X-conversion, outdata-result of S-conversion):
void funcS(unsigned char* indata, unsigned char* outdata) {
for (int i = 0; i < 16; ++i) {
outdata[i] = kPi[indata[i]];
}
}
kPi-array is the same S-block.
The next step in encryption is linear conversion, performed using a linear feedback shift register. It works as follows: first, the result of the S-conversion is read by byte, then each byte read is multiplied by 256 (this is necessary to calculate the position of the number in the table.h table with all possible multiplication results in the GF field (2 ^ n) according to GOST). The number is read from the position, the coefficient 148, 32, 133, 16, 194, 192, 1, 251, 1, 192, 194, 16, 133, 32, 148, 1 is added to itdepending on the iteration number, this happens with the following bytes. Bytes are added together modulo two and all 128 bits (the result of the S-conversion) are shifted towards the low order, and the resulting number in hexadecimal is written in place of the read byte. The register is shifted and overwritten 16 times.
Convert R (indata-result of S-conversion, outdata-result of a single shift of the register):
int funcR(unsigned char * indata, unsigned char *outdata) {
unsigned long sum = 0;
for (int i = 0; i < 16; ++i) {
sum ^= multTable[indata[i] * 256 + kB[i]];
}
outdata[0] = sum;
memcpy(outdata + 1, indata, 15);
return -1;
}
Directly L-conversion:
int funcL(unsigned char* indata, unsigned char* outdata) {
unsigned char tmp[16];
int i = 0;
memcpy(tmp, indata, 16);
for (i = 0; i < 16; ++i) {
funcR(tmp, outdata);
memcpy(tmp, outdata, 16);
}
return 0;
}
The result of the L-conversion will be the following 128-bit vector E297B686E355B0A1CF4A2F9249140830 This is the result of the first round of the algorithm, the next 8 rounds will go the same way, you can see the results of their work in the description of the standard. The final 10 round includes only X-transformation of the results of 9 rounds and the key of 10 rounds.
For those who are too lazy to delve into the source code of the Grasshopper implementation
Nonlinear bijective transformation
Inverse nonlinear bijective transformation of a set of binary vectors:
Multiplication factors in the formation of l:
Convert X:
Convert S:
Conversion R:
Inverse Transformation S:
Inverse L transformation:
Inverse Transformation R:
The function of generating iterative keys:
The function of generating iterative constants:
A slightly modified procedure for obtaining round keys:
static const unsigned char kPi[256] = {
252, 238, 221, 17, 207, 110, 49, 22, 251, 196, 250, 218, 35, 197, 4, 77,
233, 119, 240, 219, 147, 46, 153, 186, 23, 54, 241, 187, 20, 205, 95, 193,
249, 24, 101, 90, 226, 92, 239, 33, 129, 28, 60, 66, 139, 1, 142, 79, 5,
132, 2, 174, 227, 106, 143, 160, 6, 11, 237, 152, 127, 212, 211, 31, 235,
52, 44, 81, 234, 200, 72, 171, 242, 42, 104, 162, 253, 58, 206, 204, 181,
112, 14, 86, 8, 12, 118, 18, 191, 114, 19, 71, 156, 183, 93, 135, 21, 161,
150, 41, 16, 123, 154, 199, 243, 145, 120, 111, 157, 158, 178, 177, 50, 117,
25, 61, 255, 53, 138, 126, 109, 84, 198, 128, 195, 189, 13, 87, 223, 245,
36, 169, 62, 168, 67, 201, 215, 121, 214, 246, 124, 34, 185, 3, 224, 15,
236, 222, 122, 148, 176, 188, 220, 232, 40, 80, 78, 51, 10, 74, 167, 151,
96, 115, 30, 0, 98, 68, 26, 184, 56, 130, 100, 159, 38, 65, 173, 69, 70,
146, 39, 94, 85, 47, 140, 163, 165, 125, 105, 213, 149, 59, 7, 88, 179, 64,
134, 172, 29, 247, 48, 55, 107, 228, 136, 217, 231, 137, 225, 27, 131, 73,
76, 63, 248, 254, 141, 83, 170, 144, 202, 216, 133, 97, 32, 113, 103, 164,
45, 43, 9, 91, 203, 155, 37, 208, 190, 229, 108, 82, 89, 166, 116, 210, 230,
244, 180, 192, 209, 102, 175, 194, 57, 75, 99, 182};
Inverse nonlinear bijective transformation of a set of binary vectors:
static const unsigned char kReversePi[256] = {
0xa5, 0x2d, 0x32, 0x8f, 0x0e, 0x30, 0x38, 0xc0, 0x54, 0xe6, 0x9e, 0x39,
0x55, 0x7e, 0x52, 0x91, 0x64, 0x03, 0x57, 0x5a, 0x1c, 0x60, 0x07, 0x18,
0x21, 0x72, 0xa8, 0xd1, 0x29, 0xc6, 0xa4, 0x3f, 0xe0, 0x27, 0x8d, 0x0c,
0x82, 0xea, 0xae, 0xb4, 0x9a, 0x63, 0x49, 0xe5, 0x42, 0xe4, 0x15, 0xb7,
0xc8, 0x06, 0x70, 0x9d, 0x41, 0x75, 0x19, 0xc9, 0xaa, 0xfc, 0x4d, 0xbf,
0x2a, 0x73, 0x84, 0xd5, 0xc3, 0xaf, 0x2b, 0x86, 0xa7, 0xb1, 0xb2, 0x5b,
0x46, 0xd3, 0x9f, 0xfd, 0xd4, 0x0f, 0x9c, 0x2f, 0x9b, 0x43, 0xef, 0xd9,
0x79, 0xb6, 0x53, 0x7f, 0xc1, 0xf0, 0x23, 0xe7, 0x25, 0x5e, 0xb5, 0x1e,
0xa2, 0xdf, 0xa6, 0xfe, 0xac, 0x22, 0xf9, 0xe2, 0x4a, 0xbc, 0x35, 0xca,
0xee, 0x78, 0x05, 0x6b, 0x51, 0xe1, 0x59, 0xa3, 0xf2, 0x71, 0x56, 0x11,
0x6a, 0x89, 0x94, 0x65, 0x8c, 0xbb, 0x77, 0x3c, 0x7b, 0x28, 0xab, 0xd2,
0x31, 0xde, 0xc4, 0x5f, 0xcc, 0xcf, 0x76, 0x2c, 0xb8, 0xd8, 0x2e, 0x36,
0xdb, 0x69, 0xb3, 0x14, 0x95, 0xbe, 0x62, 0xa1, 0x3b, 0x16, 0x66, 0xe9,
0x5c, 0x6c, 0x6d, 0xad, 0x37, 0x61, 0x4b, 0xb9, 0xe3, 0xba, 0xf1, 0xa0,
0x85, 0x83, 0xda, 0x47, 0xc5, 0xb0, 0x33, 0xfa, 0x96, 0x6f, 0x6e, 0xc2,
0xf6, 0x50, 0xff, 0x5d, 0xa9, 0x8e, 0x17, 0x1b, 0x97, 0x7d, 0xec, 0x58,
0xf7, 0x1f, 0xfb, 0x7c, 0x09, 0x0d, 0x7a, 0x67, 0x45, 0x87, 0xdc, 0xe8,
0x4f, 0x1d, 0x4e, 0x04, 0xeb, 0xf8, 0xf3, 0x3e, 0x3d, 0xbd, 0x8a, 0x88,
0xdd, 0xcd, 0x0b, 0x13, 0x98, 0x02, 0x93, 0x80, 0x90, 0xd0, 0x24, 0x34,
0xcb, 0xed, 0xf4, 0xce, 0x99, 0x10, 0x44, 0x40, 0x92, 0x3a, 0x01, 0x26,
0x12, 0x1a, 0x48, 0x68, 0xf5, 0x81, 0x8b, 0xc7, 0xd6, 0x20, 0x0a, 0x08,
0x00, 0x4c, 0xd7, 0x74};
Multiplication factors in the formation of l:
static const unsigned char kB[16] = {
148, 32, 133, 16, 194, 192, 1, 251, 1, 192, 194, 16, 133, 32, 148, 1};
Convert X:
int funcX(unsigned char* a, unsigned char* b, unsigned char* outdata)
{
for(int i = 0; i < 16; ++i)
{
outdata[i] = a[i] ^ b[i];
}
return -1;
}
Convert S:
void funcS(unsigned char* indata, unsigned char* outdata){
for(int i = 0; i < 16; ++i)
{
outdata[i] = kPi[indata[i]];
}
}
int funcL(unsigned char* indata, unsigned char* outdata)
{
unsigned char tmp[16];
int i = 0;
memcpy(tmp, indata, 16);
for(i = 0; i < 16; ++i)
{
funcR(tmp, outdata);
memcpy(tmp, outdata, 16);
}
return 0;
}
Conversion R:
int funcR(unsigned char * indata , unsigned char *outdata ){
unsigned long sum=0;
for(int i = 0; i < 16; ++i)
{
sum ^= multTable[indata[i]*256 + kB[i]];
}
outdata[0] = sum;
memcpy(outdata+1, indata, 15);
return -1;
}
Inverse Transformation S:
int funcReverseS(unsigned char* indata, unsigned char* outdata)
{
unsigned int i;
for(i = 0; i < 16; ++i)
{
outdata[i] = kReversePi[indata[i]];
}
return 0;
}
Inverse L transformation:
int funcReverseL(unsigned char* indata, unsigned char* outdata)
{
unsigned char tmp[16];
unsigned int i;
memcpy(tmp, indata, 16);
for(i = 0; i < 16; ++i)
{
funcReverseR(tmp, outdata);
memcpy(tmp, outdata, 16);
}
return 0;
}
Inverse Transformation R:
int funcReverseR(unsigned char* indata, unsigned char* outdata)
{
unsigned char tmp[16] = {0};
unsigned char sum = 0;
unsigned int i;
memcpy(tmp, indata+1, 15);
tmp[15] = indata[0];
for(i = 0; i < 16; ++i)
{
sum ^= multTable[tmp[i]*256 + kB[i]];
}
memcpy(outdata, tmp, 15);
outdata[15] = sum;
return 0;
}
The function of generating iterative keys:
int funcF(unsigned char* inputKey, unsigned char* inputKeySecond, unsigned char* iterationConst, unsigned char* outputKey, unsigned char* outputKeySecond)
{
unsigned char temp1[16] = {0};
unsigned char temp2[16] = {0};
funcLSX(inputKey, iterationConst, temp1);
funcX(temp1, inputKeySecond, temp2);
memcpy(outputKeySecond, inputKey, 16);
memcpy(outputKey, temp2, 16);
return 0;
}
The function of generating iterative constants:
int funcC(unsigned char number, unsigned char* output)
{
unsigned char tempI[16] = {0};
tempI[15] = number;
funcL(tempI, output);
return 0;
}
A slightly modified procedure for obtaining round keys:
int ExpandKey(unsigned char* masterKey, unsigned char mass[8][16] )
{
unsigned char C[16] = {0};
unsigned char temp1[16] = {0};
unsigned char temp2[16] = {0};
unsigned char j, i;
unsigned char keys[16];
int g=0;
memcpy(keys, masterKey, 16);
memcpy(keys + 16, masterKey + 16, 16);
memcpy(temp1, keys,16);
memcpy(temp1+16, keys+16,16);
for(j = 0; j < 4; ++j)
{
for( i = 1; i <8; ++i )
{
funcC(j*8+i, C);
funcF(temp1, temp2, C, temp1, temp2);
}
funcC(j*8+8, C);
funcF(temp1, temp2, C, temp1, temp2); //два следующих ключа!
memcpy(keys , temp1, 16);
memcpy(keys + 16, temp2, 16);
memcpy(mass[g],temp1,16);
g++;
memcpy(mass[g],temp2,16);
g++;
}
return 0;
}