Intervals in C ++, Part 4: to Infinity and Beyond
- Transfer
In the last part, I talked about the concept of incrementers (Iterable) and showed how they solve many problems inherent in standard intervals. Now I will expand this concept to make endless interval programming a safer and more efficient business.
Disclaimer : The ideas in this post are more speculative than in the previous ones. I will be happy to have a discussion .
In addition to the resolved problems that I talked about in previous posts, two more remained. It:
iota_range - an infinite range of integers starting from some value and lasting forever. This is a sorted forward spacing. Here are just binary search algorithms that work with sorted straight intervals, will not work with it. You cannot conquer infinity by division (a good phrase turned out).
Is it possible to fix STL algorithms so that they do not break when receiving an infinite interval? In their current form, no - it is impossible at the compilation stage to transmit information that some of the iterators denotes an infinite interval. Think about this: the following code will work for sure:
but this one will work forever:
If rng.begin () has the same type as rng.end (), two calls return the same lower_bound instance. A function cannot determine whether it will work forever or not. But if it is possible to allow the signal iterator to be of a different type, we will manage to carry out this check at the compilation stage.
Suppose we have a type function (metafunction) called DenotesInfiniteSequence, which takes a pair of types (BeginType, EndType) and says whether the sequence is infinite. We have already determined that if BeginType and EndType are the same, then DenotesInfiniteSequence should return false, since it will not be able to verify this in any way. But if they are different - let's say EndType will be of type unreachable_sentinel or something like that, then we will know at the compilation stage that the sequence is infinite.
Some intervals, by definition, will be infinite, even having the start and end iterators of the same type.
I would like to immediately catch such errors, but, obviously, the binary function DenotesInfiniteSequence can not cope with this. For zeros, the BeginType and EndType types will be the same, so DenotesInfiniteSequence will return false.
Therefore, we need to construct a unary function of IsInfinite types that accepts an interval type.
It can be used to define the concept of FiniteIterable.
Each FiniteIterable is Iterable. A parallel hierarchy of refinements is observed:
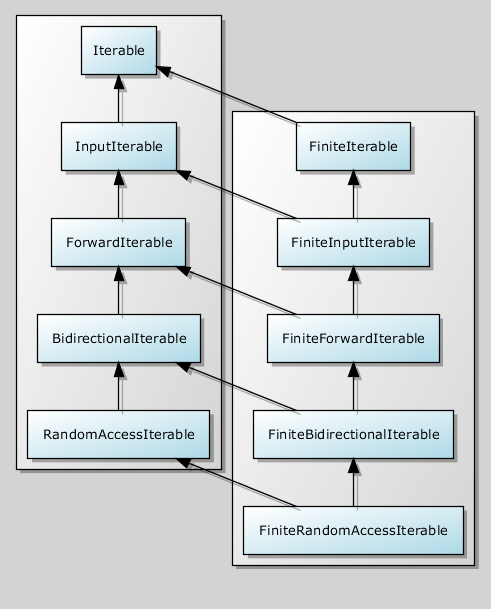
And all these concepts, by analogy with Range, do not need to be defined in the code. Finiteness is orthogonal to the Iterable hierarchy, and can be interrogated separately.
But why FiniteIterable and not InfiniteIterable? It's all about the algorithms and their requirements. There are no algorithms that require their interval arguments to be infinite. Therefore, it would be useless to be able to write InfiniteIterable. But an algorithm like lower_bound would like the interval to be finite. From this and FiniteIterable.
So, all iterators model FiniteIterable by default, and the type must somehow learn to be infinite. How? It is possible to specialize is_infinite. Fortunately, tools for creating incrementors and intervals accept the optional IsInfinite parameter, so this is easy to do. Here's what the zeroes class now looks like:
By adding the FiniteIterable concept, we give algorithms that require finiteness the opportunity to verify this at the compilation stage.
Now we need to divide the intervals into categories. In theory, either it is infinite or finite - is not it? No, actually. Take istream. It may be finite, it may not be. Usually the flow stops, but sometimes ...
The situation is complicated. Is it necessary to prohibit the transfer of istream to the algorithm only because it can be infinite?
At infinite intervals, there is such a difficulty: all iterators and all incrementors have a difference_type associated with them. Alexander Stepanov writes about this:
It turns out that we need a whole type of infinite size. Is there a solution to this problem?
Of course, I don’t like everything that slows down the operation of the algorithms, so std :: ptrdiff_t can be left as the difference_type by default. In addition, you need to design interval interfaces to give users the ability to set another difference_type if they care about overflow. Therefore, I like options 4 and 5. Other library types like bigint or safe_int with certain restrictions would be nice to be able to apply - if the user could specify their use, changing the speed to security when he needs it.
Perhaps, while reading previous posts, you were overly optimistic: everything seemed to be starting to work out, and now you are confused. But it seems to me that we have made good progress in comparison with where we started. I described 5 problems with intervals using a pair of iterators. The new concept of incrementors solves 3 of them, the 4th problem (infinite intervals) can theoretically be solved by improving this concept. And there are several options for working with the 5th (overflow). At least a start has been made.
Some ask if I plan to get my ideas across to the C ++ standardization committee. Of course. When we get support for concepts in the language, there will be a need for a conceptualized version of STL, possibly working in a different namespace.
In the meantime, I will discuss the issue on the SG9 (Ranges) mailing list (http://www.open-std.org/mailman/listinfo/ranges). This controversial issue is likely to generate new ideas. Interested persons are encouraged to join the discussion.
The author brought his ideas to the committee and is now engaged in their implementation.
Other articles in the series
Intervals in C ++, Part 1: Intervals with delimiters
Intervals in C ++, Part 2: Infinite Intervals
Intervals in C ++, Part 3: Introducing Iterables
Disclaimer : The ideas in this post are more speculative than in the previous ones. I will be happy to have a discussion .
In addition to the resolved problems that I talked about in previous posts, two more remained. It:
- Some STL algorithms do not work at infinite intervals
- Infinite or possibly infinite intervals lead to difference_type overflow
Infinite iterators
iota_range - an infinite range of integers starting from some value and lasting forever. This is a sorted forward spacing. Here are just binary search algorithms that work with sorted straight intervals, will not work with it. You cannot conquer infinity by division (a good phrase turned out).
Is it possible to fix STL algorithms so that they do not break when receiving an infinite interval? In their current form, no - it is impossible at the compilation stage to transmit information that some of the iterators denotes an infinite interval. Think about this: the following code will work for sure:
// быстро заканчивается:
iota_range rng;
auto i = std::lower_bound(rng.begin(),
std::next(rng.begin(), 10),
5);
but this one will work forever:
// будет работать «вечно» :'-(
iota_range rng;
auto i = std::lower_bound(rng.begin(),
rng.end(),
5);
If rng.begin () has the same type as rng.end (), two calls return the same lower_bound instance. A function cannot determine whether it will work forever or not. But if it is possible to allow the signal iterator to be of a different type, we will manage to carry out this check at the compilation stage.
Suppose we have a type function (metafunction) called DenotesInfiniteSequence, which takes a pair of types (BeginType, EndType) and says whether the sequence is infinite. We have already determined that if BeginType and EndType are the same, then DenotesInfiniteSequence should return false, since it will not be able to verify this in any way. But if they are different - let's say EndType will be of type unreachable_sentinel or something like that, then we will know at the compilation stage that the sequence is infinite.
Endless intervals
Some intervals, by definition, will be infinite, even having the start and end iterators of the same type.
// бесконечный интервал нулей
class zeros : public range_facade
{
friend range_core_access;
struct impl
{
bool sentinel;
int current() const { return 0; }
void next() {}
bool equal(impl that) const
{ return sentinel == that.sentinel; }
};
// begin() и end() работают через range_facade
// как begin_impl и end_impl. И они будут одного типа
impl begin_impl() const { return {false}; }
impl end_impl() const { return {true}; }
};
// нули моделируют концепцию Range
CONCEPT_ASSERT(Range());
int main()
{
// бесконечность
for_each(zeros(), [](int i) {/*...*/});
}
I would like to immediately catch such errors, but, obviously, the binary function DenotesInfiniteSequence can not cope with this. For zeros, the BeginType and EndType types will be the same, so DenotesInfiniteSequence will return false.
Therefore, we need to construct a unary function of IsInfinite types that accepts an interval type.
// сообщить о том, будет ли Iterable бесконечным
template
struct is_infinite
: std::integral_constant
{};
It can be used to define the concept of FiniteIterable.
// текущий вариант синтаксиса Concept Lite
template
concept bool FiniteIterable =
Iterable && !is_infinite::value;
Each FiniteIterable is Iterable. A parallel hierarchy of refinements is observed:

And all these concepts, by analogy with Range, do not need to be defined in the code. Finiteness is orthogonal to the Iterable hierarchy, and can be interrogated separately.
But why FiniteIterable and not InfiniteIterable? It's all about the algorithms and their requirements. There are no algorithms that require their interval arguments to be infinite. Therefore, it would be useless to be able to write InfiniteIterable. But an algorithm like lower_bound would like the interval to be finite. From this and FiniteIterable.
So, all iterators model FiniteIterable by default, and the type must somehow learn to be infinite. How? It is possible to specialize is_infinite. Fortunately, tools for creating incrementors and intervals accept the optional IsInfinite parameter, so this is easy to do. Here's what the zeroes class now looks like:
// бесконечные нули
class zeros : public range_facade
{ // ... IsInfinite ...................^^^^
// ... тут всё, как было ...
};
// zeros – это Range, но он не Finite
CONCEPT_ASSERT(Range());
CONCEPT_ASSERT(!FiniteIterable());
By adding the FiniteIterable concept, we give algorithms that require finiteness the opportunity to verify this at the compilation stage.
Perhaps endless intervals
Now we need to divide the intervals into categories. In theory, either it is infinite or finite - is not it? No, actually. Take istream. It may be finite, it may not be. Usually the flow stops, but sometimes ...
The situation is complicated. Is it necessary to prohibit the transfer of istream to the algorithm only because it can be infinite?
Counting uncountable
At infinite intervals, there is such a difficulty: all iterators and all incrementors have a difference_type associated with them. Alexander Stepanov writes about this:
DistanceType returns an integer type large enough to measure any sequence of successor applications valid for the type.
It turns out that we need a whole type of infinite size. Is there a solution to this problem?
- In C ++, bigint is required - a whole type with infinite precision. In other languages it is. C ++ is a great language for creating libraries, and a library is just asking for it. If there was such a type, it could be taken as difference_type.
- Infinite intervals can use safe_int as difference_type. safe_int behaves like an int, but can represent infinity. It is not crowded. The two most difficult problems with difference_type overflows are undefined behavior and the inability to tell the fact what went wrong. With safe_int, uncertainties can be avoided and what happens later.
- An alternative safe_int implementation may be proposed in which it throws an exception on overflow.
- You could also see where the library uses difference_type and enable the user to specify that another type will be used there. For example, the distance calculation algorithm API may take an interval and an optional initial value. It would work by default with difference_type {0}, but if you passed bigint to it, you would work with it in a different, slower, but safer way.
- You can ignore the problem. And those who care about overflow can use the countdown interval adapter (https://github.com/ericniebler/range-v3/blob/master/include/range/v3/view/counted.hpp) to make sure that iterations will stop before difference_type overflows.
- Something else that didn’t occur to me.
Of course, I don’t like everything that slows down the operation of the algorithms, so std :: ptrdiff_t can be left as the difference_type by default. In addition, you need to design interval interfaces to give users the ability to set another difference_type if they care about overflow. Therefore, I like options 4 and 5. Other library types like bigint or safe_int with certain restrictions would be nice to be able to apply - if the user could specify their use, changing the speed to security when he needs it.
The result, and what to do next
Perhaps, while reading previous posts, you were overly optimistic: everything seemed to be starting to work out, and now you are confused. But it seems to me that we have made good progress in comparison with where we started. I described 5 problems with intervals using a pair of iterators. The new concept of incrementors solves 3 of them, the 4th problem (infinite intervals) can theoretically be solved by improving this concept. And there are several options for working with the 5th (overflow). At least a start has been made.
Some ask if I plan to get my ideas across to the C ++ standardization committee. Of course. When we get support for concepts in the language, there will be a need for a conceptualized version of STL, possibly working in a different namespace.
In the meantime, I will discuss the issue on the SG9 (Ranges) mailing list (http://www.open-std.org/mailman/listinfo/ranges). This controversial issue is likely to generate new ideas. Interested persons are encouraged to join the discussion.
The author brought his ideas to the committee and is now engaged in their implementation.
Other articles in the series
Intervals in C ++, Part 1: Intervals with delimiters
Intervals in C ++, Part 2: Infinite Intervals
Intervals in C ++, Part 3: Introducing Iterables
