Graphics in Julia. Strange patterns, the reflection of a triangle from a straight line and the construction of the normals of a spherical cat in a vacuum
- Tutorial

We continue to get acquainted with a very young, but incredibly beautiful and powerful programming language Julia . The six-year beta is finally over, so now you can not be afraid of changes in syntax. And while everyone is arguing, it’s good or bad to start indexing from one, the excited community has been actively messed up: new libraries are coming out, old ones are being updated, serious projects are being launched, and students are actively taught this language at universities. So let's not fall behind! Brew tea stronger, because this night we will code!
Preparation for work
There is a small overview in Russian, as well as on Habré there is an acquaintance with the language and installation guide . Again, I’m focusing on the need for the Windows Management Framework , there’s no problem with loading packages.
The JuliaPRO package after the update now includes only Juno . But personally, I prefer Jupyter : there were no problems with it on a laptop, plus it’s convenient to work in the browser and immediately create notes and formulas, in general, ideal for creating reports, slides or manuals.
- Скачиваем последнюю версию Юлии с официального сайта
- Ссылка на юпитер в комплекте Анаконды дана выше, я же использовал тот, что был в старой JuliaPRO
- Запускаем Julia. Уже можно полноценно пользоваться языком, но только в режиме интерпретатора. Выполняем команды:
julia>] pkg> add IJulia pkg> build IJulia # если не произошел автоматический build - Теперь в Jupyter доступно создание файла Julia 1.0.1
There are several packages for Julia, the most successful ones are included in Plots as backends. Plots.jl- metalanguage plotting: that is, an interface for various graph libraries. So it Plots.jlreally just interprets your commands, and then creates graphs using some kind of graph library. These background graphic libraries are called backends. The most pleasant thing is that you can use many different graphic libraries with syntax Plots.jl, and we will also see that it Plots.jladds new functions to each of these libraries!
Для установки пакетов выполните команды в REPL, Juno или Jupyter:
# Pkg.add("Plots") # так добавлили пакеты до версии 0.7.0
julia>]
pkg>add Plots
pkg>add GR
pkg>add PyPlot
pkg>add Gadfly
pkg>add PlotlyJS
pkg>add UnicodePlotsНе обязательно устанавливать все пакеты, но стоит знать, что у каждого из них есть свои особенности. Я предпочитаю plotlyjs(): хоть он и не отличается быстродействием, зато очень интерактивный. Есть зум, перемещение по плоскости, а также возможность сохранения файла, причем если сохранить документ Jupyter как html, все возможности сохранятся. Так что можно добавить на сайт или сделать интерактивную презентацию. Больше информации на страницах: Plots, Gadfly
Endless pattern based on prime numbers
Implemented the idea of an article on Habré . In a few words: what if we take the coordinate of a point and between an abscissa and ordinate, apply some operation, say, XOR or bitwise AND , and then check the number for simplicity or for belonging to Fibonacci numbers, and if the answer is positive, fill the point with one color, and with a negative in the other? Check:
using Plots
plotlyjs()
function eratosphen(n, lst) # решето Эратосфена
ar = [i for i=1:n]
ar[1] = 0
for i = 1:n
if ar[i] != 0
push!(lst, ar[i])
for j = i:i:n
ar[j] = 0
end
end
end
end
ertsfn = []
eratosphen(1000, ertsfn)
# print(ertsfn)
# print( size(ertsfn) ) # -> 168
N = 80
M = 80
W1 = [in( x % y, ertsfn) for x = 1:N, y = 1:M];
W2 = [x % y for x = 1:N, y = 1:M];
p1 = spy(W1, title = "x % y is prime?")
p2 = spy(W2, title = "x % y")
plot(p1, p2, layout=(2),legend=false)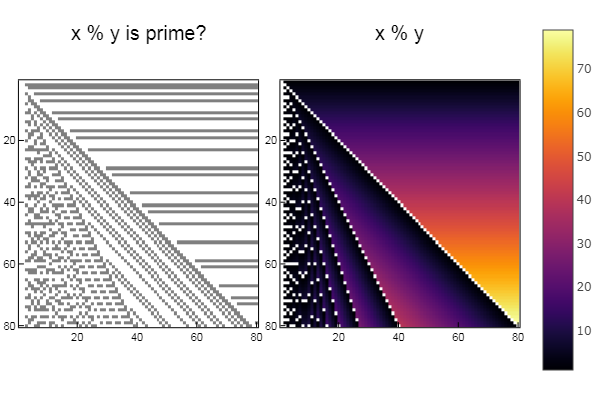
W1 = [in( x + y, ertsfn) for x = 1:N, y = 1:M];
W2 = [x + y for x = 1:N, y = 1:M];
p1 = spy(W1, title = "x + y is prime?")
p2 = spy(W2, title = "x + y")
plot(p1, p2, layout=(2),legend=false)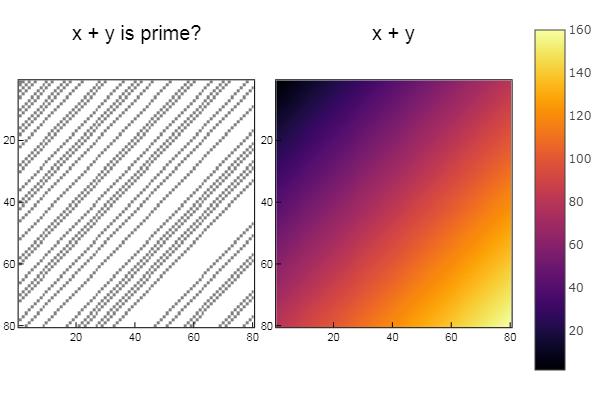
W1 = [in( x | y, ertsfn) for x = 1:N, y = 1:M];
W2 = [x | y for x = 1:N, y = 1:M];
p1 = spy(W1, title = "x | y is prime?")
p2 = spy(W2, title = "x | y")
plot(p1, p2, layout=(2),legend=false)
W1 = [in( x & y, ertsfn) for x = 1:N, y = 1:M];
W2 = [x & y for x = 1:N, y = 1:M];
p1 = spy(W1, title = "x & y is prime?")
p2 = spy(W2, title = "x & y")
plot(p1, p2, layout=(2),legend=false)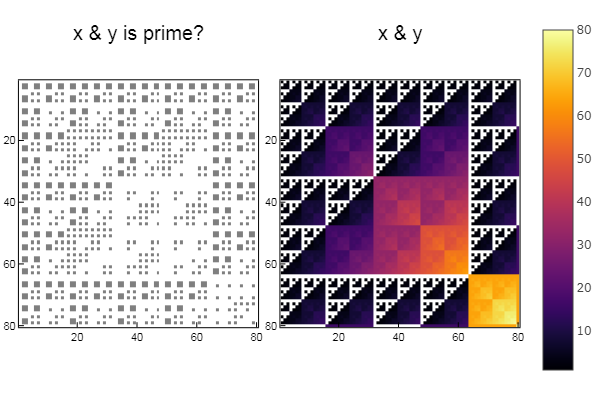
W1 = [in( xor(x, y), ertsfn) for x = 1:N, y = 1:M];
W2 = [xor(x, y) for x = 1:N, y = 1:M];
p1 = spy(W1, title = "x xor y is prime?")
p2 = spy(W2, title = "x xor y")
plot(p1, p2, layout=(2),legend=false)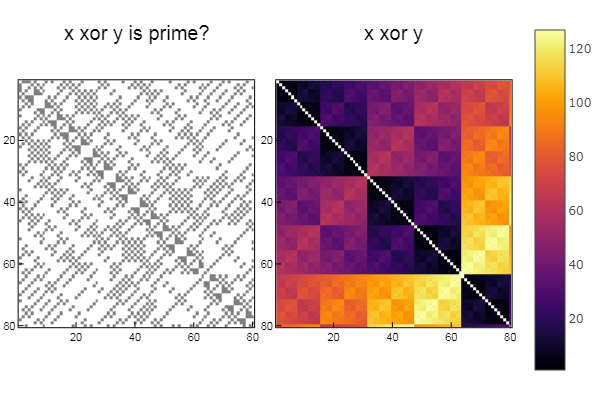
Можно как обычно составлять ряд чем-то вроде:
function fib(n)
a = 0
b = 1
for i = 1:n
a, b = b, a + b
end
return a
end
fbncc = fib.( [i for i=1:10] )Но воспользуемся-ка матричным представлением (подробнее):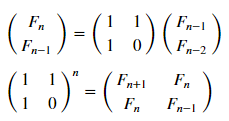
matr_fib = n -> [1 1; 1 0]^(n-1) # анонимная функция, возводящая матрицу в степень n-1
mfbnc = [ matr_fib( i )[1,1] for i=1:17]; # элемент 1,1 этой матрицы есть n-й элемент множества Фибоначчи
N = 100
M = N
W1 = [in( x % y, mfbnc) for x = 1:N, y = 1:M];
W2 = [in( x | y, mfbnc) for x = 1:N, y = 1:M];
p1 = spy(W1, title = "x % y ∈ fibonacci?")
p2 = spy(W2, title = "x | y ∈ fibonacci?")
plot(p1, p2, layout=(2),legend=false)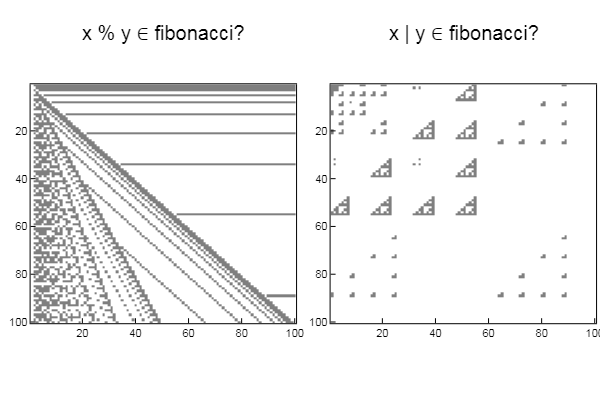
W1 = [in( xor(x, y), mfbnc) for x = 1:N, y = 1:M];
W2 = [in( x & y, mfbnc) for x = 1:N, y = 1:M];
p1 = spy(W1, title = "x xor y ∈ fibonacci?")
p2 = spy(W2, title = "x & y ∈ fibonacci?")
plot(p1, p2, layout=(2),legend=false)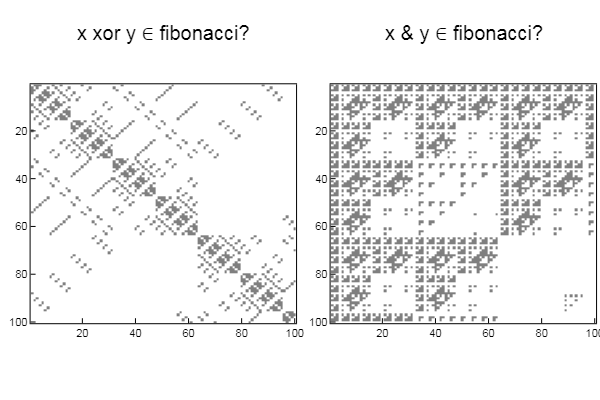
The reflection of the figure is relatively straightforward.
This type of display is determined by the matrix:
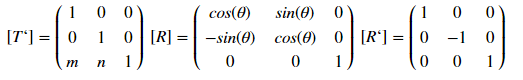
where [T '], [R] and [R'], respectively, of the matrix of displacement, rotation and reflection. How it works? Using an example of an offset, for a point with coordinates (x, y), the offset by m by ix and by n by the game will be determined by the transformation:
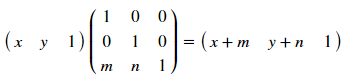
These matrices allow conversions for different polygons, the main thing is to write down the coordinates under each other and not forget about the column of ones at the end. Thus [T]:
- shifts the line at the origin along with the polygon to be transformed
- turns it to coincide with the X axis
- reflects all points of the polygon relative to X
- then reverse and translate
In more detail the topic is disclosed in the book of Rogers D., Adams J. Mathematical foundations of computer graphics
Now code it!
using Plots
plotlyjs()
f = x -> 0.4x + 2 # функция задающая прямую
# иксы и игреки транспонируем в столбцы
X = [2 4 2 2]'
Y = [4 6 6 4]'
xs = [-2; 7] # отрезок принадлежащий прямой
ys = f(xs)
inptmtrx = [ X Y ones( size(X, 1), 1 ) ] # приписываем столбец единиц
m = 0
n = -f(0) # смещение по Y
displacement = [1 0 0; 0 1 0; m n 1]
a = (ys[2]-ys[1]) / (xs[2]-xs[1]) # тангенс угла наклона прямой
θ = -atan(a)
rotation = [cos(θ) sin(θ) 0; -sin(θ) cos(θ) 0; 0 0 1]
reflection = [1 0 0; 0 -1 0; 0 0 1]
T = displacement * rotation * reflection * rotation^(-1) * displacement^(-1) # полная матрица преобразования
outptmtrx = inptmtrx * T
plot( X, Y)
plot!( xs, ys )
plot!( outptmtrx[:,1], outptmtrx[:,2] )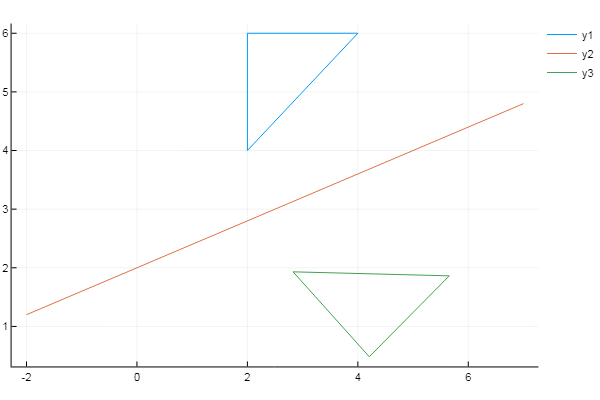
Interesting fact: if you get rid of the Greek characters and replace the first line with
function y=f(x,t)
y=0.4*x + 2
endfunction,brackets [] are framing indices of arrays on () , and rafts are on plot( X, Y, xs, ys, trianglenew(:,1), trianglenew(:,2) ), then this code is actually run in Scilab .
Work with three-dimensional graphics
Some of the listed packages support the construction of three-dimensional graphs. But separately I would like to mention Makie’s rather powerful visualization tool , which works in conjunction with the GLFW and GLAbstraction packages that implement the OpenGL features in julia. More information about Makie . His approbation hide under
using Makie
N = 51
x = linspace(-2, 2, N)
y = x
z = (-x .* exp.(-x .^ 2 .- (y') .^ 2)) .* 4
scene = wireframe(x, y, z)
xm, ym, zm = minimum(scene.limits[])
scene = surface!(scene, x, y, z)
contour!(scene, x, y, z, levels = 15, linewidth = 2, transformation = (:xy, zm))
scene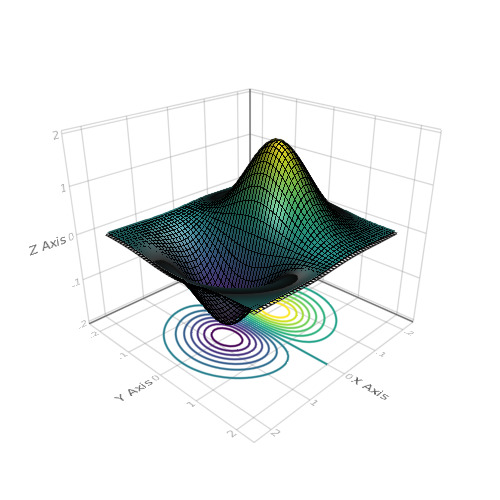
wireframe(Makie.loadasset("cat.obj"))
using FileIO
scene = Scene(resolution = (500, 500))
catmesh = FileIO.load(Makie.assetpath("cat.obj"), GLNormalUVMesh)
mesh(catmesh, color = Makie.loadasset("diffusemap.tga"))
x = Makie.loadasset("cat.obj")
mesh(x, color = :black)
pos = map(x.vertices, x.normals) do p, n
p => p .+ (normalize(n) .* 0.05f0)
end
linesegments!(pos, color = :blue)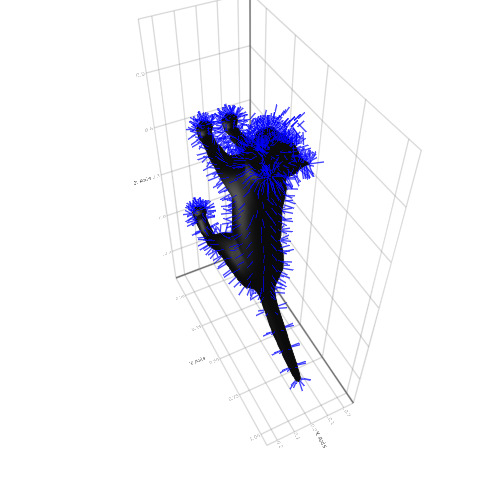
On this with all the graphics. Interactivity, animation, 3d, big data or fast construction of the simplest graphs - constantly evolving packages will satisfy almost every taste and need, moreover, everything is quite easy to master. Feel free to download practical tasks and continues to comprehend Julia!
UPD: All the above listings are made in Jupyter with julia 0.6.4. Unfortunately, some of the functions of the Plots metapacket were either removed or renamed, so that we continue to follow the updates, but in the meantime, the spy is completely replaced:
julia> using GR
julia> Z = [x | y for x = 1:40, y = 1:40];
julia> heatmap(Z)