Solution Management at SEBoK
- Transfer
Continuing the translation of SEBoK for the System Analysis course for undergraduates, he translated another section of SEBoK - Decision Management (in the original - Decision Management). This chapter includes more practical examples and is closer to reality than a description of the methods and principles of system analysis.
The chapter describes the decision making process based on multivariate analysis and promotes Value-Focused Thinking.
Systems engineering (systems engineering) includes many complex solutions, including many stakeholders, complex competing goals, a large share of uncertainty, and significant consequences.
In such a situation, good decision making requires a formalized decision management process. The purpose of the decision management process (ISO / IEC 15288: 2008):
Situations requiring a decision (opportunity) are usually encountered throughout the entire life cycle of the system. The decision management method is most often used by system engineers in evaluating alternatives. The study of alternatives is aimed at identifying, measuring and evaluating stakeholder requirements to facilitate the decision-maker finding the option that represents the best balance between competing goals.
Using the technique of decomposition of the considered solutions into logical parts and the subsequent synthesis of these parts back into a single whole, the decision management process allows the decision maker to work at a level understandable to a person, while avoiding unnecessary simplification of the problem.
In addition, by decomposing a common problem, experts can get an opportunity to evaluate alternative options within their subject area.
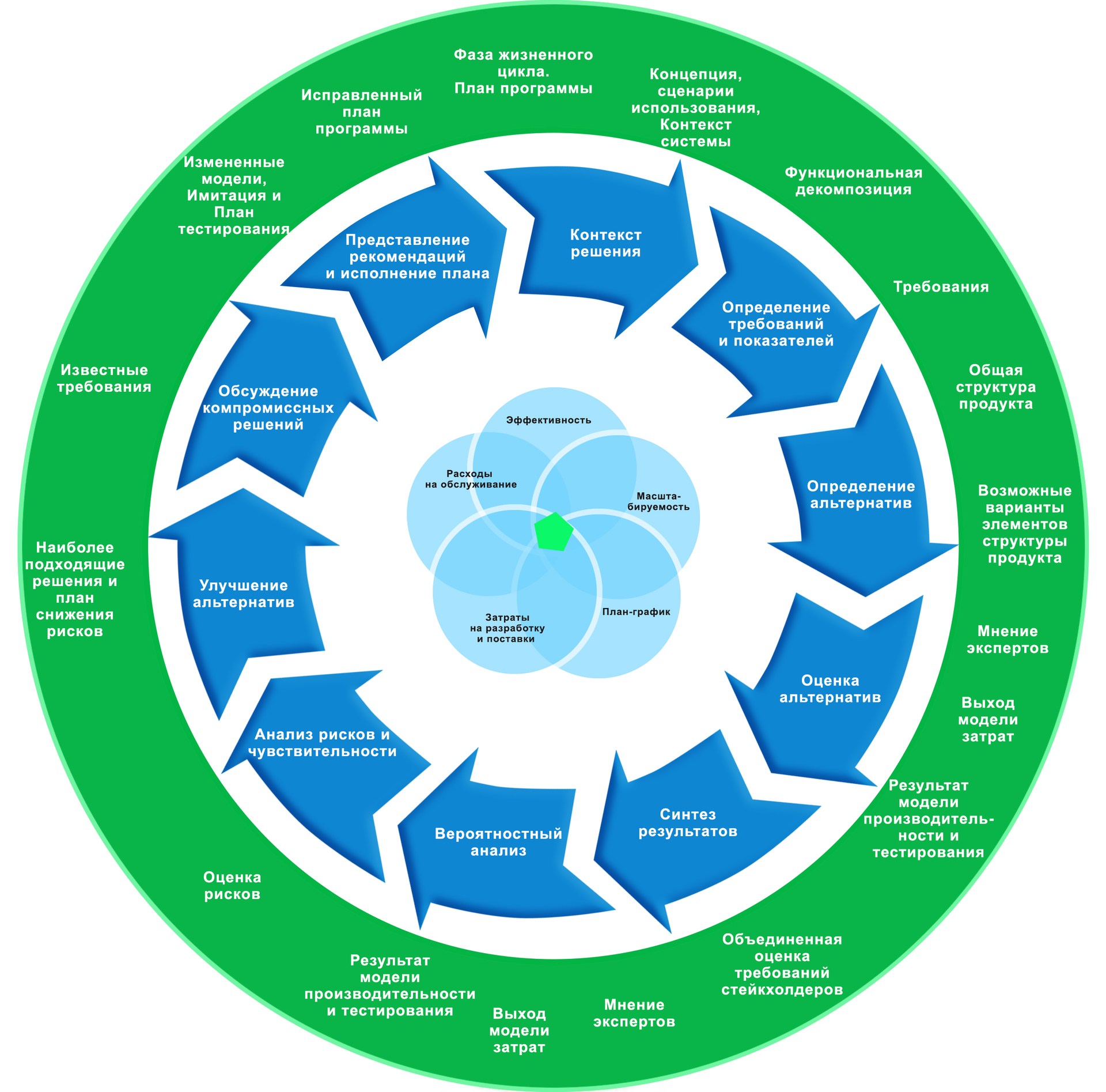
The decision analysis process is depicted in Figure 1 below. The decision management process is based on several “best practices”, including:
Five areas are shown in the center of the diagram (clockwise): productivity, growth potential (scalability), schedule, development and supply costs, and maintenance costs. Ten blue arrows represent the tasks of the decision-making process, and white text on a green background represents elements of the System Engineering process. The interaction is indicated by small dotted green or blue arrows.
The decision analysis process is repeated. To demonstrate each of the stages, the following sections describe the problem of creating UAVs ( note translation : this section will not address the requirements and goals of creating UAVs, only the direct process of comparison, therefore, for example, the distribution of the weights of indicators may look unreasonable) .
To ensure that the team fully understands the context of the solution, the analyst should describe the basic indicators, boundaries and interfaces of the system. The context of the decision includes: a description of the system, a life cycle stage, decision stages, a list of decision makers and stakeholders, available resources. It is best to determine the formulation of the decision-making problem in terms of the life cycle of the system.
Let's determine how difficult it is to make important decisions. Ralph Keeney (in 2002, professor of MIT):
Firstly, it is necessary to determine the requirements and indicators, using, for example, interviews and focus groups with domain experts (“expert”) and stakeholders. When evaluating alternatives in systems engineering, stakeholder values often include competing requirements in terms of performance, development schedule, cost, support costs, and development prospects. In corporations, the requirements of each shareholder should also be included in this list.
In terms of performance, functional decomposition will help you get a detailed set of potential goals. This list of core goals needs to be verified that each goal is truly important and controllable (manageable), and that the entire set is complete, not redundant, concise, specific, and understandable (Edwards et al. 2007). Figure 2 shows an example of a goal hierarchy.

Figure 2. Hierarchy of basic requirements (INCOSE DAWG 2013).
For each requirement, indicators must be defined to determine the value of each option in terms of this requirement. An indicator (property, evaluation criterion, and metric) must be unambiguous, comprehensive, consistent, valid, and understandable (Keeney & Gregory 2005).
The defining feature of multi-factor (multi-purpose) decision analysis is the transition from the space of indicators to the space of values. The transition is carried out using the evaluation function (value function, approx. Translation .: In our literature the term “function of desirability” is found ), which combines the scale of measurements with the range of evaluation.
When creating the evaluation function, the “walk-away point” on the indicator scale (x axis) should be set to 0 on the rating scale (y axis). A “failure point” is such a measurement result, in which, regardless of other results, the decision maker will refuse this decision. Measurement evaluation is also determined to the point where alternative options stop adding value, which is marked as an “achievable goal” (stretch goal, ideal). After that, a segment is marked up to 100 points (or 1, 10) on the rating scale (y axis).
Figure 3 shows the most common curves. The rationale for the form of the valuation function should be documented for tracking and protection.
The mathematics of multicriteria decision analysis requires that the weights depend on the importance of the metric and its range (from the “point of failure” to the ideal value). A useful tool for determining the priority of weights is the swing weight matrix. For each indicator, its importance is taken into account by determining whether it corresponds to the declared, critical or possible functions, taking into account the
gap between the existing implementation and the required one; as a result, the name of the measure is set in the corresponding matrix cell (Figure 4).
The highest priority metrics are placed in the upper left corner and have an unnormalized weight of 100. The unnormalized weight decreases to the lower right corner of the matrix. Weight fluctuation is estimated by comparing it with the most important measurement value or other measure. Weight is normalized to a total of one for the entire model used in the following sections.
Normalization is performed according to the formula:

Where:
To help create a creative and comprehensive set of alternative options covering the entire space of solutions, we consider the development of a table for creating alternatives (also known as a “morphological box”). This is the best method for establishing the semantic structure of the product for the system and for use in the presentation of the solution (Figure 5).
When goals and metrics are established and alternatives are identified, the problem solving team should hire subject experts with real data, test results, models and expert knowledge. Estimates are best recorded in the evaluation sheets for each alternative-metric combination, which describes the source of the assessment and the main reason (explanation). Figure 6 shows a set of ratings.
In addition to the alternatives found, the evaluation matrix includes a row for the perfect solution. An ideal is an instrument of goal-oriented thinking, which will be considered later.
Next, you can turn the measurements into a rating table using the evaluation function developed earlier. The color scheme can be useful for visualizing the values of trade-offs between different options and determining in which cases the options require development (Figure 7).
The final score for each alternative is calculated using the following formula:
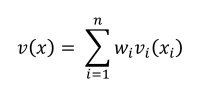
Where:
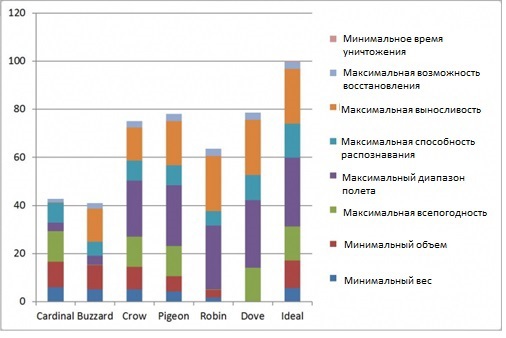
The chart of values by components (Figure 8) shows the overall score and the contribution of each weighted score to it for each option.
At the center of the process of managing systems engineering solutions is the analysis of alternatives, the ability to evaluate all requests (values) of stakeholders. The stakeholder value spreadsheet in Figure 9 shows 5 dimensions for each alternative:
Each alternative system is represented by a marker on the scatter diagram (Figure 9):
As part of the assessment, experts should discuss the possible uncertainty of the independent variables. Independent variables are variables that affect one or more score points; such estimates are called independent. Often, experts can evaluate high, acceptable, and low boundaries assuming low, medium, or high functionality. The Monte Carlo method, using these data, summarizes the influence of uncertainty and helps to determine the random variables that most affect the decision.
Determination of the influence of random variables - risk and sensitivity
analysis In the analysis of decisions, many forms of sensitivity analysis are used, including linear, “tornadoes”, “waterfalls” ( note translation: the name “bridge” is often used) diagrams and several methods for analyzing uncertainty, including the Monte Carlo Method, decision tree, and influence diagrams.
Line charts are used to demonstrate sensitivity to changes in weights. Figure 10 shows the results of applying the Monte Carlo Method for the analysis of functionality ratings.
The data obtained for the analysis of alternatives will most likely open up possibilities for modifying some decisions, declare previously unknown values, and / or reduce the risk. Using the initial conclusions to create new alternatives begins the process of transition of decision-making from “Variant-oriented thinking” to “Target-oriented thinking”.
This is the point in the process where the decision analysis team identifies key tradeoffs and the most important uncertainties and risks.
It is often useful to describe recommendations in the form of a clearly defined, specific list of tasks in order to increase the likelihood of a solution being implemented. Reports are important for tracking history and making decisions in the future.
Take the time and effort to create a comprehensive, high-quality report with a detailed description of the research results and their justification. Consider the possibility of expanding the static pages of a paper report with dynamic links in electronic form.
The chapter describes the decision making process based on multivariate analysis and promotes Value-Focused Thinking.
Systems engineering (systems engineering) includes many complex solutions, including many stakeholders, complex competing goals, a large share of uncertainty, and significant consequences.
In such a situation, good decision making requires a formalized decision management process. The purpose of the decision management process (ISO / IEC 15288: 2008):
“... provide a structured, analytical framework for identifying, describing and evaluating a set of alternative solutions at any point in the life cycle and choosing the most profitable line of business.”
Situations requiring a decision (opportunity) are usually encountered throughout the entire life cycle of the system. The decision management method is most often used by system engineers in evaluating alternatives. The study of alternatives is aimed at identifying, measuring and evaluating stakeholder requirements to facilitate the decision-maker finding the option that represents the best balance between competing goals.
Using the technique of decomposition of the considered solutions into logical parts and the subsequent synthesis of these parts back into a single whole, the decision management process allows the decision maker to work at a level understandable to a person, while avoiding unnecessary simplification of the problem.
In addition, by decomposing a common problem, experts can get an opportunity to evaluate alternative options within their subject area.
Decision Management Process
The decision analysis process is depicted in Figure 1 below. The decision management process is based on several “best practices”, including:
- Using mathematical methods of decision analysis to study alternatives. Parnell (2009).
- Development of one basic solution model (master model), with its subsequent refinement, updating and use as required for evaluating alternatives throughout the life cycle.
- Using Value-Focused Thinking (VFT) to get the best alternatives.
- Identification of uncertainties and risk assessment for each decision.
Five areas are shown in the center of the diagram (clockwise): productivity, growth potential (scalability), schedule, development and supply costs, and maintenance costs. Ten blue arrows represent the tasks of the decision-making process, and white text on a green background represents elements of the System Engineering process. The interaction is indicated by small dotted green or blue arrows.
The decision analysis process is repeated. To demonstrate each of the stages, the following sections describe the problem of creating UAVs ( note translation : this section will not address the requirements and goals of creating UAVs, only the direct process of comparison, therefore, for example, the distribution of the weights of indicators may look unreasonable) .
Constraint and adaptation of decisions (decision context)
To ensure that the team fully understands the context of the solution, the analyst should describe the basic indicators, boundaries and interfaces of the system. The context of the decision includes: a description of the system, a life cycle stage, decision stages, a list of decision makers and stakeholders, available resources. It is best to determine the formulation of the decision-making problem in terms of the life cycle of the system.
Development of requirements and indicators
Let's determine how difficult it is to make important decisions. Ralph Keeney (in 2002, professor of MIT):
“The most important decisions have multiple goals, and usually with multi-purpose solutions you cannot achieve all of them. You will be forced to accept less fulfillment of some requirements in order to fulfill others more. But how much less will you agree to achieve how much more? ”
Firstly, it is necessary to determine the requirements and indicators, using, for example, interviews and focus groups with domain experts (“expert”) and stakeholders. When evaluating alternatives in systems engineering, stakeholder values often include competing requirements in terms of performance, development schedule, cost, support costs, and development prospects. In corporations, the requirements of each shareholder should also be included in this list.
In terms of performance, functional decomposition will help you get a detailed set of potential goals. This list of core goals needs to be verified that each goal is truly important and controllable (manageable), and that the entire set is complete, not redundant, concise, specific, and understandable (Edwards et al. 2007). Figure 2 shows an example of a goal hierarchy.

Figure 2. Hierarchy of basic requirements (INCOSE DAWG 2013).
For each requirement, indicators must be defined to determine the value of each option in terms of this requirement. An indicator (property, evaluation criterion, and metric) must be unambiguous, comprehensive, consistent, valid, and understandable (Keeney & Gregory 2005).
The defining feature of multi-factor (multi-purpose) decision analysis is the transition from the space of indicators to the space of values. The transition is carried out using the evaluation function (value function, approx. Translation .: In our literature the term “function of desirability” is found ), which combines the scale of measurements with the range of evaluation.
When creating the evaluation function, the “walk-away point” on the indicator scale (x axis) should be set to 0 on the rating scale (y axis). A “failure point” is such a measurement result, in which, regardless of other results, the decision maker will refuse this decision. Measurement evaluation is also determined to the point where alternative options stop adding value, which is marked as an “achievable goal” (stretch goal, ideal). After that, a segment is marked up to 100 points (or 1, 10) on the rating scale (y axis).
Figure 3 shows the most common curves. The rationale for the form of the valuation function should be documented for tracking and protection.
Figure 3. Examples of evaluation function (INCOSE DAWG 2013)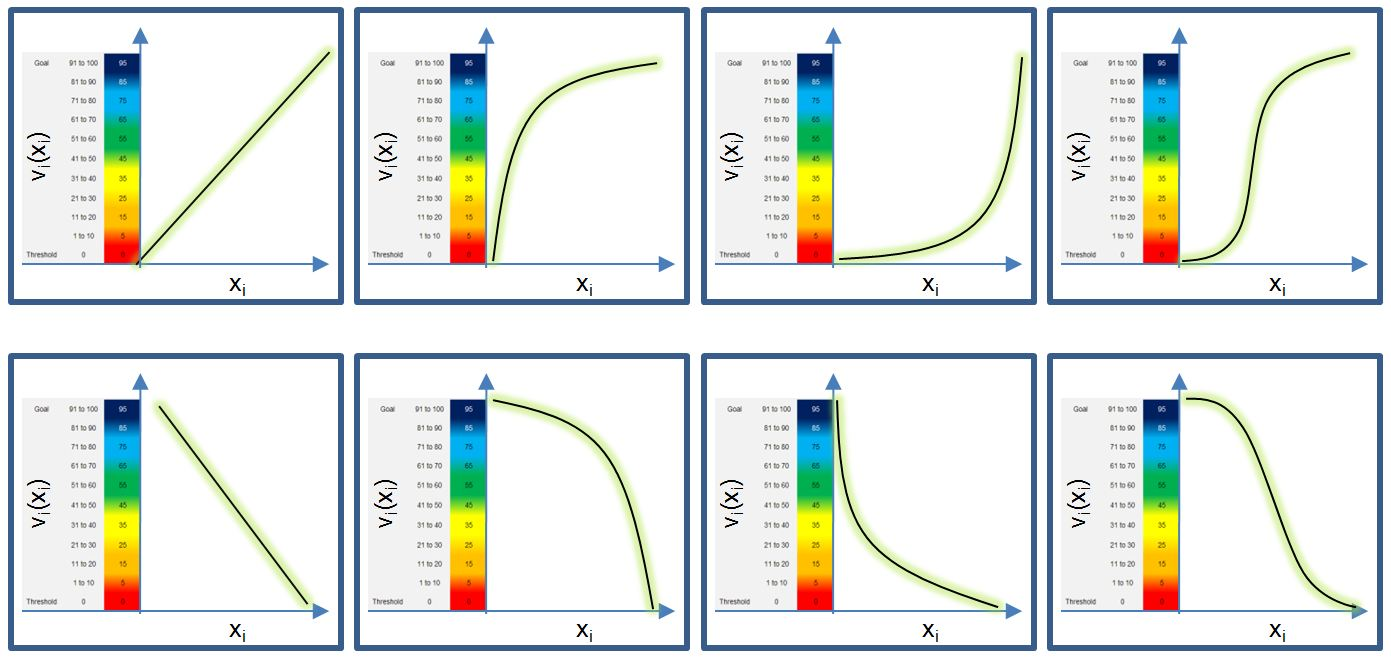
Figure 3. Examples of evaluation function (INCOSE DAWG 2013).

Figure 3. Examples of evaluation function (INCOSE DAWG 2013).
The mathematics of multicriteria decision analysis requires that the weights depend on the importance of the metric and its range (from the “point of failure” to the ideal value). A useful tool for determining the priority of weights is the swing weight matrix. For each indicator, its importance is taken into account by determining whether it corresponds to the declared, critical or possible functions, taking into account the
gap between the existing implementation and the required one; as a result, the name of the measure is set in the corresponding matrix cell (Figure 4).
The highest priority metrics are placed in the upper left corner and have an unnormalized weight of 100. The unnormalized weight decreases to the lower right corner of the matrix. Weight fluctuation is estimated by comparing it with the most important measurement value or other measure. Weight is normalized to a total of one for the entire model used in the following sections.
Normalization is performed according to the formula:
Where:
- w_i - indicator weight (normalized);
- f_i is the abnormalized weight of the indicator.
Figure 4. Weight fluctuation matrix (INCOSE DAWG 2013)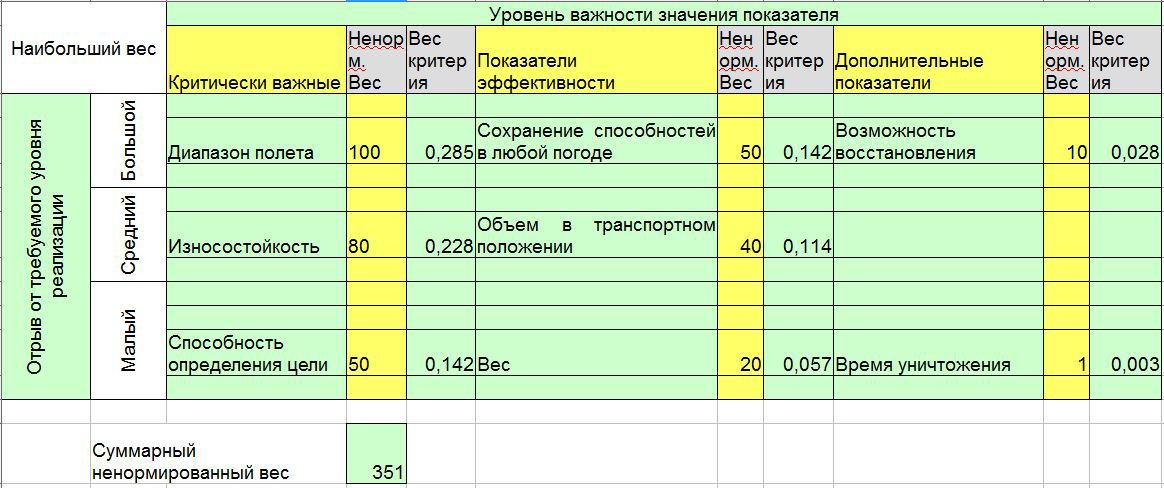
Creating alternatives
To help create a creative and comprehensive set of alternative options covering the entire space of solutions, we consider the development of a table for creating alternatives (also known as a “morphological box”). This is the best method for establishing the semantic structure of the product for the system and for use in the presentation of the solution (Figure 5).
Figure 5. Description of alternatives (INCOSE DAWG 2013).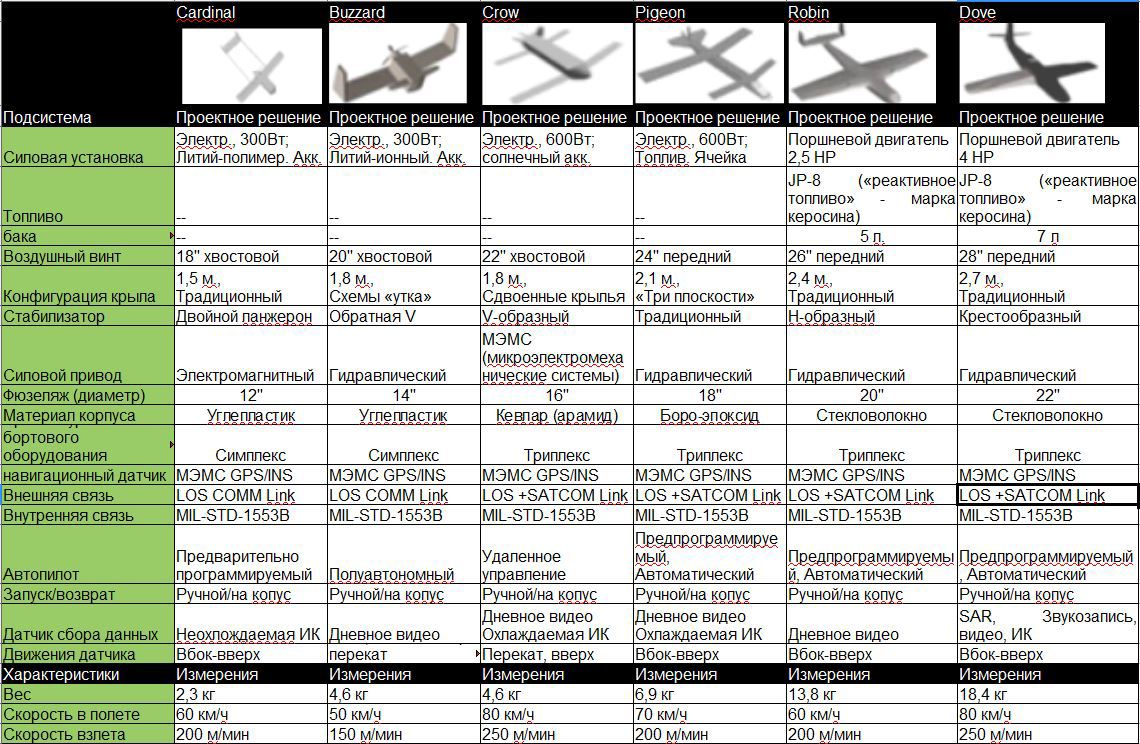
Assessment of alternatives using deterministic (factor) analysis
When goals and metrics are established and alternatives are identified, the problem solving team should hire subject experts with real data, test results, models and expert knowledge. Estimates are best recorded in the evaluation sheets for each alternative-metric combination, which describes the source of the assessment and the main reason (explanation). Figure 6 shows a set of ratings.
Figure 6. Measuring Alternatives (INCOSE DAWG 2013)
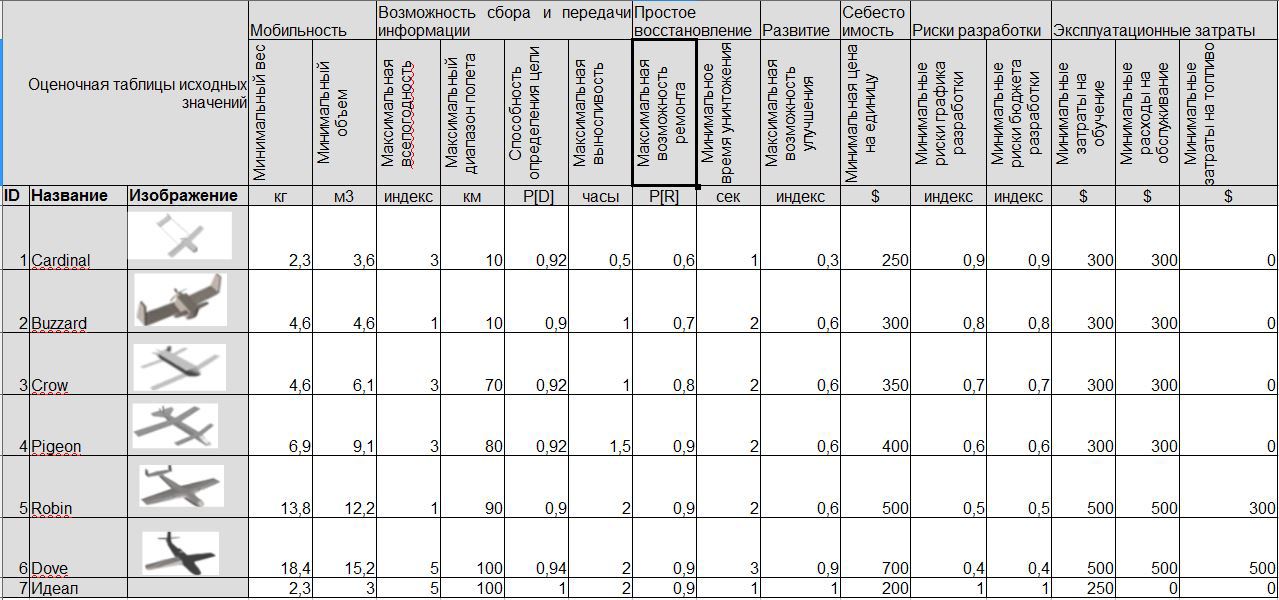
In addition to the alternatives found, the evaluation matrix includes a row for the perfect solution. An ideal is an instrument of goal-oriented thinking, which will be considered later.
Synthesis of Results
Next, you can turn the measurements into a rating table using the evaluation function developed earlier. The color scheme can be useful for visualizing the values of trade-offs between different options and determining in which cases the options require development (Figure 7).
Figure 7. Values of indicators from the color map (INCOSE DAWG 2013)
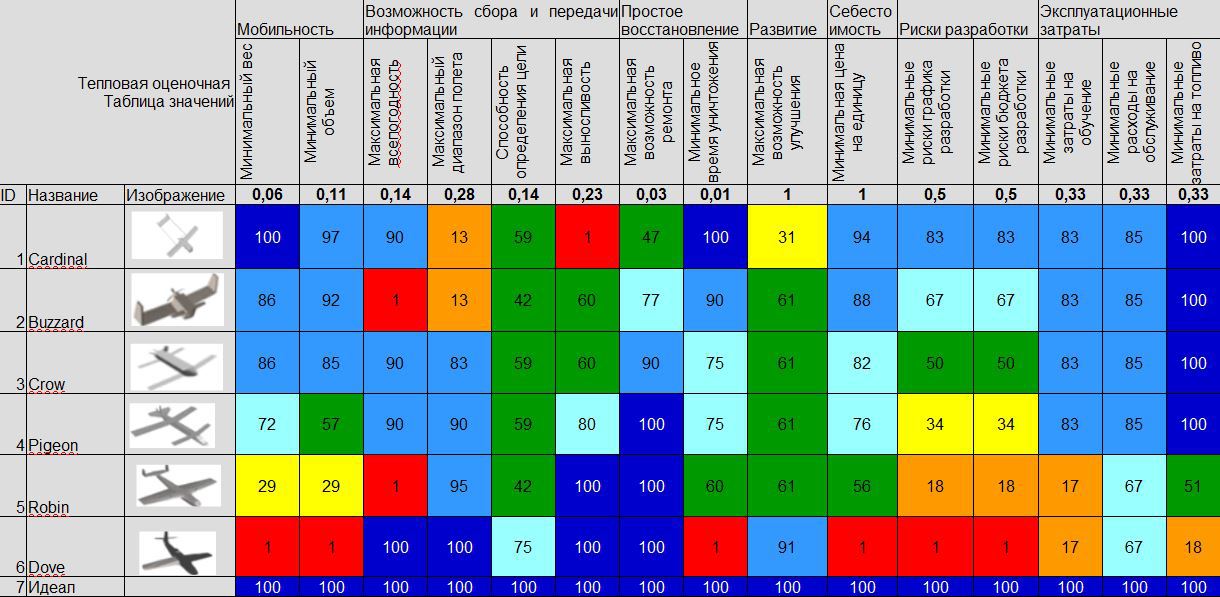
The final score for each alternative is calculated using the following formula:
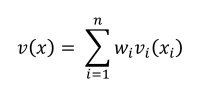
Where:
- V (x) - evaluation of the alternative;
- i = 1 to n is the number of metrics (criteria);
- xi is the value of the alternative according to the ith criterion;
- vi (xi) is the value of the estimate xi (one-dimensional estimate).
- wi is the weight of the Іth criterion.
- The sum of all wi is 1:
.
The chart of values by components (Figure 8) shows the overall score and the contribution of each weighted score to it for each option.
Figure 8. Chart of values by component (INCOSE DAWG 2013)

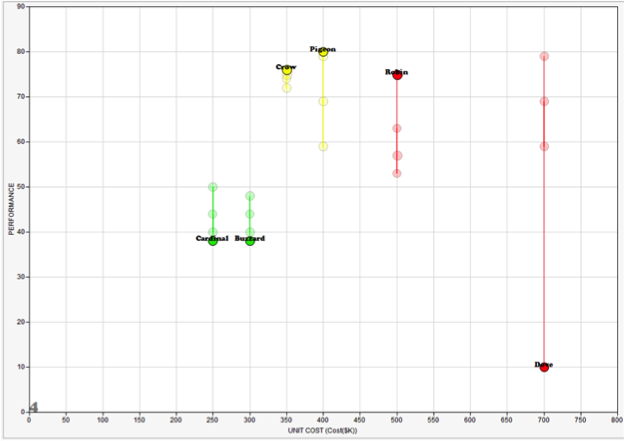
At the center of the process of managing systems engineering solutions is the analysis of alternatives, the ability to evaluate all requests (values) of stakeholders. The stakeholder value spreadsheet in Figure 9 shows 5 dimensions for each alternative:
- Cost price;
- Functionality;
- Implementation risk;
- Development prospects;
- Operating and maintenance costs.
Figure 9. An example of a stakeholder value scatter chart (INCOSE DAWG 2013).


Each alternative system is represented by a marker on the scatter diagram (Figure 9):
- Cost and functionality are laid off along the X and Y axes.
- The risk of implementation is indicated by the color of the marker (green = low, yellow = medium, red = high).
- Prospects for development are displayed as the number of “hats” above the corresponding marker (1 “hat” = low, 2 = medium, 3 = high).
Uncertainty identification and probabilistic analysis
As part of the assessment, experts should discuss the possible uncertainty of the independent variables. Independent variables are variables that affect one or more score points; such estimates are called independent. Often, experts can evaluate high, acceptable, and low boundaries assuming low, medium, or high functionality. The Monte Carlo method, using these data, summarizes the influence of uncertainty and helps to determine the random variables that most affect the decision.
Determination of the influence of random variables - risk and sensitivity
analysis In the analysis of decisions, many forms of sensitivity analysis are used, including linear, “tornadoes”, “waterfalls” ( note translation: the name “bridge” is often used) diagrams and several methods for analyzing uncertainty, including the Monte Carlo Method, decision tree, and influence diagrams.
Line charts are used to demonstrate sensitivity to changes in weights. Figure 10 shows the results of applying the Monte Carlo Method for the analysis of functionality ratings.
Figure 10. Uncertainty in functionality based on the Monte Carlo method (INCOSE DAWG 2013).

Development of alternatives
The data obtained for the analysis of alternatives will most likely open up possibilities for modifying some decisions, declare previously unknown values, and / or reduce the risk. Using the initial conclusions to create new alternatives begins the process of transition of decision-making from “Variant-oriented thinking” to “Target-oriented thinking”.
Compromise discussion
This is the point in the process where the decision analysis team identifies key tradeoffs and the most important uncertainties and risks.
Submission of recommendations and implementation of the action plan
It is often useful to describe recommendations in the form of a clearly defined, specific list of tasks in order to increase the likelihood of a solution being implemented. Reports are important for tracking history and making decisions in the future.
Take the time and effort to create a comprehensive, high-quality report with a detailed description of the research results and their justification. Consider the possibility of expanding the static pages of a paper report with dynamic links in electronic form.