Social Network Analysis: Spark GraphX
Hi, Habr!
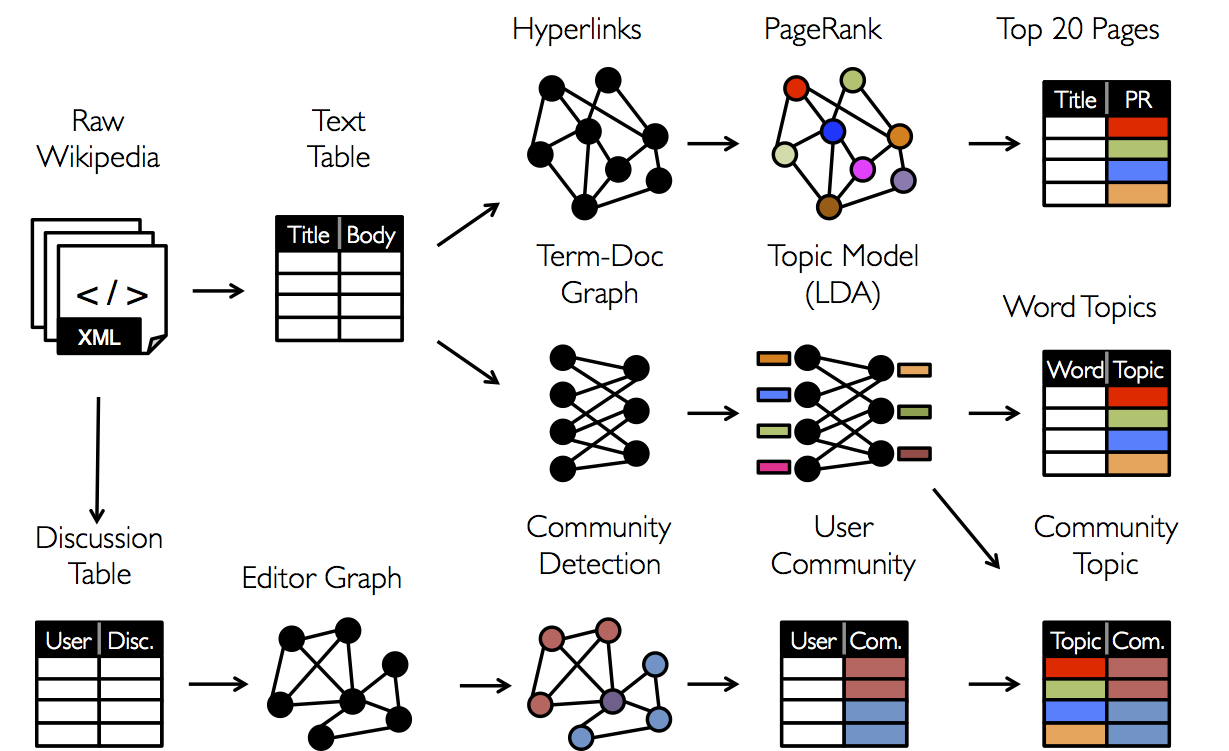
Today we will take a closer look at the tasks of Social Networking Analysis ( SNA ), as well as end the review of the Apache Spark library designed for Big Data analysis. Namely, as promised in previous articles ( one and two ), we will consider one of the Apache Spark components intended for graph analysis - GraphX . We will try to understand how distributed storage of graphs and calculations on them is implemented in this library. And also we will show with specific examples how this library can be used in practice: spam search, search engine ranking, highlighting communities on social networks, search for opinion leaders - this is not a complete list of applications of graph analysis methods.
So, let's start by recalling (for those who are not immersed in graph theory) the main objects that we will work with in this article and dive into the algorithms and all the beautiful mathematics that are behind this.
Probably the best thing in this section is to send the reader to watch wonderful video lectures and brochures by my scientific adviser Andrei Mikhailovich Raigorodsky , for example, here - no one can tell you this better and more clearly about him. It is highly recommended that you also look at this or that . Better yet, sign up for Andrei Mikhailovich's course at Coursera . Therefore, here we will only give basic concepts and will not go into details.
A graph is a pair of G = (V, E) - where, V is the set of vertices (say, sites on the Internet), and E is the set of edgesconnecting vertices (respectively, links between sites). An understandable structure that has been analyzed for many years. However, in practice, when analyzing real networks, the question arises - how is this graph constructed? Let's say a new site appears on the Internet - to whom will it link in the first place, how many new links will appear on average, how well will this site rank in search results?
This problem (the device of the web graph ) people have been dealing with almost since the advent of the Internet. During this time, many models were invented . Not so long ago , a generalized model was proposed in Yandex , and its properties were also investigated .
If the graph is already given to us, its properties, as well as further calculations on the graph, are well defined. For example, you can examine the degree of a particular vertex as yourself (the number of friends of a person on a social network), or measure the distance between specific peaks (how many handshakes 2 given people know in a network), calculate the components of connectivity (a group of people where, according to the “connections” between people any 2 people are familiar) and much more.
The classic algorithms are:
PageRank - a well-known algorithm for calculating the “authority” of a vertex in a graph, proposed by Google in 1998 and has long been used to rank search results.
Search for (strongly) connected components- an algorithm for searching subsets of vertices of a graph such that there exists a path between any two vertices from a particular subset, and there are no paths between the vertices of different subsets
Counting the shortest paths in a graph - between any pair of vertices, between specific two vertices, on weighted graphs and in other settings
As well as counting the number of triangles, clustering, distribution of degrees of vertices, search for clicks in a graph, and much more. It is worth noting that most of the algorithms are iterative, and therefore, in this context, the GraphX library shows itself very well due to the fact that it caches data in RAM. Next, we will consider what opportunities this library provides us.
Just note that GraphX is far from the first and not the only graph analysis tool (known tools are, for example, GraphLab - the current Dato.com or the Pregel calculation model - the API of which is partially used in GraphX), as well as the fact that at the moment The writing of this post the library was still in development and its capabilities are not so great. Nevertheless, for almost any tasks that arise in practice GraphX justifies its application in one way or another.
GraphX does not yet support Python, so the code will be written in Scala, assuming that SparkContext has already been created (in the code below, the variable sc) Most of the code below is taken from documentation and open source materials. So, for starters, download all the necessary libraries:
In spark, the concept of the graph is implemented in the form of the so-called Property Graph - this is a multigraph with labels (additional information) on the vertices and edges. A multigraph is a directed (edges have directions) graph in which multiple edges are allowed (there may be several edges between two vertices), loops (an edge from a vertex to itself). Immediately, we say that in the case of oriented graphs, concepts such as the incoming degree (the number of incoming edges) and the outgoing degree (the number of edges originating from the vertex) are defined . Let's look at examples of how you can build a specific graph.
You can build a graph using the Graph constructor , passing in the arrays of vertices and edges from the local program (not forgetting to make them RDD using the .parallelize () function ):
Or, if the vertices and edges must first be built on the basis of some data lying, say in HDFS , you must first process the original data itself (as is often the case with .map () conversion). For example, if we have Wikipedia articles stored as (id, title) , as well as links between articles stored as pairs, then the graph is built quite easily - to do this, separate id from title in the first case and construct the edges themselves (there is an Edge constructor for this ) - in the second case, upon output, we get a list of vertices and edges that can be passed to the Graph constructor :
After constructing a graph for it, you can calculate some characteristics and also run algorithms on it, including those listed above. Until we continue, it is worth noting here that in addition to the concept of vertices and edges, the concept of triplet ( Triplet ) is also implemented - this is an object that, in a sense, slightly extends the object edge ( Edge ) - it also contains information about the edge about the peaks adjacent to it.
The remarkable fact is that in most packages (and GraphX is no exception) - after building a graph, it becomes easy to do calculations on it and also run standard algorithms. Indeed, the methods of calculation on graphs themselves have been studied quite well, and in specific applications, the most difficult thing is to determine the graph, namely, to determine what are vertices and what are edges (on what basis should they be drawn). Below is a list of some of the available methods for the Graph object with comments:
It is worth noting that in the current implementation of SparkX contains quite a few implemented algorithms, therefore, it is still relevant to use the above known packages instead of Apache Spark, however, there is confidence that GraphX will be significantly improved in the future, and due to the possibility of caching data in RAM, probably gain enough popularity in graph problems. In conclusion, we give examples of practical problems where graph methods have to be applied.
As mentioned above - the main problem in practical problems is no longer to run complex algorithms - namely, the correct definition of the graph, its proper preprocessing and reducing the problem to a classical solved one. Consider this by way of examples, where we leave the reader a large number of questions for reflection:
Prediction of the appearance of a new rib (Link Prediction)
The problem is quite common - given a sequence of edges that are added to the graph until some point. It is necessary to predict which edges will appear in the future in our graph. From the point of view of real life, this task is part of a recommender system - for example, forecasting connections (“friendships”) between two social users. network. In this problem, in fact, for each pair of arbitrarily selected vertices it is necessary to predict - what is the probability that there will be an edge between them in the future - here you just need to work with the characteristics and with the description of the vertices. For example, as one of the signs may be the intersection of sets of friends, or Jacquard measure. The reader is invited to think about possible metrics of similarity between vertices and write his own variation in the comments).
Allocation of communities in social networks
A task that is difficult to attribute to any specific tasks. Often, it is considered in the context of the task of "clustering on graphs." There are a lot of methods for solving this problem, from simple extraction of connected components (the algorithm was mentioned above) with a correctly defined subset of vertices, to sequential removal of edges from the graph until the desired component remains. Here, again - it is very important to first understand which communities we want to highlight on the network, i.e. first work with a description of the vertices and edges, and only then think about how to distinguish the communities themselves in the resulting subgraph.
Shortest graph distances
This task is also classical and is implemented, for example, in the same Yandex.Metro or other services that help find the shortest paths in a certain graph - whether it is a graph of connections between points of a city or a graph of acquaintances.
Or a task that a mobile operator, for example, can easily face:
Determining opinion leaders on the network
To promote, say, a new option, for example, the mobile Internet, in order to optimize the advertising budget, I would like to single out people who are in some ways surrounded by attention from . In our terms, these are the vertices of the graph that have great authority on the network - therefore, this task with the correct construction of the graph reduces to the PageRank problem.
So, we examined typical applied problems of graph analysis that may arise in practice, as well as one of the tools that can be used to solve them. This concludes the review of the Apache Spark library, and indeed the overview of tools, and in the future we will focus more on algorithms and specific tasks!

Today we will take a closer look at the tasks of Social Networking Analysis ( SNA ), as well as end the review of the Apache Spark library designed for Big Data analysis. Namely, as promised in previous articles ( one and two ), we will consider one of the Apache Spark components intended for graph analysis - GraphX . We will try to understand how distributed storage of graphs and calculations on them is implemented in this library. And also we will show with specific examples how this library can be used in practice: spam search, search engine ranking, highlighting communities on social networks, search for opinion leaders - this is not a complete list of applications of graph analysis methods.
So, let's start by recalling (for those who are not immersed in graph theory) the main objects that we will work with in this article and dive into the algorithms and all the beautiful mathematics that are behind this.
Graph Theory, Random and Web Graphs
Probably the best thing in this section is to send the reader to watch wonderful video lectures and brochures by my scientific adviser Andrei Mikhailovich Raigorodsky , for example, here - no one can tell you this better and more clearly about him. It is highly recommended that you also look at this or that . Better yet, sign up for Andrei Mikhailovich's course at Coursera . Therefore, here we will only give basic concepts and will not go into details.
A graph is a pair of G = (V, E) - where, V is the set of vertices (say, sites on the Internet), and E is the set of edgesconnecting vertices (respectively, links between sites). An understandable structure that has been analyzed for many years. However, in practice, when analyzing real networks, the question arises - how is this graph constructed? Let's say a new site appears on the Internet - to whom will it link in the first place, how many new links will appear on average, how well will this site rank in search results?
This problem (the device of the web graph ) people have been dealing with almost since the advent of the Internet. During this time, many models were invented . Not so long ago , a generalized model was proposed in Yandex , and its properties were also investigated .
If the graph is already given to us, its properties, as well as further calculations on the graph, are well defined. For example, you can examine the degree of a particular vertex as yourself (the number of friends of a person on a social network), or measure the distance between specific peaks (how many handshakes 2 given people know in a network), calculate the components of connectivity (a group of people where, according to the “connections” between people any 2 people are familiar) and much more.
The classic algorithms are:
PageRank - a well-known algorithm for calculating the “authority” of a vertex in a graph, proposed by Google in 1998 and has long been used to rank search results.
Search for (strongly) connected components- an algorithm for searching subsets of vertices of a graph such that there exists a path between any two vertices from a particular subset, and there are no paths between the vertices of different subsets
Counting the shortest paths in a graph - between any pair of vertices, between specific two vertices, on weighted graphs and in other settings
As well as counting the number of triangles, clustering, distribution of degrees of vertices, search for clicks in a graph, and much more. It is worth noting that most of the algorithms are iterative, and therefore, in this context, the GraphX library shows itself very well due to the fact that it caches data in RAM. Next, we will consider what opportunities this library provides us.
Spark graphx
Just note that GraphX is far from the first and not the only graph analysis tool (known tools are, for example, GraphLab - the current Dato.com or the Pregel calculation model - the API of which is partially used in GraphX), as well as the fact that at the moment The writing of this post the library was still in development and its capabilities are not so great. Nevertheless, for almost any tasks that arise in practice GraphX justifies its application in one way or another.
GraphX does not yet support Python, so the code will be written in Scala, assuming that SparkContext has already been created (in the code below, the variable sc) Most of the code below is taken from documentation and open source materials. So, for starters, download all the necessary libraries:
import org.apache.spark.graphx._
import org.apache.spark.rdd.RDD
In spark, the concept of the graph is implemented in the form of the so-called Property Graph - this is a multigraph with labels (additional information) on the vertices and edges. A multigraph is a directed (edges have directions) graph in which multiple edges are allowed (there may be several edges between two vertices), loops (an edge from a vertex to itself). Immediately, we say that in the case of oriented graphs, concepts such as the incoming degree (the number of incoming edges) and the outgoing degree (the number of edges originating from the vertex) are defined . Let's look at examples of how you can build a specific graph.
Graph construction
You can build a graph using the Graph constructor , passing in the arrays of vertices and edges from the local program (not forgetting to make them RDD using the .parallelize () function ):
val vertexArray = Array(
(1L, ("Alice", 28)),
(2L, ("Bob", 27)),
(3L, ("Charlie", 65)),
(4L, ("David", 42)),
(5L, ("Ed", 55)),
(6L, ("Fran", 50))
)
val edgeArray = Array(
Edge(2L, 1L, 7),
Edge(2L, 4L, 2),
Edge(3L, 2L, 4),
Edge(3L, 6L, 3),
Edge(4L, 1L, 1),
Edge(5L, 2L, 2),
Edge(5L, 3L, 8),
Edge(5L, 6L, 3)
)
val vertexRDD = sc.parallelize(vertexArray)
val edgeRDD = sc.parallelize(edgeArray)
val graph = Graph(vertexRDD, edgeRDD)
Or, if the vertices and edges must first be built on the basis of some data lying, say in HDFS , you must first process the original data itself (as is often the case with .map () conversion). For example, if we have Wikipedia articles stored as (id, title) , as well as links between articles stored as pairs, then the graph is built quite easily - to do this, separate id from title in the first case and construct the edges themselves (there is an Edge constructor for this ) - in the second case, upon output, we get a list of vertices and edges that can be passed to the Graph constructor :
val articles = sc.textFile("articles.txt")
val links = sc.textFile("links.txt")
val vertices = articles.map { line =>
val fields = line.split('\t')
(fields(0).toLong, fields(1))
}
val edges = links.map { line =>
val fields = line.split('\t')
Edge(fields(0).toLong, fields(1).toLong, 0)
}
val graph = Graph(vertices, edges, "").cache()
After constructing a graph for it, you can calculate some characteristics and also run algorithms on it, including those listed above. Until we continue, it is worth noting here that in addition to the concept of vertices and edges, the concept of triplet ( Triplet ) is also implemented - this is an object that, in a sense, slightly extends the object edge ( Edge ) - it also contains information about the edge about the peaks adjacent to it.
Graph Calculations
The remarkable fact is that in most packages (and GraphX is no exception) - after building a graph, it becomes easy to do calculations on it and also run standard algorithms. Indeed, the methods of calculation on graphs themselves have been studied quite well, and in specific applications, the most difficult thing is to determine the graph, namely, to determine what are vertices and what are edges (on what basis should they be drawn). Below is a list of some of the available methods for the Graph object with comments:
class Graph[VD, ED] {
// Базовые статистики графа
val numEdges: Long // количество ребер
val numVertices: Long // количество вершин
val inDegrees: VertexRDD[Int] // входящие степени вершин
val outDegrees: VertexRDD[Int] // исходящие степени вершин
val degrees: VertexRDD[Int] // суммарные степени вершин
// Отдельные представления вершин, ребер и триплетов
val vertices: VertexRDD[VD]
val edges: EdgeRDD[ED]
val triplets: RDD[EdgeTriplet[VD, ED]]
// Изменение атрибутов (дополнительной информации) у вершин и ребер
def mapVertices[VD2](map: (VertexID, VD) => VD2): Graph[VD2, ED]
def mapEdges[ED2](map: Edge[ED] => ED2): Graph[VD, ED2]
def mapEdges[ED2](map: (PartitionID, Iterator[Edge[ED]]) => Iterator[ED2]): Graph[VD, ED2]
def mapTriplets[ED2](map: EdgeTriplet[VD, ED] => ED2): Graph[VD, ED2]
// Модификации графов
def reverse: Graph[VD, ED] // обращение - все ребра меняют направление на противоположное
def subgraph(
epred: EdgeTriplet[VD,ED] => Boolean = (x => true),
vpred: (VertexID, VD) => Boolean = ((v, d) => true))
: Graph[VD, ED] // выделение подграфов, удовлетворяющих определенным условиям
def groupEdges(merge: (ED, ED) => ED): Graph[VD, ED] // слияние ребер
// Базовые графовые алгоритмы
def pageRank(tol: Double, resetProb: Double = 0.15): Graph[Double, Double] // вычисление PageRank
def connectedComponents(): Graph[VertexID, ED] // поиск компонент связности
def triangleCount(): Graph[Int, ED] // подсчет числа треугольников
def stronglyConnectedComponents(numIter: Int): Graph[VertexID, ED] // поиск сильных компонент связности
}
It is worth noting that in the current implementation of SparkX contains quite a few implemented algorithms, therefore, it is still relevant to use the above known packages instead of Apache Spark, however, there is confidence that GraphX will be significantly improved in the future, and due to the possibility of caching data in RAM, probably gain enough popularity in graph problems. In conclusion, we give examples of practical problems where graph methods have to be applied.
Practical tasks
As mentioned above - the main problem in practical problems is no longer to run complex algorithms - namely, the correct definition of the graph, its proper preprocessing and reducing the problem to a classical solved one. Consider this by way of examples, where we leave the reader a large number of questions for reflection:
Prediction of the appearance of a new rib (Link Prediction)
The problem is quite common - given a sequence of edges that are added to the graph until some point. It is necessary to predict which edges will appear in the future in our graph. From the point of view of real life, this task is part of a recommender system - for example, forecasting connections (“friendships”) between two social users. network. In this problem, in fact, for each pair of arbitrarily selected vertices it is necessary to predict - what is the probability that there will be an edge between them in the future - here you just need to work with the characteristics and with the description of the vertices. For example, as one of the signs may be the intersection of sets of friends, or Jacquard measure. The reader is invited to think about possible metrics of similarity between vertices and write his own variation in the comments).
Allocation of communities in social networks
A task that is difficult to attribute to any specific tasks. Often, it is considered in the context of the task of "clustering on graphs." There are a lot of methods for solving this problem, from simple extraction of connected components (the algorithm was mentioned above) with a correctly defined subset of vertices, to sequential removal of edges from the graph until the desired component remains. Here, again - it is very important to first understand which communities we want to highlight on the network, i.e. first work with a description of the vertices and edges, and only then think about how to distinguish the communities themselves in the resulting subgraph.
Shortest graph distances
This task is also classical and is implemented, for example, in the same Yandex.Metro or other services that help find the shortest paths in a certain graph - whether it is a graph of connections between points of a city or a graph of acquaintances.
Or a task that a mobile operator, for example, can easily face:
Determining opinion leaders on the network
To promote, say, a new option, for example, the mobile Internet, in order to optimize the advertising budget, I would like to single out people who are in some ways surrounded by attention from . In our terms, these are the vertices of the graph that have great authority on the network - therefore, this task with the correct construction of the graph reduces to the PageRank problem.
So, we examined typical applied problems of graph analysis that may arise in practice, as well as one of the tools that can be used to solve them. This concludes the review of the Apache Spark library, and indeed the overview of tools, and in the future we will focus more on algorithms and specific tasks!
