Fundamentals of statistics: just about complex formulas
Statistics around us
Statistics and data analysis permeate almost any modern field of knowledge. It is becoming increasingly difficult to draw the line between modern biology, mathematics and computer science. Economic research and regression analysis are almost inseparable. One of the known methods for checking distribution for normality is the Kolmogorov-Smirnov criterion. Did you know that it was Kolmogorov who made a huge contribution to the development of mathematical linguistics?
While still a student of the Faculty of Psychology at St. Petersburg State University, I became interested in cognitive psychology. By the way, Immanuel Kant did not consider psychology to be a science, since he did not see the possibility of using mathematical methods in it. My current research is devoted to the modeling of mental processes, and I hope that such areas in modern cognitive psychology as computational and connectivist models would soften his attitude!
Of course, statistics are applied far beyond the boundaries of scientific laboratories: in advertising, marketing, business, medicine, education, etc. But, most interestingly, the basic knowledge of data analysis is extremely useful in everyday life. For example, I think you are all familiar with the concept of arithmetic mean. The average value is very often used in the media when discussing various socio-economic indicators - income, unemployment, etc. In 2005, the British media wrote that the average income level of the population not only did not increase, but decreased by 0.2% compared with the previous year. The headings “Population's incomes declined for the first time since 1990” flickered. Some politicians have even used this fact to criticize the current government. However, it’s important to understand that the arithmetic mean is a good indicator, when our trait has a symmetrical distribution (there are as many rich as poor). The actual distribution of income is rather as follows:
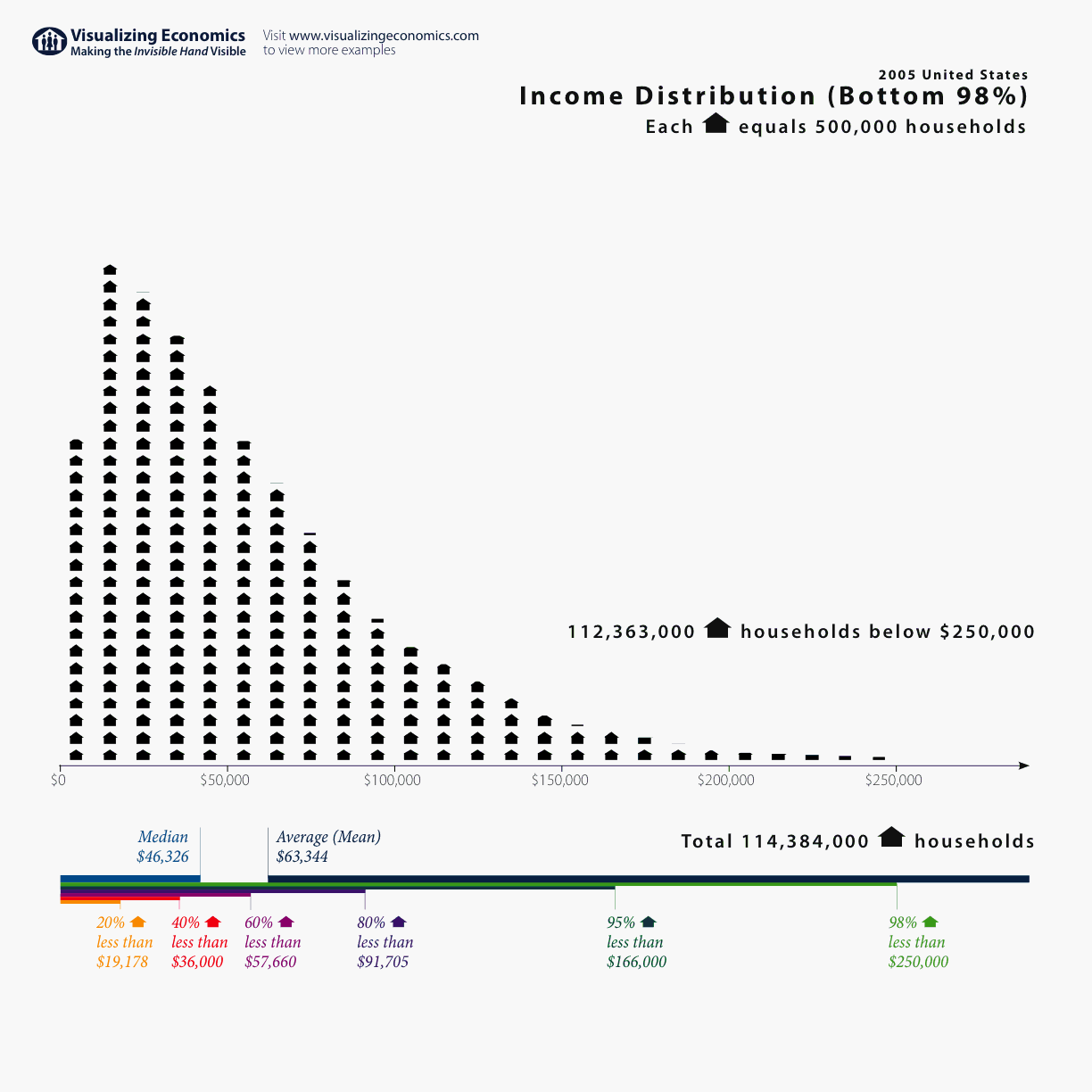
The distribution has a pronounced asymmetry: very wealthy people are noticeably less than the middle class. This leads to the fact that in this case, the bankruptcy of one of the millionaires can significantly affect this indicator. It is much more informative to use the median value to describe such data. Median is the salary value that is in the very middle of the income distribution (50% of all observations are less than the median, 50% more). And, surprisingly, the median income in 2005 in the UK, unlike the average, continued to grow. Thus, if you know about different types of distribution and different measures of the central tendency (average and median), then it is not so easy to mislead you in such cases as described in the example.
Statistic Analysis Black Box
As we have already found out, no matter what you plan to do, the probability of encountering the course “mathematical statistics in your area” is gradually approaching one. However, often classes on introducing statistics do not cause delight among students of non-technical faculties. After a few lessons, it turns out that such basic concepts as, for example, correlation are something like the following:
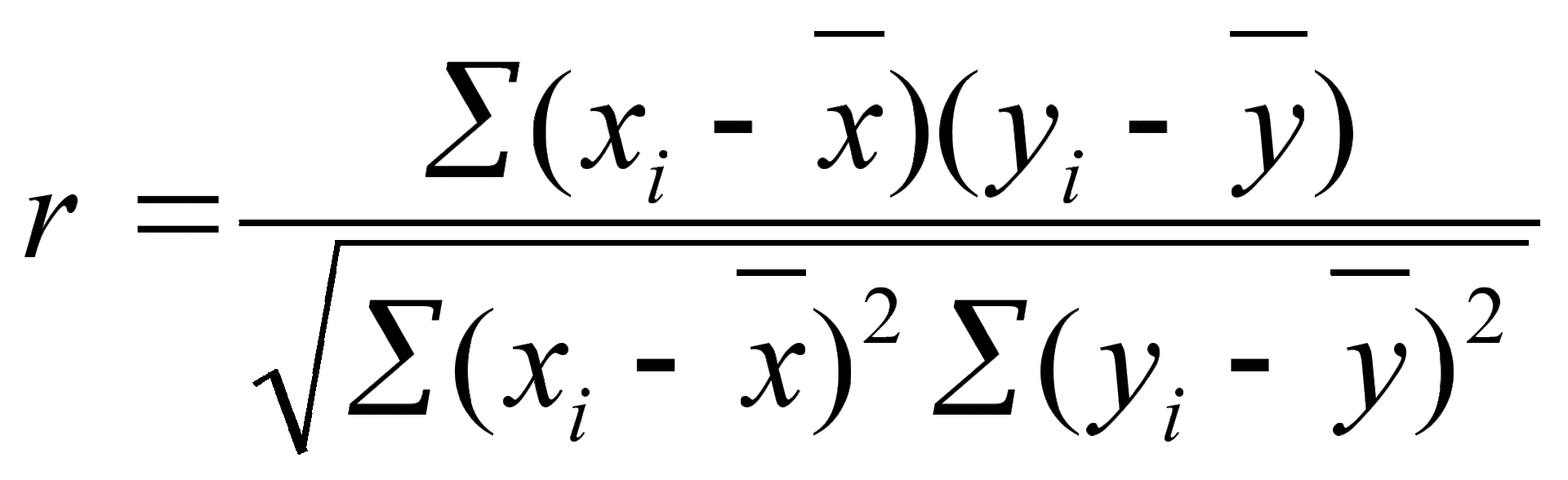
And, desperate to thoroughly understand the origin of these sums and square roots, a student can begin to perceive statistics as follows: “if r> 0, then a positive connection, and if less than 0, then a negative one”; “If p the significance level is less than 0.05, then it’s good, if from 0.05 to 0.1, it’s not very good, but if it is more than 0.1, it’s bad.” Helping students prepare for the exam, I have come across such spells more than once! Also, of course, no one calculates all these indicators manually, and using, for example, SPSS , you can google a second step-by-step instruction “how to compare two averages” in a second.
- Click here
- Remove / checkmark here
- p <0.05 -> profit
Statistical analysis begins to resemble a black box: data is input, output is a table of the main results and the value of the p-value (p-value), which will dot all the i.
What is p-value talking about?
Suppose we decide to find out if there is a relationship between addiction to bloody computer games and aggressiveness in real life. For this, two groups of schoolchildren were randomly formed, 100 people each (group 1 - fans of shooters, group 2 - not playing computer games). As an indicator of aggressiveness acts, for example, the number of fights with peers. In our imaginary study, it turned out that a group of school-gamers really really noticeably more often conflict with comrades. But how do we find out how statistically significant the differences are? Maybe we got the observed difference quite by accident? To answer these questions, the value of the p-level of significance (p-value) is used - this is the probability of getting such or more pronounced differences, provided that in the general population there are really no differences. In other words, it is likely to get such or even stronger differences between our groups, provided that, in fact, computer games do not affect aggressiveness. It doesn't sound so complicated. However, it is this statistical indicator that is very often interpreted incorrectly.
And now some examples about p-value

So, we compared the two groups of schoolchildren with each other in terms of aggressiveness using the standard t-test (or the non-parametric Chi criteria - the square more appropriate in this situation) and found that the coveted p-level of significance is less than 0.05 (for example, 0.04). But what does the resulting p-value of significance really tell us? So, if p-value is the probability of getting such or more pronounced differences, provided that in the general population there are really no differences, then what, in your opinion, is the correct statement:
- Computer games are the cause of aggressive behavior with a probability of 96%.
- The probability that aggressiveness and computer games are not related is 0.04.
- If we got a p-level of significance greater than 0.05, this would mean that aggressiveness and computer games are in no way connected.
- The probability of accidentally obtaining such differences is 0.04.
- All statements are incorrect.
If you chose the fifth option, then absolutely right! But, as numerous studies show, even people with significant experience in data analysis often incorrectly interpret the p-value (for example, you can see this interesting article ).
Let's look at all the answers in order:
- The first statement is an example of a correlation error: the fact of a significant relationship between two variables does not tell us anything about the causes and effects. Maybe it’s more aggressive people who prefer to spend time playing computer games, and not computer games make people more aggressive.
- This is a more interesting statement. The thing is that we initially accept for this, that in fact there are no differences. And, keeping this in mind as a fact, we calculate the p-value. Therefore, the correct interpretation: “If we assume that aggressiveness and computer games are not connected in any way, then the probability of getting such or even more pronounced differences was 0.04.”
- But what if we get insignificant differences? Does this mean that there is no connection between the studied variables? No, this only means that there may be differences, but our results did not allow them to be detected.
- This is directly related to the p-value definition itself. 0.04 is the probability of getting such or even more extreme differences. Estimating the probability of getting exactly such differences as in our experiment is, in principle, impossible!
These pitfalls can be hidden in the interpretation of such an indicator as p-value. Therefore, it is very important to understand the mechanisms underlying the methods of analysis and calculation of basic statistical indicators.
Statistics Essentials Online Course: Complex Formulas with Simple Language
Now I am writing a dissertation at the Faculty of Psychology of St. Petersburg State University and teaching statistics to biologists at the Institute of Bioinformatics. Based on the lecture course and my own research experience, the idea came up to create an online course on introducing statistics in Russian for everyone, not necessarily bioinformatics or biologists.
There are many good online courses on data analysis and statistics (e.g. such , such , or such), but almost all of them are in English. I hope that the course will be useful for those who are just getting acquainted with the basics of statistics. In it, I try to analyze the basic ideas and methods of data analysis in the most accessible form, paying particular attention to the very idea of statistical testing of hypotheses and interpretation of the results. Examples will include tasks from various fields: from bioinformatics to sociology. The course is free and all of its materials will remain open after graduation, starting February 15th.
Useful materials
If you know any useful courses or materials on the introduction to statistics - share in the comments!
