We decipher the Habra rating formula or the restoration of functional dependencies according to empirical data
If you ever read the help section on Habré, you probably saw a curious line there:
from which region it was equal to what?
Today we will answer this question.

(we measure Habra rating in parrots)
In this part, we will consider the basic properties that any rating function must satisfy, and using our knowledge of the subject area, we will try to guess the specific type of function.
What, in principle, depends on the rating? The rating of any user is formed using the actions of other users, or rather their voting for karma, topics and comments. Habra residents have no other ways to influence user indicators. This means that our function takes the input value of karma (rational), votes by topic (integer) and comments (integer) and returns a rational number.
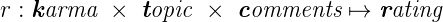
Moreover, we know that karma and votes for comments and topics independently influence the rating, which means that our ternary function breaks up into some composition of three unary ones. Suppose this is a sum of three functions.
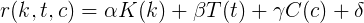
What boundary conditions should anyrating function? Boundary conditions - any new user has a rating of zero; if the user has not written a single post, it means that the contribution of posts to the rating is also equal to zero, etc.
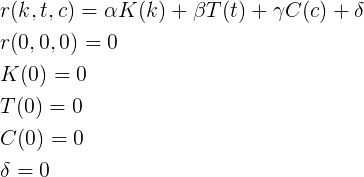
What else do we know about these features? They should be monotonically increasing and easy to calculate (that is, somehow simply expressed through elementary functions). Consider the simplest option - a linear relationship for each of the parameters.
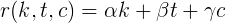
Using the boundary conditions, we can easily derive these coefficients. Consider the case when only karma has a contribution to the rating (i.e., there are no posts and comments for the last 30 days).

Substitute alpha equal to one tenth in the formula:

Having received the first coefficient, we can take another user for whom one of the undefined coefficients is zero and calculate the second coefficient:

Substitute 4/5 for the beta in the formula:
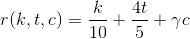
And the last stroke.
Taking any other user, and substituting all the parameters, we get that the gamma is 1/100.
Then, the rating function of karma k , votes for topics t and comments c is
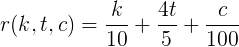
It is clear that the formula deduced from three points may be incorrect - there are an infinite number of functions passing through three points. Therefore, this hypothesis is worth checking. How? Let's try to get these coefficients directly from the data using classical regression and compare with the obtained ones.
If our hypothesis is true, then we will get a model with coefficients similar to analytical (and high parameters of confidence in the correctness of the model).
Data on the rating and the corresponding parameters of karma votes for posts and comments (there are many other interesting and delicious data Habra) are available here:
github.com/SergeyParamonov/HabraData/blob/master/users_rating.csv
proceed,
As we see, the value of the coefficients for karma and posts actually coincides, and judging by the parameters, the model is pretty confident in evaluating these two parameters. But what about the third parameter (contribution of comments to the rating)? And where did the difference in the coefficients come from, if it is known that the function should be deterministic?
It would seem that classical regression seriously contradicts the formula obtained by us - it differs in the estimation of the third parameter by 50% and does not ideally coincide in the other two. However, it is known that classical regression is incredibly unstable to statistical outliers. Let’s take a look at them, that is, at a set of points whose rating value differs significantly from the analytical formula we received.
Here you can see that the author of this article is on the list. Why? Because there is an article written 30 days ago, which means it did not fall into the data sample, but at the same time, the votes disappear within three days. Hence the difference in rating and testimony of the obtained formula.
But this is not true for all points, for example, take the Guderian entry . He has no boundary articles in the last 30 days. Where does the difference come from? Everything is very simple. TM incorrectly counted his rating on Habré, since his article moved to megamozg, and it’s precisely because of which he has the missing votes on the articles.

Bingo! We explained where the wrong points come from:
But all this sounds like a fit for the answer, and not a beautiful verification of a hypothesis, does it? And here comes to our aid ...
Suppose we have a set of outlier points in the sample and it is small, well, for example, up to 5%, and a sufficient sample of users (experimentally enough with 1,500 top), then we use the methods of regression resistant to emissions ( robust regression , and here's an interesting KDD topic tutorial ).
Let's try to use the method right out of the box:
Voila, the coefficients are found and they exactly coincide with those obtained analytically.
You can download it here and apply on this data.
For those who do not want to go far for a script:
Here, of course, an attentive reader can say: “Well, now TM will have to come up with a new secret rating calculation function”, and that’s why in this part we will discuss why it’s useless to hide the rating function.
Here are the main properties of the rating:
All this allows to restore this function automatically using elementary collected data , using methods of stable regression and selection of unary functions separately from each other. The introduction of noise, non-deterministic elements, and probabilities will only slightly complicate the task and possibly slightly affect the accuracy of the parameters.
Security through obscurity does not work here either.
When I wrote the Habr-monitor (this is part of Habr-analytics , if you write to Habr, then maybe the resource will be useful to you), which displays the change in the parameters of the article in time, the first thing I wanted to fasten was the change in votes in time. For a number of reasons, this option is not available for viewing before voting for a post. Having the analytical function for user rating, you can always display the rating of his current article (provided that it is one and he has no articles on which the votes are "lost" at the moment).
In fact, having this function, you can fasten the article rating parameter to the monitor (picture below) .
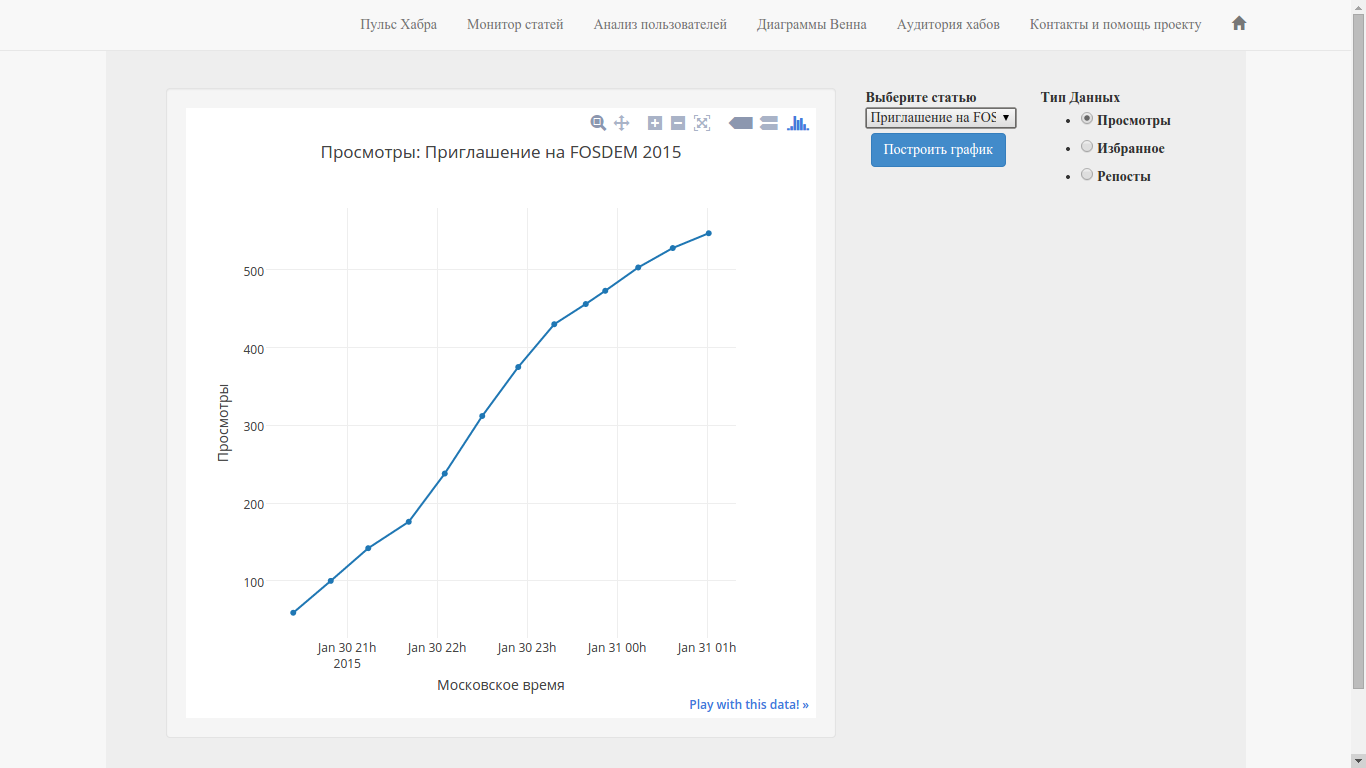
This will also allow SoHabr to fasten the rating of articles.
Votes for comments have practically no contribution to the rating, even the most rated comments in the entire history of Habr (~ 400 +) add 4-5 points to the rating, that is, as much as the article with 6-7 pluses.
Karma has lost its weight in relation to the rating, previously it had a coefficient of 0.5, and now 0.1, which makes the top much more dynamic (previously it was almost impossible to enter the top 10).
Every 5 votes for an article brings 4 points to the rating, that is, multiplying by 0.8 votes of the article, we get an increase in the rating. At the moment, this is the most significant and in fact the only factor determining the user's rating.
And yet, X = 80 .
PS statement ( from here )
Suppose you wrote a publication with a rating of +100 - this added an X value to your personal rating. After a few dozen days, that same X will be subtracted, thereby returning you to your previous place.then they probably wondered what kind of X it was and
Today we will answer this question.

(we measure Habra rating in parrots)
Article structure
- Analytical conclusion
- Regression
- Exceptions
- Sustainable Regression
- Script and data
- Why hiding a function is useless
- What can be done with this?
- Interpretation of the formula
Analytical conclusion
In this part, we will consider the basic properties that any rating function must satisfy, and using our knowledge of the subject area, we will try to guess the specific type of function.
Key Assumptions
What, in principle, depends on the rating? The rating of any user is formed using the actions of other users, or rather their voting for karma, topics and comments. Habra residents have no other ways to influence user indicators. This means that our function takes the input value of karma (rational), votes by topic (integer) and comments (integer) and returns a rational number.
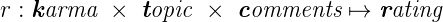
Moreover, we know that karma and votes for comments and topics independently influence the rating, which means that our ternary function breaks up into some composition of three unary ones. Suppose this is a sum of three functions.
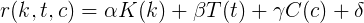
What boundary conditions should anyrating function? Boundary conditions - any new user has a rating of zero; if the user has not written a single post, it means that the contribution of posts to the rating is also equal to zero, etc.
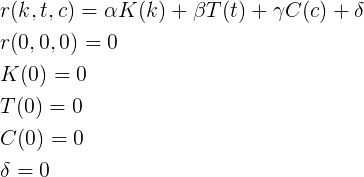
What else do we know about these features? They should be monotonically increasing and easy to calculate (that is, somehow simply expressed through elementary functions). Consider the simplest option - a linear relationship for each of the parameters.
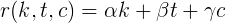
Odds output
Using the boundary conditions, we can easily derive these coefficients. Consider the case when only karma has a contribution to the rating (i.e., there are no posts and comments for the last 30 days).

Substitute alpha equal to one tenth in the formula:

Having received the first coefficient, we can take another user for whom one of the undefined coefficients is zero and calculate the second coefficient:

Substitute 4/5 for the beta in the formula:
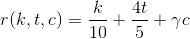
And the last stroke.
Final formula
Taking any other user, and substituting all the parameters, we get that the gamma is 1/100.
Then, the rating function of karma k , votes for topics t and comments c is
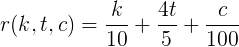
Regression
It is clear that the formula deduced from three points may be incorrect - there are an infinite number of functions passing through three points. Therefore, this hypothesis is worth checking. How? Let's try to get these coefficients directly from the data using classical regression and compare with the obtained ones.
If our hypothesis is true, then we will get a model with coefficients similar to analytical (and high parameters of confidence in the correctness of the model).
Data on the rating and the corresponding parameters of karma votes for posts and comments (there are many other interesting and delicious data Habra) are available here:
github.com/SergeyParamonov/HabraData/blob/master/users_rating.csv
proceed,
1478 users regular regression
Call:
lm(formula = rating ~ karma + topic_score + comment_score - 1, data = data)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
karma 0.1017172 0.0006097 166.842 < 2e-16 ***
topic_score 0.7862749 0.0020999 374.428 < 2e-16 ***
comment_score 0.0153159 0.0031884 4.804 1.72e-06 ***
As we see, the value of the coefficients for karma and posts actually coincides, and judging by the parameters, the model is pretty confident in evaluating these two parameters. But what about the third parameter (contribution of comments to the rating)? And where did the difference in the coefficients come from, if it is known that the function should be deterministic?
Exceptions
It would seem that classical regression seriously contradicts the formula obtained by us - it differs in the estimation of the third parameter by 50% and does not ideally coincide in the other two. However, it is known that classical regression is incredibly unstable to statistical outliers. Let’s take a look at them, that is, at a set of points whose rating value differs significantly from the analytical formula we received.
>data$dif <- abs(rating - karma/10 - topic_score*0.8 - comment_score/100)
>print(data[data$dif > 2, ])
user rating karma topic_score comment_score dif
akrot 80.21 25.00 91 13 4.780
anegrey 60.30 31.50 114 15 34.200
Guderian 56.02 119.00 32 6 18.460
ilusha_sergeevich 154.27 157.75 177 11 3.215
ParyshevD 69.27 42.00 130 7 39.000
PatapSmile 48.75 246.00 0 0 24.150
rw6hrm 38.81 33.00 71 1 21.300
varagian 81.34 170.00 50 34 24.000
Here you can see that the author of this article is on the list. Why? Because there is an article written 30 days ago, which means it did not fall into the data sample, but at the same time, the votes disappear within three days. Hence the difference in rating and testimony of the obtained formula.
But this is not true for all points, for example, take the Guderian entry . He has no boundary articles in the last 30 days. Where does the difference come from? Everything is very simple. TM incorrectly counted his rating on Habré, since his article moved to megamozg, and it’s precisely because of which he has the missing votes on the articles.

Bingo! We explained where the wrong points come from:
- boundary articles written 30 to 33 days ago with fading voices;
- moving and dividing Habr;
- articles removed in draft or offtopic (by UFO or author).
But all this sounds like a fit for the answer, and not a beautiful verification of a hypothesis, does it? And here comes to our aid ...
Sustainable Regression
Suppose we have a set of outlier points in the sample and it is small, well, for example, up to 5%, and a sufficient sample of users (experimentally enough with 1,500 top), then we use the methods of regression resistant to emissions ( robust regression , and here's an interesting KDD topic tutorial ).
Let's try to use the method right out of the box:
library("MASS")
...
Call: rlm(formula = rating ~ karma + topic_score + comment_score - 1, data = data)
Coefficients:
Value Std. Error t value
karma 0.10 0.00 23463021.30
topic_score 0.80 0.00 54494665.88
comment_score 0.01 0.00 448681.05
Voila, the coefficients are found and they exactly coincide with those obtained analytically.
Script and data
You can download it here and apply on this data.
For those who do not want to go far for a script:
R regression code
library("MASS")
data <- read.csv("users.csv", header=T, stringsAsFactors=F)
names(data) <- c("user","rating","karma","topic_score","comment_score")
fit <- lm(data=data, rating ~ karma + topic_score + comment_score - 1)
print("regular regression")
print(summary(fit))
fit <- rlm(data=data, rating ~ karma + topic_score + comment_score - 1)
print("robust regression")
print(summary(fit))
attach(data)
data$dif <- abs(rating - karma/10 - topic_score*0.8 - comment_score/100)
print(data[data$dif > 2, ])
Why hiding a function is useless
Here, of course, an attentive reader can say: “Well, now TM will have to come up with a new secret rating calculation function”, and that’s why in this part we will discuss why it’s useless to hide the rating function.
Here are the main properties of the rating:
- the rating depends only on the actions of other users and voting channels, of which there are only three: votes for posts, comments and karma;
- votes for posts, karma and comments are independent of each other i.e. the function is always decomposed into some composition of three independent unary functions from posts, comments and karma;
- each of these functions should be easy and quick to calculate, since rating indicators need to be constantly recounted for a large number of users;
- for the same reason, it should be expressible in elementary and monotonically increasing functions;
- the function should be deterministic and noise-free, i.e., for two users with equal karma, votes for posts and comments, the rating should be the same (for an effective period = 30 days).
All this allows to restore this function automatically using elementary collected data , using methods of stable regression and selection of unary functions separately from each other. The introduction of noise, non-deterministic elements, and probabilities will only slightly complicate the task and possibly slightly affect the accuracy of the parameters.
Security through obscurity does not work here either.
What can be done with this?
When I wrote the Habr-monitor (this is part of Habr-analytics , if you write to Habr, then maybe the resource will be useful to you), which displays the change in the parameters of the article in time, the first thing I wanted to fasten was the change in votes in time. For a number of reasons, this option is not available for viewing before voting for a post. Having the analytical function for user rating, you can always display the rating of his current article (provided that it is one and he has no articles on which the votes are "lost" at the moment).
In fact, having this function, you can fasten the article rating parameter to the monitor (picture below) .

This will also allow SoHabr to fasten the rating of articles.
Interpretation of the formula
Votes for comments have practically no contribution to the rating, even the most rated comments in the entire history of Habr (~ 400 +) add 4-5 points to the rating, that is, as much as the article with 6-7 pluses.
Karma has lost its weight in relation to the rating, previously it had a coefficient of 0.5, and now 0.1, which makes the top much more dynamic (previously it was almost impossible to enter the top 10).
Every 5 votes for an article brings 4 points to the rating, that is, multiplying by 0.8 votes of the article, we get an increase in the rating. At the moment, this is the most significant and in fact the only factor determining the user's rating.
And yet, X = 80 .
PS statement ( from here )
[...] over time, the rating will take on the value of half karma.already wrong.
