Twenty puzzles (on crazy, amazing geometry)
- Transfer
Warning doctor. Beware of these puzzles. Side effects can include lost afternoons, crumpled hair, and exclamations “Ahhhhhhhhhhhhh, how it is done” so loud that they can crack window glass.
A few months ago, I stumbled on Twitter on Ekaterin's Shearer's mathematical puzzle . They immediately fascinated me: each puzzle is so tangible, handmade, as if asking for it to be solved. And for each you can easily spend an hour of time, or even more.
Ekaterin allowed me to hang you on these puzzles - and shared 20 of her favorite puzzles. She even satisfied my curiosity and admiration by giving an interview (see the end of the article).
Enjoy. And do not say that the doctor did not warn.
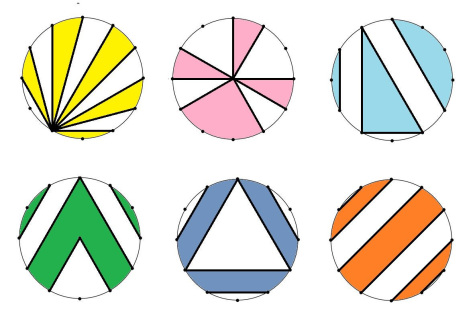
What part of each circle is painted over? (12 points at equal distance; the only point inside the circle is its center)
“Unfortunately, of these six, my favorite is the only one that I didn’t think of myself,” says Ekaterin, “it is dark blue.”
(As for me, this is a classic).
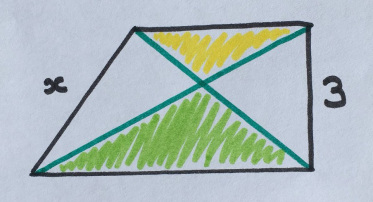
In a rectangular trapezium, the green area is 6 more than the yellow one. What is x?
"This is the" second version "of this puzzle: it is better than the first one I thought up."

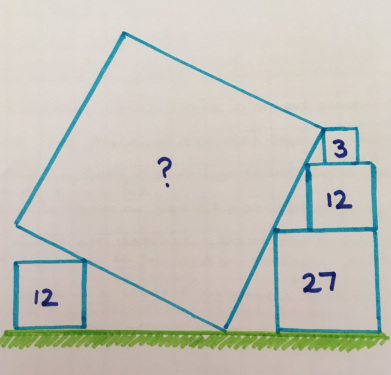
The lengths of the sides of three squares are consecutive integers. What is the total area?
“I like this one very much: on the basis of it I drew a lot of beautiful patterns.”
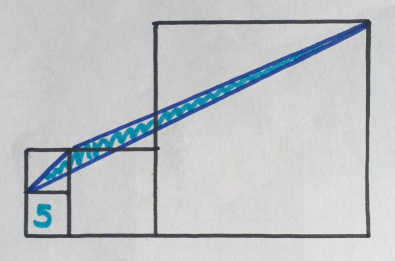
The area of the lower left square 5. What is the area of the blue triangle?
“Probably my favorite for all time. Looks just impossible! Here the solution method is called “haircut”, shearing (unfortunately, not in my honor). ”

"Another alteration, which I prefer the original."
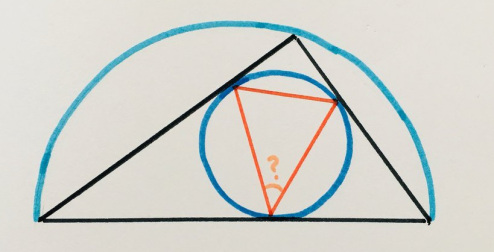
“Puzzles with corners are much harder to make. The students said that it was a rather simple task, but my parents had great difficulties. It seems that this puzzle requires more "knowledge," but the solution process itself is simpler. "

What is the area of the circle?
“In school, I did not study the theorem on intersecting chords, so I like to use it everywhere!”
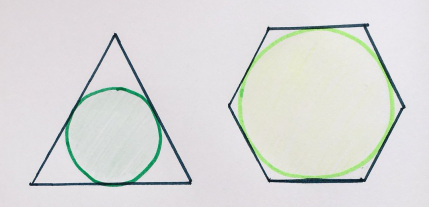
These regular polygons have the same perimeter. Find the ratio of the areas of the inscribed circles.
“This is a consequence of another puzzle, but I like it more than the original!”
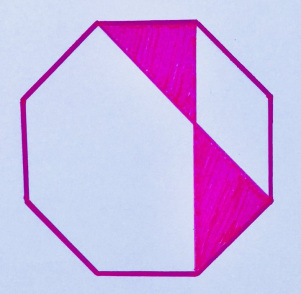
The shaded area has the same value as the perimeter of a regular octagon. What is the meaning?
“I think this is a pretty pure task, although it looks like a massive looting of Ed Southall's puzzles.”

"I like the fact that although you can find all sides of the orange triangle here (and I did it when I decided), but in fact it is not necessary - there is enough area and hypotenuse."
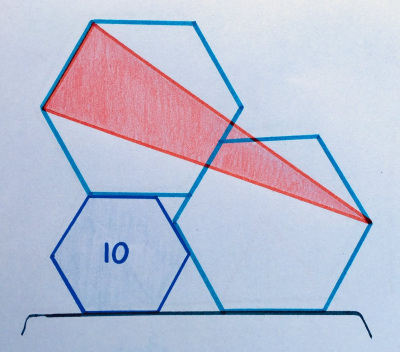
Two of the regular hexagons are identical; The third area is 10. What is the area of the red triangle?
“Not bad enough: I like that you don’t have to deal with any length of side, which are almost certainly terrible.”
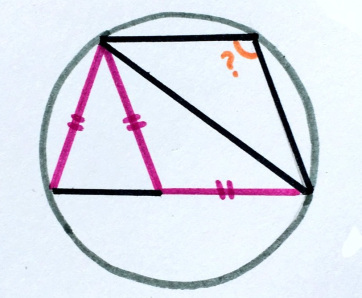
All four triangles are isosceles. Find the angle.
“I think that the formulation of this problem is perfect. Many miss important information and come to the conclusion that there are an infinite number of solutions! ”

Is the picture more green or blue (and how much)?
"Another one of my favorites."
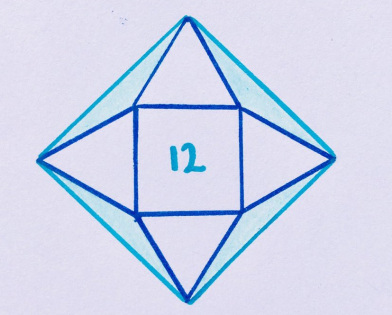
Four equilateral triangles are located around a square with an area of 12. What is the shaded area?
"The best here is really good solutions for dissecting the area."
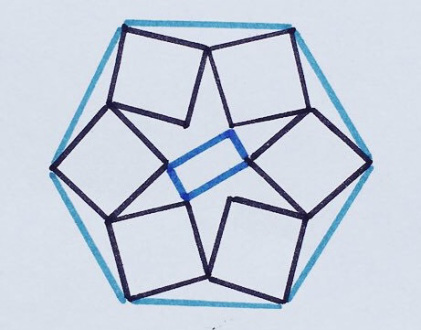
Six identical squares and a smaller rectangle are inscribed in this regular hexagon. What part of the hexagon do they occupy?
“The answer here is not so beautiful, but I was very surprised. I think, because of its complexity, this task has not received such a spread on Twitter, like others! ”
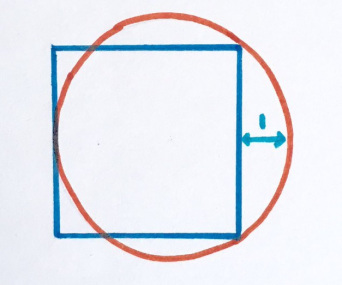
What is the area of this square?
"This is one of my favorites, because at first it seems that information is not enough."

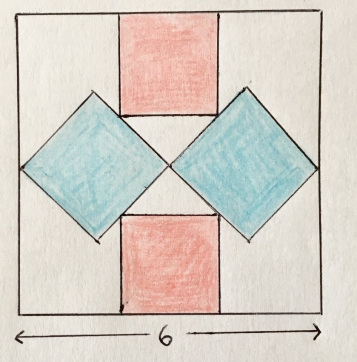
What part of a large square is painted over?
“Here I like the confusion of squares, as they rumble around as if in a washing machine. And the answer is also amazingly beautiful. ”
The squares of the same color are the same size. What is the area of all shaded areas?
“It's quite simple once you understand - but I didn't understand right away, so the simplicity of the answer surprised me.”

What part of the shape is painted over? The hexagon is regular, with evenly spaced points along the perimeter.
“I rarely published this. But the picture reminds me of Tigra Tony [with packs of Kellogg quick breakfast - approx. trans.]
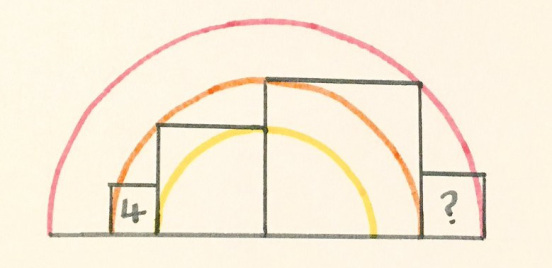
The left square has an area of 4. What is the area of the right square?
“I like this task, it reminds of the sunset over the city of squares.”
If you have read this far — perhaps 6 months after the start of reading — and your table is surrounded by crumpled papers and empty Chinese food containers, then you will be pleased to read a short interview with Ekaterin.
How did you come to develop your puzzles?
I went on vacation to the Scottish highlands, but forgot to take a coat, so I had to sit in the house alone, while my friends were walking in nature! Nothing remained but to mechanically draw lines on a piece of paper.
I didn’t expect it to turn into a hobby, but it is a bit addictive, especially when people send back their decisions that I like. Almost always you can beautifully reduce the puzzle that I missed.
How is the creative process?
It all starts with drawing meaningless figures. The result is a whole page of overlapping squares at different angles or regular (type) pentagons with different colored parts, and then I see if there is any good mathematics there — the relationship between lengths or areas or angles.
Many of your tasks are drawn with a marker on paper. Why such lowtek?
I tried to use Desmos and Geogebra, but I didn’t like it very much. In my opinion, it is faster to draw the inscribed circle manually, after a small amount of trial and error, than to beautifully build it in software geometry.
In addition, when using the pen, you can invent things, because the lines are so thick. This is a good compromise between looking “right,” but also knowing that you can't just pull out a ruler and measure a shape.
One of the nice things about geometry is that it forgives a lot. I can show you a hopeless square or circle, but this is enough to convey the concept because they are so well defined.
Some of your puzzles give the least information. How do you find this boundary, where the diagram is just defined?
Sometimes this minimum is actually a hint, because it sends you along the same road. I prefer to give a little more than necessary, so there are several deceptive routes. It also gives a greater variety of solutions!
It was the case, I published a couple of impossible puzzles: fortunately, someone usually points this out pretty quickly!
I also published puzzles with a massive amount of unnecessary information, because I did not see a good solution in order to use only half of the information.
Tips for potential puzzle makers?
Well, here my impostor syndrome will fully manifest. I'm definitely still new - I have been doing this only since August [article published in October 2018 - approx. lane]! On the other hand, I like to create puzzles and read solutions even more than solve them myself.
The main goal of the puzzle should be entertainment - this is what distinguishes it from a standard mathematical task. Thus, you need at least two of the three:
In principle, start drawing - find the puzzle that you like to solve, and think about how you can expand or change some of the elements. If you suddenly find relationships that surprise you, then with a high probability they will surprise others. Twitter is a great platform, as people can post their own pictures in response.
A few months ago, I stumbled on Twitter on Ekaterin's Shearer's mathematical puzzle . They immediately fascinated me: each puzzle is so tangible, handmade, as if asking for it to be solved. And for each you can easily spend an hour of time, or even more.
Ekaterin allowed me to hang you on these puzzles - and shared 20 of her favorite puzzles. She even satisfied my curiosity and admiration by giving an interview (see the end of the article).
Enjoy. And do not say that the doctor did not warn.
1. Garden hours

What part of each circle is painted over? (12 points at equal distance; the only point inside the circle is its center)
“Unfortunately, of these six, my favorite is the only one that I didn’t think of myself,” says Ekaterin, “it is dark blue.”
2. Tilted square

(As for me, this is a classic).
3. It's a trap.

In a rectangular trapezium, the green area is 6 more than the yellow one. What is x?
"This is the" second version "of this puzzle: it is better than the first one I thought up."
4. Three square plates

The lengths of the sides of three squares are consecutive integers. What is the total area?
“I like this one very much: on the basis of it I drew a lot of beautiful patterns.”
5. Beautiful haircut

The area of the lower left square 5. What is the area of the blue triangle?
“Probably my favorite for all time. Looks just impossible! Here the solution method is called “haircut”, shearing (unfortunately, not in my honor). ”
6. All people are born equal.

"Another alteration, which I prefer the original."
7. Semicircle Turdaken

“Puzzles with corners are much harder to make. The students said that it was a rather simple task, but my parents had great difficulties. It seems that this puzzle requires more "knowledge," but the solution process itself is simpler. "
8. Power chords

What is the area of the circle?
“In school, I did not study the theorem on intersecting chords, so I like to use it everywhere!”
9. The Tale of Two Circles
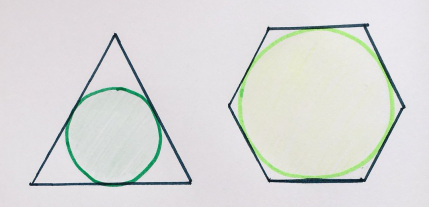
These regular polygons have the same perimeter. Find the ratio of the areas of the inscribed circles.
“This is a consequence of another puzzle, but I like it more than the original!”
10. Doc Oct

The shaded area has the same value as the perimeter of a regular octagon. What is the meaning?
“I think this is a pretty pure task, although it looks like a massive looting of Ed Southall's puzzles.”
11. Everything in the square

"I like the fact that although you can find all sides of the orange triangle here (and I did it when I decided), but in fact it is not necessary - there is enough area and hypotenuse."
12. Spike in the hive

Two of the regular hexagons are identical; The third area is 10. What is the area of the red triangle?
“Not bad enough: I like that you don’t have to deal with any length of side, which are almost certainly terrible.”
13. I have seen isosceles.

All four triangles are isosceles. Find the angle.
“I think that the formulation of this problem is perfect. Many miss important information and come to the conclusion that there are an infinite number of solutions! ”
14. Green against blue

Is the picture more green or blue (and how much)?
"Another one of my favorites."
15. Stone cutters

Four equilateral triangles are located around a square with an area of 12. What is the shaded area?
"The best here is really good solutions for dissecting the area."
16. Going, going, corner

Six identical squares and a smaller rectangle are inscribed in this regular hexagon. What part of the hexagon do they occupy?
“The answer here is not so beautiful, but I was very surprised. I think, because of its complexity, this task has not received such a spread on Twitter, like others! ”
17. Only one fact

What is the area of this square?
"This is one of my favorites, because at first it seems that information is not enough."
18. Washing machine

What part of a large square is painted over?
“Here I like the confusion of squares, as they rumble around as if in a washing machine. And the answer is also amazingly beautiful. ”
19. Flying flags

The squares of the same color are the same size. What is the area of all shaded areas?
“It's quite simple once you understand - but I didn't understand right away, so the simplicity of the answer surprised me.”
20. Tigrogon

What part of the shape is painted over? The hexagon is regular, with evenly spaced points along the perimeter.
“I rarely published this. But the picture reminds me of Tigra Tony [with packs of Kellogg quick breakfast - approx. trans.]
BONUS:
Sunset over the Square City
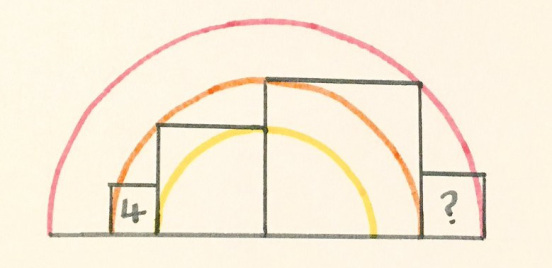
The left square has an area of 4. What is the area of the right square?
“I like this task, it reminds of the sunset over the city of squares.”
If you have read this far — perhaps 6 months after the start of reading — and your table is surrounded by crumpled papers and empty Chinese food containers, then you will be pleased to read a short interview with Ekaterin.
How did you come to develop your puzzles?
I went on vacation to the Scottish highlands, but forgot to take a coat, so I had to sit in the house alone, while my friends were walking in nature! Nothing remained but to mechanically draw lines on a piece of paper.
I didn’t expect it to turn into a hobby, but it is a bit addictive, especially when people send back their decisions that I like. Almost always you can beautifully reduce the puzzle that I missed.
How is the creative process?
It all starts with drawing meaningless figures. The result is a whole page of overlapping squares at different angles or regular (type) pentagons with different colored parts, and then I see if there is any good mathematics there — the relationship between lengths or areas or angles.
Many of your tasks are drawn with a marker on paper. Why such lowtek?
I tried to use Desmos and Geogebra, but I didn’t like it very much. In my opinion, it is faster to draw the inscribed circle manually, after a small amount of trial and error, than to beautifully build it in software geometry.
In addition, when using the pen, you can invent things, because the lines are so thick. This is a good compromise between looking “right,” but also knowing that you can't just pull out a ruler and measure a shape.
One of the nice things about geometry is that it forgives a lot. I can show you a hopeless square or circle, but this is enough to convey the concept because they are so well defined.
Some of your puzzles give the least information. How do you find this boundary, where the diagram is just defined?
Sometimes this minimum is actually a hint, because it sends you along the same road. I prefer to give a little more than necessary, so there are several deceptive routes. It also gives a greater variety of solutions!
It was the case, I published a couple of impossible puzzles: fortunately, someone usually points this out pretty quickly!
I also published puzzles with a massive amount of unnecessary information, because I did not see a good solution in order to use only half of the information.
Tips for potential puzzle makers?
Well, here my impostor syndrome will fully manifest. I'm definitely still new - I have been doing this only since August [article published in October 2018 - approx. lane]! On the other hand, I like to create puzzles and read solutions even more than solve them myself.
The main goal of the puzzle should be entertainment - this is what distinguishes it from a standard mathematical task. Thus, you need at least two of the three:
- Beautiful task setting . Provide a minimum of information so that the reader wonders how this problem can be solved at all. Or a few tantalizing pieces of information, each of which supposedly offers a solution. Regular polygons and circles are fantastic because they hide a huge amount of information.
- Beautiful method . The trick is either the shortest way or a sudden insight that simplifies everything. This may not be the most obvious method. I saw a lot of problems that are solved with the help of algebra or irrational numbers, or terrible expressions with pi, and at the end everything suddenly shrinks - and I understand that there is a simpler way.
- Beautiful answer . It’s not a pleasure to work on a puzzle in order to get an ugly answer at the end.
In principle, start drawing - find the puzzle that you like to solve, and think about how you can expand or change some of the elements. If you suddenly find relationships that surprise you, then with a high probability they will surprise others. Twitter is a great platform, as people can post their own pictures in response.
