Sort on a singly linked list in O (nlogn) time in the worst case with O (1) extra memory
It all started with this topic on the gamedev.ru website. Topikstarter suggested finding a sort that has the following properties:
Reservations for all three restrictions:
All the information that we know about the elements of the array is that they all form a linearly ordered set . All we can do is compare two elements of the array (for O (1)) and swap them (also for O (1)).
Under the cut you can find out what happened with us.
Challenge Before you look under the cat, I suggest that you first think about the algorithm yourself. If you come up with something cooler than our option - write in the comments.
I will make a reservation that there was no thorough search on the articles - perhaps we re-opened some already known algorithm, or the algorithm that solves this problem has long been known (perhaps much more efficient than ours).
The practical application of our algorithm is hardly possible, the task is more of academic interest.
Known sorts that immediately come to mind do not satisfy all three points at the same time, for example:
In the first comment, a friend of FordPerfect proposed the Median of Medians algorithm, which was not very well known in wide circles. Other BFPRT its name from the names of scientists who invented it: Manuel B lum, Robert W. F Lloyd Vaughn R Ratt, Ronald L. P ivest and Robert E. T Arjan. The algorithm is described on Wikipedia ( ru , en ), as well as in Kormen, but I will tell you a little about it, because on Wikipedia it is described so clumsy that I understood its essence only after comparing the Russian and English versions (and I also had to look into the original article) And on Habré his description was not yet. In Cormen, if anything, the description is normal, but I learned later that this algorithm is there. If you already know this algorithm, you can skip this piece of the article.
The Median of Medians algorithm allows you to find the kth ordinal statistics on any array in linear time in the worst case. The C ++ STL library has a similar algorithm, std :: nth_element, which also finds the kth ordinal statistics for linear time, but on average, because it is based on the Quickselect algorithm. The latter is essentially a quick sort, in which at each step we go down only one branch of recursion (more about Quickselect can be read here and here) Median of Medians is a modification of the Quickselect algorithm and does not allow the selection of a bad element for "branching", which in the worst case leads to a squared time.
Why do we need this Median of Medians? Yes, everything is quite simple - with its help, you can find the median of the array (n / 2nd order statistics) in linear time and branch the fast sorting algorithm on this element. This will cause quick sort to work for O (nlogn) not on average, but in the worst case.
Description of the Median of Medians algorithm. Input data: an array (specified, for example, by the first and last elements of the list) and the number k - which account element do we need to find.
Consider what is happening here as an example. Let there be an array and we want to find its median:

There are 27 different numbers from 1 to 27. We are looking for the 14th element in a row. We divide the elements into blocks of length 5 and sort the numbers inside each block: The

medians of each block are highlighted in yellow. We move them to the beginning of the array and recursively run our algorithm to search for the median in it:

I will not paint what happens inside the recursion, one thing is clear - the desired median will be 12.

This number 12 - the supporting element or median of the medians - has the following remarkable property. Let's go back a couple of pictures and mentally move our blocks as follows:
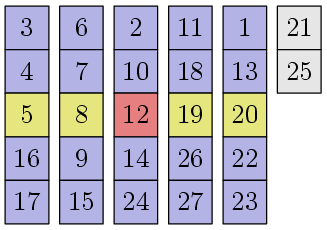
All columns are sorted by the middle element, plus the elements in each column are also sorted. We can see that approximately 30% of the elements (3 / 10n + O (1), to be precise), which are higher and to the left of the support element, are not larger than it. Similarly, for about 30% of the elements below and to the right of the support element - they are no less than it. This means that when we carry out the separation procedure, approximately 30% of all elements will necessarily be to the left of the support element and approximately 30% to the right:

In fact, there is a slight inaccuracy: we are lucky with the fact that there are exactly one piece of elements equal to the reference one. If there are a lot of such elements, then they all form a whole block and it is not clear where exactly the supporting element will fit. But it doesn’t really matter. We know that elements that are not less than the supporting element are at least 30%, which means elements that are strictly smaller than the supporting element are not more than 70%. Similarly - elements that are strictly larger than the supporting element are also no more than 70%. Thus, the sizes of the first and third blocks from the description of the algorithm above will always have a length of not more than 7 / 10n + O (1)!

We continue the analysis of the example. After the separation procedure, it becomes clear that our 14th element is in the third block, so we recursively run the entire algorithm for it, but now we are looking for the 2nd element in it.
What is the complexity of our algorithm?
Let T (n) be the worst case number operation of the Median of Medians algorithm for an array of length n. At each step, the algorithm invokes itself twice twice. The first time is to find the median of the medians on an array of n / 5 + O (1) elements in length. The second time - reducing the search space, while in the worst case, the size of the array decreases to 7 / 10n + O (1). All other operations require linear time.
As a result, we obtain the relation: T (n) = T (2 / 10n) + T (7 / 10n) + Cn, where C is a constant.
We expand this relation:
T (n) = Cn + (2/10 + 7/10) Cn + (2/10 + 7/10) (2/10 + 7/10) Cn + ... = Cn * ∑ i = 0 ..∞ (9/10) i = 10Cn = O (n)
Great! The algorithm has linear complexity!
Median of Medians is easy to implement on lists using recursion, which gives us a good partial solution to the original problem: guaranteed sorting for O (nlogn) on a singly linked list using O (logn) memory.
Code .
Let's get rid of recursion now.
To get started, let's remove the recursion from the actual quick sort. How to do this is not entirely obvious, so in this section we will look at how to do it.
This section will describe the idea that Comrade FordPerfect suggested on the gamedev.ru forum (yes, in fact, all the ideas in this article are not mine - I just posted it). The source of the idea is unknown, Google for the most part is silent and gives a lot of links to the so-called iterative quicksort, where the stack is emulated quite often (however, there was a discussion of a similar idea), and FordPerfect says that it was invented by his classmate for 40 minutes to think about the “quicksort with O (1) memory” task. The name “Flat quick sort” is also self-made, perhaps this algorithm is known under a different name.
Let's remember how regular recursive quicksort works. Input data: an array specified, for example, by two iterators on the start and end elements of a simply connected list.
The information that we need to remember during the recursion is where the third block begins and ends.
We note the following thing: any element of the first block is smaller than any element of the second block, and any element of the second block is smaller than any element of the third block.
The idea is this: let's move the largest element to the beginning of the block in each block. Then we can unambiguously determine where the next block will begin! To do this, we will just go from the beginning of the block until we meet an element strictly larger - it will signal the beginning of the next block!
Now the quick sort algorithm can be rewritten as follows:
Now let's look at this algorithm using an example:

Somewhere I already saw this array ... Let's arrange the pointers X, Y and Z:

The XZ block is not sorted. Then we find the median:

We assume that the median search procedure mixes the elements in the most bizarre way, leaving the median itself at the very beginning (for illustration purposes, an implementation may, for example, return an iterator to an element that is a median). Ok, let's now perform the separation procedure:

3 blocks are obtained. Block the last block and move Z to the end of the first block:

Now we start from the beginning. The current XZ block is not sorted, so we are looking for the median in it

:

Perform the separation procedure: Block the third block and move Z to the end of the first block:

Again look at XZ:

We are lucky! The block is sorted, so you can leave it alone and look for the next block. The X and Z pointers will move as follows:

Suddenly, this block is also sorted, since this is the second block of the previous step. We are looking for the following block: We
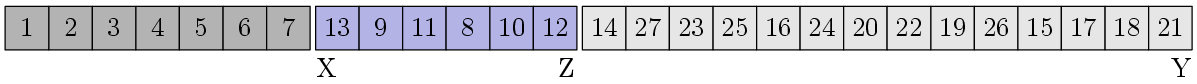
check for ordering - alas, this time we were not lucky, we have to arrange it. We find the median, and then do the separation procedure:

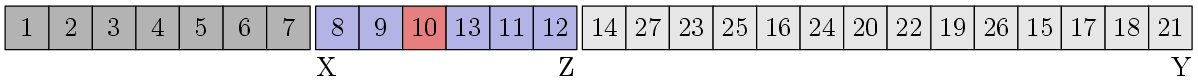
Next, we go to block [8,9], it is sorted, so X and Z will move to block [10], which is also sorted, after which the algorithm will consider the block [13, 11, 12], in which everything is already completely trivial. Sorting analysis of the second half of the array is proposed to be performed by the reader independently.
Code .
Unfortunately, with Median of Medians, such a trick as using the maximum element to identify blocks in flat quick sort will not work, because the elements of the array each time are mixed in unclear how. Here we will use a different focus.
In fact, to make quick sort work for guaranteed O (nlogn), it is not necessary to find the exact median for the split stage. It is enough to find something approximate. If we guarantee that the first and third blocks after the separation stage will not exceed Cn for some specific C <1, quick sort will work for O (nlogn). Even for C = 0.99. With afierce frenzied hidden constant, but O (nlogn)!
Therefore, we modify the Median of Medians so that it finds the median with some error K = O (log 2n). That is, an element will be found whose serial number is somewhere in the range from n / 2-K / 2 to n / 2 + K / 2. Since K is of the order of the degree of the logarithm, it is easy to find such a (concrete) n starting from which the segment [n / 2-K / 2, n / 2 + K / 2] lies, say, between 1 / 4n and 3 / 4n. For all smaller n, you can sort by just a bubble.
Why is K = O (log 2 n)? Yes, we just use K array elements in order to store in them all the necessary information on the stack (the idea, again, is FordPerfect comrade). The recursion levels are O (logn), on each of them we need to store O (1) numbers per O (logn) bit. And find the median for quick sort among the remaining NK elements.
Each bit is represented by two consecutive different elements of the array. If the first of them is less than the second, the bit stores the state 0, otherwise - 1 (or vice versa). The first task that we need to solve is to find K / 2 pairs of different elements of the array and understand what to do if so many pairs are not found.
This is done very simply. Let the iterators X and Y point to the first element of the array. We will move Y forward until we find an element that is not equal to X. If you find it, move X forward, swap the elements that X and Y point to, move X forward again (+ you still need to handle the small case - move Y forward if faced X). And so until we find K / 2 pairs. What if Y has already reached the end of the array and K / 2 pairs have not yet been found? This means that all elements from X to Y inclusive are the same! (It is quite simple to verify that this invariant is preserved throughout the execution of the entire algorithm). Then, as a support element, you can immediately select one of these elements. If you select K <n / 2, this support element will be the exact median.
Now the question is: will working with the stack break the asymptotic behavior of the algorithm? This is a very good question, because at first glance it seems that the vertices in our recursive tree are of order O (n) and for each vertex we need O (log 2 n) operations with the stack. Is the asymptotic behavior worsening to O (nlog 2 n) for our Median of Medians (and to O (nlog 3 n) for the whole algorithm)? Everything is a bit more complicated here.
To calculate the exact number of vertices in a tree, one must solve the following recurrence:
N (n) = N (n / 5) + N (7N / 10) + 1
N (n) = 1 for n
Something similar could be seen above, but replacing Cn with 1 makes the recurrent somewhat more difficult to calculate. The Acra-Bazzi method comes to the rescue . Our recurrence fits all conditions and after all the corresponding permutations we get that the number of vertices N (n) grows as O (n 0.84 ) (Θ (n 0.839780 ... ) to be more precise). Total time complexity of the algorithm is O (n + n 0.84 log 2 n) = O (n).
I consider the further spelling of the algorithm unnecessary, you just need to implement what was described in one of the previous chapters of the article. Better to look at the code. There will be no pictures either - for the algorithm to work at all, you need a rather large number of elements in the array. Which one? More about this below.
How impractical is the proposed algorithm? Here are some calculations:
Let us want to get a deviation of no more than 1 / 4n from the real median (that is, K <n / 2). Then we need to hammer the stack at 3 [logn] recursion levels (here log is binary, 3 due to the fact that (3/4) 3<0.5, and [x] is the rounding of the number x up to the nearest integer). For each recursion level, we need 2 [logn] bits - we need to store the current length of the array, which element we are looking for in order now (this number always fits into [logn] -1 bits) and one more bit to maintain the traversal tree traversal order (necessary remember which branch of recursion we returned from). For each bit, there are 2 elements, total 12 [logn] 2 elements per stack.
Now we solve the equation: 12 [logn] 2 <n / 2 or 24 [logn] 2 <n. It is necessary to find an n 'such that for any n> = n' 24 [logn] 2 <n. This n 'is of the order of 3500. That is, for n <3500 it is necessary to sort by a bubble.
The limit for n, starting from which K always does not exceed n - 1500, that is, for n <1500, sorting does not even work (there aren’t enough elements to emulate the stack), here you should use a bubble without hesitation. However, if you play around with constants, then, probably, you can improve this estimate.
Code .
All links to code throughout the article in one place:
- Runtime - Guaranteed O (nlogn).
- Using O (1) extra memory.
- Applicability for sorting data in singly linked lists (but not limited to).
Reservations for all three restrictions:
- Guaranteed O (nlogn) means that, for example, the average time for quick sorting is not suitable - O (nlogn) should be obtained for any, even the worst input.
- Recursion cannot be used because it implies O (logn) memory for storing a stack of recursive calls.
- There is no arbitrary access to the elements of the sorted array, we can move an iterator from any element only to the neighboring one (beyond O (1)), and only in one direction (forward in the list). It is impossible to modify the list itself (to outweigh pointers to the following elements).
All the information that we know about the elements of the array is that they all form a linearly ordered set . All we can do is compare two elements of the array (for O (1)) and swap them (also for O (1)).
Under the cut you can find out what happened with us.
Challenge Before you look under the cat, I suggest that you first think about the algorithm yourself. If you come up with something cooler than our option - write in the comments.
Reservations
I will make a reservation that there was no thorough search on the articles - perhaps we re-opened some already known algorithm, or the algorithm that solves this problem has long been known (perhaps much more efficient than ours).
The practical application of our algorithm is hardly possible, the task is more of academic interest.
Collection of information
Known sorts that immediately come to mind do not satisfy all three points at the same time, for example:
- Bubble Sort (bubble sort) fits under paragraphs 2 and 3, but works for O (n 2 ).
- Quick sort satisfies clauses 2 and 3 (clause 2 - with knowledge of some idea), but for clause 1 it gives O (nlogn) time only on average and there are input data on which it will work for O (n 2 ).
- Heap sorting satisfies restrictions 1 and 2, but, unfortunately, requires random access to memory.
- Merge sorting is suitable for restrictions 1 and 3, however, it requires O (n) additional memory.
- In-place merge sort fits into restrictions 1 and 2 (there is even its stable option , but it’s tin), but it is completely unclear how to effectively implement it without random access to memory.
Median of Medians or BFPRT Algorithm
In the first comment, a friend of FordPerfect proposed the Median of Medians algorithm, which was not very well known in wide circles. Other BFPRT its name from the names of scientists who invented it: Manuel B lum, Robert W. F Lloyd Vaughn R Ratt, Ronald L. P ivest and Robert E. T Arjan. The algorithm is described on Wikipedia ( ru , en ), as well as in Kormen, but I will tell you a little about it, because on Wikipedia it is described so clumsy that I understood its essence only after comparing the Russian and English versions (and I also had to look into the original article) And on Habré his description was not yet. In Cormen, if anything, the description is normal, but I learned later that this algorithm is there. If you already know this algorithm, you can skip this piece of the article.
The Median of Medians algorithm allows you to find the kth ordinal statistics on any array in linear time in the worst case. The C ++ STL library has a similar algorithm, std :: nth_element, which also finds the kth ordinal statistics for linear time, but on average, because it is based on the Quickselect algorithm. The latter is essentially a quick sort, in which at each step we go down only one branch of recursion (more about Quickselect can be read here and here) Median of Medians is a modification of the Quickselect algorithm and does not allow the selection of a bad element for "branching", which in the worst case leads to a squared time.
Why do we need this Median of Medians? Yes, everything is quite simple - with its help, you can find the median of the array (n / 2nd order statistics) in linear time and branch the fast sorting algorithm on this element. This will cause quick sort to work for O (nlogn) not on average, but in the worst case.
Description of the Median of Medians algorithm. Input data: an array (specified, for example, by the first and last elements of the list) and the number k - which account element do we need to find.
- If the array is small enough (less than 5 elements) - in the forehead we sort it with a bubble and return the k-th element.
- We break all the elements of the array into blocks of 5 elements. We are not paying attention to a possible incomplete last block.
- In each block, we sort the elements with a bubble.
- We select a subarray from the middle (third) elements of each block. You can simply move them to the beginning of the array.
- Recursively launch the Median of Medians for these [n / 5] elements and find their median (n / 10th element). This element will be called a pivot element.
- We are doing the separation procedure, probably familiar to everyone by the quick sort and quickselect algorithms: we move all elements less than the reference one to the beginning of the array, and all elements more to the end. Elements from a possible incomplete block at the end of the array are also taken into account. Total, we get three blocks: elements are less than basic, equal to it and more than it.
- We determine in which of the blocks we need to look for our kth element. If it is in the second block, we return any element from there (they are all the same all the same). Otherwise, we recursively launch the Median of Medians for this block with a possible correction for the element number: for the third block, the lengths of the previous blocks must be subtracted from the number k.
Consider what is happening here as an example. Let there be an array and we want to find its median:

There are 27 different numbers from 1 to 27. We are looking for the 14th element in a row. We divide the elements into blocks of length 5 and sort the numbers inside each block: The

medians of each block are highlighted in yellow. We move them to the beginning of the array and recursively run our algorithm to search for the median in it:

I will not paint what happens inside the recursion, one thing is clear - the desired median will be 12.

This number 12 - the supporting element or median of the medians - has the following remarkable property. Let's go back a couple of pictures and mentally move our blocks as follows:

All columns are sorted by the middle element, plus the elements in each column are also sorted. We can see that approximately 30% of the elements (3 / 10n + O (1), to be precise), which are higher and to the left of the support element, are not larger than it. Similarly, for about 30% of the elements below and to the right of the support element - they are no less than it. This means that when we carry out the separation procedure, approximately 30% of all elements will necessarily be to the left of the support element and approximately 30% to the right:

In fact, there is a slight inaccuracy: we are lucky with the fact that there are exactly one piece of elements equal to the reference one. If there are a lot of such elements, then they all form a whole block and it is not clear where exactly the supporting element will fit. But it doesn’t really matter. We know that elements that are not less than the supporting element are at least 30%, which means elements that are strictly smaller than the supporting element are not more than 70%. Similarly - elements that are strictly larger than the supporting element are also no more than 70%. Thus, the sizes of the first and third blocks from the description of the algorithm above will always have a length of not more than 7 / 10n + O (1)!

We continue the analysis of the example. After the separation procedure, it becomes clear that our 14th element is in the third block, so we recursively run the entire algorithm for it, but now we are looking for the 2nd element in it.
What is the complexity of our algorithm?
Let T (n) be the worst case number operation of the Median of Medians algorithm for an array of length n. At each step, the algorithm invokes itself twice twice. The first time is to find the median of the medians on an array of n / 5 + O (1) elements in length. The second time - reducing the search space, while in the worst case, the size of the array decreases to 7 / 10n + O (1). All other operations require linear time.
As a result, we obtain the relation: T (n) = T (2 / 10n) + T (7 / 10n) + Cn, where C is a constant.
We expand this relation:
T (n) = Cn + (2/10 + 7/10) Cn + (2/10 + 7/10) (2/10 + 7/10) Cn + ... = Cn * ∑ i = 0 ..∞ (9/10) i = 10Cn = O (n)
Great! The algorithm has linear complexity!
Median of Medians is easy to implement on lists using recursion, which gives us a good partial solution to the original problem: guaranteed sorting for O (nlogn) on a singly linked list using O (logn) memory.
Code .
Let's get rid of recursion now.
Flat quick sort
To get started, let's remove the recursion from the actual quick sort. How to do this is not entirely obvious, so in this section we will look at how to do it.
This section will describe the idea that Comrade FordPerfect suggested on the gamedev.ru forum (yes, in fact, all the ideas in this article are not mine - I just posted it). The source of the idea is unknown, Google for the most part is silent and gives a lot of links to the so-called iterative quicksort, where the stack is emulated quite often (however, there was a discussion of a similar idea), and FordPerfect says that it was invented by his classmate for 40 minutes to think about the “quicksort with O (1) memory” task. The name “Flat quick sort” is also self-made, perhaps this algorithm is known under a different name.
Let's remember how regular recursive quicksort works. Input data: an array specified, for example, by two iterators on the start and end elements of a simply connected list.
- Check in one pass: if the array is already sorted, then there is nothing to do - exit.
- We select an element (pivot) for the separation procedure - usually randomly, but for our case - the median using the Median of Medians algorithm.
- We create a separation procedure - we get three blocks: elements that are smaller than pivot; elements that are equal to him; and the elements are bigger.
- Recursively run quick sort for the first and third blocks.
The information that we need to remember during the recursion is where the third block begins and ends.
We note the following thing: any element of the first block is smaller than any element of the second block, and any element of the second block is smaller than any element of the third block.
The idea is this: let's move the largest element to the beginning of the block in each block. Then we can unambiguously determine where the next block will begin! To do this, we will just go from the beginning of the block until we meet an element strictly larger - it will signal the beginning of the next block!
Now the quick sort algorithm can be rewritten as follows:
- Create pointers X and Y. Let pointer X point to the beginning of the array and pointer Y to its end. We also create a pointer Z, which will point to the end of the current block. Initially, Z = Y.
- We endlessly perform the following actions:
- If the current XZ block is already sorted, look for the next block. We move X to the element following Z. If X cannot be moved, since Z = Y, we exit the loop. Now we are looking for the nearest element a after X, which is larger than the element that X points to. If this is not the case, do Z = Y, otherwise move Z to the element before a.
- We perform the usual actions of quick sorting: the choice of an element for separation and the separation itself. We get three blocks.
- We make blockification of the third block: we look for the maximum element in it and move it to the beginning.
- Move Z to the end of the first block.
Now let's look at this algorithm using an example:

Somewhere I already saw this array ... Let's arrange the pointers X, Y and Z:

The XZ block is not sorted. Then we find the median:

We assume that the median search procedure mixes the elements in the most bizarre way, leaving the median itself at the very beginning (for illustration purposes, an implementation may, for example, return an iterator to an element that is a median). Ok, let's now perform the separation procedure:

3 blocks are obtained. Block the last block and move Z to the end of the first block:

Now we start from the beginning. The current XZ block is not sorted, so we are looking for the median in it

:

Perform the separation procedure: Block the third block and move Z to the end of the first block:

Again look at XZ:

We are lucky! The block is sorted, so you can leave it alone and look for the next block. The X and Z pointers will move as follows:

Suddenly, this block is also sorted, since this is the second block of the previous step. We are looking for the following block: We
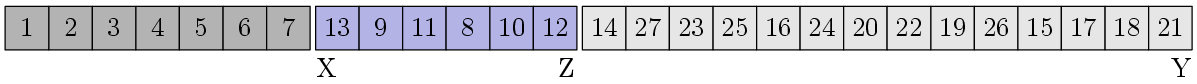
check for ordering - alas, this time we were not lucky, we have to arrange it. We find the median, and then do the separation procedure:

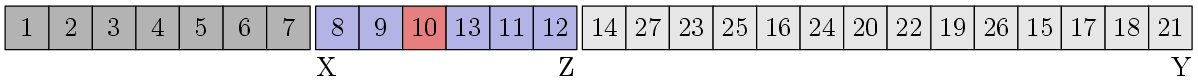
Next, we go to block [8,9], it is sorted, so X and Z will move to block [10], which is also sorted, after which the algorithm will consider the block [13, 11, 12], in which everything is already completely trivial. Sorting analysis of the second half of the array is proposed to be performed by the reader independently.
Code .
Approximate Median of Medians with O (1) Extra Memory
Unfortunately, with Median of Medians, such a trick as using the maximum element to identify blocks in flat quick sort will not work, because the elements of the array each time are mixed in unclear how. Here we will use a different focus.
In fact, to make quick sort work for guaranteed O (nlogn), it is not necessary to find the exact median for the split stage. It is enough to find something approximate. If we guarantee that the first and third blocks after the separation stage will not exceed Cn for some specific C <1, quick sort will work for O (nlogn). Even for C = 0.99. With a
Therefore, we modify the Median of Medians so that it finds the median with some error K = O (log 2n). That is, an element will be found whose serial number is somewhere in the range from n / 2-K / 2 to n / 2 + K / 2. Since K is of the order of the degree of the logarithm, it is easy to find such a (concrete) n starting from which the segment [n / 2-K / 2, n / 2 + K / 2] lies, say, between 1 / 4n and 3 / 4n. For all smaller n, you can sort by just a bubble.
Why is K = O (log 2 n)? Yes, we just use K array elements in order to store in them all the necessary information on the stack (the idea, again, is FordPerfect comrade). The recursion levels are O (logn), on each of them we need to store O (1) numbers per O (logn) bit. And find the median for quick sort among the remaining NK elements.
Each bit is represented by two consecutive different elements of the array. If the first of them is less than the second, the bit stores the state 0, otherwise - 1 (or vice versa). The first task that we need to solve is to find K / 2 pairs of different elements of the array and understand what to do if so many pairs are not found.
This is done very simply. Let the iterators X and Y point to the first element of the array. We will move Y forward until we find an element that is not equal to X. If you find it, move X forward, swap the elements that X and Y point to, move X forward again (+ you still need to handle the small case - move Y forward if faced X). And so until we find K / 2 pairs. What if Y has already reached the end of the array and K / 2 pairs have not yet been found? This means that all elements from X to Y inclusive are the same! (It is quite simple to verify that this invariant is preserved throughout the execution of the entire algorithm). Then, as a support element, you can immediately select one of these elements. If you select K <n / 2, this support element will be the exact median.
Now the question is: will working with the stack break the asymptotic behavior of the algorithm? This is a very good question, because at first glance it seems that the vertices in our recursive tree are of order O (n) and for each vertex we need O (log 2 n) operations with the stack. Is the asymptotic behavior worsening to O (nlog 2 n) for our Median of Medians (and to O (nlog 3 n) for the whole algorithm)? Everything is a bit more complicated here.
To calculate the exact number of vertices in a tree, one must solve the following recurrence:
N (n) = N (n / 5) + N (7N / 10) + 1
N (n) = 1 for n
Something similar could be seen above, but replacing Cn with 1 makes the recurrent somewhat more difficult to calculate. The Acra-Bazzi method comes to the rescue . Our recurrence fits all conditions and after all the corresponding permutations we get that the number of vertices N (n) grows as O (n 0.84 ) (Θ (n 0.839780 ... ) to be more precise). Total time complexity of the algorithm is O (n + n 0.84 log 2 n) = O (n).
I consider the further spelling of the algorithm unnecessary, you just need to implement what was described in one of the previous chapters of the article. Better to look at the code. There will be no pictures either - for the algorithm to work at all, you need a rather large number of elements in the array. Which one? More about this below.
How impractical is the proposed algorithm? Here are some calculations:
Let us want to get a deviation of no more than 1 / 4n from the real median (that is, K <n / 2). Then we need to hammer the stack at 3 [logn] recursion levels (here log is binary, 3 due to the fact that (3/4) 3<0.5, and [x] is the rounding of the number x up to the nearest integer). For each recursion level, we need 2 [logn] bits - we need to store the current length of the array, which element we are looking for in order now (this number always fits into [logn] -1 bits) and one more bit to maintain the traversal tree traversal order (necessary remember which branch of recursion we returned from). For each bit, there are 2 elements, total 12 [logn] 2 elements per stack.
Now we solve the equation: 12 [logn] 2 <n / 2 or 24 [logn] 2 <n. It is necessary to find an n 'such that for any n> = n' 24 [logn] 2 <n. This n 'is of the order of 3500. That is, for n <3500 it is necessary to sort by a bubble.
The limit for n, starting from which K always does not exceed n - 1500, that is, for n <1500, sorting does not even work (there aren’t enough elements to emulate the stack), here you should use a bubble without hesitation. However, if you play around with constants, then, probably, you can improve this estimate.
Code .
The code
All links to code throughout the article in one place:
- Quick sort + Median of Medians (Guaranteed O (nlogn), O (logn) extra memory)
- Flat quick sort + Median of Medians (Guaranteed O (nlogn), O (logn) additional memory)
- Flat quick sort + Approximate Median of Medians (Guaranteed O (nlogn), O (1) extra memory)
Read
- Discussion of the algorithm on gamedev.ru.
- Median of Medians on Wikipedia ( en , ru ).
- You can read about Quickselect here and here .
- Acra-Bazzi method on Wikipedia.
- Manual Blum, Robert W. Floyd, Vaughan Pratt, Ronald L. Rivest, and Robert E. Tarjan. Time Bounds for Selection . (pdf, eng)
- S.Battiato, D.Cantone, D.Catalano and G.Cincotti. An Efficient Algorithm for the Approximate Median Selection Problem . (pdf, eng) - Fast approximate probabilistic Median of Medians
