Fractals, Fortran, and OpenMP
Once upon a time I decided to “touch” Fortran. The only task I came up with is the generation of fractals (at the same time, OpenMP in Fortran could be tried). In the process of writing, I often came across problems whose solution I had to think for myself (for example, there are not many examples of using double-precision numbers or binary writing to a file on the Internet). But sooner or later all the problems were resolved, and I want to write this text, which will probably help someone.
I will write in the Fortran 90 dialect, but with GNU extensions (the same double-precision numbers).
A fractal ( fractus - crushed, broken, broken) - in the narrow sense, a complex geometric figure that has the property of self-similarity, that is, composed of several parts, each of which is similar to the whole figure.
There is a large group of fractals - algebraic fractals. This name follows from the principle of constructing such fractals. To build them, use recursive functions. For example, algebraic fractals are: Julia Set, Mandelbrot Set, Newton's Pool (fractal).
One of the construction methods is an iterative calculation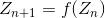
, where 
, and a 
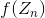certain function. The calculation of this function continues until a certain condition is met. When this condition is met, a dot is displayed.
The behavior of the function for different points of the complex plane can have different behavior:
One of the simplest (both for understanding and for implementing) algorithms for constructing algebraic fractals is known as the " escape time algorithm ". In short, iteratively calculates the number for each point of the complex plane.
It has been proven that if there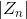
is more bailout , then the sequence 
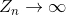. Comparison with bailout allows you to find points lying outside the set. For points lying outside the set, the sequence 
will not tend to infinity, so it will never reach bailout .
I will consider two simple fractals - the Julia Set and the Mandelbrot Set. They are calculated according to the same function, but differ only in a constant, where for Julia it is a constant constant, and for Mandelbrob the constant depends on a point on the complex plane.
The beginning and end of the program is simple and trivial:
Next we need to introduce several constants:
And here you need to explain something. REAL and COMPLEX are a single precision floating point number and a complex number consisting of two REALs . REAL (8) is a double precision number, and COMPLEX (8) , respectively, is a complex number consisting of two REAL (8) . The letter D is also added to the standard functions (as is the case with ABS ), which indicates the use of double-precision numbers.
Next we need to introduce several variables:
Using ALLOCATABLE is required! Because otherwise:
The memory we have allocated on the stack, and this is not acceptable when used in multiple threads. Therefore, we allocate memory on the heap.
So I do not use two-dimensional arrays, because when allocating on the heap, the array will take up more space, and it will be more difficult to write it to a file.
Next, we need to specify the number of threads generated by OpenMP:
And here the calculations begin directly. In Fortran, directives for OpenMP are specified through comments (in C / C ++ there is a special macro #pragma for this).
The most time-consuming part is over. Further, it remains for us to display information in a convenient form for perception - an image. I will use the PNM format, as This is the easiest image format.
PNM consists of several sections:
The first line is an indication of the format for recording pixel information:
The first P is an option where the pixel color is written in ASCII character, and the second P makes it possible to record the pixel color in binary form (which significantly saves disk space).
The next line is a comment, then the image resolution and the number of colors per pixel. After the number of colors, information about the pixels comes directly.
We begin to write the image to a file:
We perform DEALLOCATE for decency, because when you exit the program, the OS will still return the occupied memory to the system.
To build the program, you can use the GNU compiler - gfortran:
You should get the following image:
This is easy to do, just replace c and change a few constants. In this case, remove the constant c and add the variable c :
And also change the old constants:
You should get the following image:
upd
After I worked in Ada, I found one error - where I used Mod . This function played the role of a crutch for me, because we have a color channel takes values from 0 to 255, it turned out that I made Mod 'ohm so that the value was not higher than the maximum. As you can see in the images, this leads to sharp transitions in colors.
I will correct it by using the formula:
. It turns out a variation of linear interpolation in linear space.
To make it easier to use, we will write the following function:
And replace the color assignment to the dots:
The following image is obtained:
upd2
Since in Fortran, as well as in Ada, EOL is automatically selected, then under non-Unix PNM systems it turns out to be wrong. To avoid this, you will have to use the following bike:
en.wikipedia.org/wiki/Fractal
en.wikipedia.org/wiki/Julia_set
en.wikipedia.org/wiki/Mandelbrot_set
en.wikipedia.org/wiki/OpenMP
openmp.org/wp/openmp-specifications
gcc.gnu.org / onlinedocs / gfortran
I will write in the Fortran 90 dialect, but with GNU extensions (the same double-precision numbers).
A bit of fractal theory
A fractal ( fractus - crushed, broken, broken) - in the narrow sense, a complex geometric figure that has the property of self-similarity, that is, composed of several parts, each of which is similar to the whole figure.
There is a large group of fractals - algebraic fractals. This name follows from the principle of constructing such fractals. To build them, use recursive functions. For example, algebraic fractals are: Julia Set, Mandelbrot Set, Newton's Pool (fractal).
Construction of algebraic fractals
One of the construction methods is an iterative calculation
, where , and a certain function. The calculation of this function continues until a certain condition is met. When this condition is met, a dot is displayed. The behavior of the function for different points of the complex plane can have different behavior:
- Tends to infinity
- Tends to 0
- It takes several fixed values and does not go beyond them.
- Chaotic behavior. The absence of any trends
One of the simplest (both for understanding and for implementing) algorithms for constructing algebraic fractals is known as the " escape time algorithm ". In short, iteratively calculates the number for each point of the complex plane.
It has been proven that if there
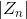is more bailout , then the sequence 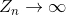. Comparison 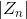with bailout allows you to find points lying outside the set. For points lying outside the set, the sequence will not tend to infinity, so it will never reach bailout .I will consider two simple fractals - the Julia Set and the Mandelbrot Set. They are calculated according to the same function, but differ only in a constant, where for Julia it is a constant constant, and for Mandelbrob the constant depends on a point on the complex plane.
Building the Julia Set
The beginning and end of the program is simple and trivial:
program frac
end
Next we need to introduce several constants:
INTEGER, PARAMETER :: iterations = 2048 !Количество итераций. Чем больше, тем глубже будет идти просчет
REAL(8), PARAMETER :: mag_ratio = 1.0_8 !Приближение
REAL(8), PARAMETER :: x0 = 0.0_8 !Смещение комплексной плоскости
REAL(8), PARAMETER :: y0 = 0.0_8 !
INTEGER, PARAMETER :: resox = 1024 !Разрешение получившегося изображения
INTEGER, PARAMETER :: resoy = resox
REAL(8), PARAMETER :: xshift = (-1.5_8 / mag_ratio) + x0 !Смещение центра комплексной оси в
REAL(8), PARAMETER :: yshift = (-1.5_8 / mag_ratio) + y0 !центр изображения
REAL(8), PARAMETER :: CXmin = -1.5_8 / mag_ratio !Следующие константы растягивают
REAL(8), PARAMETER :: CXmax = 1.5_8 / mag_ratio !комплексную плоскость до размеров resox x resoy
REAL(8), PARAMETER :: CXshag = (DABS(CXmin) + DABS(CXmax)) / resox !Связываем значение одного пикселя и точки на комплексной плоскости
REAL(8), PARAMETER :: CYmin = -1.5_8 / mag_ratio
REAL(8), PARAMETER :: CYmax = 1.5_8 / mag_ratio
REAL(8), PARAMETER :: CYshag = (DABS(CYmin) + DABS(CYmax)) / resoy
COMPLEX(8), PARAMETER :: c = DCMPLX(0.285_8, 0.01_8) !Наша основная константа
And here you need to explain something. REAL and COMPLEX are a single precision floating point number and a complex number consisting of two REALs . REAL (8) is a double precision number, and COMPLEX (8) , respectively, is a complex number consisting of two REAL (8) . The letter D is also added to the standard functions (as is the case with ABS ), which indicates the use of double-precision numbers.
Next we need to introduce several variables:
CHARACTER, DIMENSION(:), ALLOCATABLE :: matrix !Массив точек
COMPLEX(8) :: z
INTEGER :: x, y, iter
REAL(8) :: iter2 !Понадобится нам для сглаживания
ALLOCATE(matrix(0 : resox * resoy * 3))
Using ALLOCATABLE is required! Because otherwise:
CHARACTER, DIMENSION(0:resox * resoy * 3) :: matrix !Массив точек
The memory we have allocated on the stack, and this is not acceptable when used in multiple threads. Therefore, we allocate memory on the heap.
So I do not use two-dimensional arrays, because when allocating on the heap, the array will take up more space, and it will be more difficult to write it to a file.
Next, we need to specify the number of threads generated by OpenMP:
call omp_set_num_threads(16)
And here the calculations begin directly. In Fortran, directives for OpenMP are specified through comments (in C / C ++ there is a special macro #pragma for this).
!$OMP PARALLEL DO PRIVATE(iter, iter2, z)
do x = 0, resox-1
do y = 0, resoy-1
iter = 0 !Обнуляем количество итераций
z = DCMPLX(x * CXshag + xshift, y * CYshag + yshift) !Задаем Z начальное значение
do while ((iter .le. iterations) .and. (CDABS(z) .le. 4.0_8)) !Обычно за bailout берут 2, но я взял 4, т.к. результат лучше сглаживается
z = z**2 + c
iter = iter + 1
end do
iter2 = DFLOAT(iter) - DLOG(DLOG(CDABS(z))) / DLOG(2.0_8) !Формула для сглаживания iter-log2(ln(|Z|))
matrix((x + y * resox) * 3 + 0) = CHAR(NINT(DMOD(iter2 * 7.0_8, 256.0_8))) !Один из способов расскрашивания
matrix((x + y * resox) * 3 + 1) = CHAR(NINT(DMOD(iter2 * 14.0_8, 256.0_8)))
matrix((x + y * resox) * 3 + 2) = CHAR(NINT(DMOD(iter2 * 2.0_8, 256.0_8)))
end do
end do
!$OMP END PARALLEL DO
The most time-consuming part is over. Further, it remains for us to display information in a convenient form for perception - an image. I will use the PNM format, as This is the easiest image format.
PNM consists of several sections:
P6
#Комментарий
1024 1024
255
The first line is an indication of the format for recording pixel information:
- P1 / P4 - black and white image
- P2 / P5 - gray image
- P3 / P6 - color image
The first P is an option where the pixel color is written in ASCII character, and the second P makes it possible to record the pixel color in binary form (which significantly saves disk space).
The next line is a comment, then the image resolution and the number of colors per pixel. After the number of colors, information about the pixels comes directly.
We begin to write the image to a file:
open(unit=8, status = 'replace', file = trim("test.pnm"))
write(8, '(a)') "P6" !(a) это текстовая строка
write(8, '(a)') ""
write(8, '(I0, a, I0)') resox, ' ', resoy
write(8, '(I0)') 255
write(8, *) matrix
close(8)
DEALLOCATE(matrix)
We perform DEALLOCATE for decency, because when you exit the program, the OS will still return the occupied memory to the system.
To build the program, you can use the GNU compiler - gfortran:
gfortran -std=gnu frac.f90 -o frac.run -fopenmp
You should get the following image:
1024x1024
How to Generate a Mandelbrot Set
This is easy to do, just replace c and change a few constants. In this case, remove the constant c and add the variable c :
COMPLEX(8) :: z, c
z = DCMPLX(x * CXshag + xshift, y * CYshag + yshift) !Задаем Z начальное значение
c = z
And also change the old constants:
INTEGER, PARAMETER :: MAIN_RES = 1024
INTEGER, PARAMETER :: resox = (MAIN_RES / 3) * 3
INTEGER, PARAMETER :: resoy = (resox * 2) / 3
REAL(8), PARAMETER :: xshift = (-2.0_8 / mag_ratio) + x0
REAL(8), PARAMETER :: yshift = (-1.0_8 / mag_ratio) + y0
REAL(8), PARAMETER :: CXmin = -2.0_8 / mag_ratio
REAL(8), PARAMETER :: CXmax = 1.0_8 / mag_ratio
REAL(8), PARAMETER :: CXshag = (DABS(CXmin) + DABS(CXmax)) / resox
REAL(8), PARAMETER :: CYmin = -1.0_8 / mag_ratio
REAL(8), PARAMETER :: CYmax = 1.0_8 / mag_ratio
REAL(8), PARAMETER :: CYshag = (DABS(CYmin) + DABS(CYmax)) / resoy
You should get the following image:
1023x682
upd
After I worked in Ada, I found one error - where I used Mod . This function played the role of a crutch for me, because we have a color channel takes values from 0 to 255, it turned out that I made Mod 'ohm so that the value was not higher than the maximum. As you can see in the images, this leads to sharp transitions in colors.
I will correct it by using the formula:
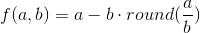. It turns out a variation of linear interpolation in linear space. To make it easier to use, we will write the following function:
function myround(a) result(ret)
REAL(8), intent(in) :: a
INTEGER :: ret !Для удобства мы сразу взяли b как 255, сразу приводим к INTEGER и убираем знак.
ret = ABS(INT(a - 255.0_8 * NINT(a / 255.0_8))) !NINT() это функция аналогичная round() в C, т.е. округляем к ближайшему целому
end function myround
program frac
INTEGER :: myround
And replace the color assignment to the dots:
matrix((x + y * resox) * 3 + 0) = CHAR(myround(iter2 * 7.0_8))
matrix((x + y * resox) * 3 + 1) = CHAR(myround(iter2 * 14.0_8))
matrix((x + y * resox) * 3 + 2) = CHAR(myround(iter2 * 2.0_8))
The following image is obtained:
1024x1024
upd2
Since in Fortran, as well as in Ada, EOL is automatically selected, then under non-Unix PNM systems it turns out to be wrong. To avoid this, you will have to use the following bike:
write(8, '(a, a, $)') "P6", char(10)
write(8, '(a,$)') char(10)
write(8, '(I0, a, I0, a, $)') resox, ' ', resoy, char(10)
write(8, '(I0, a, $)') 255, char(10)
write(8, *) matrix
Used Books
en.wikipedia.org/wiki/Fractal
en.wikipedia.org/wiki/Julia_set
en.wikipedia.org/wiki/Mandelbrot_set
en.wikipedia.org/wiki/OpenMP
openmp.org/wp/openmp-specifications
gcc.gnu.org / onlinedocs / gfortran