How is Data Matrix created?
 Data Matrix is a two-dimensional matrix barcode consisting of light and dark areas. Using this barcode, you can encode a fairly large amount of information (2-3Kb). Often, Data Matrix is used in the labeling of small items, such as microcircuits, as well as in the food and defense industries, advertising and other fields.
Data Matrix is a two-dimensional matrix barcode consisting of light and dark areas. Using this barcode, you can encode a fairly large amount of information (2-3Kb). Often, Data Matrix is used in the labeling of small items, such as microcircuits, as well as in the food and defense industries, advertising and other fields. There are many sites for creating such codes, but I was always wondering how the text turns into a set of black and white squares. Should there be some kind of algorithm?
When creating the Data Matrix, we need to turn to the arithmetic of Galois fields and Reed-Solomon codes. Consider this process with a simple example.
First of all, let's look at the structure of the matrix:

Our matrix consists of two parts: a search pattern and encoded data. Of course, the size of the matrix is directly proportional to the size of the input data. Around our code, there must be a free zone separating the code from the rest of the image.
Take a short word, for example, “Habr” (without quotes) and create a Data Matrix for it. The process consists of two stages: at the high-level coding stage, you need to obtain a sequence of data codes and error correction codes, and at the low-level coding stage, you need to depict a binary representation of these codes in the matrix.
High level coding
In the Data Matrix, as in the QR code, Reed-Solomon codes are used above the Galois field
 (the number 8 is selected, since each codeword occupies 8 bits in the matrix). There are several irreducible polynomials that allow such a field to be generated. Among them
(the number 8 is selected, since each codeword occupies 8 bits in the matrix). There are several irreducible polynomials that allow such a field to be generated. Among them 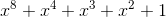 (in decimal 285, used for QR codes) and
(in decimal 285, used for QR codes) and 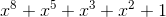 (301, used in Data Matrix).
(301, used in Data Matrix). For calculations, we need a table of powers of two for each element of the field. This table is created quite simply: if the exponent
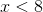 , then exponentiation is performed as usual. Otherwise
, then exponentiation is performed as usual. Otherwise  , after which bitwise addition modulo 2 is performed with a decimal representation of the taken irreducible polynomial if
, after which bitwise addition modulo 2 is performed with a decimal representation of the taken irreducible polynomial if  . For example
. For example  ,
,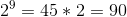 etc.
etc. It is necessary to obtain a codeword
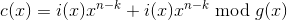 ,
, where
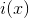 is the information polynomial,
is the information polynomial,  is the generating polynomial,
is the generating polynomial, 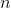 is the total length of the code along with the corrective ones,
is the total length of the code along with the corrective ones, 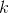 is the number of information codes (together with the indent codes, about them later),
is the number of information codes (together with the indent codes, about them later),  is the operation of taking the remainder of the division.
is the operation of taking the remainder of the division. First, we create an information polynomial. To do this, we need to know what size the matrix should be so that all information codes can be placed:

From the table it can be seen that to encode a row of 4 elements, we need to take a 12x12 matrix (“useful” area is 10x10), which contains 5 codes data and 7 correction codes.
For ASCII table characters, the code is as follows: C = ASCII value + 1. For example, for the character 'H' C = 72 + 1 = 73.
The running numbers are combined in pairs, and for them C = N + 130, where N is the number obtained as a result of grouping. For example, if the numbers 2 and 5 are nearby, then C = 25 + 130 = 155.
Since we have fewer elements than it should be (instead of five, only four), you need to add special indent codes. The first such code is always 129. The subsequent indent codes, up to the first error correction code, are calculated as follows:,
 where
where 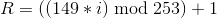 is the pseudo-random number,
is the pseudo-random number,  is the number of the element.
is the number of the element. For the word “Habr” we get the following sequence of codes: 73, 98, 99, 115, 129.
Now we can write the information polynomial:
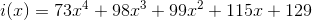
and multiply it by
 (
(  - the number of correction codes):
- the number of correction codes): 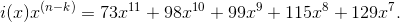
We now proceed to create the generating polynomial. It is calculated by the following formula:
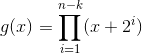
We start to multiply the brackets:
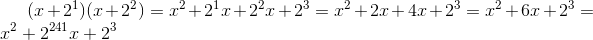

Addition in our field is defined as bitwise addition modulo 2. First, raising to a power using a table is performed, then adding them and finding the “logarithm” of the resulting number to return to powers of two. If, after adding the degrees, a number greater than 254 is obtained, take its remainder from dividing by
 .
. After multiplying all the brackets and raising to the power we get:

The last operation that completes the high-level coding, and perhaps the most difficult, is finding the remainder of the division
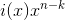 by
by  :
: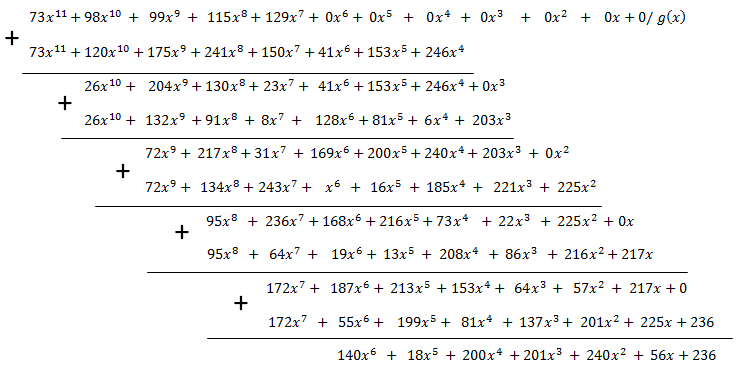
The polynomials are divided into columns, but taking into account the fact that the subtraction defined in the same way as addition and multiplication are performed in the Galois field.
Now we can write the codeword
 completely:
completely:
Low level coding
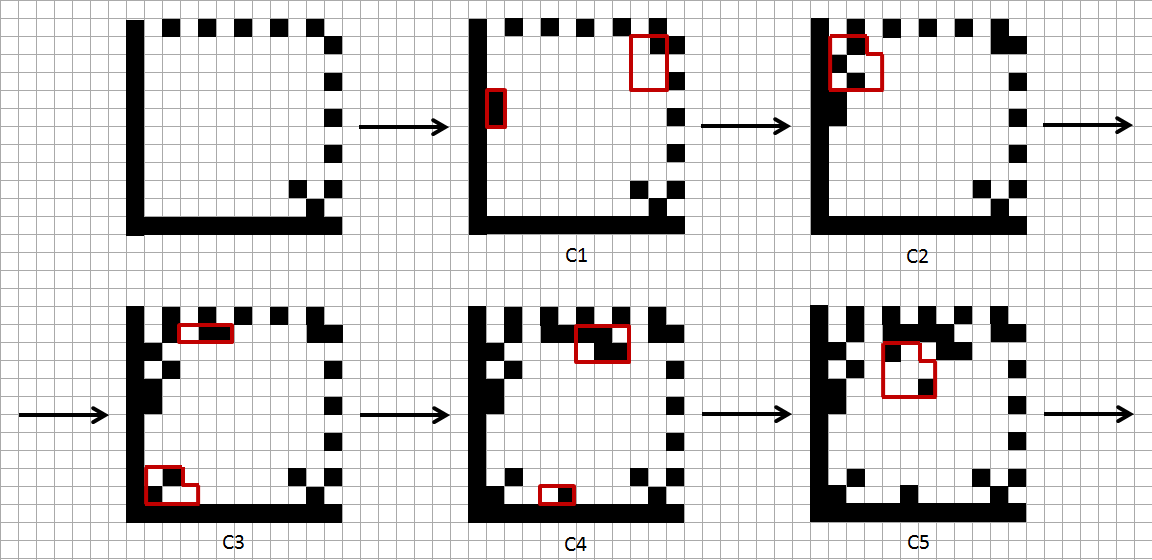
 Each of the codes obtained above is represented in the Data Matrix as a square of 3x3 cells without the upper right corner. 1 here corresponds to the most significant bit, 8 - to the least significant. It is necessary to fill the entire matrix with such elements.
Each of the codes obtained above is represented in the Data Matrix as a square of 3x3 cells without the upper right corner. 1 here corresponds to the most significant bit, 8 - to the least significant. It is necessary to fill the entire matrix with such elements.  We will prepare a 10x10 grid (this is exactly the size the matrix should be in this case), on which we will draw the contours of the first five elements, as in the figure on the right. Regardless of how large the matrix is, these elements are always located exactly this way, and nothing else.
We will prepare a 10x10 grid (this is exactly the size the matrix should be in this case), on which we will draw the contours of the first five elements, as in the figure on the right. Regardless of how large the matrix is, these elements are always located exactly this way, and nothing else. The remaining elements are placed in a similar way, but before drawing them, it is necessary to note several special cases associated with the corners of the matrix.
If
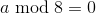 , where a is the side of the square, then we have the simplest case when, after placing all the elements, the non-placed sections are simply transferred to the opposite side.
, where a is the side of the square, then we have the simplest case when, after placing all the elements, the non-placed sections are simply transferred to the opposite side. If
 , then in the lower right corner there remains an “extra” 2x2 square, which is filled as follows:
, then in the lower right corner there remains an “extra” 2x2 square, which is filled as follows:
If
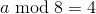 or
or  , then you should pay attention to the lower left and upper right corner, especially to the numbering of bits:
, then you should pay attention to the lower left and upper right corner, especially to the numbering of bits: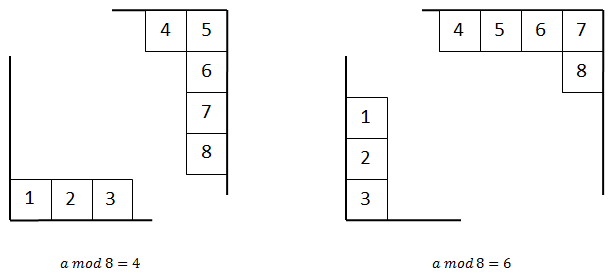
There are two more cases that arise only when constructing rectangular matrices, so we omit them.
Let's go back to our matrix and add all the other elements, and also indicate which codeword each element corresponds to. The arrows show how the numbering is done:
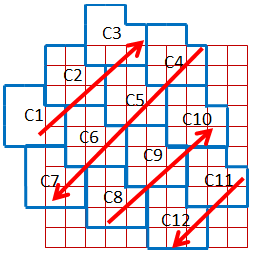
After transferring the non-placed elements, we get:
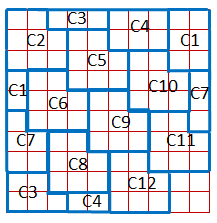
In the lower right corner there was an unoccupied square (
 which just corresponds to this case). We list all our codes in the same order in which they go in
which just corresponds to this case). We list all our codes in the same order in which they go in  , and their binary representations:
, and their binary representations:
Carefully fill the matrix. Let's start with the search template and the bottom square, and then we add each code in turn:
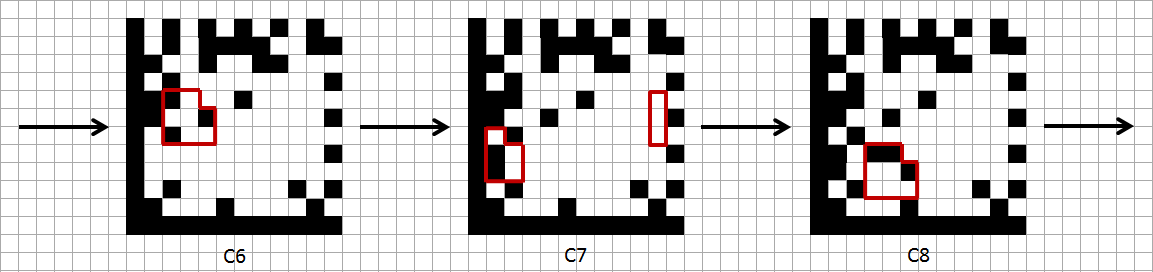


So, our Data Matrix code is ready:

