Math drawings
In this post I will give some drawings drawn using mathematical formulas. The purpose of these drawings is not just to draw something on the screen (there is computer graphics for this), but to offer a simple formula that defines the picture.

The first picture shows a lotus. The picture is built in the program Wolfram Mathematica.
These formulas are easier to imagine in a spherical coordinate system: radius vector length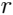 , latitude
, latitude 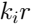 , longitude
, longitude  . The parameter is entered here
. The parameter is entered here  . Its meaning is that we take a point with longitude
. Its meaning is that we take a point with longitude  and step back from it
and step back from it  in the direction of decreasing and increasing longitude.
in the direction of decreasing and increasing longitude.
The next drawing is a pretty flower. The formula is given in a spherical coordinate system, and a compression transformation along the z axis has also been made .

Here is another flower.

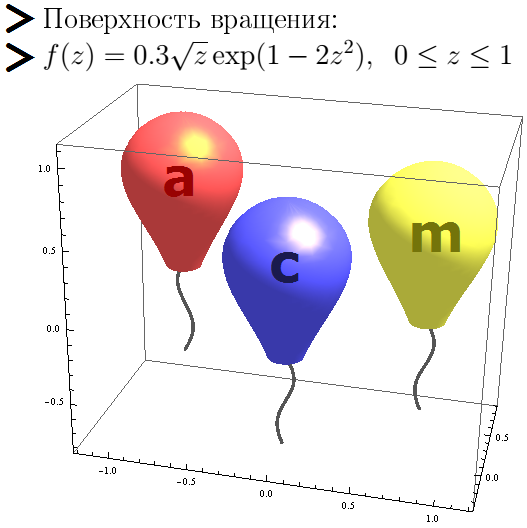
This figure shows the balls obtained as a surface of revolution for some function.
The figure reminds of the ACM programming world team championship, the quarter finals of which take place in the fall. (At the finals of this championship, the team is given a ball for a correctly solved problem.)
Now I will give a few holiday drawings.
Here is a drawing made for the New Year. This is a Christmas tree built with the help of segments.

This is a star made on February 23rd.
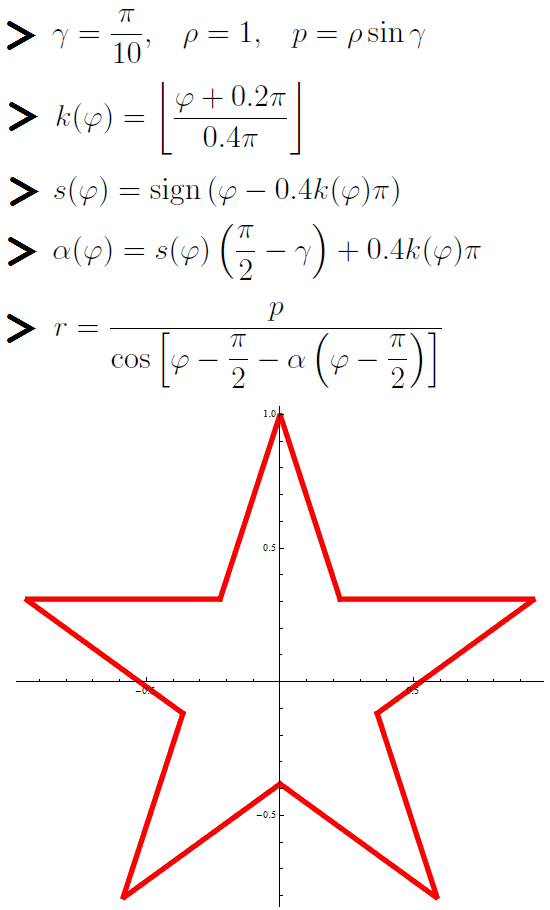
The asterisk is set using the polar equation of the line.
By the way, the parameter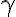 (half the angle of the star’s ray) can be varied. This star corresponds to the value
(half the angle of the star’s ray) can be varied. This star corresponds to the value 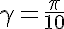 .
.
When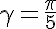 we get an asterisk similar to a starfish:
we get an asterisk similar to a starfish:

When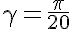 we get a spiky star:
we get a spiky star:

Here is a picture that fits on Valentine's Day.

You can even make a mathematical recognition:

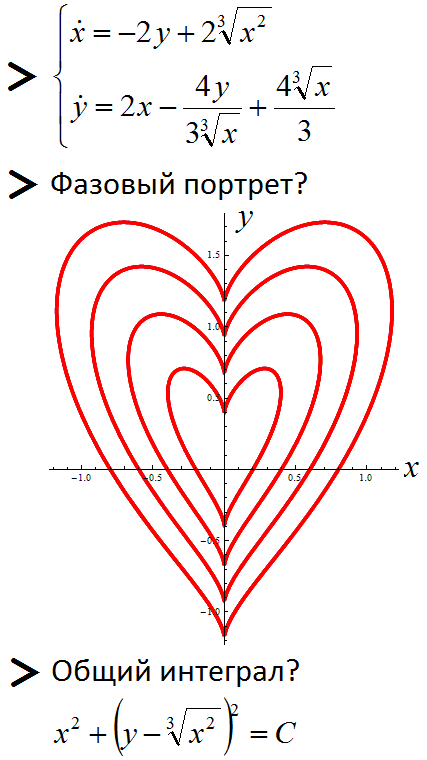
And here is another mathematical heart. An autonomous system of 2 differential equations of the first order is considered. The phase portrait of this system is constructed (the trajectories of the system are drawn under various initial conditions) and the general integral of the system is found.
This system can be obtained by differentiating the general integral with respect to t. In this way (solving a system of differential equations), it is possible to construct graphs of equations.
And this is a mathematical card for March 8th. The figure shows a certain abstract computer, which built a graph of Bernoulli's lemniscata.

The figure shows the St. George Mobius strip by May 9th.
The following figure depicts a square academic cap, the figure is suitable for September 1.

This figure shows the FEFU logo:
Here is the logo itself:

And this is the three-dimensional FEFU logo, which is also built using mathematical formulas in the Wolfram Mathematica package.


The first picture shows a lotus. The picture is built in the program Wolfram Mathematica.
The code
phi = 0;
dphi = 2*Pi/7;
theta[r_] := 0.4*r;
theta1[r_] := 1*r;
theta2[r_] := 0.7*r;
Show[
ParametricPlot3D[{r*Cos[phi], r*Sin[phi], 0}, {r, 0, 0.8}, {phi, 0,
2 Pi}, PlotStyle -> Darker[Green], Mesh -> None],
ParametricPlot3D[{r*Cos[phi], r*Sin[phi], 0.02}, {r, 0, 0.15}, {phi,
0, 2 Pi}, PlotStyle -> Yellow, Mesh -> None],
ParametricPlot3D[
Join[
Table[
{r*Cos[theta[r]]*Cos[(i*dphi) + t*dphi/2*r*(1 - r)^1.5*5],
r*Cos[theta[r]]*Sin[(i*dphi) + t*dphi/2*r*(1 - r)^1.5*5],
r*Sin[theta[r]]}, {i, 0, 6}],
Table[{r*Cos[theta1[r]]*Cos[(i*dphi) + t*dphi/2*r*(1 - r)^1.5*5],
r*Cos[theta1[r]]*Sin[(i*dphi) + t*dphi/2*r*(1 - r)^1.5*5],
r*Sin[theta1[r]]}, {i, 0, 6}],
Table[{r*Cos[theta2[r]]*
Cos[(dphi/2 + i*dphi) + t*dphi/2*r*(1 - r)^1.5*5],
r*Cos[theta2[r]]*
Sin[(dphi/2 + i*dphi) + t*dphi/2*r*(1 - r)^1.5*5],
r*Sin[theta2[r]]}, {i, 0, 6}]],
{r, 0, 1}, {t, -1, 1},
PlotStyle ->
Directive[Specularity[RGBColor[1, 0.3, 0], 20],
RGBColor[0.972, 0.658, 0.898],
Lighting -> {{"Directional",
Darker[White, 0.5], {2, 0, 2}}, {"Ambient", Darker[White]}}],
Mesh -> None],
PlotRange -> {{-0.85, 0.85}, {-0.85, 0.85}, {0, 0.8}}]
These formulas are easier to imagine in a spherical coordinate system: radius vector length
 , latitude
, latitude 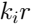 , longitude
, longitude  . The parameter is entered here
. The parameter is entered here  . Its meaning is that we take a point with longitude
. Its meaning is that we take a point with longitude  and step back from it
and step back from it  in the direction of decreasing and increasing longitude.
in the direction of decreasing and increasing longitude. The next drawing is a pretty flower. The formula is given in a spherical coordinate system, and a compression transformation along the z axis has also been made .
The code
r[theta_, phi_] :=
If[(Pi/2 - Abs[theta] < Pi/8), 0.25*Sin[theta],
Sin[4*phi]*Cos[4*theta]];
Show[ParametricPlot3D[
{r[theta, phi]*Cos[theta]*Cos[phi],
r[theta, phi]*Cos[theta]*Sin[phi],
r[theta, phi]*Sin[theta]/Sqrt[3]},
{theta, -Pi/2, Pi/2}, {phi, 0, 2*Pi}, Mesh -> None,
PlotStyle -> Orange, PlotRange -> All, MaxRecursion -> 4],
SphericalPlot3D[0.16, theta, phi, Mesh -> None, PlotStyle -> Yellow]]

Here is another flower.
The code
xx[t_] := 0;
yy[t_] := -0.75 t*(1 - t);
zz[t_] := -3 t;
rr = 0.05;
x1[t_] := 0;
y1[t_] := -0.15 + 0.5 t;
z1[t_] := -1.6 + 0.5 t;
r[theta_, phi_] :=
If[(Pi/2 - Abs[theta] < Pi/8), 0.25*Sin[theta],
Sin[4*phi]*Cos[4*theta]];
Show[ParametricPlot3D[
{r[theta, phi]*Cos[theta]*Cos[phi],
r[theta, phi]*Cos[theta]*Sin[phi],
r[theta, phi]*Sin[theta]/Sqrt[3]},
{theta, -Pi/2, Pi/2}, {phi, 0, 2*Pi}, Mesh -> None,
PlotStyle -> Orange, PlotRange -> All, MaxRecursion -> 4],
SphericalPlot3D[0.16, theta, phi, Mesh -> None, PlotStyle -> Yellow],
ParametricPlot3D[{xx[t] + rr*Cos[phi], yy[t] + rr*Sin[phi], zz[t]},
{t, 0, 1}, {phi, 0, 2 Pi}, Mesh -> None, PlotStyle -> Green],
ParametricPlot3D[{x1[t] + phi*t*(1 - t), y1[t] - 0.5 phi*t*(1 - t)^3,
z1[t]},
{t, 0, 1}, {phi, -1, 1}, Mesh -> None, PlotStyle -> Green],
Boxed -> False, Axes -> None]

This figure shows the balls obtained as a surface of revolution for some function.
The code
x1 = 0; y1 = 0; z1 = -0.2;
x2 = 0.8; y2 = 0.3; z2 = 0;
x3 = -0.8; y3 = 0.5; z3 = 0.1;
f[z_] := z*(1 - z);
f[z_] := 0.3 z^0.5*Exp[1 - 2 z^2];
gz[t_] := -0.6 t;
gy[t_] := 0.1 t*(1 - t);
gx[t_] := 0.05 Sin[6 t];
Show[ParametricPlot3D[{x1 + f[1 - z]*Cos[phi], y1 + f[1 - z]*Sin[phi],
z1 + z}, {z, 0, 1}, {phi, 0, 2*Pi},
PlotStyle ->
Directive[Specularity[RGBColor[1, 0.8, 0], 30], Lighter[Blue],
Lighting -> {{"Directional", White, {1.5, 0, 3}}, {"Ambient",
Darker[White]}}], Mesh -> None],
ParametricPlot3D[{x1 + gx[t], y1 + gy[t], z1 + gz[t]}, {t, 0, 1},
PlotStyle -> Directive[Thickness[0.0075], Lighter[Black]]],
ParametricPlot3D[{x2 + f[1 - z]*Cos[phi], y2 + f[1 - z]*Sin[phi],
z2 + z}, {z, 0, 1}, {phi, 0, 2*Pi},
PlotStyle ->
Directive[Specularity[RGBColor[1, 0.8, 0], 30], Lighter[Yellow],
Lighting -> {{"Directional", White, {1.5, 0, 3}}, {"Ambient",
Darker[White]}}], Mesh -> None],
ParametricPlot3D[{x3 + f[1 - z]*Cos[phi], y3 + f[1 - z]*Sin[phi],
z3 + z}, {z, 0, 1}, {phi, 0, 2*Pi},
PlotStyle ->
Directive[Specularity[RGBColor[1, 0.8, 0], 30], Lighter[Red],
Lighting -> {{"Directional", White, {1.5, 0, 3}}, {"Ambient",
Darker[White]}}], Mesh -> None],
ParametricPlot3D[{x2 + gx[1 - t], y2 + gy[1 - t],
z2 + gz[1 - t]}, {t, 0, 1},
PlotStyle -> Directive[Thickness[0.0075], Lighter[Black]]],
ParametricPlot3D[{x3 + gx[t], y3 + gy[1 - t], z3 + gz[1 - t]}, {t, 0,
1}, PlotStyle -> Directive[Thickness[0.0075], Lighter[Black]]],
PlotRange -> All]
The figure reminds of the ACM programming world team championship, the quarter finals of which take place in the fall. (At the finals of this championship, the team is given a ball for a correctly solved problem.)

Now I will give a few holiday drawings.
Here is a drawing made for the New Year. This is a Christmas tree built with the help of segments.
The code
a = 1;
b = 0.5;
c = 1.5;
h = 3.5;
dr[k_] := b + (c - b)/n*k;
dz[k_] := -(a - a/n*k);
z[k_] := h - h*k/n;
cnt = 0;
Do[Do[cnt = cnt + 1; phi = j*2*Pi/m + i*2*Pi/n;
ldx[cnt] = dr[i]*Cos[phi]; ldy[cnt] = dr[i]*Sin[phi];
ldz[cnt] = dz[i]; lz[cnt] = z[i], {j, 1, m}], {i, 1, n}]
ParametricPlot3D[
Table[{ldx[i]*t, ldy[i]*t, lz[i] + ldz[i]*t}, {i, 1, cnt}], {t, 0,
1}, PlotStyle -> Directive[Darker[Green], Thickness[0.005]]

This is a star made on February 23rd.
The code
gamma = Pi/10;
rho = 1;
p = rho*Sin[gamma];
k[phi_] := Floor[(phi + 0.2*Pi)/(0.4*Pi)];
s[phi_] := Sign[phi - 0.4*k[phi]*Pi];
alpha[phi_] := s[phi]*(Pi/2 - gamma) + 0.4*k[phi]*Pi;
PolarPlot[p/Cos[phi - Pi/2 - alpha[phi - Pi/2]], {phi, 0, 2*Pi},
PlotStyle -> Directive[Red, Thickness[0.01]]]

The asterisk is set using the polar equation of the line.
By the way, the parameter
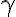 (half the angle of the star’s ray) can be varied. This star corresponds to the value
(half the angle of the star’s ray) can be varied. This star corresponds to the value 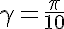 .
. When
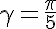 we get an asterisk similar to a starfish:
we get an asterisk similar to a starfish: 
When
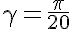 we get a spiky star:
we get a spiky star: 
Here is a picture that fits on Valentine's Day.
The code
f[x_, y_] := x^2 + (y - (x^2)^(1/3))^2 - 1;
h1[x_] := (x^2)^(1/3) + Sqrt[1 - x^2];
h2[x_] := (x^2)^(1/3) - Sqrt[1 - x^2];
Do[x0[i] = 1 - (i - 1)/6; y0[i] = h1[x0[i]]; k[i] = 4 + i, {i, 1, 6}];
x0[7] = 0; y0[7] = h1[x0[7]]; k[7] = 7;
xx0[1] = 0.95; yy0[1] = h2[xx0[1]];
kk[1] = 6; Do[xx0[i] = 1.1 - 0.15*i; yy0[i] = h2[xx0[i]];
kk[i] = 4 + i, {i, 2, 6}]
xx0[7] = 0; yy0[7] = h2[xx0[7]]; kk[7] = 6;
RegionPlot[
Or @@ Table[(f[(x - x0[i])*k[i], (y - y0[i])*k[i]] <=
0) || (f[(x + x0[i])*k[i], (y - y0[i])*k[i]] <= 0), {i, 1,
7}] ||
Or @@ Table[(f[(x - xx0[i])*kk[i], (y - yy0[i])*kk[i]] <=
0) || (f[(x + xx0[i])*kk[i], (y - yy0[i])*kk[i]] <= 0), {i, 1,
7}],
{x, -1.5, 1.5}, {y, -2.5, 2.5}, PlotStyle -> Red, AspectRatio -> 0.9,
PlotRange -> All, MaxRecursion -> 5]

You can even make a mathematical recognition:

And here is another mathematical heart. An autonomous system of 2 differential equations of the first order is considered. The phase portrait of this system is constructed (the trajectories of the system are drawn under various initial conditions) and the general integral of the system is found.
This system can be obtained by differentiating the general integral with respect to t. In this way (solving a system of differential equations), it is possible to construct graphs of equations.

And this is a mathematical card for March 8th. The figure shows a certain abstract computer, which built a graph of Bernoulli's lemniscata.

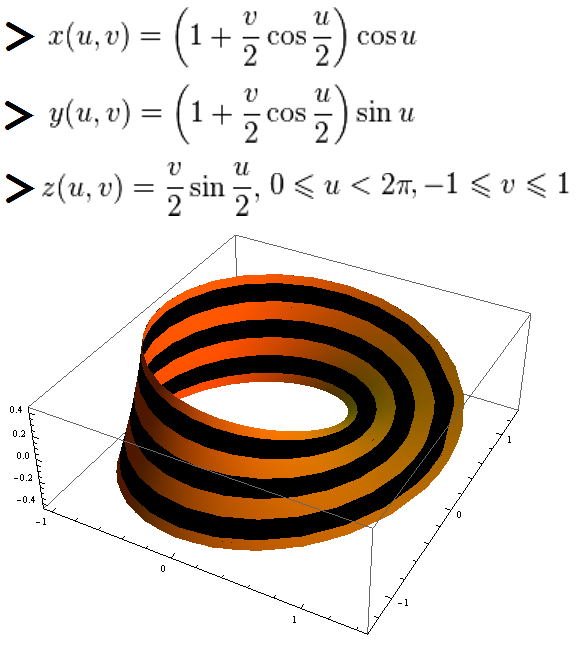
The figure shows the St. George Mobius strip by May 9th.
The code
f[i_, u_] :=
If[i == 0, -1 + 1/7 + u/7,
If[i == 6, -1 + 2*i/7 + u/7, -1 + 2*i/7 + u*2/7]];
ParametricPlot3D[
Evaluate@Table[{(1 + f[i, u]/2*Cos[phi/2])*
Cos[phi], (1 + f[i, u]/2*Cos[phi/2])*Sin[phi],
f[i, u]/2*Sin[phi/2]}, {i, 0, 6}], {u, 0, 1}, {phi, 0, 2*Pi},
Mesh -> None,
PlotStyle -> {Orange, Black, Orange, Black, Orange, Black, Orange}]

The following figure depicts a square academic cap, the figure is suitable for September 1.
The code
RegionPlot3D[((x^2 + y^2 + (z + 1.75)^2 <= 4 &&
x^2 + y^2 + (z + 1.75)^2 >= 4 - 1.4) || (z <= 0.1 &&
z >= 0)) && (z >= -1.5), {x, -2, 2}, {y, -2, 2}, {z, -2, 0.1},
BoxRatios -> {1, 1, 0.8}, PlotStyle -> Blue]

This figure shows the FEFU logo:

Here is the logo itself:

And this is the three-dimensional FEFU logo, which is also built using mathematical formulas in the Wolfram Mathematica package.
The code
g[z_] := 1/(1 + (1 - z)^2) - 1/2;
h[z_] := 1 - 1/2*Sqrt[1 + (z*Sqrt[3])^2];
f[z_] := If[z >= 0 && z <= 1, g[z], If[z >= 1 && z <= 2, h[z - 1]]]
phit[t_] := 2*Pi*t;
zt[t_] := 1.4*t;
zt1[t_] := 0.3 + 1.4*t;
zt2[t_] := 0.6 + 1.4*t;
phit1[t_] := 2*Pi*t;
phit2[t_] := 2*Pi*t;
k = 0.111;
ParametricPlot3D[{{f[zt[t] + k*s]*Cos[phit[t]],
f[zt[t] + k*s]*Sin[phit[t]],
zt[t] + k*s}, {f[zt1[t] + k*s]*Cos[phit1[t]],
f[zt1[t] + k*s]*Sin[phit1[t]],
zt1[t] + k*s}, {f[zt2[t] + k*s]*Cos[phit2[t]],
f[zt2[t] + k*s]*Sin[phit2[t]], zt2[t] + k*s}}, {t, 0, 1}, {s, -1,
1}, PlotStyle -> Blue, Mesh -> None, Axes -> False, Boxed -> False]

