Money, goods and some statistics
A couple of years ago I came across an interesting article on the relationship between gold and oil prices.
And I decided to expand the model a bit and conduct my own research.
First of all, to take not two goods, but a certain more substantial set.
After a long search on the Internet, I found this site from which I downloaded the price archive ( download XLS ) for products for 35 years.
I processed all the data in MATLAB.
As a relative price for more than two products, you can use the price divided by the geometric mean:
Charts of normalized prices:
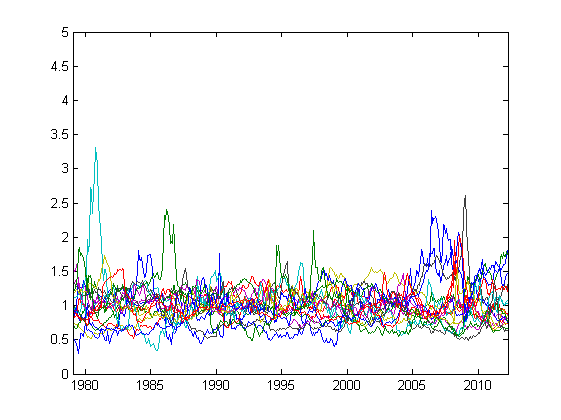
Standard deviations of relative prices as a percentage of the average over time:
Now try to make a diversified product (DP).
Let x be the vector of the relative quantity of goods, sum (x i ) = 1;
A - matrix of covariance of normalized prices.
Then the variance of the diversified product is calculated as X '* A * X;
We need to minimize it.
A typical conditional extremum problem is solved by the Lagrange multiplier method.
I will not go into details, it is decided as follows:
The composition of the DP is as follows:
We calculate the cost of DP:
Let's build the graphs:

Above is the graph of relative value, below is the value in dollars.
The standard deviation of the relative value of the DP for more than 30 years is only 1.06%!
But its value in dollars has increased (respectively, the purchasing power of the dollar has fallen).
So what can this purchasing power depend on?
Once upon a time I came across data on US government debt.
Here (p. 143-144), here I found detailed data on public debt and transferred it to the XLS file .
Get the data from the table:
And let’s try to build charts: The
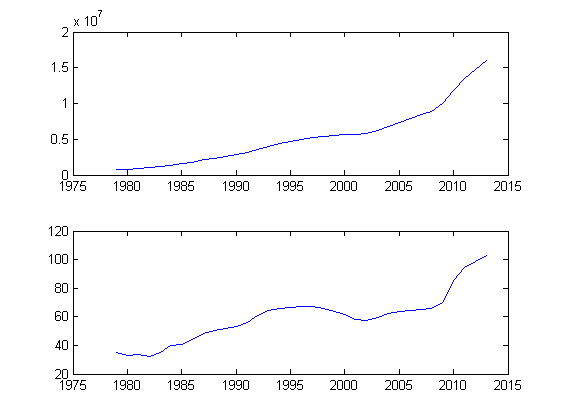
top chart is the volume of US government debt in millions of dollars, the bottom one as a percentage of GDP.
You may notice some similarities in the behavior of debt in% of GDP and the cost of a diversified product.
So why not try overlapping these two graphs?
To do this, smooth out the cost of the DP with a moving average, and interpolate the amount of debt for the entire time interval, as well as divide by the average over time:
We get the following picture:
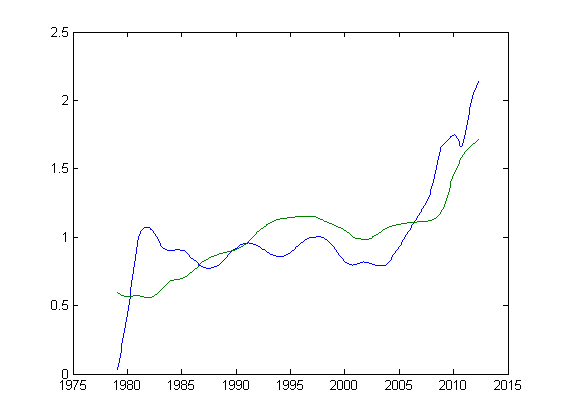
You can also calculate the correlation coefficient between the cost of subsidiaries in dollars and the amount of debt, it is 0.7165 or 71.65% - the figure is quite substantial.
The full matlab script can be viewed on github (link updated 6.09.2017).
How is the economy today?
As you know, most international transactions are made in US dollars.
The ruble is also pegged to the dollar - the Central Bank can issue exactly as many rubles to the economy as dollars received from exports, multiplying this amount by the dollar to ruble exchange rate.
What can be done?
Introduce the concept of a balanced monetary unit (SDE) and tie it not to some foreign currency, but to a diversified product.
This can be implemented as follows:
Suppose there is an SDE and the currency of a foreign country V.
The rate of the SDE in relation to V is indexed as the value of the DP in the currency V, multiplied by some coefficient q.
Consider the export and import operations.
Let's say 1V = 20 SDE.
Export.
Option 1.
An external buyer buys goods in the amount of 1000V or 20000SDE in the currency V.
1000V “settles” in the Central Bank, 20000SDE is issued to the economy.
Option 2.
An external buyer takes from the Central Bank 20000SDE and buys goods on them.
That is, in fact, undertakes in the future to return an equal amount of goods.
Import.
Option 1.
An internal buyer purchases goods from the outside in the amount of 1000V or 20,000 SDE in the currency V. The
Central Bank issues 1,000V from its reserves, and 20,000 SDE is removed from the economy.
Option 2. The
internal buyer purchases goods from outside in the SDE.
Conclusion: the introduction of an ETS in theory allows one to practically avoid inflation and introduce interest rates on loans close to zero.
And I decided to expand the model a bit and conduct my own research.
First of all, to take not two goods, but a certain more substantial set.
After a long search on the Internet, I found this site from which I downloaded the price archive ( download XLS ) for products for 35 years.
I processed all the data in MATLAB.
xls = xlsread('data.xls'); %загружаем данные из файла XLS
time = 1:399; %индекс
real_time = 1979 + time/12; %реальная дата
data = xls(time,1:22);
% получаем данные:
oil = data(:,1); % нефть
gold = data(:,2); % золото
iron = data(:,3); % железная руда
logs = data(:,4); % бревно
maize = data(:,5); % кукуруза
beef = data(:,6); % говядина
% и все остальные товары
% добавляем в матрицу те товары, которые будем подвергать анализу:
all_goods = [oil gold logs maize beef chicken gas tea tobacco wheat sugar soy rice cotton copper coffee coal];
goods_count = size(all_goods, 2); % количество товаров
As a relative price for more than two products, you can use the price divided by the geometric mean:
geom_average = ones(size(time))'; % для транспонирования в Матлабе используется символ '
%, но Хабр воспринимает его как начало строки
for i = 1:goods_count
geom_average = geom_average .* all_goods(:,i);
end
geom_average = geom_average .^ (1/goods_count); % среднее геометрическое
all_goods_rel = zeros(size(all_goods));
all_goods_norm = zeros(size(all_goods));
mean_ = zeros(1,goods_count);
std_ = zeros(1,goods_count);
percent_std_ = zeros(1,goods_count);
for i = 1:goods_count
all_goods_rel(:,i) = all_goods(:,i) ./ geom_average; % относительные цены товаров
mean_(i) = mean(all_goods_rel(:,i)); % среднее по времени
all_goods_norm(:,i) = all_goods_rel(:,i) / mean_(i); % относительные цены, нормированные на среднее по времени
std_(i) = std(all_goods_rel(:,i)); % стандартное отклонение по времени
percent_std_(i) = 100*std_(i)/mean_(i); % стандартное отклонение в процентах
end
Charts of normalized prices:

Standard deviations of relative prices as a percentage of the average over time:
| Raw oil | 37.77% | Gas | 32.18% | Rice | 19.71% |
| Gold | 21.57% | Tea | 25.18% | Cotton | 24.52% |
| Log | 20.33% | Tobacco | 20.55% | Copper | 36.24% |
| Corn | 15.71% | Wheat | 14.58% | Coffee | 37.08% |
| Beef | 19.39% | Sugar | 37.91% | Coal | 21.68% |
| Chicken meat | 25.47% | Soybean | 12.68% |
Now try to make a diversified product (DP).
Let x be the vector of the relative quantity of goods, sum (x i ) = 1;
A - matrix of covariance of normalized prices.
Then the variance of the diversified product is calculated as X '* A * X;
We need to minimize it.
A typical conditional extremum problem is solved by the Lagrange multiplier method.
I will not go into details, it is decided as follows:
A = cov(all_goods_rel); % матрица ковариаций
cond = ones(1, goods_count);
B = [2*A cond']; %'
B = [B; [cond 0]];
b = [zeros(1, goods_count) 1]';
x = (B^-1)*b;
The composition of the DP is as follows:
| Raw oil | 0.0035 barrels | Gas | 23.2 thousand BTU | Rice | 310.3 g |
| Gold | 9.627 mg | Tea | 76.3 g | Cotton | 98.1 g |
| Log | 0.353 cc dm | Tobacco | 45.69 g | Copper | 45.79 g |
| Corn | 970.2 g | Wheat | 514.2 g | Coffee | 40.7 g |
| Beef | 64.2 g | Sugar | 538.8 g | Coal | 3,5 kg |
| Chicken meat | 148.8 g | Soybean | 416.5 g |
We calculate the cost of DP:
DP = all_goods_rel*x(1:goods_count); % стоимость относительно среднего геометрического
USD_per_DP = all_goods*x(1:goods_count); % стоимость в долларах
Let's build the graphs:

Above is the graph of relative value, below is the value in dollars.
The standard deviation of the relative value of the DP for more than 30 years is only 1.06%!
But its value in dollars has increased (respectively, the purchasing power of the dollar has fallen).
So what can this purchasing power depend on?
Once upon a time I came across data on US government debt.
Get the data from the table:
debt_xls = xlsread('usa_debt.xls');
debt_time = debt_xls(:,1);
end_index = size(debt_time,1);
start_index = (1:end_index)*(debt_time == 1978);
debt_time = debt_time(start_index:end_index);
debt_usd = debt_xls(start_index:end_index,2);
debt_percent = debt_xls(start_index:end_index,3);
debt_time = debt_time + 1; % данные о долге даны на конец года, что равносильно началу следующего
And let’s try to build charts: The

top chart is the volume of US government debt in millions of dollars, the bottom one as a percentage of GDP.
You may notice some similarities in the behavior of debt in% of GDP and the cost of a diversified product.
So why not try overlapping these two graphs?
To do this, smooth out the cost of the DP with a moving average, and interpolate the amount of debt for the entire time interval, as well as divide by the average over time:
a = 1;
b = ones(1,24)/24;
debt_interp = interp1(debt_time, debt_percent, real_time, 'cubic')'; %'
USD_per_DP_mov_av = filter(b, a, USD_per_DP);
debt_and_DP = [USD_per_DP_mov_av/mean(USD_per_DP_mov_av) debt_interp/mean(debt_interp)];
debt_DP_corr = corr2(debt_and_DP(:,1),debt_and_DP(:,2))
figure;
plot(real_time, debt_and_DP);
We get the following picture:

You can also calculate the correlation coefficient between the cost of subsidiaries in dollars and the amount of debt, it is 0.7165 or 71.65% - the figure is quite substantial.
The full matlab script can be viewed on github (link updated 6.09.2017).
Afterword
How is the economy today?
As you know, most international transactions are made in US dollars.
The ruble is also pegged to the dollar - the Central Bank can issue exactly as many rubles to the economy as dollars received from exports, multiplying this amount by the dollar to ruble exchange rate.
What can be done?
Introduce the concept of a balanced monetary unit (SDE) and tie it not to some foreign currency, but to a diversified product.
This can be implemented as follows:
Suppose there is an SDE and the currency of a foreign country V.
The rate of the SDE in relation to V is indexed as the value of the DP in the currency V, multiplied by some coefficient q.
Consider the export and import operations.
Let's say 1V = 20 SDE.
Export.
Option 1.
An external buyer buys goods in the amount of 1000V or 20000SDE in the currency V.
1000V “settles” in the Central Bank, 20000SDE is issued to the economy.
Option 2.
An external buyer takes from the Central Bank 20000SDE and buys goods on them.
That is, in fact, undertakes in the future to return an equal amount of goods.
Import.
Option 1.
An internal buyer purchases goods from the outside in the amount of 1000V or 20,000 SDE in the currency V. The
Central Bank issues 1,000V from its reserves, and 20,000 SDE is removed from the economy.
Option 2. The
internal buyer purchases goods from outside in the SDE.
Conclusion: the introduction of an ETS in theory allows one to practically avoid inflation and introduce interest rates on loans close to zero.
