The probabilistic law of the distribution of the duration of a session of an artificial Earth satellite with a ground object
Part I of . Preliminary information about the system and model.
The design and calculation of the ballistic characteristics of satellite systems for various purposes, the modeling of the processes of motion and operation, require a preliminary assessment of the possibilities of achieving the planned target effects by such systems. The purpose is now reduced to information services in the broadest sense of target objects (CO) onboard equipment of an artificial Earth satellite (AES). Where information flows, there are always problems associated with its protection and ensuring information security, with all the ensuing consequences.
Long autonomous functioning leads to a change in the design values of ballistic characteristics, primarily the structure of satellite systems. In turn, this requires periodic correction of the values of part of the characteristics of the system. In this case, there is a need for their preliminary calculation, which is possible if measured values of the motion parameters are available, both for individual satellites of the systems and the system as a whole. Such measurements are possible if there is a network of ground-based measuring points (IP) stationary or mobile (land, sea, air) equipped with appropriate measuring equipment and command radio facilities. Here we consider a probabilistic approach to assessing and calculating the potential capabilities of satellite systems to influence information support in a global, planetary scale from the position of ballistic construction of the orbital part and the placement of objects, primarily measuring points, of the ground part. Information security issues are not considered.
An area of space (instantaneous service area (MLO)) is associated with each individual entrepreneur and central heating center. When an satellite enters this satellite, it can be serviced or perform central heating service itself. The service process includes, in addition to direct measurements of ballistic and telemetric characteristics, the reception and transmission of target information, communication with the satellite, the transfer of the correction program on board, the tabulation of the work program (RP) of the operation of on-board special equipment (BSpA), taking into account the updated movement parameters and other operations.
A priori, the process of obtaining the required estimates is impossible to implement deterministically, since the action of various natural and technogenic factors leads to perturbations of the parameters. First of all, the parameters of the satellite motion and, as a consequence, the characteristics of the functioning of the BSAA are subject to disturbances. Hence the need arises to study the named phenomena as random, to establish the probabilistic laws of the distribution of random events, quantities, functions of random arguments and random functions (fields).
In the work brought to the attention of readers, within the framework of the model of joint movement and functioning of the orbital and ground parts of the system, the interaction of a pair of AES - IP objects is considered. Moreover, the model includes all the main factors that shape the functioning process and generate the randomness of the onset of important system events. Of the many system events, the events of the interaction of the satellite with ground-based SPs and targets are distinguished.
Among the most important factors taken into account in the mathematical model of the system’s motion are:
- rotation of the planet around its axis (angular velocity constant);
- geographical location of the ground object (coordinates, radius of MLO);
- limited time of the interaction session (time spent by the object in the MLO);
- ballistic characteristics of the satellite (flight altitude H, inclination of the orbit plane).
In the mathematical model, simplifying assumptions and assumptions are used (introduced):
- the planet has a spherical shape with a radius of the sphere R, the gravitational field of attraction is central;
- the influence of the atmosphere on the movement of orbital objects is not taken into account;
- satellite orbits of motion - circular, the precession of the planes of the motion orbits is not taken into account;
- satellite motion paths are modeled by large circles of the sphere;
- MLO service areas — cones with a vertex in the center of the object, the intersection line of which with a sphere of radius R + H is projected onto the surface of the planet’s sphere with a flat circle.
The model of the satellite – IP interaction is based on the geometric model of system elements and the kinematic relations of their movement. In the three-dimensional space of the plane ор the orbits of each satellite of the system are motionless, their lines of intersection with the sphere of the planet are the paths. The MLO of a ground object (the projection onto the planet of the line of intersection of the cone with a sphere of radius R + H) is limited to the segment of the spherical surface cut off by the plane K. The MLO boundary is the circle L of a small circle, is “drawn” on the Earth’s surface and moves with the Earth. It periodically intersects with the orbital P plane of the satellite, i.e. the MLO segment is crossed by the route, which is also “drawn” on the Earth’s surface for each round of the satellite again. At some turns, the track crosses a segment, and at some it passes without going through it. Part of the track at the turn crossing the segment, from the entry point to the exit point lies inside the segment. The fact is that the passage of the path of one orbit by a satellite takes a time 15-16 times less than the length of the day, i.e. ≈ 1.5 hours. If the track crosses a segment, then the timeτ of the satellite’s stay in the MLO is proportional to the length t of the circle chord L, τ = t / 2πR.
Indeed, the antenna of the measuring instrument of the SP, turning, accompanies the moving satellite from the moment it enters the zone until it leaves it.
Substantive statement of the problem
The task is as follows. Determine the likelihood that the plane P of the satellite’s orbit will cut through the MLO segment at its random position relative to the MLO center.
For definiteness of the model and the convenience of reasoning, we introduce two coordinate systems: Cartesian and spherical (polar), the beginning of which is compatible with the center of a spherical planet. The position on the sphere of any point O1 in the spherical coordinate system will be determined by three coordinates:
- the length of the radius of the vector R;
- longitude λ;
- polar distance γо = π / 2 - φо.
The positive directions of the coordinate reference are shown in Fig. 1. The
axes oX, oy of the Cartesian coordinate system lie in the plane of the equator of the planet, the oX axis coincides with its intersection with the Greenwich meridian, the oy axis is rotated by λ = π / 2 and passes through the meridian with east longitude λ = π / 2, the oz axis complements the coordinate system to the right system. The formulas for the transition from spherical coordinates to Cartesian and vice versa have the form:
x = Rcosφoscosλо; y = Rcosφosininо; z is Rsinφo;
R = [x 2 + y 2 + z 2 ] o.5 ; λo = arctan y / x; φо = arctan z / √ (x 2 + y 2 ).
In the Cartesian coordinate system, the equation of the plane K forming a segment on the planetary sphere can be defined as
Ax + By + Cz + D = 0,
where A, B, C are the components of the vector n <3> normal to the plane K, D ≠ 0.
The direction cosines of the vector n <3> =perpendicular to the plane K, are determined by the formulas:
cos (α) = A / N; cos (β) = B / N; cos (γ) = C / N; N = [A 2 + B 2 + C 2 ] o.5 ; p = D / N,
where p is the distance from the origin to the plane, with sign (N) = –sign (D).
A characteristic of a segment having a circle L as the boundary, in addition to the position of its center, is the radius r of the circle L. This radius can be determined through the radius R of the sphere and the distance (p):
r = Rζc, where ζc = arccos (p / R).
Другими словами, сегмент на сфере может быть задан координатами точки О1(х, у,z) – центра сегмента и углом ζc, либо координатами точки О1(х, у,z) и расстоянием р, либо системой: уравнением сферы и уравнением плоскости К.
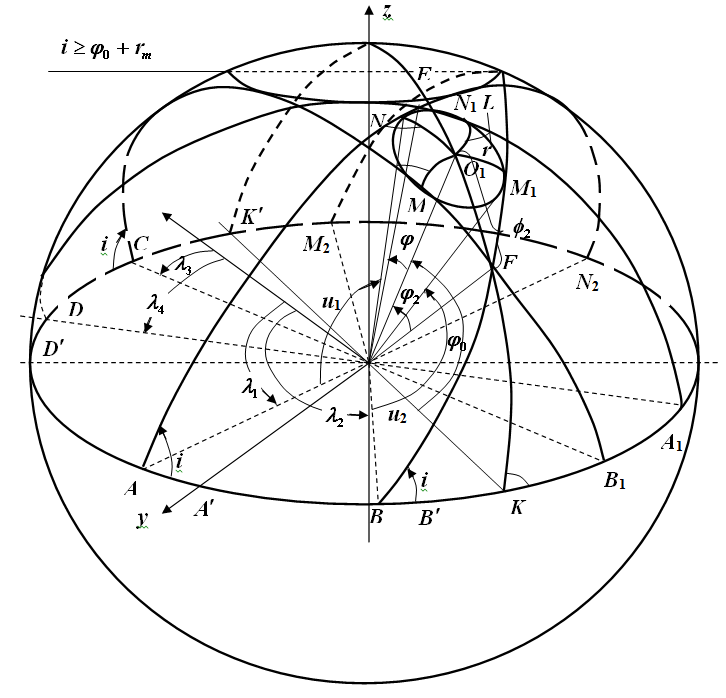
Рисунок 1 Положение трасс ИСЗ с углом наклона i большим широты верхней точки границы МЗО ИП
Плоскость П, проходящую через центр сферы, можно задать аналогичным образом, т. е. общим уравнением плоскости
А1х + B1y + C1z + D1 = 0.
Очевидно, для плоскости П значение D1 = 0. Существует более удобный для моделирования способ задания этой плоскости. В общем случае плоскость П наклонена к плоскости земного экватора, совпадающей с координатной горизонтальной хоу плоскостью, под некоторым углом i, called the inclination of the satellite orbital plane. The line of intersection of the planes of the orbit P and the horizontal coordinate hou plane is called the line of nodes (ascending and descending) of the orbit.
The position of this line in the equatorial plane is determined by the angle λ (geographic longitude), measured from the Greenwich meridian. At an arbitrary instant of time, the line of nodes of the orbit of some satellite is characterized by a random value of the angle λ. Obviously, the range of possible values of λ is determined by the interval λ ∊ [0, 2π]. At an arbitrary point in time within this interval, it is impossible to specify a point that would have a higher priority relative to all others being occupied by a satellite orbit node. There are no physical, mathematical, or any other justifications for this. Therefore, we assumethe probability distribution of a random value of longitude λ for the line of orbit nodes in the interval [0, 2π] is uniform .
The inclination angle i of the orbit plane to the equator plane will be considered nonrandom. In such a situation, it is more convenient for the plane P (i, λ) to use its representation through these angles, in the form:
x • tgλ - y + z • ctgi / cosλ = 0. For
each random position in the space of the orbit plane of the satellite A (i, λ) will correspond to one of the possible values of the random variable λ.
Passing by the satellite of the zone of the ground-based measuring point. The
practical interest for the designer of the satellite system consists in evaluating the possibility of conducting a communication session between an artificial satellite and a satellite at each turn of the trajectory.
We denote by ℬ the random complex event consisting in the fact that, for a random value of longitude λ, the plane П (i, λ) passing through the center of the planet’s sphere intersects a segment bounded by a circle L centered on the radius vector of the point О1 (x, у , z). Thus, in this part of the work, the task is to determine the probability of the occurrence of a random event ℬ. The probability determination will be carried out under the condition that λ takes one of its possible values. It is clear that the imposed condition is always satisfied. The methods of probability theory allow you to determine the probabilities of some events (complex) through the known probabilities of other events, in a certain way associated with them, and the probabilities of which are given or can be determined in one way or another.
Let us analyze the possibilities of implementing event ℬ. Figure 1 illustrates the geometry of various situations with previously considered objects that favor the occurrence of a simulated random event ℬ and shows the conditions for the impossibility of its occurrence.
Figure 1 shows the upper hemisphere of the planet and arcs of large and small circles are drawn on it. The closed curve MNN1M1 represents the boundary of the MLO segment (circle L). The position of the center of the segment O1 (x, y, z) is characterized by a latitudinal angle φo and a longitudinal angle λo. The position of the plane P (i, λ) is determined by the angle of inclination i to the plane of the equator, which is determined and does not change during the simulation.
Analysis of possible situations for a random event ℬ.
We will distinguish between situations that lead to different functional dependencies that generate a complex random event ℬ:
The first situation is φо + r m ≤ i. There are four positions of the arcs of the large circles ANN2, BM1M2, CMB1, DN1A1 formed by the section of the sphere by the plane П (i, λ) for four values of λ corresponding to such positions of the plane at which it touches the boundary of the segment (circle L) at four points N, M1 , N1, M. The arc KO1K1 is formed by a section of the sphere by a plane perpendicular to the plane of the ho in the meridian section and passing through the z axis and the point O1.
In a section of the planet’s sphere, the equatorial plane of the hou shows the lines of the nodes of the planes mentioned above.
Angles are also shown:
- u1, u2 - between the lines of nodes and directions to the points of tangency of the circle L, measured by arcs AN and BM1, respectively;
- φ1, φ2 - between the radius vector of the center of the segment and the directions to the intersection points of large circles, measured by arcs O1E and O1F in the meridian section;
- i - the angle of inclination of the plane P (i, λ) to the plane of the how.

Figure 2 The position of the satellite tracks with an inclination angle i less than the latitude of the upper point of the boundary of the MLO IP
The second situation is φo - r m ≤ i ≤ φo + r m . The following figure 2 below shows two positions of the plane П (i, λ) for two values of λ corresponding to its tangency to the circle L at points M and M1.
Based on the analysis of the figures, it can be concluded that the realization of the random event ℬ will correspond to the nodal point of the plane П (i, λ) in two intervals AB and CD of the equatorial circle in upper Figure 1 and in one interval of CB in lower Figure 2.
Top the figure corresponds to the interval of variation of the inclination angle i of the plane
φо + ζc ≤ i ≤ π - φо - ζc, to the
lower figure - φо - ζc ≤ i ≤ φо + ζc.
We call the intervals AB and CD (in the lower figure CB) the intervals when the plane P (i, λ) hits the segment or, in short, the intervals. For each fixed position and size ζc of the segment and the angle i of inclination of the plane П (i, λ), there are uniquely determined hit intervals. The positions, sizes, number of hit intervals depend on the angle i, the coordinates of the center of the segment (φо, λо) and the radius ζc of the segment.
It follows from the analysis that the random event is complex and can be represented through random simple events, consisting in the fact that the random value λ will belong to the intervals AB and CD for the situation in the upper figure and the interval CB for the situation in the lower figure.
The third situation φo - r m> i. This situation is not considered in the work, since it does not correspond to the occurrence of a random event ℬ. The satellite motion plane is inclined so low above the equator that the MLO of the objects cannot intersect with it.
Representation of a complex random event ℬ simple random events .
We introduce the notation ℬ1 = (λ∊ ﺭ AB) and ℬ2 = (λ∊ ﺭ CD), then ℬ = ℬ1 + ℬ2. Events ℬ1 and ℬ2 are incompatible and, therefore, provided that the distribution law of the longitude of the node λ is known, the relation P (ℬ) = P (ℬ1) + (ℬ2) will be satisfied.
Let the probability distribution of a random variable λ over a large circle in the plane of hou, i.e. in the interval [0, 2 π ], is given by some continuous function of the longitude of the node — the probability density function
φ λ(λ) = dF λ (λ) / dλ, where F λ (λ) is the distribution function of λ.
If two arcs are marked on the numerical axis λ by the boundary points A, B and C, D, then the probability of getting λ on the intervals of the arcs AB and CD is described as

P (ℬ1) = ∫φ λ (λ) dλ; P (ℬ2) = ∫φ λ (λ) dλ is determined by the integrals in these indicated limits; therefore,
P (ℬ) = ∫φ λ (λ) dλ + ∫φ λ(λ) dλ, where the values of the integration limits have not yet been determined. Thus, to determine the probabilities P (ℬ), it is necessary to obtain expressions for the boundaries of the intervals characterized by the lengths of the arcs λj, j = 1 (1) 4. It was previously noted that λj = λj (R, φо, λо, i, ζc), j = 1 (1) 4. We find explicitly expressions for the lengths of the hit intervals.
We turn to the analysis of Figure 1. From its consideration, we can write (we use the notation for the arc ﺭ DD):
λ1 = λА = λо - ﺭ АК; λ2 = λВ = λо - ﺭ VK; λ3 = λС = λо - π + ﺭ VK; λ4 = λD = λо - π + ﺭ AK.
Relations for performing numerical calculations We
use the theorems of spherical trigonometry and obtain calculation formulas for the necessary variables.
Here arcs are determined from the right-angled spherical triangles AEK and BFK:
cs AK = arcsin (tg (φо + φ1) / tgi); ﺭ BK = arcsin (tg (φо - φ2) / tgi).
The unknown quantities φ2, φ1, λj = λj (R, φо, λо, i, ζc), j = 1 (1) 4 will be determined through the known φо, i, ζc.
From the spherical triangle NEO1, by the sine theorem, we can write the relation
sin ζc / sind = sin φ1 / sin90 °, where the angle d = ے NEO1, from the relation we obtain sind = sin ζc / sin φ1.
By the cosine theorem from the spherical triangle AEK, we write the relation
cosi = sindcos (φо + φ1), from which for sind we obtain another dependence sind = cosi / cos (φо + φ1).
Equate the two dependencies found in different ways and perform the transformation (we transfer functions with the variable φ1 to the left)
sin ζc / sin φ1 = cosi / cos (φо + φ1) or cos (φо + φ1) / sin φ1 = cosi / sin ζc.
In the last expression, unknown is the only variable φ1, which was able to be coupled through known quantities, which allows us to transform it and make it convenient to calculate
cos (φо + φ1) / sin φ1 = cos φоctg φ1 - sin φо and then cos φоctg φ1 - sin φo = cosi / sin ζc, whence ctg
φ1 = (cosi / sin ζc + sinφo) / cosφo and finally,
φ1 = arctg (cos φo sin ζc / (cosi + sinφosin ζc)).
By analogy, considering the spherical triangles OMF and BFK, we obtain the value
φ2 = arctan (cos φo sin ζc / (cosi - sinφosin ζc)).
Substituting the obtained values of φ1 and φ2 into the relations for longitude λj, j = 1 (1) 4, we can write
λ1 = λА = λо - arcsin (tg (φо + arctg (cos φо sin ζc / (cosi + sinφosin ζc))) / tgi);
λ2 = λB = λо - arcsin (tg (φо - arctg (cos φо sin ζc / (cosi - sinφоsin ζc))) / tgi);
λ3 = λC = λо - π + arcsin (tg (φо - arctg (cos φо sin ζc / (cosi - sinφоsin ζc))) / tgi);
λ4 = λD = λо - π + arcsin (tg (φо + arctg (cos φо sin ζc / (cosi + sinφоsin ζc))) / tgi).
Thus, all the necessary data for calculating the probability P (ℬ) are defined.
Consider an example . In applications, it is assumed that the law of distribution of longitude λj is uniform in the interval [0, 2π]. Under this assumption, the distribution function F λ(λ) and distribution density φ λ (λ) of the random variable λ are written in the form shown under Figure 3: The
numerical characteristics of these distribution laws are determined from the expressions: mathematical expectation m (λ) = π; standard deviation sigma (λ) = π / √3; dispersion D (λ) = π 2 /3. For this case, the probability of a satellite entering the service area of an IP is written in the form (taking into account the corresponding integration and summation limits)
P (ℬ) = ∫φ λ (λ) dλ + ∫φ λ (λ) dλ = 1 / 2π ∑ | λ 2j - λ 2j – 1 |, j = 1,2.
Substituting the values of the found integration limits and the found expressions λj into the last relation, we obtain the final expression for the probability of the satellite entering the zone of the measuring point
P (ℬ) = 1 / π ∑ (-1) k arcsin (tg (φо - (- 1) k arctg (cos φo sin ζc / (cosi - (- 1) k sinφosin ζc))) / tgi), k = 1,2.
This ratio allows us to move from the fact that the satellite passed through the service area of a ground station to the solution of the problem of determining the time of a satellite’s stay in the zone of a station, depending on the numerical characteristics of the system’s movement (the position of the longitude of the ascending node of the orbit at the turn of falling into the IP zone). This part of the work by the author is planned for publication in the near future.
The design and calculation of the ballistic characteristics of satellite systems for various purposes, the modeling of the processes of motion and operation, require a preliminary assessment of the possibilities of achieving the planned target effects by such systems. The purpose is now reduced to information services in the broadest sense of target objects (CO) onboard equipment of an artificial Earth satellite (AES). Where information flows, there are always problems associated with its protection and ensuring information security, with all the ensuing consequences.
Long autonomous functioning leads to a change in the design values of ballistic characteristics, primarily the structure of satellite systems. In turn, this requires periodic correction of the values of part of the characteristics of the system. In this case, there is a need for their preliminary calculation, which is possible if measured values of the motion parameters are available, both for individual satellites of the systems and the system as a whole. Such measurements are possible if there is a network of ground-based measuring points (IP) stationary or mobile (land, sea, air) equipped with appropriate measuring equipment and command radio facilities. Here we consider a probabilistic approach to assessing and calculating the potential capabilities of satellite systems to influence information support in a global, planetary scale from the position of ballistic construction of the orbital part and the placement of objects, primarily measuring points, of the ground part. Information security issues are not considered.
An area of space (instantaneous service area (MLO)) is associated with each individual entrepreneur and central heating center. When an satellite enters this satellite, it can be serviced or perform central heating service itself. The service process includes, in addition to direct measurements of ballistic and telemetric characteristics, the reception and transmission of target information, communication with the satellite, the transfer of the correction program on board, the tabulation of the work program (RP) of the operation of on-board special equipment (BSpA), taking into account the updated movement parameters and other operations.
A priori, the process of obtaining the required estimates is impossible to implement deterministically, since the action of various natural and technogenic factors leads to perturbations of the parameters. First of all, the parameters of the satellite motion and, as a consequence, the characteristics of the functioning of the BSAA are subject to disturbances. Hence the need arises to study the named phenomena as random, to establish the probabilistic laws of the distribution of random events, quantities, functions of random arguments and random functions (fields).
In the work brought to the attention of readers, within the framework of the model of joint movement and functioning of the orbital and ground parts of the system, the interaction of a pair of AES - IP objects is considered. Moreover, the model includes all the main factors that shape the functioning process and generate the randomness of the onset of important system events. Of the many system events, the events of the interaction of the satellite with ground-based SPs and targets are distinguished.
Among the most important factors taken into account in the mathematical model of the system’s motion are:
- rotation of the planet around its axis (angular velocity constant);
- geographical location of the ground object (coordinates, radius of MLO);
- limited time of the interaction session (time spent by the object in the MLO);
- ballistic characteristics of the satellite (flight altitude H, inclination of the orbit plane).
In the mathematical model, simplifying assumptions and assumptions are used (introduced):
- the planet has a spherical shape with a radius of the sphere R, the gravitational field of attraction is central;
- the influence of the atmosphere on the movement of orbital objects is not taken into account;
- satellite orbits of motion - circular, the precession of the planes of the motion orbits is not taken into account;
- satellite motion paths are modeled by large circles of the sphere;
- MLO service areas — cones with a vertex in the center of the object, the intersection line of which with a sphere of radius R + H is projected onto the surface of the planet’s sphere with a flat circle.
The model of the satellite – IP interaction is based on the geometric model of system elements and the kinematic relations of their movement. In the three-dimensional space of the plane ор the orbits of each satellite of the system are motionless, their lines of intersection with the sphere of the planet are the paths. The MLO of a ground object (the projection onto the planet of the line of intersection of the cone with a sphere of radius R + H) is limited to the segment of the spherical surface cut off by the plane K. The MLO boundary is the circle L of a small circle, is “drawn” on the Earth’s surface and moves with the Earth. It periodically intersects with the orbital P plane of the satellite, i.e. the MLO segment is crossed by the route, which is also “drawn” on the Earth’s surface for each round of the satellite again. At some turns, the track crosses a segment, and at some it passes without going through it. Part of the track at the turn crossing the segment, from the entry point to the exit point lies inside the segment. The fact is that the passage of the path of one orbit by a satellite takes a time 15-16 times less than the length of the day, i.e. ≈ 1.5 hours. If the track crosses a segment, then the timeτ of the satellite’s stay in the MLO is proportional to the length t of the circle chord L, τ = t / 2πR.
Indeed, the antenna of the measuring instrument of the SP, turning, accompanies the moving satellite from the moment it enters the zone until it leaves it.
Substantive statement of the problem
The task is as follows. Determine the likelihood that the plane P of the satellite’s orbit will cut through the MLO segment at its random position relative to the MLO center.
For definiteness of the model and the convenience of reasoning, we introduce two coordinate systems: Cartesian and spherical (polar), the beginning of which is compatible with the center of a spherical planet. The position on the sphere of any point O1 in the spherical coordinate system will be determined by three coordinates:
- the length of the radius of the vector R;
- longitude λ;
- polar distance γо = π / 2 - φо.
The positive directions of the coordinate reference are shown in Fig. 1. The
axes oX, oy of the Cartesian coordinate system lie in the plane of the equator of the planet, the oX axis coincides with its intersection with the Greenwich meridian, the oy axis is rotated by λ = π / 2 and passes through the meridian with east longitude λ = π / 2, the oz axis complements the coordinate system to the right system. The formulas for the transition from spherical coordinates to Cartesian and vice versa have the form:
x = Rcosφoscosλо; y = Rcosφosininо; z is Rsinφo;
R = [x 2 + y 2 + z 2 ] o.5 ; λo = arctan y / x; φо = arctan z / √ (x 2 + y 2 ).
In the Cartesian coordinate system, the equation of the plane K forming a segment on the planetary sphere can be defined as
Ax + By + Cz + D = 0,
where A, B, C are the components of the vector n <3> normal to the plane K, D ≠ 0.
The direction cosines of the vector n <3> =
cos (α) = A / N; cos (β) = B / N; cos (γ) = C / N; N = [A 2 + B 2 + C 2 ] o.5 ; p = D / N,
where p is the distance from the origin to the plane, with sign (N) = –sign (D).
A characteristic of a segment having a circle L as the boundary, in addition to the position of its center, is the radius r of the circle L. This radius can be determined through the radius R of the sphere and the distance (p):
r = Rζc, where ζc = arccos (p / R).
Другими словами, сегмент на сфере может быть задан координатами точки О1(х, у,z) – центра сегмента и углом ζc, либо координатами точки О1(х, у,z) и расстоянием р, либо системой: уравнением сферы и уравнением плоскости К.

Рисунок 1 Положение трасс ИСЗ с углом наклона i большим широты верхней точки границы МЗО ИП
Плоскость П, проходящую через центр сферы, можно задать аналогичным образом, т. е. общим уравнением плоскости
А1х + B1y + C1z + D1 = 0.
Очевидно, для плоскости П значение D1 = 0. Существует более удобный для моделирования способ задания этой плоскости. В общем случае плоскость П наклонена к плоскости земного экватора, совпадающей с координатной горизонтальной хоу плоскостью, под некоторым углом i, called the inclination of the satellite orbital plane. The line of intersection of the planes of the orbit P and the horizontal coordinate hou plane is called the line of nodes (ascending and descending) of the orbit.
The position of this line in the equatorial plane is determined by the angle λ (geographic longitude), measured from the Greenwich meridian. At an arbitrary instant of time, the line of nodes of the orbit of some satellite is characterized by a random value of the angle λ. Obviously, the range of possible values of λ is determined by the interval λ ∊ [0, 2π]. At an arbitrary point in time within this interval, it is impossible to specify a point that would have a higher priority relative to all others being occupied by a satellite orbit node. There are no physical, mathematical, or any other justifications for this. Therefore, we assumethe probability distribution of a random value of longitude λ for the line of orbit nodes in the interval [0, 2π] is uniform .
The inclination angle i of the orbit plane to the equator plane will be considered nonrandom. In such a situation, it is more convenient for the plane P (i, λ) to use its representation through these angles, in the form:
x • tgλ - y + z • ctgi / cosλ = 0. For
each random position in the space of the orbit plane of the satellite A (i, λ) will correspond to one of the possible values of the random variable λ.
Passing by the satellite of the zone of the ground-based measuring point. The
practical interest for the designer of the satellite system consists in evaluating the possibility of conducting a communication session between an artificial satellite and a satellite at each turn of the trajectory.
We denote by ℬ the random complex event consisting in the fact that, for a random value of longitude λ, the plane П (i, λ) passing through the center of the planet’s sphere intersects a segment bounded by a circle L centered on the radius vector of the point О1 (x, у , z). Thus, in this part of the work, the task is to determine the probability of the occurrence of a random event ℬ. The probability determination will be carried out under the condition that λ takes one of its possible values. It is clear that the imposed condition is always satisfied. The methods of probability theory allow you to determine the probabilities of some events (complex) through the known probabilities of other events, in a certain way associated with them, and the probabilities of which are given or can be determined in one way or another.
Let us analyze the possibilities of implementing event ℬ. Figure 1 illustrates the geometry of various situations with previously considered objects that favor the occurrence of a simulated random event ℬ and shows the conditions for the impossibility of its occurrence.
Figure 1 shows the upper hemisphere of the planet and arcs of large and small circles are drawn on it. The closed curve MNN1M1 represents the boundary of the MLO segment (circle L). The position of the center of the segment O1 (x, y, z) is characterized by a latitudinal angle φo and a longitudinal angle λo. The position of the plane P (i, λ) is determined by the angle of inclination i to the plane of the equator, which is determined and does not change during the simulation.
Analysis of possible situations for a random event ℬ.
We will distinguish between situations that lead to different functional dependencies that generate a complex random event ℬ:
The first situation is φо + r m ≤ i. There are four positions of the arcs of the large circles ANN2, BM1M2, CMB1, DN1A1 formed by the section of the sphere by the plane П (i, λ) for four values of λ corresponding to such positions of the plane at which it touches the boundary of the segment (circle L) at four points N, M1 , N1, M. The arc KO1K1 is formed by a section of the sphere by a plane perpendicular to the plane of the ho in the meridian section and passing through the z axis and the point O1.
In a section of the planet’s sphere, the equatorial plane of the hou shows the lines of the nodes of the planes mentioned above.
Angles are also shown:
- u1, u2 - between the lines of nodes and directions to the points of tangency of the circle L, measured by arcs AN and BM1, respectively;
- φ1, φ2 - between the radius vector of the center of the segment and the directions to the intersection points of large circles, measured by arcs O1E and O1F in the meridian section;
- i - the angle of inclination of the plane P (i, λ) to the plane of the how.

Figure 2 The position of the satellite tracks with an inclination angle i less than the latitude of the upper point of the boundary of the MLO IP
The second situation is φo - r m ≤ i ≤ φo + r m . The following figure 2 below shows two positions of the plane П (i, λ) for two values of λ corresponding to its tangency to the circle L at points M and M1.
Based on the analysis of the figures, it can be concluded that the realization of the random event ℬ will correspond to the nodal point of the plane П (i, λ) in two intervals AB and CD of the equatorial circle in upper Figure 1 and in one interval of CB in lower Figure 2.
Top the figure corresponds to the interval of variation of the inclination angle i of the plane
φо + ζc ≤ i ≤ π - φо - ζc, to the
lower figure - φо - ζc ≤ i ≤ φо + ζc.
We call the intervals AB and CD (in the lower figure CB) the intervals when the plane P (i, λ) hits the segment or, in short, the intervals. For each fixed position and size ζc of the segment and the angle i of inclination of the plane П (i, λ), there are uniquely determined hit intervals. The positions, sizes, number of hit intervals depend on the angle i, the coordinates of the center of the segment (φо, λо) and the radius ζc of the segment.
It follows from the analysis that the random event is complex and can be represented through random simple events, consisting in the fact that the random value λ will belong to the intervals AB and CD for the situation in the upper figure and the interval CB for the situation in the lower figure.
The third situation φo - r m> i. This situation is not considered in the work, since it does not correspond to the occurrence of a random event ℬ. The satellite motion plane is inclined so low above the equator that the MLO of the objects cannot intersect with it.
Representation of a complex random event ℬ simple random events .
We introduce the notation ℬ1 = (λ∊ ﺭ AB) and ℬ2 = (λ∊ ﺭ CD), then ℬ = ℬ1 + ℬ2. Events ℬ1 and ℬ2 are incompatible and, therefore, provided that the distribution law of the longitude of the node λ is known, the relation P (ℬ) = P (ℬ1) + (ℬ2) will be satisfied.
Let the probability distribution of a random variable λ over a large circle in the plane of hou, i.e. in the interval [0, 2 π ], is given by some continuous function of the longitude of the node — the probability density function
φ λ(λ) = dF λ (λ) / dλ, where F λ (λ) is the distribution function of λ.
If two arcs are marked on the numerical axis λ by the boundary points A, B and C, D, then the probability of getting λ on the intervals of the arcs AB and CD is described as

P (ℬ1) = ∫φ λ (λ) dλ; P (ℬ2) = ∫φ λ (λ) dλ is determined by the integrals in these indicated limits; therefore,
P (ℬ) = ∫φ λ (λ) dλ + ∫φ λ(λ) dλ, where the values of the integration limits have not yet been determined. Thus, to determine the probabilities P (ℬ), it is necessary to obtain expressions for the boundaries of the intervals characterized by the lengths of the arcs λj, j = 1 (1) 4. It was previously noted that λj = λj (R, φо, λо, i, ζc), j = 1 (1) 4. We find explicitly expressions for the lengths of the hit intervals.
We turn to the analysis of Figure 1. From its consideration, we can write (we use the notation for the arc ﺭ DD):
λ1 = λА = λо - ﺭ АК; λ2 = λВ = λо - ﺭ VK; λ3 = λС = λо - π + ﺭ VK; λ4 = λD = λо - π + ﺭ AK.
Relations for performing numerical calculations We
use the theorems of spherical trigonometry and obtain calculation formulas for the necessary variables.
Here arcs are determined from the right-angled spherical triangles AEK and BFK:
cs AK = arcsin (tg (φо + φ1) / tgi); ﺭ BK = arcsin (tg (φо - φ2) / tgi).
The unknown quantities φ2, φ1, λj = λj (R, φо, λо, i, ζc), j = 1 (1) 4 will be determined through the known φо, i, ζc.
From the spherical triangle NEO1, by the sine theorem, we can write the relation
sin ζc / sind = sin φ1 / sin90 °, where the angle d = ے NEO1, from the relation we obtain sind = sin ζc / sin φ1.
By the cosine theorem from the spherical triangle AEK, we write the relation
cosi = sindcos (φо + φ1), from which for sind we obtain another dependence sind = cosi / cos (φо + φ1).
Equate the two dependencies found in different ways and perform the transformation (we transfer functions with the variable φ1 to the left)
sin ζc / sin φ1 = cosi / cos (φо + φ1) or cos (φо + φ1) / sin φ1 = cosi / sin ζc.
In the last expression, unknown is the only variable φ1, which was able to be coupled through known quantities, which allows us to transform it and make it convenient to calculate
cos (φо + φ1) / sin φ1 = cos φоctg φ1 - sin φо and then cos φоctg φ1 - sin φo = cosi / sin ζc, whence ctg
φ1 = (cosi / sin ζc + sinφo) / cosφo and finally,
φ1 = arctg (cos φo sin ζc / (cosi + sinφosin ζc)).
By analogy, considering the spherical triangles OMF and BFK, we obtain the value
φ2 = arctan (cos φo sin ζc / (cosi - sinφosin ζc)).
Substituting the obtained values of φ1 and φ2 into the relations for longitude λj, j = 1 (1) 4, we can write
λ1 = λА = λо - arcsin (tg (φо + arctg (cos φо sin ζc / (cosi + sinφosin ζc))) / tgi);
λ2 = λB = λо - arcsin (tg (φо - arctg (cos φо sin ζc / (cosi - sinφоsin ζc))) / tgi);
λ3 = λC = λо - π + arcsin (tg (φо - arctg (cos φо sin ζc / (cosi - sinφоsin ζc))) / tgi);
λ4 = λD = λо - π + arcsin (tg (φо + arctg (cos φо sin ζc / (cosi + sinφоsin ζc))) / tgi).
Thus, all the necessary data for calculating the probability P (ℬ) are defined.
Consider an example . In applications, it is assumed that the law of distribution of longitude λj is uniform in the interval [0, 2π]. Under this assumption, the distribution function F λ(λ) and distribution density φ λ (λ) of the random variable λ are written in the form shown under Figure 3: The
numerical characteristics of these distribution laws are determined from the expressions: mathematical expectation m (λ) = π; standard deviation sigma (λ) = π / √3; dispersion D (λ) = π 2 /3. For this case, the probability of a satellite entering the service area of an IP is written in the form (taking into account the corresponding integration and summation limits)
P (ℬ) = ∫φ λ (λ) dλ + ∫φ λ (λ) dλ = 1 / 2π ∑ | λ 2j - λ 2j – 1 |, j = 1,2.
Substituting the values of the found integration limits and the found expressions λj into the last relation, we obtain the final expression for the probability of the satellite entering the zone of the measuring point
P (ℬ) = 1 / π ∑ (-1) k arcsin (tg (φо - (- 1) k arctg (cos φo sin ζc / (cosi - (- 1) k sinφosin ζc))) / tgi), k = 1,2.
This ratio allows us to move from the fact that the satellite passed through the service area of a ground station to the solution of the problem of determining the time of a satellite’s stay in the zone of a station, depending on the numerical characteristics of the system’s movement (the position of the longitude of the ascending node of the orbit at the turn of falling into the IP zone). This part of the work by the author is planned for publication in the near future.
