Automatic optimization of algorithms by quickly raising matrices to a power
Suppose we want to calculate the ten millionth Fibonacci number by a Python program. A function using a trivial algorithm on my computer will perform calculations for more than 25 minutes. But if you apply a special optimizing decorator to the function, the function will calculate the answer in just 18 seconds ( 85 times faster ):

The fact is that before running the program, the Python interpreter compiles all its parts into a special byte code. Using the method described habrapolzovatelem SkidanovAlex , the decorator analyzes the resulting byte-code function, and tries to optimize the algorithm is applied there. Further you will see that this optimization can accelerate the program not a certain number of times, but asymptotically. So, the greater the number of iterations in the loop, the more times the optimized function will accelerate compared to the original one.
This article will talk about when and how the decorator manages to do such optimizations. You can also download and test the cpmoptimize library containing this decorator yourself .
Two years ago, SkidanovAlex published an interesting article describing a limited language interpreter that supports the following operations:
The values of variables in the language must be numbers, their size is not limited ( long arithmetic is supported ). In fact, variables are stored as integers in Python, which switches to long arithmetic mode if the number goes beyond the boundaries of a hardware-supported four- or eight-byte type.
Consider the case when long arithmetic is not used. Then the execution time of operations will not depend on the values of the variables, which means that in the loop all iterations will be performed in the same time. If you execute such code “forehead”, as in conventional interpreters, the cycle will be executed in time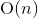 , where n is the number of iterations. In other words, if the code for n iterations works for time t , then the code for
, where n is the number of iterations. In other words, if the code for n iterations works for time t , then the code for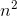 iterations will work over time
iterations will work over time 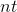 (see computational complexity ).
(see computational complexity ).
The interpreter from the original article presents each language-supported operation with variables in the form of a certain matrix by which the vector with the original values of the variables is multiplied. As a result of multiplication, we get a vector with new values of the variables:
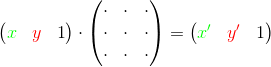
Thus, in order to perform a sequence of operations, we must take turns multiplying the vector by a matrix corresponding to the next operation. Another way - using associativity, you can first multiply matrices by each other, and then multiply the original vector by the resulting product:

To execute the loop, we must calculate the number n- the number of iterations in the cycle, as well as the matrix B - a sequential product of matrices corresponding to operations from the body of the cycle. Then you need to multiply the original vector by the matrix B n times . Another way is to first raise the matrix B to the power of n , and then multiply the vector with the variables by the result: If you use the binary raising to the power algorithm , the cycle can be completed in much less time . So, if the code for n iterations works in time t , then the code for iterations will work in time (only twice as slow, and not in n
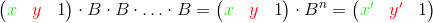
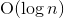
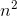
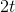 times slower, as in the previous case).
times slower, as in the previous case).
As a result, as was written above, the greater the number of iterations in the cycle n , the more times the optimized function accelerates. Therefore, the effect of optimization will be especially noticeable for large n .
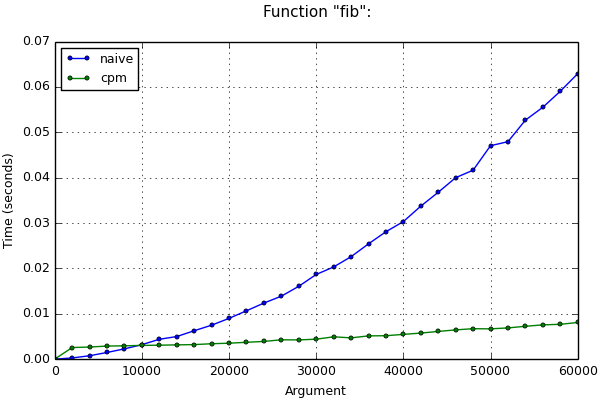
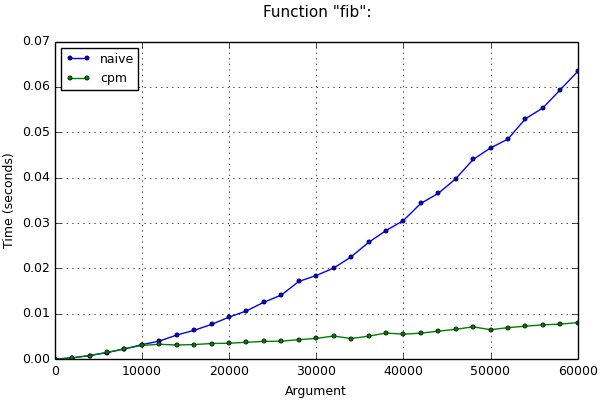
If long arithmetic is still used, time estimates above may not be correct. For example, when computing nof the Fibonacci number, the values of variables from iteration to iteration become more and more, and operations with them slow down. In this case, it is more difficult to make an asymptotic estimate of the program run time (it is necessary to take into account the length of numbers in variables at each iteration and the methods used for multiplying numbers) and it will not be given here. Nevertheless, after applying this optimization method, the asymptotic behavior improves even in this case. This is clearly visible on the chart:
Если десятки лет назад программисту потребовалось бы умножить переменную в программе на 4, он использовал бы не операцию умножения, а её более быстрый эквивалент — битовый сдвиг влево на 2. Теперь компиляторы сами умеют делать подобные оптимизации. В борьбе за сокращение времени разработки появились языки с высоким уровнем абстракции, новые удобные технологии и библиотеки. При написании программ всё большую часть своего времени разработчики тратят на объяснение компьютеру того, что должна сделать программа (умножить число на 4), а не того, как ей это сделать эффективно (использовать битовый сдвиг). Таким образом, задача создания эффективного кода частично переносится на компиляторы и интерпретаторы.
Now compilers are able to replace various operations with more efficient ones, predict the values of expressions, delete or interchange parts of code. But compilers have not yet replaced the calculation algorithm written by man with an asymptotically more efficient one.
The implementation of the described method, presented in the original article, is problematic to use in real programs, since for this you will have to rewrite part of the code in a special language, and to interact with this code you will have to run a third-party script with an interpreter. However, the author of the article suggests using his best practices in practice in optimizing compilers. I tried to implement this method for optimizing Python programs in a form that is really suitable for use in real projects.
If you use the library that I wrote, to apply the optimization it will be enough to append before the function that you need to speed up, one line using a special decorator. This decorator independently optimizes the cycles, if possible, and under no circumstances “breaks” the program.
Consider a number of tasks in which our decorator can come in handy.
Suppose we have some sequence corresponding to the rule depicted in the diagram, and we need to calculate its nth term:
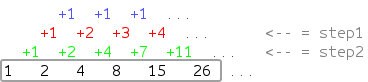
In this case, it is intuitively clear how the next member of the sequence appears, but it takes time to come up with and prove a mathematical formula corresponding to it. Nevertheless, we can write a trivial algorithm that describes our rule, and suggest that the computer itself figure out how to quickly read the answer to our problem:
Interestingly, if you run this function for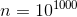 , inside it will start a loop with
, inside it will start a loop with 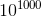 iterations. Without optimization, such a function would not have finished working for any conceivable period of time, but with the decorator it takes less than a second, while returning the correct result.
iterations. Without optimization, such a function would not have finished working for any conceivable period of time, but with the decorator it takes less than a second, while returning the correct result.
To quickly calculate the nth Fibonacci number, there is a fast but non-trivial algorithm based on the same idea of raising matrices to a power. An experienced developer can implement it in a few minutes. If the code where such calculations are performed does not need to work quickly (for example, if you need to calculate the Fibonacci number with a number less than 10 thousand once), to save his working time, the developer will most likely decide to save his efforts and write a solution “in forehead".
If the program still needs to work quickly, either you have to make an effort and write a complex algorithm, or you can use the automatic optimization method by applying our decorator to the function. If nlarge enough, in both cases the productivity of the programs will be almost the same, but in the second case, the developer will spend less than his working time.
You can compare the runtimes of the methods described below in the tables and graphs for small and large n .
In fairness, it should be noted that there is another algorithm known as fast doubling for calculating Fibonacci numbers . He wins the previous algorithms somewhat in time, since unnecessary additions and multiplications of numbers are excluded in it. The calculation time through this algorithm is also presented in the graphs for comparison.
In practice, we may encounter a more complicated situation if the sequence of numbers instead of the well-known recurrence formula
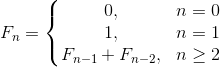
is given by a somewhat complicated formula, for example, this:

In this case, we will not be able to find the implementation of the above algorithms on the Internet, but to manually invent an algorithm with the construction matrices to a power, it will take a substantial amount of time. Nevertheless, we can write the solution “forehead” and apply the decorator, then the computer will come up with a quick algorithm for us:
Suppose we need to calculate the sum of count members of a geometric progression, for which the first member start and the denominator coeff are given . In this task, the decorator is again able to optimize our trivial solution:
Suppose we need to raise the number a to a non-negative integer power n . In such a task, the decorator will actually replace the trivial solution with a binary exponentiation algorithm :
You can install the library using pip :
The source code for the library with examples is available on github under the free MIT license.
UPD. The package is published in the Python Package Index.
Examples of optimization are in the " tests / " folder . Each example consists of a function that represents a “head-on” solution, its optimized version, and also functions that represent well-known complex, but quick solutions to a given problem. These functions are placed in scripts that run them on various groups of tests, measure the time of their work and build the corresponding tables. If the matplotlib library is installed , the scripts will also build graphs of the dependence of the operating time of the functions on the input data (regular or logarithmic) and save them in the "tests / plots / ".
When creating the library, I took advantage of the fact that the byte code of the program that the Python interpreter creates can be analyzed and changed at runtime without interfering with the interpreter, which gives ample opportunity to expand the language (see, for example, the implementation of goto construction ). The advantages of the described method are usually manifested when using long arithmetic, which is also built into Python.
For these reasons, implementing the described optimization in Python has become a more interesting task for me, although, of course, its use in C ++ compilers would allow the creation of even faster programs. In addition, decorator-optimized Python code tends to overtake C ++ code forehead due to its better asymptotic behavior.
When modifying the bytecode, I used the byteplay module , which provides a convenient interface for disassembling and assembling bytecode. Unfortunately, the module has not yet been ported to Python 3, so I implemented the entire project in Python 2.7.
The name of the cpmoptimize library is short for " c ompute the p ower of a m atrix and optimize " . The volume of the article does not allow us to describe in detail the process of analysis and modification of bytecode, however I will try to describe in detail what features this library provides and on what principles its work is based.
cpmoptimize. xrange ( stop )
cpmoptimize. xrange ( start , stop [, step ]) The
built-in xrange type in Python 2 does not support long integers of the long type as arguments for optimization purposes :
Since when using our library, loops with the number of order operations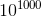 can be completed in less than a second, and become commonplace in the program, the library provides its own implementation of the xrange type in pure Python (inside the library it is called CPMRange ). It supports all the features of regular xrange and, in addition, arguments of type long . Such code will not lead to errors and quickly calculate the correct result:
can be completed in less than a second, and become commonplace in the program, the library provides its own implementation of the xrange type in pure Python (inside the library it is called CPMRange ). It supports all the features of regular xrange and, in addition, arguments of type long . Such code will not lead to errors and quickly calculate the correct result:
Nevertheless, if in your case the number of iterations in the cycles is small, you can continue to use the built-in xrange with the decorator .
cpmoptimize. cpmoptimize ( strict = False, iters_limit = 5000, types = (int, long), opt_min_rows = True, opt_clear_stack = True)
The cpmoptimize function accepts the parameters of the optimization performed and returns a decorator that takes these parameters into account, which should be applied to the optimized function. This can be done using special syntax (with or without the “dog” symbol):
Before making changes to the bytecode, the original function is copied. Thus, in the code above, the functions f and smart_g will eventually be optimized, while naive_g will not.
The decorator looks for standard for loops in the bytecode of the function , while while loops and for loops inside the generator and list expressions are ignored. Nested loops are not yet supported (only the innermost loop is optimized). For-else constructions are correctly processed .
The decorator cannot optimize the loop no matter what types of variables are used in it. The fact is that, for example, Python allows you to determine the type that, with each multiplication, writes a string to a file. As a result of applying the optimization, the number of multiplications made in the function could change. Because of this, the number of lines in the file would be different and optimization would break the program.
In addition, when operations with matrices, variables are added and multiplied implicitly, so the types of variables can be “mixed up”. If one of the constants or variables would be of type float , those variables that should have been of type int after execution of the code could also be of type float (since adding intand float returns float ). Such behavior can cause errors in the program and is also unacceptable.
To avoid unwanted side effects, the decorator optimizes the loop only if all the constants and variables used in it are of a valid type. The initial valid types are int and long , as well as types inherited from them. If one of the constants or variables is of type long , those variables that should have been of type int after execution of the code can also be of type long . However, since int and longin Python are interchangeable enough, this should not lead to errors.
In case you want to change the set of valid types (for example, to add support for float ), you must pass a tuple of the required types in the types parameter . Types that are part of this tuple or inherited from types that are part of this tuple will be considered valid. In fact, checking that any value has a valid type will be performed using the expression isinstance (value, types) .
Each cycle found must satisfy a number of conditions. Some of them are checked already when using the decorator:
If these conditions are met, a “trap” is set before the cycle, which will check another part of the conditions, while the original byte code of the cycle is not deleted. Since Python uses dynamic typing, the following conditions can only be checked immediately before starting the loop:
If the “trap” concluded that the optimization is acceptable, the necessary matrices will be calculated, and then the values of the variables used will be changed to new ones. If optimization cannot be performed, the original bytecode of the loop will be launched.
Despite the fact that the described method does not support exponentiation and bitwise AND operations, the following code will be optimized:
When analyzing the bytecode, the decorator concludes that the values of the variables k and m in the expression (k ** m) & 676 do not depend on which iteration of the cycle they are used, and therefore the value of the entire expression does not change. It is not necessary to calculate it at each iteration; it is enough to calculate this value once. Therefore, the corresponding bytecode instructions can be taken out and executed immediately before the start of the cycle, substituting the ready-made value in the cycle. The code will be converted to the following:
This technique is known as the removal of the invariant code per cycle ( loop-invariant below code motion ). Please note that the values removed are calculated each time the function starts, as they may depend on changing global variables or function parameters (as _const1 in the example depends on the parameter k ). The resulting code is now easily optimized using matrices.
It is at this stage that the above predictability check is performed. For example, if one of the operands of the bitwise AND were unpredictable, this operation could no longer be taken out of the loop and optimization could not be applied.
The decorator also partially supports multiple assignments. If there are few elements in them, Python creates bytecode supported by the decorator without using tuples:
In the graphs above, you may have noticed that with a small number of iterations, the optimized cycle can work slower than usual, since in this case it still takes some time to construct the matrices and type check. In cases where it is necessary for the function to work as fast as possible and with a small number of iterations, you can explicitly set the threshold with the iters_limit parameter . Then the “trap” before starting the optimization will check how many iterations the loop has to complete and cancel the optimization if this number does not exceed the specified threshold.
Initially, the threshold is set to 5000 iterations. It cannot be set lower than in 2 iterations.
It is clear that the most favorable threshold value is the intersection point on the graph of lines corresponding to the operating time of the optimized and initial versions of the function. If the threshold is set exactly this way, the function will be able to choose the fastest algorithm in this case (optimized or initial):
In some cases, optimization should be mandatory. So, if in a loop of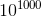 iterations, without optimization, the program simply freezes. In this case, the strict parameter is provided . Initially, its value is False , but if it is set to True , an exception will be thrown if one of the standard for loops has not been optimized.
iterations, without optimization, the program simply freezes. In this case, the strict parameter is provided . Initially, its value is False , but if it is set to True , an exception will be thrown if one of the standard for loops has not been optimized.
If the fact that optimization is not applicable was detected at the stage of applying the decorator, an exception cpmoptimize.recompiler.RecompilationError will be immediately raised . In the example in the loop, two unpredictable variables are multiplied:
If that optimization is not applicable was detected before the loop execution (that is, if it turned out that the types of iterator values or variables are not supported), a TypeError exception will be thrown :
Two flags opt_min_rows and opt_clear_stack are responsible for the use of additional optimization methods when constructing matrices. Initially, they are turned on, the ability to turn them off is present only for demonstration purposes (thanks to it, you can compare the effectiveness of these methods).
When executing optimized code, the majority of the time is occupied by the multiplication of long numbers in some cells of the generated matrices. Compared to this time-consuming process, the time spent on multiplying all other cells is negligible.
In the process of recompiling expressions, the decorator creates intermediate, virtualvariables responsible for the position of the interpreter stack. After complex calculations, they may leave long numbers that are already stored in some other, real variables. We no longer need to store these values a second time, however, they remain in the cells of the matrix and significantly slow down the program, since when we multiply the matrices, we are forced to multiply these long numbers once again. The opt_clear_stack option is responsible for clearing such variables: if you assign them zero at the end of their use, long values disappear in them.
This option is especially effective when the program operates with very large numbers. The elimination of unnecessary multiplications of such numbers allows you to speed up the program more than twice. Opt_min_rows
optioninvolves minimizing the size of the square matrices that we multiply. Rows corresponding to unused and predictable variables are excluded from matrices. If the loop variable itself is not used, the rows responsible for maintaining its correct value are also excluded. In order not to disrupt the program, after the cycle, all these variables will be assigned the correct final values. In addition, in the original article, the vector of variables was supplemented by an element equal to unity. If the row corresponding to this element is unused, it will also be excluded.
This option can slightly speed up the program for not very large n , when the numbers have not yet become very long and the dimensions of the matrix make a significant contribution to the running time of the program.
If you use both options at the same time, then the virtual variables begin to have a predictable (zero) value, and opt_min_rows works even more efficiently. In other words, the effectiveness of both options together is greater than the effectiveness of each of them individually.
The graph below shows the operating time of the program for calculating Fibonacci numbers when disabling certain options (here "-m" is the program with opt_min_rows disabled , "-c" is the program with opt_clear_stack disabled , "-mc" is the program where both options are disabled immediately ):

We will say that our method supports a couple of operations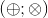 if:
if:
We already know that the method supports a couple of operations . Really:
. Really:
It is these operations that are currently implemented in the optimizing decorator. However, it turns out that the described method supports other pairs of operations, including (a pair of multiplication and exponentiation).
(a pair of multiplication and exponentiation).
For example, our task may be to find the nth number in the sequence specified by the recurrence relation:
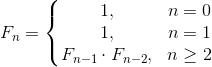
If our decorator supported a couple of operations , we could multiply the variable by another variable (but could not add the variables anymore). In this case, the following trivial solution to this problem could be accelerated by the decorator:
, we could multiply the variable by another variable (but could not add the variables anymore). In this case, the following trivial solution to this problem could be accelerated by the decorator:
We can prove that our method also supports pairs of operations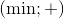 ,
,  and
and 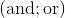 (here and is a bitwise AND, or is a bitwise OR). In the case of positive numbers, you can work with pairs of operations
(here and is a bitwise AND, or is a bitwise OR). In the case of positive numbers, you can work with pairs of operations 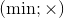 and
and 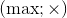 .
.
To implement support for operations , for example, one can operate not with the values of variables, but with the logarithms of these values. Then the multiplication of variables will be replaced by the addition of logarithms, and the raising of a variable to a constant power will be replaced by the multiplication of the logarithm by a constant. Thus, we reduce the problem to the already realized case with operations
, for example, one can operate not with the values of variables, but with the logarithms of these values. Then the multiplication of variables will be replaced by the addition of logarithms, and the raising of a variable to a constant power will be replaced by the multiplication of the logarithm by a constant. Thus, we reduce the problem to the already realized case with operations  .
.
The explanation of how to implement support for the remaining specified pairs of operations contains a certain number of mathematical calculations and is worthy of a separate article. At the moment, it is only worth mentioning that the pairs of operations are to some extent interchangeable.
By refining the loop analysis algorithm in bytecode, you can implement support for nested loops to optimize code like this:
In the following code, the condition in the loop body is predictable. Before starting the cycle, you can find out if it is true and remove the non-executing code branch. The resulting code can be optimized:
The Python interpreter, generally speaking, produces predictable bytecode that almost exactly matches the source code you wrote. By default, it does not perform any inlining of functions, nor unfolding of loops, nor any other optimizations that require analysis of program behavior. Only since version 2.6 did CPython learn to collapse constant arithmetic expressions, but this feature does not always work efficiently.
There are several reasons for this situation. Firstly, the analysis of code in the general case in Python is difficult, because data types can only be tracked during program execution (which we do in our case). Secondly, optimizations, as a rule, still do not allow Python to achieve the speed of purely compiled languages, therefore, in the case when the program needs to work very quickly, it is proposed to simply write it in a lower level language.
However, Python is a flexible language that allows you to implement many optimization methods yourself if necessary without interfering with the interpreter. This library, as well as other projects listed below, illustrate this opportunity well.
UPD. The project description is now also available as a presentation on SlideShare.
Below I will provide links to several other interesting projects to speed up the execution of programs in Python:
UPD # 1. User magik suggested a few links:
UPD # 2. A DuneRat user pointed to several other Python compilation projects: shedskin , hope , pythran .

The fact is that before running the program, the Python interpreter compiles all its parts into a special byte code. Using the method described habrapolzovatelem SkidanovAlex , the decorator analyzes the resulting byte-code function, and tries to optimize the algorithm is applied there. Further you will see that this optimization can accelerate the program not a certain number of times, but asymptotically. So, the greater the number of iterations in the loop, the more times the optimized function will accelerate compared to the original one.
This article will talk about when and how the decorator manages to do such optimizations. You can also download and test the cpmoptimize library containing this decorator yourself .
Theory
Two years ago, SkidanovAlex published an interesting article describing a limited language interpreter that supports the following operations:
# Присвоить переменной другую переменную или константу
x = y
x = 1
# Сложить или вычесть из переменной другую переменную или константу
x += y
x += 2
x -= y
x -= 3
# Умножить переменную на константу
x *= 4
# Запустить цикл с константным числом итераций
loop 100000
...
end
The values of variables in the language must be numbers, their size is not limited ( long arithmetic is supported ). In fact, variables are stored as integers in Python, which switches to long arithmetic mode if the number goes beyond the boundaries of a hardware-supported four- or eight-byte type.
Consider the case when long arithmetic is not used. Then the execution time of operations will not depend on the values of the variables, which means that in the loop all iterations will be performed in the same time. If you execute such code “forehead”, as in conventional interpreters, the cycle will be executed in time
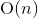 , where n is the number of iterations. In other words, if the code for n iterations works for time t , then the code for
, where n is the number of iterations. In other words, if the code for n iterations works for time t , then the code for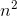 iterations will work over time
iterations will work over time 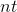 (see computational complexity ).
(see computational complexity ). The interpreter from the original article presents each language-supported operation with variables in the form of a certain matrix by which the vector with the original values of the variables is multiplied. As a result of multiplication, we get a vector with new values of the variables:

Thus, in order to perform a sequence of operations, we must take turns multiplying the vector by a matrix corresponding to the next operation. Another way - using associativity, you can first multiply matrices by each other, and then multiply the original vector by the resulting product:

To execute the loop, we must calculate the number n- the number of iterations in the cycle, as well as the matrix B - a sequential product of matrices corresponding to operations from the body of the cycle. Then you need to multiply the original vector by the matrix B n times . Another way is to first raise the matrix B to the power of n , and then multiply the vector with the variables by the result: If you use the binary raising to the power algorithm , the cycle can be completed in much less time . So, if the code for n iterations works in time t , then the code for iterations will work in time (only twice as slow, and not in n
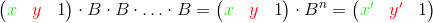
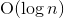
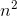
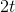 times slower, as in the previous case).
times slower, as in the previous case). As a result, as was written above, the greater the number of iterations in the cycle n , the more times the optimized function accelerates. Therefore, the effect of optimization will be especially noticeable for large n .
If long arithmetic is still used, time estimates above may not be correct. For example, when computing nof the Fibonacci number, the values of variables from iteration to iteration become more and more, and operations with them slow down. In this case, it is more difficult to make an asymptotic estimate of the program run time (it is necessary to take into account the length of numbers in variables at each iteration and the methods used for multiplying numbers) and it will not be given here. Nevertheless, after applying this optimization method, the asymptotic behavior improves even in this case. This is clearly visible on the chart:

Idea
Если десятки лет назад программисту потребовалось бы умножить переменную в программе на 4, он использовал бы не операцию умножения, а её более быстрый эквивалент — битовый сдвиг влево на 2. Теперь компиляторы сами умеют делать подобные оптимизации. В борьбе за сокращение времени разработки появились языки с высоким уровнем абстракции, новые удобные технологии и библиотеки. При написании программ всё большую часть своего времени разработчики тратят на объяснение компьютеру того, что должна сделать программа (умножить число на 4), а не того, как ей это сделать эффективно (использовать битовый сдвиг). Таким образом, задача создания эффективного кода частично переносится на компиляторы и интерпретаторы.
Now compilers are able to replace various operations with more efficient ones, predict the values of expressions, delete or interchange parts of code. But compilers have not yet replaced the calculation algorithm written by man with an asymptotically more efficient one.
The implementation of the described method, presented in the original article, is problematic to use in real programs, since for this you will have to rewrite part of the code in a special language, and to interact with this code you will have to run a third-party script with an interpreter. However, the author of the article suggests using his best practices in practice in optimizing compilers. I tried to implement this method for optimizing Python programs in a form that is really suitable for use in real projects.
If you use the library that I wrote, to apply the optimization it will be enough to append before the function that you need to speed up, one line using a special decorator. This decorator independently optimizes the cycles, if possible, and under no circumstances “breaks” the program.
Examples of using
Consider a number of tasks in which our decorator can come in handy.
Example No. 1. Long cycles
Suppose we have some sequence corresponding to the rule depicted in the diagram, and we need to calculate its nth term:

In this case, it is intuitively clear how the next member of the sequence appears, but it takes time to come up with and prove a mathematical formula corresponding to it. Nevertheless, we can write a trivial algorithm that describes our rule, and suggest that the computer itself figure out how to quickly read the answer to our problem:
from cpmoptimize import cpmoptimize, xrange
@cpmoptimize()
def f(n):
step1 = 1
step2 = 1
res = 1
for i in xrange(n):
res += step2
step2 += step1
step1 += 1
return res
Interestingly, if you run this function for
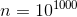 , inside it will start a loop with
, inside it will start a loop with 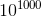 iterations. Without optimization, such a function would not have finished working for any conceivable period of time, but with the decorator it takes less than a second, while returning the correct result.
iterations. Without optimization, such a function would not have finished working for any conceivable period of time, but with the decorator it takes less than a second, while returning the correct result.Example No. 2. Fibonacci numbers
To quickly calculate the nth Fibonacci number, there is a fast but non-trivial algorithm based on the same idea of raising matrices to a power. An experienced developer can implement it in a few minutes. If the code where such calculations are performed does not need to work quickly (for example, if you need to calculate the Fibonacci number with a number less than 10 thousand once), to save his working time, the developer will most likely decide to save his efforts and write a solution “in forehead".
If the program still needs to work quickly, either you have to make an effort and write a complex algorithm, or you can use the automatic optimization method by applying our decorator to the function. If nlarge enough, in both cases the productivity of the programs will be almost the same, but in the second case, the developer will spend less than his working time.
You can compare the runtimes of the methods described below in the tables and graphs for small and large n .
In fairness, it should be noted that there is another algorithm known as fast doubling for calculating Fibonacci numbers . He wins the previous algorithms somewhat in time, since unnecessary additions and multiplications of numbers are excluded in it. The calculation time through this algorithm is also presented in the graphs for comparison.
Graphs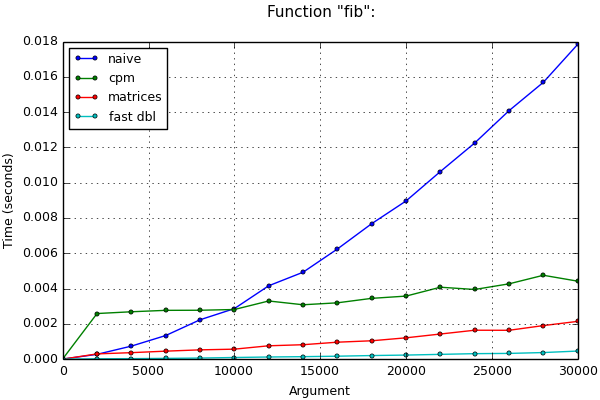
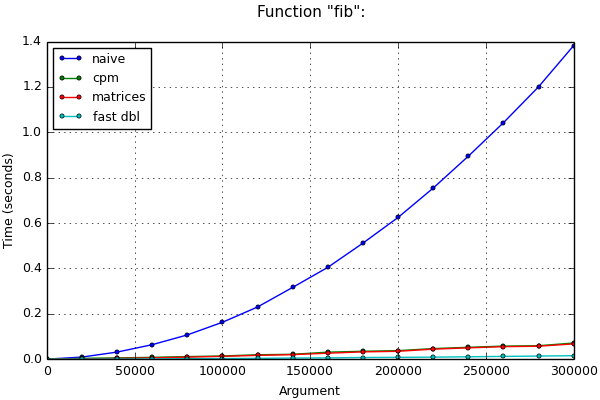


Time Results
Function "fib":
(*) Testcase "big":
+--------+----------+--------------+--------------+--------------+-------+
| arg | naive, s | cpm, s | matrices, s | fast dbl, s | match |
+--------+----------+--------------+--------------+--------------+-------+
| 0 | 0.00 | 0.00 | 0.00 | 0.00 | True |
| 20000 | 0.01 | 0.00 (2.5x) | 0.00 (3.0x) | 0.00 (5.1x) | True |
| 40000 | 0.03 | 0.01 (5.7x) | 0.00 (1.8x) | 0.00 (4.8x) | True |
| 60000 | 0.06 | 0.01 (7.9x) | 0.01 (1.4x) | 0.00 (4.8x) | True |
| 80000 | 0.11 | 0.01 (9.4x) | 0.01 (1.3x) | 0.00 (4.6x) | True |
| 100000 | 0.16 | 0.01 (11.6x) | 0.01 (1.1x) | 0.00 (4.5x) | True |
| 120000 | 0.23 | 0.02 (11.8x) | 0.02 (1.2x) | 0.00 (4.7x) | True |
| 140000 | 0.32 | 0.02 (14.7x) | 0.02 (1.1x) | 0.00 (4.1x) | True |
| 160000 | 0.40 | 0.03 (13.1x) | 0.03 (1.2x) | 0.01 (4.6x) | True |
| 180000 | 0.51 | 0.03 (14.7x) | 0.03 (1.1x) | 0.01 (4.4x) | True |
| 200000 | 0.62 | 0.04 (16.6x) | 0.03 (1.1x) | 0.01 (4.4x) | True |
| 220000 | 0.75 | 0.05 (16.1x) | 0.04 (1.1x) | 0.01 (4.9x) | True |
| 240000 | 0.89 | 0.05 (17.1x) | 0.05 (1.0x) | 0.01 (4.7x) | True |
| 260000 | 1.04 | 0.06 (18.1x) | 0.06 (1.0x) | 0.01 (4.5x) | True |
| 280000 | 1.20 | 0.06 (20.2x) | 0.06 (1.0x) | 0.01 (4.2x) | True |
| 300000 | 1.38 | 0.07 (19.4x) | 0.07 (1.1x) | 0.02 (4.4x) | True |
+--------+----------+--------------+--------------+--------------+-------+
In practice, we may encounter a more complicated situation if the sequence of numbers instead of the well-known recurrence formula
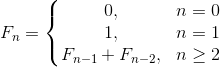
is given by a somewhat complicated formula, for example, this:

In this case, we will not be able to find the implementation of the above algorithms on the Internet, but to manually invent an algorithm with the construction matrices to a power, it will take a substantial amount of time. Nevertheless, we can write the solution “forehead” and apply the decorator, then the computer will come up with a quick algorithm for us:
from cpmoptimize import cpmoptimize
@cpmoptimize()
def f(n):
prev3 = 0
prev2 = 1
prev1 = 1
for i in xrange(3, n + 3):
cur = 7 * (2 * prev1 + 3 * prev2) + 4 * prev3 + 5 * i + 6
prev3, prev2, prev1 = prev2, prev1, cur
return prev3
Example No. 3. Sum of geometric progression
Suppose we need to calculate the sum of count members of a geometric progression, for which the first member start and the denominator coeff are given . In this task, the decorator is again able to optimize our trivial solution:
from cpmoptimize import cpmoptimize
@cpmoptimize()
def geom_sum(start, coeff, count):
res = 0
elem = start
for i in xrange(count):
res += elem
elem *= coeff
return res
Schedule

Example No. 4. Exponentiation
Suppose we need to raise the number a to a non-negative integer power n . In such a task, the decorator will actually replace the trivial solution with a binary exponentiation algorithm :
from cpmoptimize import cpmoptimize
@cpmoptimize()
def power(a, n):
res = 1
for i in xrange(n):
res *= a
return res
Schedule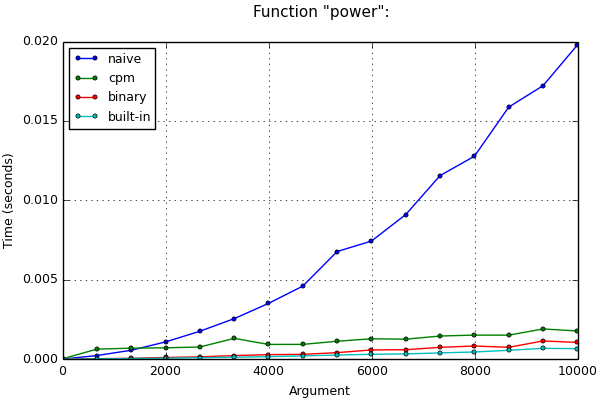

Download links
You can install the library using pip :
sudo pip install cpmoptimizeThe source code for the library with examples is available on github under the free MIT license.
UPD. The package is published in the Python Package Index.
Examples of optimization are in the " tests / " folder . Each example consists of a function that represents a “head-on” solution, its optimized version, and also functions that represent well-known complex, but quick solutions to a given problem. These functions are placed in scripts that run them on various groups of tests, measure the time of their work and build the corresponding tables. If the matplotlib library is installed , the scripts will also build graphs of the dependence of the operating time of the functions on the input data (regular or logarithmic) and save them in the "tests / plots / ".
Library description
When creating the library, I took advantage of the fact that the byte code of the program that the Python interpreter creates can be analyzed and changed at runtime without interfering with the interpreter, which gives ample opportunity to expand the language (see, for example, the implementation of goto construction ). The advantages of the described method are usually manifested when using long arithmetic, which is also built into Python.
For these reasons, implementing the described optimization in Python has become a more interesting task for me, although, of course, its use in C ++ compilers would allow the creation of even faster programs. In addition, decorator-optimized Python code tends to overtake C ++ code forehead due to its better asymptotic behavior.
When modifying the bytecode, I used the byteplay module , which provides a convenient interface for disassembling and assembling bytecode. Unfortunately, the module has not yet been ported to Python 3, so I implemented the entire project in Python 2.7.
The name of the cpmoptimize library is short for " c ompute the p ower of a m atrix and optimize " . The volume of the article does not allow us to describe in detail the process of analysis and modification of bytecode, however I will try to describe in detail what features this library provides and on what principles its work is based.
Own xrange
cpmoptimize. xrange ( stop )
cpmoptimize. xrange ( start , stop [, step ]) The
built-in xrange type in Python 2 does not support long integers of the long type as arguments for optimization purposes :
>>> xrange(10 ** 1000)
Traceback (most recent call last):
File "", line 1, in
OverflowError: Python int too large to convert to C long
Since when using our library, loops with the number of order operations
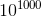 can be completed in less than a second, and become commonplace in the program, the library provides its own implementation of the xrange type in pure Python (inside the library it is called CPMRange ). It supports all the features of regular xrange and, in addition, arguments of type long . Such code will not lead to errors and quickly calculate the correct result:
can be completed in less than a second, and become commonplace in the program, the library provides its own implementation of the xrange type in pure Python (inside the library it is called CPMRange ). It supports all the features of regular xrange and, in addition, arguments of type long . Such code will not lead to errors and quickly calculate the correct result:from cpmoptimize import cpmoptimize, xrange
@cpmoptimize()
def f():
res = 0
for i in xrange(10 ** 1000):
res += 3
return res
print f()
Nevertheless, if in your case the number of iterations in the cycles is small, you can continue to use the built-in xrange with the decorator .
Cpmoptimize function
cpmoptimize. cpmoptimize ( strict = False, iters_limit = 5000, types = (int, long), opt_min_rows = True, opt_clear_stack = True)
Decorator application
The cpmoptimize function accepts the parameters of the optimization performed and returns a decorator that takes these parameters into account, which should be applied to the optimized function. This can be done using special syntax (with or without the “dog” symbol):
from cpmoptimize import cpmoptimize
@cpmoptimize()
def f(n):
# Некоторый код
def naive_g(n):
# Некоторый код
smart_g = cpmoptimize()(naive_g)
Before making changes to the bytecode, the original function is copied. Thus, in the code above, the functions f and smart_g will eventually be optimized, while naive_g will not.
Search for for loops
The decorator looks for standard for loops in the bytecode of the function , while while loops and for loops inside the generator and list expressions are ignored. Nested loops are not yet supported (only the innermost loop is optimized). For-else constructions are correctly processed .
Allowed Types
The decorator cannot optimize the loop no matter what types of variables are used in it. The fact is that, for example, Python allows you to determine the type that, with each multiplication, writes a string to a file. As a result of applying the optimization, the number of multiplications made in the function could change. Because of this, the number of lines in the file would be different and optimization would break the program.
In addition, when operations with matrices, variables are added and multiplied implicitly, so the types of variables can be “mixed up”. If one of the constants or variables would be of type float , those variables that should have been of type int after execution of the code could also be of type float (since adding intand float returns float ). Such behavior can cause errors in the program and is also unacceptable.
To avoid unwanted side effects, the decorator optimizes the loop only if all the constants and variables used in it are of a valid type. The initial valid types are int and long , as well as types inherited from them. If one of the constants or variables is of type long , those variables that should have been of type int after execution of the code can also be of type long . However, since int and longin Python are interchangeable enough, this should not lead to errors.
In case you want to change the set of valid types (for example, to add support for float ), you must pass a tuple of the required types in the types parameter . Types that are part of this tuple or inherited from types that are part of this tuple will be considered valid. In fact, checking that any value has a valid type will be performed using the expression isinstance (value, types) .
Cycle Optimization Conditions
Each cycle found must satisfy a number of conditions. Some of them are checked already when using the decorator:
- Тело цикла должно состоять только из инструкций присваивания, унарных и бинарных операций, которые могут быть скомпонованы в сложные выражения. Оно не может содержать условий, вызовов других функций, операторов return и yield и т. д..
- От операндов может требоваться условие предсказуемости: на каждой итерации цикла их значение должно быть одним и тем же, причём оно не должно зависеть от результатов каких-либо вычислений на предыдущей итерации. При этом:
- Все операнды сложения и вычитания, а также операнд унарного минуса могут быть непредсказуемыми.
- Хотя бы один операнд умножения должен быть предсказуем (аналогично тому, что в оригинальном интерпретаторе поддерживалось только умножение на константу).
- All operands of exponentiation, division and remainder operations, and bitwise operations must be predictable.
- All constants used in the loop must be of a valid type.
If these conditions are met, a “trap” is set before the cycle, which will check another part of the conditions, while the original byte code of the cycle is not deleted. Since Python uses dynamic typing, the following conditions can only be checked immediately before starting the loop:
- The object through which the loop passes must have the standard xrange type or its analogue from this cpmoptimize.xrange library . However, the slow range function that returns a list is not supported.
- The values of all variables used in the loop are of a valid type.
If the “trap” concluded that the optimization is acceptable, the necessary matrices will be calculated, and then the values of the variables used will be changed to new ones. If optimization cannot be performed, the original bytecode of the loop will be launched.
Expressions and code removal per cycle
Despite the fact that the described method does not support exponentiation and bitwise AND operations, the following code will be optimized:
@cpmoptimize()
def f(n, k):
res = 0
for i in xrange(n):
m = 3
res += ((k ** m) & 676) + i
return res
When analyzing the bytecode, the decorator concludes that the values of the variables k and m in the expression (k ** m) & 676 do not depend on which iteration of the cycle they are used, and therefore the value of the entire expression does not change. It is not necessary to calculate it at each iteration; it is enough to calculate this value once. Therefore, the corresponding bytecode instructions can be taken out and executed immediately before the start of the cycle, substituting the ready-made value in the cycle. The code will be converted to the following:
@cpmoptimize()
def f(n, k):
res = 0
m = 3
_const1 = (k ** m) & 676
for i in xrange(n):
res += _const1 + i
return res
This technique is known as the removal of the invariant code per cycle ( loop-invariant below code motion ). Please note that the values removed are calculated each time the function starts, as they may depend on changing global variables or function parameters (as _const1 in the example depends on the parameter k ). The resulting code is now easily optimized using matrices.
It is at this stage that the above predictability check is performed. For example, if one of the operands of the bitwise AND were unpredictable, this operation could no longer be taken out of the loop and optimization could not be applied.
The decorator also partially supports multiple assignments. If there are few elements in them, Python creates bytecode supported by the decorator without using tuples:
a, b = b, a + b
Threshold iters_limit
In the graphs above, you may have noticed that with a small number of iterations, the optimized cycle can work slower than usual, since in this case it still takes some time to construct the matrices and type check. In cases where it is necessary for the function to work as fast as possible and with a small number of iterations, you can explicitly set the threshold with the iters_limit parameter . Then the “trap” before starting the optimization will check how many iterations the loop has to complete and cancel the optimization if this number does not exceed the specified threshold.
Initially, the threshold is set to 5000 iterations. It cannot be set lower than in 2 iterations.
It is clear that the most favorable threshold value is the intersection point on the graph of lines corresponding to the operating time of the optimized and initial versions of the function. If the threshold is set exactly this way, the function will be able to choose the fastest algorithm in this case (optimized or initial):

Strict flag
In some cases, optimization should be mandatory. So, if in a loop of
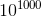 iterations, without optimization, the program simply freezes. In this case, the strict parameter is provided . Initially, its value is False , but if it is set to True , an exception will be thrown if one of the standard for loops has not been optimized.
iterations, without optimization, the program simply freezes. In this case, the strict parameter is provided . Initially, its value is False , but if it is set to True , an exception will be thrown if one of the standard for loops has not been optimized. If the fact that optimization is not applicable was detected at the stage of applying the decorator, an exception cpmoptimize.recompiler.RecompilationError will be immediately raised . In the example in the loop, two unpredictable variables are multiplied:
>>> from cpmoptimize import cpmoptimize
>>>
>>> @cpmoptimize(strict=True)
... def f(n, k):
... res = 0
... for i in xrange(n):
... res += i * res
... return res
...
Traceback (most recent call last):
File "", line 1, in
File "cpmoptimize/__init__.py", line 100, in upgrade_func
index += analyze_loop(settings, code, index) + 1
File "cpmoptimize/__init__.py", line 59, in analyze_loop
raise err
cpmoptimize.recompiler.RecompileError: Multiplication of two unpredictable values is unsupported
If that optimization is not applicable was detected before the loop execution (that is, if it turned out that the types of iterator values or variables are not supported), a TypeError exception will be thrown :
>>> from cpmoptimize import cpmoptimize
>>>
>>> @cpmoptimize(strict=True)
... def f(iterable):
... res = 0
... for elem in iterable:
... res += elem
... return res
...
>>> f(xrange(30))
435
>>> f(range(30))
Traceback (most recent call last):
File "", line 1, in
File "", line 4, in f
File "cpmoptimize/hook.py", line 170, in exec_loop
raise err
TypeError: Iterator in optimized loops must have type "xrange" instead of Additional Optimization Options
Two flags opt_min_rows and opt_clear_stack are responsible for the use of additional optimization methods when constructing matrices. Initially, they are turned on, the ability to turn them off is present only for demonstration purposes (thanks to it, you can compare the effectiveness of these methods).
When executing optimized code, the majority of the time is occupied by the multiplication of long numbers in some cells of the generated matrices. Compared to this time-consuming process, the time spent on multiplying all other cells is negligible.
In the process of recompiling expressions, the decorator creates intermediate, virtualvariables responsible for the position of the interpreter stack. After complex calculations, they may leave long numbers that are already stored in some other, real variables. We no longer need to store these values a second time, however, they remain in the cells of the matrix and significantly slow down the program, since when we multiply the matrices, we are forced to multiply these long numbers once again. The opt_clear_stack option is responsible for clearing such variables: if you assign them zero at the end of their use, long values disappear in them.
This option is especially effective when the program operates with very large numbers. The elimination of unnecessary multiplications of such numbers allows you to speed up the program more than twice. Opt_min_rows
optioninvolves minimizing the size of the square matrices that we multiply. Rows corresponding to unused and predictable variables are excluded from matrices. If the loop variable itself is not used, the rows responsible for maintaining its correct value are also excluded. In order not to disrupt the program, after the cycle, all these variables will be assigned the correct final values. In addition, in the original article, the vector of variables was supplemented by an element equal to unity. If the row corresponding to this element is unused, it will also be excluded.
This option can slightly speed up the program for not very large n , when the numbers have not yet become very long and the dimensions of the matrix make a significant contribution to the running time of the program.
If you use both options at the same time, then the virtual variables begin to have a predictable (zero) value, and opt_min_rows works even more efficiently. In other words, the effectiveness of both options together is greater than the effectiveness of each of them individually.
The graph below shows the operating time of the program for calculating Fibonacci numbers when disabling certain options (here "-m" is the program with opt_min_rows disabled , "-c" is the program with opt_clear_stack disabled , "-mc" is the program where both options are disabled immediately ):

What else can be implemented?
Change a set of operations
We will say that our method supports a couple of operations
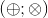 if:
if:- We can perform an operation
 for two variables or for a variable and a constant;
for two variables or for a variable and a constant; - We can perform an operation
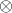 for a variable and a constant.
for a variable and a constant.
We already know that the method supports a couple of operations
 . Really:
. Really:- We can add two variables or a variable and a constant;
- We can multiply a variable by a constant.
It is these operations that are currently implemented in the optimizing decorator. However, it turns out that the described method supports other pairs of operations, including
 (a pair of multiplication and exponentiation).
(a pair of multiplication and exponentiation). For example, our task may be to find the nth number in the sequence specified by the recurrence relation:
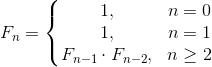
If our decorator supported a couple of operations
 , we could multiply the variable by another variable (but could not add the variables anymore). In this case, the following trivial solution to this problem could be accelerated by the decorator:
, we could multiply the variable by another variable (but could not add the variables anymore). In this case, the following trivial solution to this problem could be accelerated by the decorator:def f(n):
a = 1
b = 1
for i in xrange(n):
a, b = b, a * b
return a
We can prove that our method also supports pairs of operations
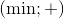 ,
,  and
and 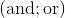 (here and is a bitwise AND, or is a bitwise OR). In the case of positive numbers, you can work with pairs of operations
(here and is a bitwise AND, or is a bitwise OR). In the case of positive numbers, you can work with pairs of operations 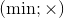 and
and 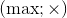 .
. To implement support for operations
 , for example, one can operate not with the values of variables, but with the logarithms of these values. Then the multiplication of variables will be replaced by the addition of logarithms, and the raising of a variable to a constant power will be replaced by the multiplication of the logarithm by a constant. Thus, we reduce the problem to the already realized case with operations
, for example, one can operate not with the values of variables, but with the logarithms of these values. Then the multiplication of variables will be replaced by the addition of logarithms, and the raising of a variable to a constant power will be replaced by the multiplication of the logarithm by a constant. Thus, we reduce the problem to the already realized case with operations  .
.The explanation of how to implement support for the remaining specified pairs of operations contains a certain number of mathematical calculations and is worthy of a separate article. At the moment, it is only worth mentioning that the pairs of operations are to some extent interchangeable.
Nested loops
By refining the loop analysis algorithm in bytecode, you can implement support for nested loops to optimize code like this:
def f():
res = 0
for i in xrange(10 ** 50):
for j in xrange(10 ** 100):
res += i * 2 + j
return res
Predictable conditions
In the following code, the condition in the loop body is predictable. Before starting the cycle, you can find out if it is true and remove the non-executing code branch. The resulting code can be optimized:
def f(mode):
res = 0
for i in xrange(10 ** 50):
if mode == 1:
res += 3
else:
res += 5
return res
conclusions
The Python interpreter, generally speaking, produces predictable bytecode that almost exactly matches the source code you wrote. By default, it does not perform any inlining of functions, nor unfolding of loops, nor any other optimizations that require analysis of program behavior. Only since version 2.6 did CPython learn to collapse constant arithmetic expressions, but this feature does not always work efficiently.
There are several reasons for this situation. Firstly, the analysis of code in the general case in Python is difficult, because data types can only be tracked during program execution (which we do in our case). Secondly, optimizations, as a rule, still do not allow Python to achieve the speed of purely compiled languages, therefore, in the case when the program needs to work very quickly, it is proposed to simply write it in a lower level language.
However, Python is a flexible language that allows you to implement many optimization methods yourself if necessary without interfering with the interpreter. This library, as well as other projects listed below, illustrate this opportunity well.
UPD. The project description is now also available as a presentation on SlideShare.
see also
Below I will provide links to several other interesting projects to speed up the execution of programs in Python:
- PyPy is an alternative Python interpreter with JIT compilation support , which allows, as a rule, to execute Python programs much faster. PyPy itself is written in RPython, for which a translator to C code is specially designed.
- Pyston is a new alternative Python interpreter that translates code into an intermediate LLVM representation from which it can be optimized using LLVM tools and executed using JIT compilation.
- Nuitka — компилятор Python. В отличие от упаковщика py2exe, который создаёт *.exe-файл, содержащий скрипт, интерпретатор и необходимые библиотеки, Nuitka действительно компилирует программы на Python в готовые исполняемые файлы.
- WPython — модифицированный интерпретатор CPython 2.6.4 с более эффективной моделью байт-кода, умной системой сворачивания констант и переработанной виртуальной машиной.
- astoptimizer — библиотека, применяющая известные методы оптимизации перед компиляцией в байт-код путём анализа и изменения абстрактного синтаксического дерева.
- promise — библиотека, оптимизирующая байт-код, полагаясь на так называемые «обещания». Если программист обещает не делать определённого рода операций в своём коде, становится возможным применить те оптимизации, которые в общем случае применить было нельзя.
- foldy.py — библиотека, анализирующая байт-код и выполняющая сворачивание констант (constant folding), то есть замену константных выражений на их значения, а также удаление неиспользуемых функций.
- Декоратор, анализирующий байт-код и выполняющий встраивание констант (constant binding), то есть заменяющий поиск значения постоянной глобальной переменной по её имени на непосредственную загрузку соответствующей константы.
UPD # 1. User magik suggested a few links:
- NumPy is a library (with Python modules written in C) that can quickly perform calculations with large arrays and matrices, as well as use an extensive set of high-level mathematical functions.
- Numba is a library that accelerates programs that contain mathematical calculations and operations with arrays. Optimization is due to JIT compilation (when using LLVM), which converts the code into native CPU and GPU instructions, as well as due to some other classical methods.
- Numexpr is a library that speeds up the calculation of mathematical expressions through analysis and modification of the corresponding bytecode. Expressions can be divided into several parts, some of which can be recalculated less often than others, accelerated by parallelization of the code, etc.
- Cython is an optimizing compiler of a superset of the Python language that allows you to use static typing in the program and interact closely with C and C ++ code.
- An article with an overview of libraries that accelerate a variety of calculations in Python due to JIT compilation.
UPD # 2. A DuneRat user pointed to several other Python compilation projects: shedskin , hope , pythran .
