Business Process Optimization with Survival Curves
Let's imagine that we have a restaurant reservation service. Booking takes place in 2 stages:
We want to understand how efficiently the call center works and how quickly applications are processed.
Good ways to analyze this are survival curves.
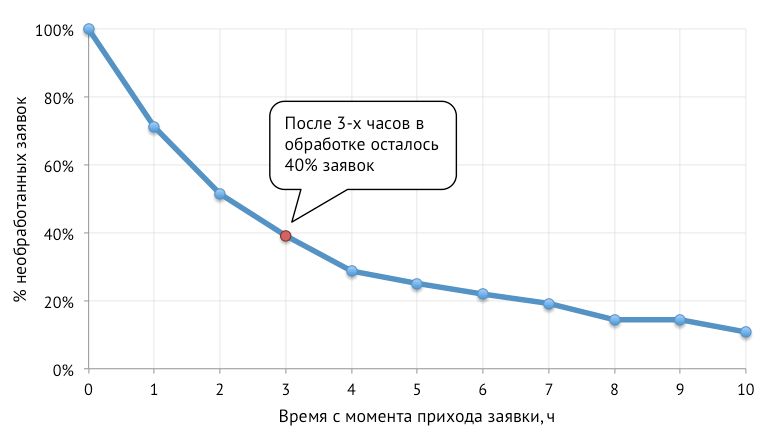
In our case, the survival curve is a graph showing% of unprocessed orders after a certain time.
The graph above shows the simplest example of a survival curve. We will consider more cunning options at the end of the article.
To build a survival curve, we need:
These data can be represented as follows:
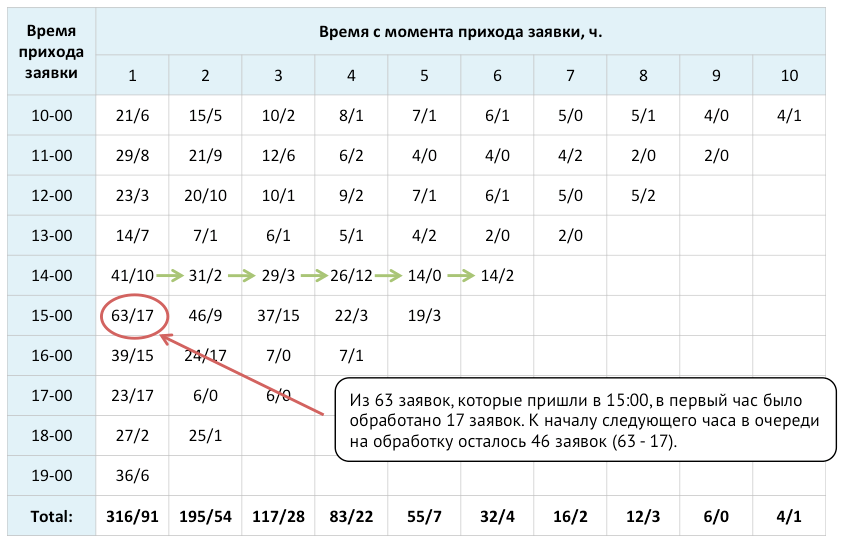
In each cell:
For example, out of 63 applications that arrived from 15:00 to 16:00, 17 applications were processed in the first hour, and by the beginning of the next hour 46 applications remained in the processing queue.
The bottom line of the table summarizes the total number of remaining applications from each group of the “same age”, as well as the total number of processed applications from the corresponding group.
Let's present the data from the last row in the form of the following table (calculations are given below): The
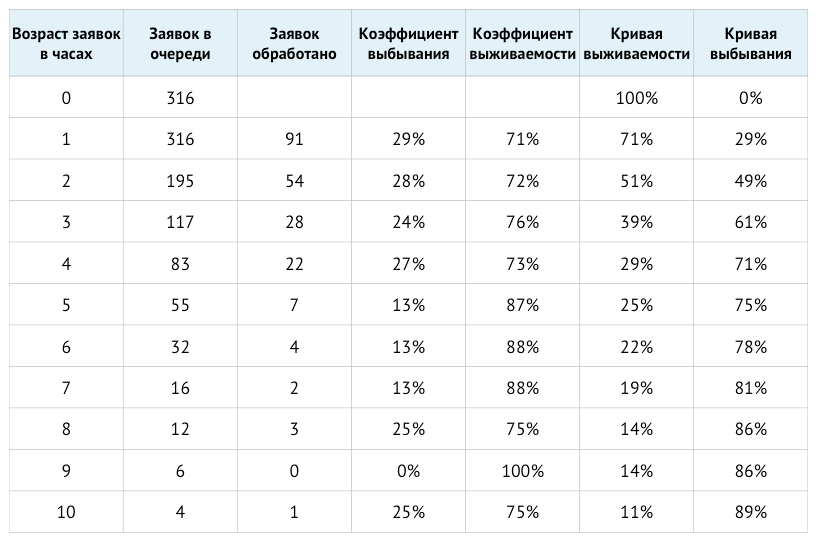
corresponding values from the table are calculated as follows : Dropout
rate [i] = Applications processed [i] / Applications in the queue [i]
Survival rate [i] = 1 - elimination coefficient [i]
curve survival [i] = survival rate [i] * survival curve [i-1]
Dropout curve [i] = 1 - Survival curve [i]
The survival curve constructed below starts with 100 percent of unprocessed applications at zero age:

It is more convenient to use the dropout curve for analysis. The dropout curve is the percentage of processed applications at the appropriate age. Do not confuse the dropout curve with the survival curve. In the first case, we look at the share of processed applications, in the second - unprocessed.
The corresponding dropout curve is plotted below:
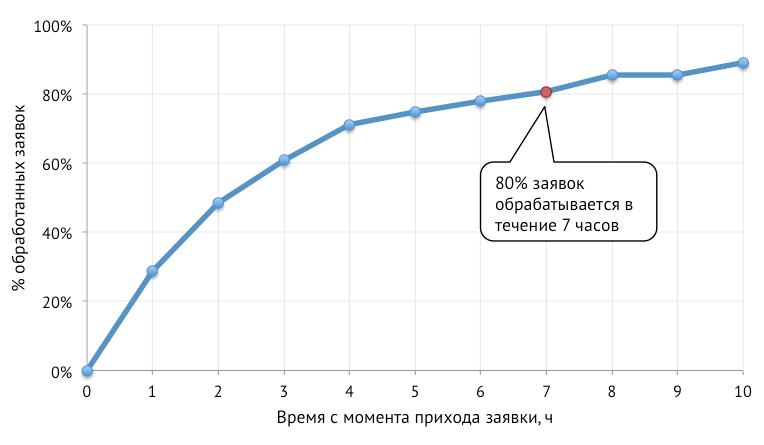
Further, for the analysis we will use the dropout curves.
Let's start with the last chart from the last paragraph. From it you can understand how quickly our call center processes applications. It can be seen that on average 80% of applications are processed within 7 hours.
If you build such survival curves not for the entire call center, but for each employee individually, then you can understand who works more efficiently. Based on these data, you can reward the best employees and dismiss / train the less efficient.
Let's look at another example:

From the graph it can be seen that reservation requests are not processed during the first two hours. The reasons for the delay may be different:
Let's look at such a schedule:
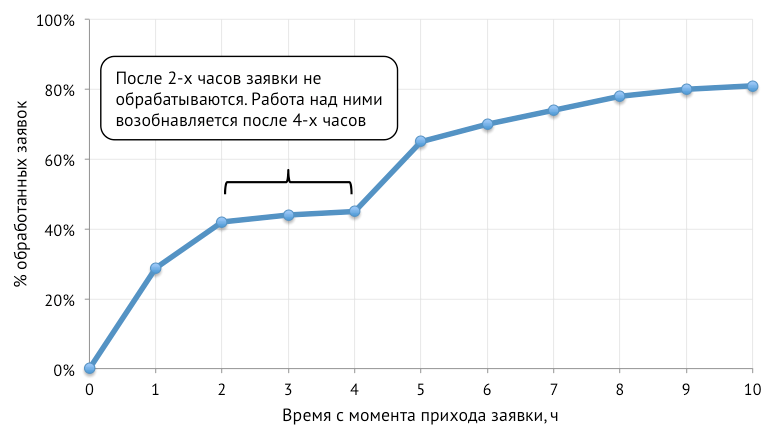
It can be seen that after 2 hours the applications are practically not processed, and work on them resumes only after 4 hours. The reasons may be as follows:
Each case must be dealt with separately. Elimination curves help to find bottlenecks, but additional efforts must be made to benefit:
- The user leaves a request to book a table on the site.
- Our call center calls back to the user to confirm or cancel the reservation.
We want to understand how efficiently the call center works and how quickly applications are processed.
Good ways to analyze this are survival curves.

What is a survival curve?
In our case, the survival curve is a graph showing% of unprocessed orders after a certain time.
The graph above shows the simplest example of a survival curve. We will consider more cunning options at the end of the article.
How to build survival curves?
To build a survival curve, we need:
- the number of applications received at the beginning of each hour;
- the number of processed applications for each hour.
These data can be represented as follows:

In each cell:
- the first number shows the number of unprocessed reservation requests available at the beginning of the hour;
- the second number shows the number of calls processed by the call center during this hour.
For example, out of 63 applications that arrived from 15:00 to 16:00, 17 applications were processed in the first hour, and by the beginning of the next hour 46 applications remained in the processing queue.
The bottom line of the table summarizes the total number of remaining applications from each group of the “same age”, as well as the total number of processed applications from the corresponding group.
Let's present the data from the last row in the form of the following table (calculations are given below): The

corresponding values from the table are calculated as follows : Dropout
rate [i] = Applications processed [i] / Applications in the queue [i]
Survival rate [i] = 1 - elimination coefficient [i]
curve survival [i] = survival rate [i] * survival curve [i-1]
Dropout curve [i] = 1 - Survival curve [i]
The survival curve constructed below starts with 100 percent of unprocessed applications at zero age:

It is more convenient to use the dropout curve for analysis. The dropout curve is the percentage of processed applications at the appropriate age. Do not confuse the dropout curve with the survival curve. In the first case, we look at the share of processed applications, in the second - unprocessed.
The corresponding dropout curve is plotted below:

How to analyze?
Further, for the analysis we will use the dropout curves.
Let's start with the last chart from the last paragraph. From it you can understand how quickly our call center processes applications. It can be seen that on average 80% of applications are processed within 7 hours.
If you build such survival curves not for the entire call center, but for each employee individually, then you can understand who works more efficiently. Based on these data, you can reward the best employees and dismiss / train the less efficient.
Let's look at another example:

From the graph it can be seen that reservation requests are not processed during the first two hours. The reasons for the delay may be different:
- We may not have enough people in the call center, and old applications are processed first.
- Restaurants can confirm the reservation with a delay, and our call center processes the application only after confirmation from the restaurant.
- Applications from the site database can be downloaded for dialing once every 2 hours.
- Perhaps the delay is due to the specifics of our service.
Let's look at such a schedule:

It can be seen that after 2 hours the applications are practically not processed, and work on them resumes only after 4 hours. The reasons may be as follows:
- If the call center cannot reach the customer, he will postpone the attempt to dial up for 4 hours.
- Some restaurants confirm the reservation later, and the call center may process the reservation of such restaurants with a delay.
- Perhaps the first attempt to dial is made automatically, and if the call did not take place, then after 4 hours the application is unloaded for manual dialing.
What's next?
Each case must be dealt with separately. Elimination curves help to find bottlenecks, but additional efforts must be made to benefit:
- Bonus or fire employees.
- Agree on a more rapid response of partners.
- Change the process of processing applications.
