10 entertaining tasks

Illustration for the last task.
There are problems with simple and seemingly obvious solutions, which, however, are difficult to find. When solving them, it is dangerous to rely on intuition, because the correct answer often does not at all coincide with the one that it prompts. In this article, I offer a selection of 10 such tasks, sorted by increasing complexity; their decisions are removed under the spoiler. To get the right answers you do not need to have any special knowledge, just resourcefulness and knowledge of the school curriculum are enough.
- From the cities A and B, the distance between which is 100 km, two trains leave at the same time to meet each other, their speeds are 40 km / h and 60 km / h, respectively. At the same time, a fly at a speed of 200 km / h flies from city A to direction B, flies before meeting a train leaving B, then flies to a train leaving A, then flies again to a train leaving B, etc. d. How far will the fly fly before the trains meet?DecisionThe train approach speed is 100 km / h, the distance between them is 100 km, which means they will meet in 1 hour. The fly will fly during this hour at a speed of 200 km / h and fly a total of 200 km .
- In triangle ABC, angle C is straight, BM is median. Prove: ∠CAB> ∠ABM.
 EvidenceIn the triangle of MBC, the leg of CM is smaller than the hypotenuse of BM. MC = AM. Hence MB> AM. Consider a triangle ABM, in which the side MB is larger than the side AM. On the contrary, the larger side has a larger angle. Hence ∠CAB> ∠ABM. Chtd.
EvidenceIn the triangle of MBC, the leg of CM is smaller than the hypotenuse of BM. MC = AM. Hence MB> AM. Consider a triangle ABM, in which the side MB is larger than the side AM. On the contrary, the larger side has a larger angle. Hence ∠CAB> ∠ABM. Chtd. - Citizens of a country live for a long time according to the following rules: the family gives birth to children until the first boy, after which children are not born in the family. Only boys and girls are born with equal probabilities; twins are not born. Determine the proportion of male population in this country. Assume that mortality is not dependent on gender.DecisionThe task is a trap. The rule “there is exactly one boy in the family” does not affect the likelihood of having a boy as a whole in the country. Correct answer: 50% .
- Two girlfriends at the same time begin to do homework, and each of them solves seven problems per hour with a resolver, and without it - only four. Which of the girls would be freed earlier if the first schoolgirl gave the solitary to her friend after completing half of the assignment?DecisionWe assume that the entire task consists of 28 tasks. The first one will solve half of the task (14 problems) with the resolver in 14/7 = 2 hours, and the second will solve 2 * 4 = 8 problems during this time. Armed with a resolver, the second will solve the remaining 28-8 = 20 problems in 20/7 <3 hours, and the first during this time will solve only 3 * 4 = 12 problems, and in all she will have 14 problems. Therefore, earlier the second girl will cope with the task.
- Iron scrap lies on a piece of ice that floats in the pool. How will the water level in the pool change when the ice melts (and the scrap drowns)?DecisionWe recall the law of Archimedes: a buoyant force acts on a body immersed in a liquid, equal to the force of gravity of the liquid displaced by this body. It should be noted that the body must be completely surrounded by liquid or intersect with the surface of the liquid. So, for example, the law of Archimedes cannot be applied to a scrap that lies at the bottom of the pool. Thus, while ice and scrap are floating, the mass of scrap and ice is equal to the mass of displaced water. When the scrap sinks to the bottom, the volume of water displaced by it is equal to the volumescrap. The mass of ice is equal to the mass of water into which it turned when it melted, so the contribution of ice can be ignored. (By the way, for the same reason, if scrap was not included in the original problem, the answer would be that the water level does not change.) Before melting, the crowding crowded out more water than after melting, since water has a lower density than scrap. Answer: the water level in the pool will drop . (If we assume that ice and scrap floated in the water column, and not on the surface, then the rationale is completely simplified: the volume of ice decreased when the ice melted, and the volume of scrap did not change.)
- The number n is a positive integer, the number p is a prime, prove that it
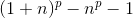 is divisible by p. (Knowledge of the basics of combinatorics is required.)EvidenceRecall Newton’s bin .
is divisible by p. (Knowledge of the basics of combinatorics is required.)EvidenceRecall Newton’s bin .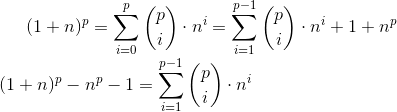
In the last expression, each binomial coefficient is divided by p, since p is prime and is in the numerator in the formula of the binomial coefficient , and in the denominator is the product of numbers less than p. Chtd. - The puzzle "Hanoi Towers" consists of three rods, numbered 1, 2, 3. On rod 1 is a pyramid of N disks of different diameters in increasing diameter. Disks can be transferred from one rod to another one at a time, while the disk cannot be placed on a disk of a smaller diameter. It is necessary to shift the entire pyramid from rod 1 to rod 3.
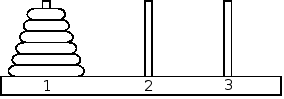
Solution
ejudge-check solution - How many different lines of length N are there, consisting of the characters “0” and / or “1”, in which two units do not go in a row? The answer may be a recurrence formula.DecisionLet F (N) denote the number of rows of length N that do not contain two units in a row. Denote by F0 (N) the number of lines of length N that do not contain two units in a row and ending with 0. Denote F1 (N) the number of lines of length N that do not contain two units in a row and ending with 1. We
derive recurrence formulas for F0 and F1.
F1 (N) = F0 (N-1). Since there cannot be two units in a row, the number of lines ending with 1 is equal to the number of lines 1 smaller in length ending in 0.
F0 (N) = F0 (N-1) + F1 (N-1). Zero can be added to any correct line without violating the conditions. Therefore, the number of lines ending in 0 is equal to the number of lines in 1 shorter length.
F0 (N) = F0 (N-1) + F1 (N-1) = F0 (N-1) + F0 (N-2). So, F0 is a Fibonacci series with a certain shift. F1 (N) = F0 (N-1), which means F1 also consists of Fibonacci numbers, with a “lag” of 1 relative to F0.
F (N) = F0 (N) + F1 (N). The term F (N) is obtained when the number from the Fibonacci series F0 is added to the number from the Fibonacci series F1, which is the previous number for it. And the sum of the Fibonacci number with the previous Fibonacci number is also the Fibonacci number (according to the formula of Fibonacci numbers). So, we have proved that the number of rows that do not include two units in a row will be the Fibonacci number . It remains to determine the value of F (N) for the first two N. F (1) = 2 (two suitable sequences: “0” and “1”), F (2) = 3 (three suitable sequences: “00”, “01” , "10").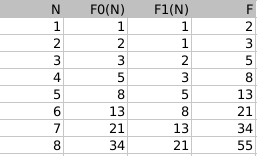
- The shareholders sat at a round table on which plates with their names were installed (one share for each shareholder). However, everyone sat down at a sign with a strange name. Prove that you can rotate the table so that at least 2 shareholders are sitting at their tablets.EvidenceThe key condition is the fact that at first not a single shareholder sits behind his sign. Let the number of shareholders be equal to N. The number of table states is also N. At one of the table states (initial), no shareholder sits at his plate; therefore, the table conditions under which shareholders can be compared with tablets are N-1. We will go over these N-1 states. During this time, all N shareholders must "go" for their signs. According to the Dirichlet principle , at least one of the N-1 states being searched must have at least two of N comparisons. In other words, there is a condition in which at least two shareholders are sitting at their signs. Chtd.
- N sages lined up with a “train”, each wearing a cap of white or black. Each sage hears what they say around, and sees the colors of the caps in front of the standing sages, but does not see his cap and the caps of the sages standing in the back. All of them in turn, starting with the last one, are asked the question: “What color is the cap on you?”. A sage is allowed to answer only “white” or “black”. Develop an algorithm for the actions of sages such that the number of correct answers is at least N-1.DecisionDenote the white cap by one, the black cap by zero. The last sage adds up the colors of the caps in front of the standing sages modulo 2 (Xorit them). Names the color corresponding to the resulting amount. The further fate of the last sage is not so interesting: perhaps the named color coincided with the color of his cap, maybe not. The next sage, after calculating the sum of the caps in front of them, adds it up with the color called the last sage, and gets the color of his cap, which he calls. The next one adds up three numbers: the number of white caps standing in front and the numbers said by the two previous sages. Subsequent sages act in the same way. It turns out at least N-1 correct answers.

Please inform me in the comments about alternative ways of completing tasks, including more complex or unsuccessful ones, as well as about errors and typos found.
Have a nice decision!
UPD . makaroni4 created a test from some tasks. Thanks!
Only registered users can participate in the survey. Please come in.
How many tasks did you solve?
- 19.6% 8-10 107
- 22.7% 5-7 124
- 20.1% 3-4 110
- 37.4% 0-2 204
Interesting tasks
- 51% 1 151
- 20.9% 2 62
- 46.6% 3 138
- 29.3% 4 87
- 41.5% 5 123
- 11.8% 6 35
- 20.6% 7 61
- 23.3% 8 69
- 39.5% 9 117
- 53% 10 157
