Particular solution to the general problem of electrostatics

From school, we remember the solution to the problem of the distribution of electric charge over an infinite conducting plane in the presence of a point electric charge over the plane. Only some will remember how the problem of the distribution of electric charge over a conducting sphere is analytically solved if a point charge rests somewhere in space. But, I am sure, no one will be able to solve the similar problem of the distribution of charge in a Klein bottle. If we add an external electrostatic field and other conductors to such a system, it would be foolish to even dream of an analytical solution.
We formulate the general problem of electrostatics as follows:
Given:
- the shape and location of conductors in space
- charge of conductors
- external electric field (field in the absence of conductors, independent of the position of the conductors)
It is necessary to find the charge distribution over the surface of the conductors and the scalar potential of the electric field throughout the space .
The potential as a function of three Cartesian coordinates must satisfy the Poisson equation in the whole space:
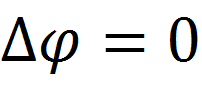
From the uniqueness theorem it follows that if we find a function that satisfies this equation and the boundary conditions, i.e. solution, this solution will be the only one.
To avoid unnecessary complexity, consider the solutionproblems of the distribution of electric charge over a conductive surface in the presence of an external field independent of the position and charge of the conductive surface.
We will seek a solution to the problem numerically by the finite element method.
I’ll immediately warn that I will not theoretically consider the question of the convergence of my method, but will limit myself to only a few facts from practice, testifying in favor of the hypothesis of convergence of this method, although it may not be a true solution.
Define the surface parametrically:
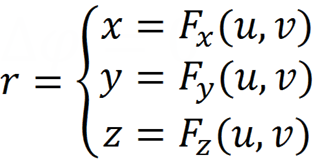
Choose the number of u and v partitions and cover the surface with the network u and v- lines. At the nodes of the resulting grid, we place electric charges, the value of which we have to find.
We also select Nu * Nv points in the immediate vicinity of the nodes. We will seek a solution based on the condition that the potential of the electric field at these points is the same. The potential itself will be calculated as a superposition of potentials created by point charges.
We compose the matrices:
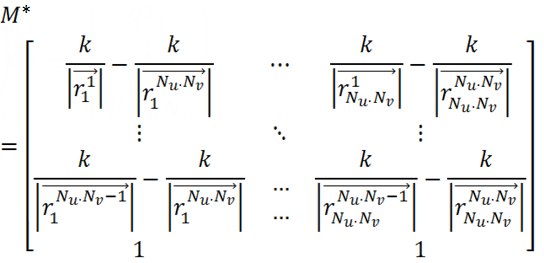
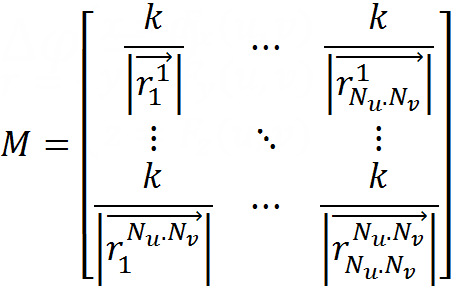 - a sketch of the matrix of the linear system, which we will solve. The lower indices indicate the position of the charges, the upper indices indicate the points of consideration of the potential. These distances are found from the parameterization of the surface.
- a sketch of the matrix of the linear system, which we will solve. The lower indices indicate the position of the charges, the upper indices indicate the points of consideration of the potential. These distances are found from the parameterization of the surface. 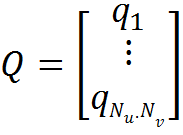 - column matrix of unknowns - values of charges.
- column matrix of unknowns - values of charges. 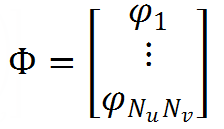 - the column matrix of the potentials of the external field at the points of consideration of the potential.
- the column matrix of the potentials of the external field at the points of consideration of the potential.Then we get the system Φ + MQ = A , where A is a certain constant column matrix composed of surface potentials unknown to us.
To exclude this potential from the system, we first transfer the matrix Φ to the right side of the equality, and then subtract from Nu * Nv-1 the first equations of the system the last equation, which is replaced by the normalization condition (the sum of all charges on the surface is equal to the total charge).
Then we get the final linear system with the system matrix:
And a column of free terms:
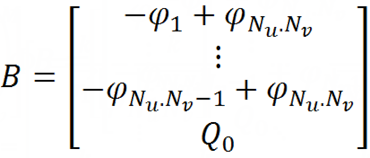
To end these pictures with an excessively large font, I will give the last expression defining the result of all the work - a piecewise constant function of the surface of the charge on the surface (meaning that for u and v belonging to the approximation area with the same indices, the function takes the value of the left side expressions):
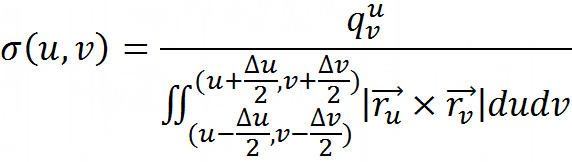
We will solve the system and work with the result in the Mathematica system.
A particular solution to the general problem of electrostatics.nb
Now let's look at the method. We start with a square plate parameterized in a trivial way. Then the parameters u and v are the Cartesian coordinates of the plate points and the area element, which stands under the integral above is equal to unity.
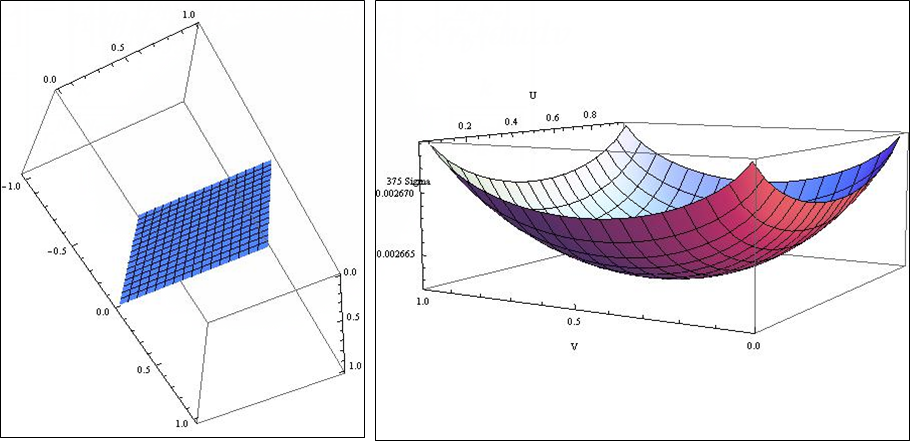
We got a logical and expected solution.
The solution for the sphere should be a plane, but we get something completely bad:

But it is not all that bad. With an increase in the number of nodes, this figure shrinks (on the automatically generated mathematics graph this, however, is not visible) and, I suppose, tends to take the place of the plane.
Surfaces for which a solution is being sought must be closed, otherwise a singularity at the edges can occur: with increasing accuracy, the charge density at the edges tends to infinity.
I also decided to solve the problem of the distribution of charge in a semicircle (“beads”) in two ways to test the operation of the method.
Method 1. Place the same charges on the beads. Inertialess charges. Let them go. In small steps they will take a stable position. Such a visual method of Zeidel type with respect to the angular coordinate of charges:

Method 2. The semi-cylinder in three-dimensional space corresponds to the above system, for which the problem will be solved by our method:

Externally, the solutions are very similar.
It is interesting to hear your opinion on the above method of solving the general problem of electrostatics.
