A simple introduction to the ALU for neural networks: an explanation, physical meaning and implementation
- Transfer
Recently, researchers from Google DeepMind, including a renowned scientist in the field of artificial intelligence, the author of the book “ Understanding Deep Learning, ” Andrew Trask, published an impressive article that describes a neural network model for extrapolating the values of simple and complex numerical functions with a high degree of accuracy.
In this post I will explain the architecture of NALU (neural arithmetic logic devices , NALU), their components and significant differences from traditional neural networks. The main goal of this article is to simply and intuitively explain NALU (and the implementation, and the idea) for scientists, programmers and students who are not familiar with neural networks and deep learning.
Note from the author: I also highly recommend reading the original article for a more detailed study of the topic.
The image is taken from this article.
In theory, neural networks should approximate functions well. They are almost always able to identify significant matches between input data (factors or features) and output (labels or targets). That is why neural networks are used in many areas, from object recognition and classification to speech-to-text translation and the implementation of game algorithms that can beat world champions. Many different models have already been created: convolutional and recurrent neural networks, auto-encoders, etc. Progress in creating new models of neural networks and in-depth learning is in itself a big topic to learn.
However, according to the authors of the article, neural networks do not always cope with tasks that seem obvious to people and even to bees.! For example, this is a verbal account or operations with numbers, as well as the ability to detect dependence from relationships. The article showed that the standard models of neural networks do not even cope with the identical mapping (a function that translates the argument into itself,
) - the most obvious numerical value. The figure below shows the MSE of various models of neural networks when learning the values of this function.
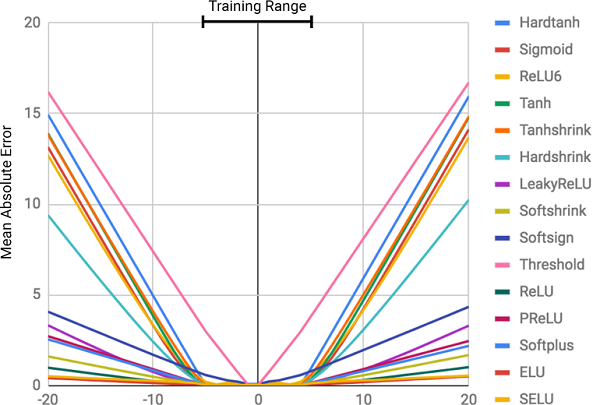
The figure shows the root mean square error for standard neural networks using the same architecture and different (non-linear) activation functions in the inner layers
As can be seen from the figure, the main cause of misses is the nonlinearity of the activation functions on the inner layers of the neural network. This approach works great for determining non-linear relationships between input data and responses, but it terribly makes mistakes when going beyond the limits of the data on which the network studied. Thus, neural networks do an excellent job of memorizing numerical dependencies from the training data, but they do not know how to extrapolate it.
This is similar to cramming an answer or a topic before an exam without understanding the essence of the subject being studied. It is easy to pass the test, if the questions are similar to homework, but if it is the understanding of the subject that is checked, and not the ability to memorize, we will fail.
This was not in the course program!
The degree of error is directly related to the level of nonlinearity of the selected activation function. The previous diagram clearly shows that nonlinear functions with hard constraints, such as sigmoid ( Sigmoid ) or hyperbolic tangent ( Tanh ), cope with the task of generalizing dependencies much worse than functions with soft constraints, such as truncated linear transformation ( ELU , PReLU ).
The Neural Battery ( NAC ) is at the core of the NALU model . It is a simple but effective part of the neural network that handles addition and subtraction , which is necessary for efficiently calculating linear connections.
NAC is a special linear layer of the neural network, on the weights of which a simple condition is imposed: they can take only 3 values - 1, 0 or -1 . Such restrictions do not allow the battery to change the range of input data values, and it remains constant across all layers of the network, regardless of their number and connections. Thus, the output is a linear combination of the values of the input vector, which can easily represent addition and subtraction operations.
Thinking out loud : for a better understanding of this statement, let us consider an example of constructing layers of a neural network that perform linear arithmetic operations on input data.
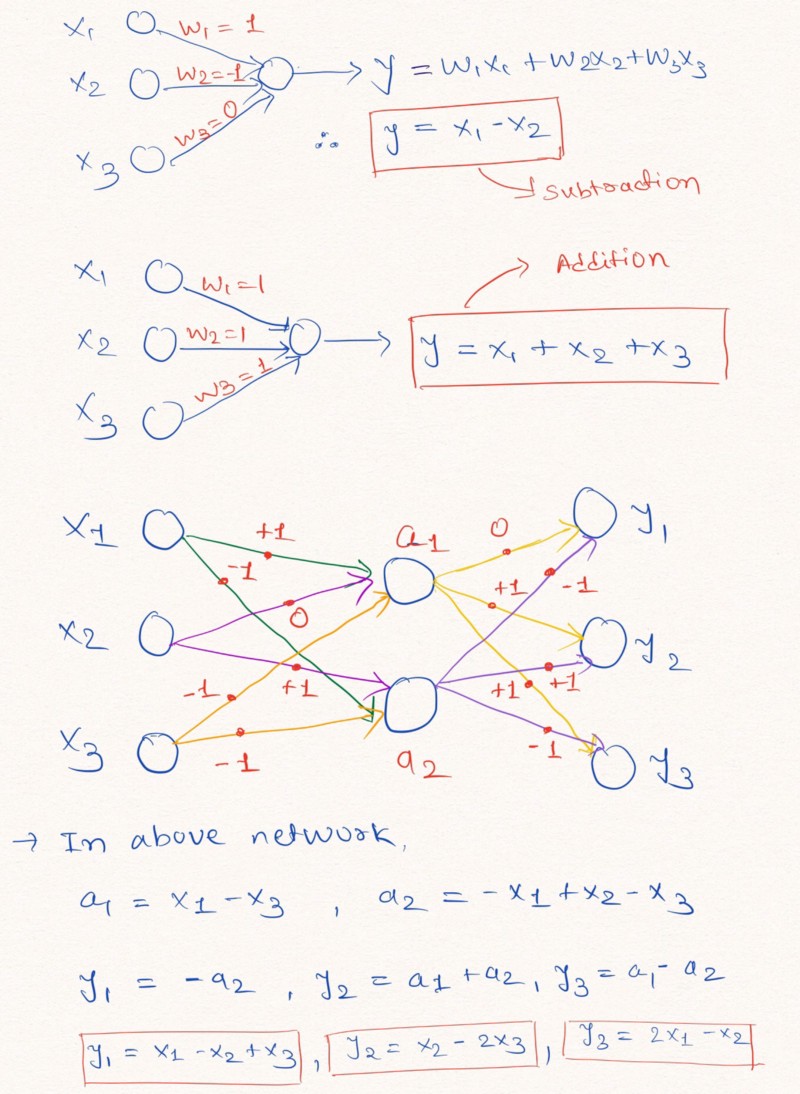
The figure explains how the layers of a neural network without adding a constant and with possible weights of -1, 0 or 1 can perform linear extrapolation.
As shown above in the image of layers, a neural network can learn to extrapolate the values of such simple arithmetic functions as addition and subtraction (
and 
), with the help of weight limits possible values of 1, 0 and -1.
Note: The NAC layer in this case does not contain a free term (constant) and does not apply non-linear transformations to the data.
Since standard neural networks do not cope with the solution of the problem with such restrictions, the authors of the article offer a very useful formula for calculating such parameters through classical (unlimited) parameters
and 
. Weight data, like all parameters of neural networks, can be initialized randomly and selected in the process of network training. Formula to calculate the vector
through and looks like that:
Using this formula ensures the boundedness of the range of values of W by the segment [-1, 1], which is closer to the set -1, 0, 1. Also, the functions from this equation are differentiable by weight parameters. Thus, our NAC layer will be easier to learn the valuesusing gradient descent and back propagation errors . Below is a diagram with the architecture of the NAC layer .
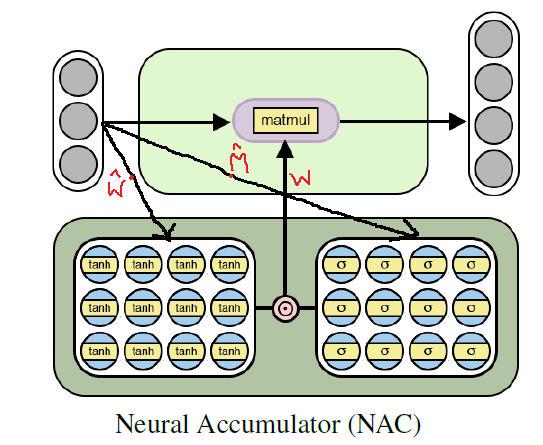
Neural accumulator architecture for learning on elementary (linear) arithmetic functions
As we have already understood, NAC is a fairly simple neural network (network layer) with small features. Below is the implementation of a single NAC layer in Python using the Tensoflow and NumPy libraries.
In the given code and are initialized using a uniform distribution, but you can use any recommended method of generating an initial approximation for these parameters. You can see the full version of the code in my GitHub repository (the link is duplicated at the end of the post).
Although the simple model of a neural network described above copes with simple operations like addition and subtraction, we need to be able to learn on the set of values of more complex functions, such as multiplication, division and exponentiation.
The following is a modified NAC architecture that is adapted for selecting more complex arithmetic operations through logarithmization and taking exponents within the model. Note the differences in this NAC implementation from those already discussed above. NAC
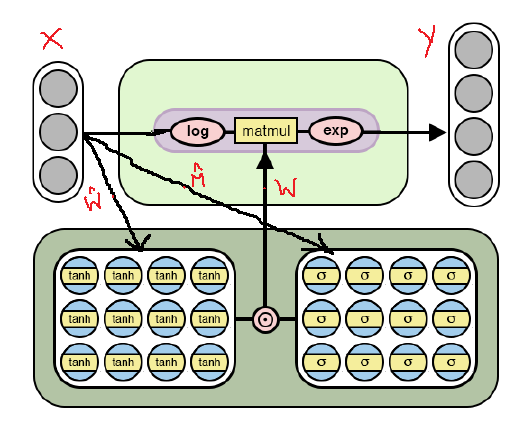
architecture for more complex arithmetic operations
As can be seen from the figure, we logarithm the input data before multiplying by the weights matrix, and then we calculate the exponent of the result obtained. The formula for calculations is as follows:
here it is a very small number to prevent log (0) situations during training.
Thus, for both NAC models, the principle of operation, including the calculation of a weights matrix with constraints through and , does not change. The only difference is the use of logarithmic operations on the input and output in the second case.
The code, like the architecture, is almost unchanged, with the exception of these improvements in the calculations of the tensor of output values.
Again I remind you that you can find the full version of the code in my GitHub repository (the link is duplicated at the end of the post).
As many have already guessed, we can learn almost any arithmetic operation, combining the two models discussed above. This is the main idea of NALU , which includes a weighted combination of elementary and complex NAC , controlled through a training signal. Thus, NAC are the building blocks for the assembly of NALU , and if you understand their device, it will be easy to build NALU . If you still have questions, try again to read the explanations for both NAC models . Below is a diagram with the NALU architecture . NALU
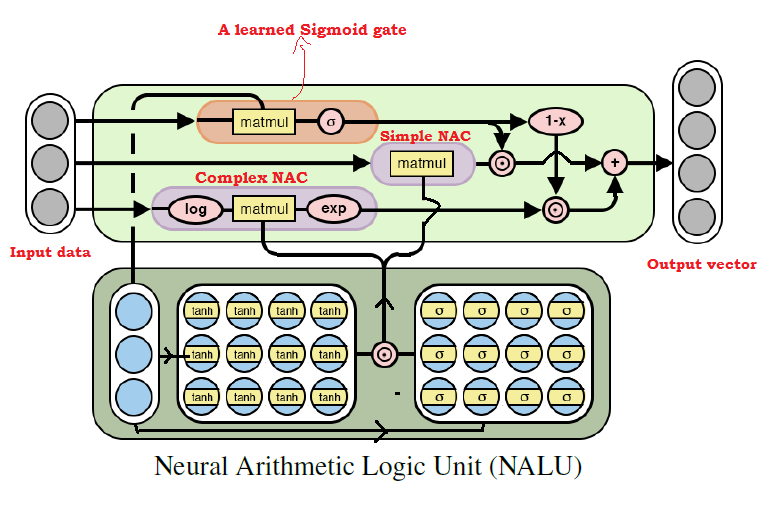
architecture diagram with explanations
As can be seen from the figure above, both NAC blocks (purple blocks) inside NALU are interpolated (combined) through a sigmoid of the training signal (orange block). This allows (de) to activate the output of any of them, depending on the arithmetic function, the values of which we are trying to find.
As mentioned above, the elementary NAC unit is an accumulating function, which allows NALU to perform elementary linear operations (addition and subtraction), while the complex NAC unit is responsible for multiplication, division, and exponentiation. The output in NALU can be represented as a formula:
From the formula NALU above, we can conclude that when
the neural network will only select values for complex arithmetic operations, but not for elementary ones; and vice versa - in the case of
. Thus, in general, NALU is able to study any arithmetic operation consisting of addition, subtraction, multiplication, division and exponentiation and successfully extrapolate the result beyond the limits of the initial data values.
In the implementation of NALU, we will use elementary and complex NAC , which we have previously defined.
Once again, in the code above, I again initialized the parameter matrix
using a uniform distribution, but you can use any recommended method of generating an initial approximation.
For me personally, the idea of NALU is a serious breakthrough in the field of AI, especially in neural networks, and it looks promising. This approach can open doors to those areas of application where standard neural networks could not cope.
The authors of the article talk about various experiments using NALU : from selecting the values of elementary arithmetic functions to counting the number of handwritten numbers in a given series of MNIST images , which allows neural networks to check computer programs!
The results make a tremendous impression and prove that NALU copes with almost any task.associated with the numerical representation, better than standard models of neural networks. I recommend that readers familiarize themselves with the results of the experiments in order to better understand how and where the NALU model can be useful.
However, it must be remembered that neither NAC nor NALU are the ideal solution for any task. They rather represent a general idea of how to create models for a particular class of arithmetic operations.
Below is a link to my GitHub repository, which contains the full implementation of the code from the article.
github.com/faizan2786/nalu_implementation
You can independently test the operation of my model on various functions by selecting hyper parameters for the neural network. Please ask questions and share your thoughts in the comments under this post, and I will do my best to answer you.
PS (from the author): this is my first ever written post, so if you have any tips, suggestions and recommendations for the future (both technical and general plan), please write to me.
PPS (from translator): if you have comments to the translation or to the text, please write me a personal message. I am particularly interested in the formulation for the learned gate signal - I am not sure that I was able to accurately translate this term.
In this post I will explain the architecture of NALU (neural arithmetic logic devices , NALU), their components and significant differences from traditional neural networks. The main goal of this article is to simply and intuitively explain NALU (and the implementation, and the idea) for scientists, programmers and students who are not familiar with neural networks and deep learning.
Note from the author: I also highly recommend reading the original article for a more detailed study of the topic.
When are neural networks wrong?
The image is taken from this article.
In theory, neural networks should approximate functions well. They are almost always able to identify significant matches between input data (factors or features) and output (labels or targets). That is why neural networks are used in many areas, from object recognition and classification to speech-to-text translation and the implementation of game algorithms that can beat world champions. Many different models have already been created: convolutional and recurrent neural networks, auto-encoders, etc. Progress in creating new models of neural networks and in-depth learning is in itself a big topic to learn.
However, according to the authors of the article, neural networks do not always cope with tasks that seem obvious to people and even to bees.! For example, this is a verbal account or operations with numbers, as well as the ability to detect dependence from relationships. The article showed that the standard models of neural networks do not even cope with the identical mapping (a function that translates the argument into itself,
) - the most obvious numerical value. The figure below shows the MSE of various models of neural networks when learning the values of this function. The figure shows the root mean square error for standard neural networks using the same architecture and different (non-linear) activation functions in the inner layers
Why are neural networks wrong?
As can be seen from the figure, the main cause of misses is the nonlinearity of the activation functions on the inner layers of the neural network. This approach works great for determining non-linear relationships between input data and responses, but it terribly makes mistakes when going beyond the limits of the data on which the network studied. Thus, neural networks do an excellent job of memorizing numerical dependencies from the training data, but they do not know how to extrapolate it.
This is similar to cramming an answer or a topic before an exam without understanding the essence of the subject being studied. It is easy to pass the test, if the questions are similar to homework, but if it is the understanding of the subject that is checked, and not the ability to memorize, we will fail.
This was not in the course program!
The degree of error is directly related to the level of nonlinearity of the selected activation function. The previous diagram clearly shows that nonlinear functions with hard constraints, such as sigmoid ( Sigmoid ) or hyperbolic tangent ( Tanh ), cope with the task of generalizing dependencies much worse than functions with soft constraints, such as truncated linear transformation ( ELU , PReLU ).
Solution: Neural Battery (NAC)
The Neural Battery ( NAC ) is at the core of the NALU model . It is a simple but effective part of the neural network that handles addition and subtraction , which is necessary for efficiently calculating linear connections.
NAC is a special linear layer of the neural network, on the weights of which a simple condition is imposed: they can take only 3 values - 1, 0 or -1 . Such restrictions do not allow the battery to change the range of input data values, and it remains constant across all layers of the network, regardless of their number and connections. Thus, the output is a linear combination of the values of the input vector, which can easily represent addition and subtraction operations.
Thinking out loud : for a better understanding of this statement, let us consider an example of constructing layers of a neural network that perform linear arithmetic operations on input data.
The figure explains how the layers of a neural network without adding a constant and with possible weights of -1, 0 or 1 can perform linear extrapolation.
As shown above in the image of layers, a neural network can learn to extrapolate the values of such simple arithmetic functions as addition and subtraction (
and ), with the help of weight limits possible values of 1, 0 and -1. Note: The NAC layer in this case does not contain a free term (constant) and does not apply non-linear transformations to the data.
Since standard neural networks do not cope with the solution of the problem with such restrictions, the authors of the article offer a very useful formula for calculating such parameters through classical (unlimited) parameters
and . Weight data, like all parameters of neural networks, can be initialized randomly and selected in the process of network training. Formula to calculate the vector through and looks like that:
Using this formula ensures the boundedness of the range of values of W by the segment [-1, 1], which is closer to the set -1, 0, 1. Also, the functions from this equation are differentiable by weight parameters. Thus, our NAC layer will be easier to learn the values
using gradient descent and back propagation errors . Below is a diagram with the architecture of the NAC layer . Neural accumulator architecture for learning on elementary (linear) arithmetic functions
Implementing NAC in Python using Tensorflow
As we have already understood, NAC is a fairly simple neural network (network layer) with small features. Below is the implementation of a single NAC layer in Python using the Tensoflow and NumPy libraries.
Python code
import numpy as np
import tensorflow as tf
# Определение нейронного аккумулятора (NAC) для сложения/вычитания# -> Помогает при подборе операций сложения/вычитанияdefnac_simple_single_layer(x_in, out_units):'''
Принимаемые параметры:
x_in -> Входной тензор X
out_units -> размер выходного вектора
Возвращаемые значения:
y_out -> Результирующий тензор заданной размерности
W -> Матрица весов для слоя
'''# Определяем количество строк во входных данных
in_features = x_in.shape[1]
# инициализируем W_hat и M_hat
W_hat = tf.get_variable(shape=[in_shape, out_units],
initializer=tf.initializers.random_uniform(minval=-2, maxval=2),
trainable=True,
name='W_hat')
M_hat = tf.get_variable(shape=[in_shape, out_units],
initializer=tf.initializers.random_uniform(minval=-2, maxval=2),
trainable=True,
name='M_hat')
# Считаем W по формуле
W = tf.nn.tanh(W_hat) * tf.nn.sigmoid(M_hat)
y_out = tf.matmul(x_in, W)
return y_out, W
In the given code
and are initialized using a uniform distribution, but you can use any recommended method of generating an initial approximation for these parameters. You can see the full version of the code in my GitHub repository (the link is duplicated at the end of the post).Moving on: from addition and subtraction to NAC for complex arithmetic expressions
Although the simple model of a neural network described above copes with simple operations like addition and subtraction, we need to be able to learn on the set of values of more complex functions, such as multiplication, division and exponentiation.
The following is a modified NAC architecture that is adapted for selecting more complex arithmetic operations through logarithmization and taking exponents within the model. Note the differences in this NAC implementation from those already discussed above. NAC
architecture for more complex arithmetic operations
As can be seen from the figure, we logarithm the input data before multiplying by the weights matrix, and then we calculate the exponent of the result obtained. The formula for calculations is as follows:
here it is a very small number to prevent log (0) situations during training.Thus, for both NAC models, the principle of operation, including the calculation of a weights matrix with constraints
through and , does not change. The only difference is the use of logarithmic operations on the input and output in the second case.Second version of NAC in Python using Tensorflow
The code, like the architecture, is almost unchanged, with the exception of these improvements in the calculations of the tensor of output values.
Python code
# Определение нейронного аккумулятора (NAC) с добавлением логарифмических операций# -> Помогает при подборе более сложных операций, таких как умножение, деление и возведение в степеньdefnac_complex_single_layer(x_in, out_units, epsilon=0.000001):'''
:param x_in: Входной тензор X
:param out_units: размер выходного вектора
:param epsilon: маленькое положительное число (нужно, чтобы избежать ситуации log(0) при подсчёте результата)
:return m: Результирующий тензор заданной размерности
:return W: Матрица весов для слоя
'''
in_features = x_in.shape[1]
W_hat = tf.get_variable(shape=[in_shape, out_units],
initializer=tf.initializers.random_uniform(minval=-2, maxval=2),
trainable=True,
name="W_hat")
M_hat = tf.get_variable(shape=[in_shape, out_units],
initializer=tf.initializers.random_uniform(minval=-2, maxval=2),
trainable=True,
name="M_hat")
# Считаем W по формуле
W = tf.nn.tanh(W_hat) * tf.nn.sigmoid(M_hat)
# Логарифмируем входные данные для обучения на сложных арифметических операциях
x_modified = tf.log(tf.abs(x_in) + epsilon)
m = tf.exp(tf.matmul(x_modified, W))
return m, W
Again I remind you that you can find the full version of the code in my GitHub repository (the link is duplicated at the end of the post).
Putting it all together: neural arithmetic logic unit (NALU)
As many have already guessed, we can learn almost any arithmetic operation, combining the two models discussed above. This is the main idea of NALU , which includes a weighted combination of elementary and complex NAC , controlled through a training signal. Thus, NAC are the building blocks for the assembly of NALU , and if you understand their device, it will be easy to build NALU . If you still have questions, try again to read the explanations for both NAC models . Below is a diagram with the NALU architecture . NALU
architecture diagram with explanations
As can be seen from the figure above, both NAC blocks (purple blocks) inside NALU are interpolated (combined) through a sigmoid of the training signal (orange block). This allows (de) to activate the output of any of them, depending on the arithmetic function, the values of which we are trying to find.
As mentioned above, the elementary NAC unit is an accumulating function, which allows NALU to perform elementary linear operations (addition and subtraction), while the complex NAC unit is responsible for multiplication, division, and exponentiation. The output in NALU can be represented as a formula:
Pseudocode
Simple NAC : a = W X
Complex NAC: m = exp(W log(|X| + e))
Где W = tanh(W_hat) * sigmoid(M_hat)
# Здесь G - стандартная матрица параметров для обучения
Контролирующий сигнал: g = sigmoid(G X)
# И, наконец, выходные данные NALU# Здесь * является поэлементным умножением для матриц
NALU: y = g * a + (1 - g) * m
From the formula NALU above, we can conclude that when
the neural network will only select values for complex arithmetic operations, but not for elementary ones; and vice versa - in the case of. Thus, in general, NALU is able to study any arithmetic operation consisting of addition, subtraction, multiplication, division and exponentiation and successfully extrapolate the result beyond the limits of the initial data values.Implementing NALU in Python using Tensorflow
In the implementation of NALU, we will use elementary and complex NAC , which we have previously defined.
Python code
defnalu(x_in, out_units, epsilon=0.000001, get_weights=False):'''
:param x_in: Входной тензор X
:param out_units: размер выходного вектора
:param epsilon: маленькое положительное число (нужно, чтобы избежать ситуации log(0) при подсчёте результата)
:param get_weights: При значении True возвращает подсчитанные матрицы весов модели
:return y_out: Результирующий тензор заданной размерности
:return G: Кoнтролирующая матрица весов
:return W_simple: матрица весов для NAC1 (элементарный NAC)
:return W_complex: матрица весов для NAC2 (сложный NAC)
'''
in_features = x_in.shape[1]
# Получаем результат из элементарного NAC
a, W_simple = nac_simple_single_layer(x_in, out_units)
# Получаем результат из сложного NAC
m, W_complex = nac_complex_single_layer(x_in, out_units, epsilon=epsilon)
# Сигнал контролирующего слоя
G = tf.get_variable(shape=[in_shape, out_units],
initializer=tf.random_normal_initializer(stddev=1.0),
trainable=True,
name="Gate_weights")
g = tf.nn.sigmoid(tf.matmul(x_in, G))
y_out = g * a + (1 - g) * m
if(get_weights):
return y_out, G, W_simple, W_complex
else:
return y_out
Once again, in the code above, I again initialized the parameter matrix
using a uniform distribution, but you can use any recommended method of generating an initial approximation.Results
For me personally, the idea of NALU is a serious breakthrough in the field of AI, especially in neural networks, and it looks promising. This approach can open doors to those areas of application where standard neural networks could not cope.
The authors of the article talk about various experiments using NALU : from selecting the values of elementary arithmetic functions to counting the number of handwritten numbers in a given series of MNIST images , which allows neural networks to check computer programs!
The results make a tremendous impression and prove that NALU copes with almost any task.associated with the numerical representation, better than standard models of neural networks. I recommend that readers familiarize themselves with the results of the experiments in order to better understand how and where the NALU model can be useful.
However, it must be remembered that neither NAC nor NALU are the ideal solution for any task. They rather represent a general idea of how to create models for a particular class of arithmetic operations.
Below is a link to my GitHub repository, which contains the full implementation of the code from the article.
github.com/faizan2786/nalu_implementation
You can independently test the operation of my model on various functions by selecting hyper parameters for the neural network. Please ask questions and share your thoughts in the comments under this post, and I will do my best to answer you.
PS (from the author): this is my first ever written post, so if you have any tips, suggestions and recommendations for the future (both technical and general plan), please write to me.
PPS (from translator): if you have comments to the translation or to the text, please write me a personal message. I am particularly interested in the formulation for the learned gate signal - I am not sure that I was able to accurately translate this term.