Why do we all need SAT and all these P-NPs (part one)
SAT is already so good because it puts
Lomonosov in order ( original )
Introduction
On a habr already many articles devoted to a problem P vs. NP and the SATisfiability problem. However, most of them do not answer some of the most important questions. Why is this problem really important to us? What will happen if it is decided? Where does all this apply? And why is it necessary to have at least a general idea of what it is about?
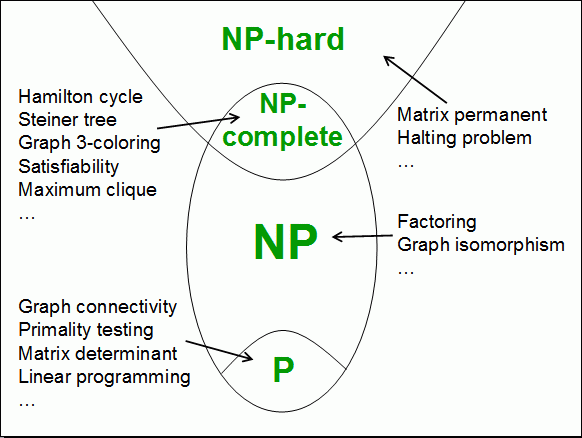
If we analyze in detail the most notable work on the Habrr on this topic [ 1 , 2 , 3 , 4 , 5 , 6 , 7], we note that on the one hand, people with knowledge in the field of computational complexity cannot learn anything fundamentally new in these articles. On the other hand, these articles are still not publicly available. The illustration from the headline clearly demonstrates the problem: those who did not understand, nothing is clear from it, and those who have already heard about it do not need it.
This article has two goals: the first is to give a general idea of the problem and answer the question, why should we know about this problem (the first part), the second is to provide material "for growth" that will be interesting to people interested in the subject, as well as may be useful for further study of the topic (second part).
Article structure
For ease of reading and navigation, we provide a brief overview of the contents of the article.
- Public Material
- Why is SAT important to us all? Applications / Interesting NP Tasks and SAT
- History of SAT and NP completeness
- Intuitive Definition of SAT, NP and P
- What happens if ... P! = NP, P = NP
- 2-SAT is polynomial: algorithm and intuition
- Task to think
- Specialized material (see in the next series)
- Formal definition. The asymmetry of the solvability problem for NP and CoNP
- 2 + p-SAT is polynomial?
- The dependence of complexity on the number of variables
- I decided P vs. NP, what should I do? Where should i write?
- Inexpressibility theorems: why the article of Romanov [ 3 ] expects reject
- About modern SAT solver'ah
- What to read?
- Task to think
Disclaimer
This work is a general educational material and is intended solely to familiarize yourself with SAT issues. Computational complexity and SAT are not the main directions of my research, but lie in a related scientific field, so if in doubt, always refer to the specified source.
Public Material
Why is SAT important to us all? Applications
In order to answer this question, you must first understand what mathematical problems affect our everyday life as an actual without our knowledge and how these problems are related to SAT.
Here is a list of the tasks that occur around us and say how they relate to the SAT.
- First of all, we mention the RSA cryptographic algorithm , which is used to ensure the safety of bank transactions, as well as to create a secure connection. The RSA algorithm can be “hacked” using SAT.
- Many recommendation systems (for example, as part of Netflix) use a Boolean matrix decomposition algorithm to recommend content. The optimal decomposition of such matrices can be found using SAT.
- The task of optimal distribution of tasks among processors can be solved using SAT. A large number of planning tasks is reduced to SAT, for example, open shop scheduling , where tasks (jobs) must go through certain stages (completed by certain workers) and it is necessary to minimize the total processing time of all tasks.
- NASA verifies its software specifications and its hardware models using model checking methods directly linked to the SAT.
- The popular k-means clustering method (k-means method) can be solved using SAT.
- Most of the interesting tasks related to graphs (for example, on social networks, the graph is the relationship of friendship between users) is the search for the largest community, where everyone is friends with everyone, the search for the longest path and many other tasks on graphs can be solved using SAT. The task from the life of the Moscow region (and not only): to compile a schedule of garbage trucks so that they go around all garbage collection points once for a minimum time. A large number of tasks in logistics comes down to the SAT task.
- Even the knapsack problem can be solved using SAT. The task is to have a satchel of a fixed size, to collect objects of the greatest value into it (knowing the sizes of all objects in advance).
- Many video games can be solved using SAT (and even Mario !) The Sudoku puzzle and, attention, Minesweeper can be solved using SAT!
- The tasks of serializing transaction history in databases can be solved using SAT.
Visualization of tasks solved using SAT (due to Bart Selman, taken from here )

What does “can be solved” mean and what does NP have to do with it?
Simply put, if we have an effective solution to the SAT problem, then we can effectively solve all these problems. What exactly is meant by efficiency depends on the specific task, but here we will assume that the working time is acceptable for the user (for scheduling a school for a semester, we can devote a couple of days to computing, and for the clustering method, we would like to get the result interactively ) And for many of the above problems the reverse is also true, if we can solve them effectively, then we can efficiently solve SAT (this is called NP-completeness - this definition is informal, but enough for a general understanding).
All these problems lie in the NP class - later we will describe the class in more detail, but now we should note that if an effective solution to the SAT problem is known, then we can effectively solve any problem in the NP class. In other words, SAT is a class representative task, it is “the most difficult” in its class and allows solving all other problems in NP.
History of SAT and NP completeness
NP completeness
The theory of computational complexity , in which languages and functions are allocated to different classes according to the amount of time and memory necessary for their calculations, was born from the theory of computability (i.e., the work of the 30s by Godel, Church and Turing) when Hartmanis, Sterns, Lewis (1965 ) proposed one of the first such classifications of functions (original works: here and here ).
The concept of NP-completeness developed independently in the 1960s and 1970s in the USSR and the USA (Edmonds, Levin, Yablonsky et al.). In 1971, Stephen Cook formulated the hypothesis of P vs. NP. The theorem that SAT is a “universal problem” for the class NP and allows solving any problem in this class (NP-completeness) was independently proved by Leonid Levin (1973) and Stephen Cook, and is called the Levin-Cook theorem . In 1982, Cook will receive a Turing Award for this work.
In 1972, Karp published Reducibility among combinatorial problems , a list showing that SAT is far from the only interesting task in NP and a huge number of tasks lie in NP and is equivalent to SAT. In 1985, Karp will receive a Turing Award for this work.
In 1974, Fagin will show that NP is closely related to classical logic, namely, that NP is equivalent to second-order existential logical structures ( Fagin's theorem ).
In 1975, Baker, Jill, and Solovey obtained the first fundamental meta-result on the unsolvability of the problem P vs. NP using regularized methods i.e. this is the first result showing that a whole class of methods cannot answer the question of equality P vs. NP (more about this is written here ).
In 1979, Gary and Johnson write " Computing Machines and Hard Problems", one of the most comprehensive sources of information on NP-completeness and a detailed catalog of tasks. Despite the fact that some theoretical results are currently considered obsolete, this is one of the most fundamental works in the field of computational complexity.
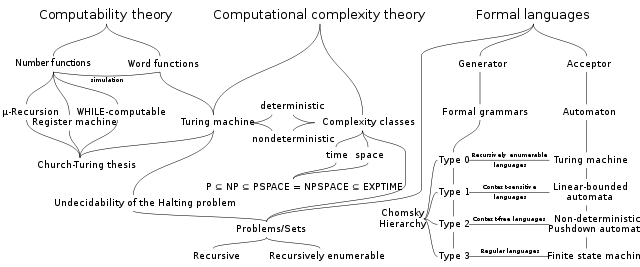
Visualization of relations between formal languages and computational theories complexity and computation theory ( from here ):
A very brief history of SAT-solvers
In the 1960s, Davis and Putman began to apply the classically deductive (to put it simply, methods for proving theorems) methods for solving SAT ( original work ).
In 1962, Davis, Putnam, Logeman, Loveland proposed a DPLL algorithm based on the search with the return and distribution of deterministic computing (unit-propagation). To put it simply, the algorithm assumed the value of some variable to be equal to the truth and calculated all the deterministic consequences of such a solution and repeated until it found a solution. This algorithm has served as the basis for many SAT solvers for decades.
In 1992, Selman, Levescu, and Mitchell proposed a local search method in a GSAT article.GSAT - means Greedy SAT, local since it decides on the value of variables based on only local information. The algorithm began with the arbitrary assignment of variable values and changed the value of the variable if it gave the greatest increase in the executed sentences. Subsequently, local search methods in a wide variety of variations were integrated into most SAT solvers - in 1999, Hegler Hus in his PhD dissertation gives an extensive study on stochastic local search and its applications (the work is available here ).
In 1996, Marques-Silva and Sakaly proposed the Conflict-Driven-Clause-Learning ( CDCL ) algorithm.), like DPLL, it makes decisions about the meaning of variables and performs deterministic calculations; on the other hand, it stores an animation graph in memory and remembers some combinations that do not lead to a solution and can effectively avoid “useless” decisions and effectively cut off the solution space containing a conflict earlier.
Since 2001, Locality Based Search SAT-solvers have begun to appear, effectively selecting subspaces for a full search based on local information, such as BerkMin (Berkley-Minsk) and many others.
Intuitive Definition of SAT, NP and P
Sat
We begin by defining what propositional logic is : a set of variables {x, y, z, ...} and a set of connectors {and, or, - (not), →}. Each variable can be either “false” or “true”. Connectors are defined as standard:
- x and y is true if and only if (for brevity we will write iff - if and only if) x is true and y is true, the classic “AND”
- x or y true iff at least one of the variables x \ y is true, classic “OR”
- -x true iff x false, classic negation
- x → y is false iff x is true and y is false - consider the following example:
“If it was raining, the grass is wet”
The statement is false if and only if the rain was (x true) and the grass is still dry (y is false )
Formula F is a syntactically correct set of variables and connectors, that is, →, and, or connect variables or other formulas, - (not) stands before a variable or formula. Example, F = (x → (y or z)) and (z → -x).
They say that the formula F is satisfiable (SAT), iff its variables can be assigned the values "true" \ "false" (we call such a function I from the English I nterpretation), so that F is true. For brevity, we write I (F) = "true."
Any propositional formula F can be reduced to the form CNF (conjunctive normal form), i.e., be represented as
F '= c 1 and c 2 and ... c n
where c iIs (x or y or z), and x, y, z are variables or their negations.
Example F = (x or -y or -z) and (-x or -y or h) and (z or h).
More details about this transformation are written here (in order for each sentence to contain no more than three variables, you will need to introduce additional variables, but these are only technical details).
In this form, when the formula has the form described above, the task is called 3-SAT, emphasizing the fact that each sentence c i contains no more than three variables or their negatives.
The statement of the 3-SAT problem is as follows:
Given: propositional formula F in the form of 3-CNF
Find :: function Iattributing the value "true" \ "false" to all variables, such that I (F) = "true"
class P
P it is PTIME - tasks solvable in polynomial time, this means that the number of algorithm steps in this class grows no more than a certain polynomial from the input data. More about various algorithms and complexity analysis in PTIME has already been written on the Habr [ 9 , 10 , 11 , 12 , 13 ].
To illustrate, here is a simple example: a bubble sort algorithm ( pseudocode from a wiki)
procedure bubbleSort( A : list of sortable items )
n = length(A)
repeat
swapped = falsefori = 1 to n-1 inclusive do
if A[i-1] > A[i] then
swap(A[i-1], A[i])
swapped = trueendifendfor
n = n - 1
until not swapped
end procedure
The input parameter is an array of numbers to sort. We are interested in the growth of time depending on the growth of the length of the array i.e. dependence of TIME time on n. Note that each iteration of the repeat loop performs no more than 3 * n steps and sets at least one element of the array to the desired location. This means that the repeat loop is executed no more than n times. This means that the number of operations (aka TIME) grows as a certain square of the length of the array (and the linear term from "n = length (A)") i.e.
TIME (n) = a * n 2 + b * n + C
In other words, the running time of the algorithm is limited by some polynomial in n, in this case we say that the running time of the algorithm does not grow faster than the square of the number of elements and write it using Big-O record
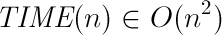
class NP
NP stands for nondeterministic polynomial time. Very often it is erroneously called non-polynomial time, a joke was born about this:
Dividing algorithms into polynomial and non-polynomial is about the same as dividing the universe into bananas and non-bananas.
In this article, we are not interested in the formal definition of NP (this will be in the specialized material), but we will consider an intuitive representation of the class NP. The very nature and internal mechanisms of the NP follow the so-called guess-and-check method. Those. the search space for the solutions is exponential (large enough to preclude brute force), and checking the solution is a simple task. You can consider NP as a class of problems in which you need to find a solution (“guess” - the guess part) among a large number of options, and then check its correctness (check part).
From the SAT point of view, the solution space is all kinds of sets of variable values, if we have k different variables in the formula, then we have 2 k possible “interpretations” of the formula, that is search space Iexponentially. However, if we “guessed” I , then we can verify the truth of the formula in polynomial time.
What happens if P! = NP
There will be nothing, only someone will receive a million dollars .
What happens if P = NP
There are two news: good and bad.
Good ones. We will very quickly solve a bunch of optimization problems, graph tasks, schedule, assemble puzzles, check various database properties, and also effectively test the performance of NASA specifications.
The bad ones. All modern cryptography is collapsing, and with it the banking system is hit. People will start writing bots for Mario.
2-SAT in P.
Consider an interesting variation of SAT, in which each clause is limited to two variables. Hereinafter, the author simplifies everything significantly to facilitate the perception of the material.
Given : F is a formula of the form c 1 and c 2 and c 3 ... and c n ,
where c i has the form (x or y) and x, y are variables or their negations, that is, x is some variable v or -v.
Find : a function I that assigns the value “true” / “false” to all variables such that I (F) = “true”
Statement : There is a polynomial algorithm P such that if function I exists, then P (F) =I , otherwise, P (F) = {}.
(*) the function I is not unique if it exists and P returns some function I (in books on the theory of algorithms and complexity, everything will be written in the formal language, but these details are not essential for perceiving the general idea of why 2-SAT is polynomial )
Sketch of evidence:
First, we transform the original formula using the following equality:
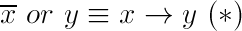
You can verify it using the truth table. The intuition behind this rule is as follows:
“If it was rain, then the grass is wet” (x → y, x - it was rain, y - grass is wet)
This means that if the grass is dry (not wet: y is false), then there was definitely no rain (x is false).
If the grass is wet, then there was either rain (x is true, in a sense, x “explains” why y is true), or there was no rain (x is false), on an intuitive level, we mean that there is another reason why y true (z - a neighbor poured grass and therefore the grass is wet).
Convert F using (*) to the form c ' 1 and c' 2 ... and c ' n where c' ihas the form (x → y), x, y are variables or their negations. As a result, F is an implication graph. An example of a similar graph below:
c 1 = If it was raining, then the grass is wet.
c 2 = If a neighbor has watered the lawn, then the grass is wet.
c 3 = If the grass is wet, weeds grow well.
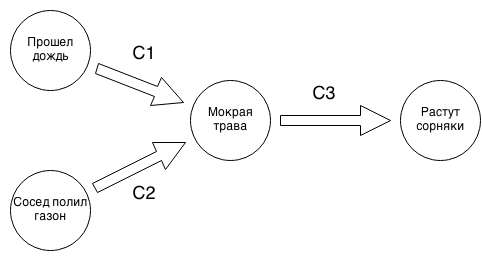
We see that if in the graph of implications leaving a certain vertex v (for example, it was raining), it is impossible to reach the peak -v (there was no rain), then the system of implications is consistent. The intuition is as follows: if we make some assumption, for example, that it was raining, we immediately conclude that the grass is wet and weeds grow (it remains only to choose whether the neighbor watered the lawn) and we do not get a contradiction, then we have part of function I, in particular, having decided that it was raining, we got the values for “grass is wet” and “weeds grow well”, we just have to decide on the meaning “neighbor poured lawn”.
How many such decisions need to be made? No more than n is the number of sentences. How many operations do you need to make when making one decision? For each solution, we need to go around the edges of the graph no more than once, that is, perform no more than n operations on one solution. This means that it is necessary to make no more than n 2 operations to find I . ■
The task "to think"
This task may require additional study and literature search.
Trivial SAT Solution
ConditionEach propositional formula F = c 1 and c 2 and c 3 and c n can be brought to a disjunctive normal form (DNF), i.e., to the form F '= c' 1 or c ' 2 ... or c' k , where c ' i has the form (x and y and z), x, y, z are variables or their negations. For example, using the consistent application of the De Morgan rules (link) and the disclosure of brackets.
For F ', there exists a trivial search algorithm for the function I. It is necessary that at least one of c' i be true. Let's write a simple pseudo-code solving the problem:
#Input: F — propositional formula in disjunctive normal form (DNF)#Output: {SAT, UNSAT}for each c in F do
if c is SAT:
return SAT
return UNSAT
For each sentence (clause) c i, the search algorithm I is also trivial, if the sentence c i does not contain some variable v and its negation at the same time, then c i is satisfiable (SAT).
Total : we get a trivial algorithm for checking the formula for feasibility
Find : where is the error?
References and Sources
The picture in the introduction is taken from the
Computational Complexity and the Anthropic Principle Scott Aaronson
Slides
Why SAT Scales: Phase Transition Phenomena & Back Doors to Complexity slides courtesy of Bart Selman Cornell University.
Slides are based on the article:
2 + P-SAT: Relation of typical-case complexity to the nature of the phase transition (Monasson, Remi; Zecchina, Riccardo; Kirkpatrick, Scott; Selman, Bart; and Troyansky, Lidror.)
Other articles can find here
More information about the history of NP can be found here:
The History and Status of the P versus NP Question by Michael Sipser
P versus NP by Elvira Mayordomo
More about SAT solvers:
SAT Solvers: A Condensed History
Understanding Modern SAT Solvers is the author of Armin Biere, perhaps the most famous SAT Solver developer in the world. Donald Knuth, who is now writing The Art of Computer Programming: Volume 4B, Pre-fascicle 6A Satisfiability, says he consults with him on many issues.
Towards a new era of SAT Solvers
Material from Habra:
[1] Why I do not believe in simple algorithms for NP-complete problems
[2] A little more about P and NP
[3] An open letter to scientists and a reference implementation of the Romanov algorithm for NP-complete 3-VYP problems
[4] Is the proof published P ≠ NP?
[5] P = NP? The most important unsolved problem of theoretical computer science.
[6] Theoretical computer science at Academic University
[7] Top-10 results in the field of algorithms for 2012
[8] It is proved that the game Super Mario is an NP-complete problem
[9] Introduction to the analysis of complexity of algorithms (part 1)
[10] Introduction to the analysis of complexity of algorithms (part 2)
[11] Introduction to the analysis of complexity of algorithms (part 3)
[12] Introduction to the analysis of complexity of algorithms (part 4)
[13] Know the complexity of algorithms
