Gray codes and enumeration tasks
This article will show a mathematical approach to compiling algorithms using the following questions and tasks as an example:
So let's get started.
A gray binary code of order n is a sequence of all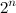 n- bit codes in which any two neighboring codes differ in exactly one bit.
n- bit codes in which any two neighboring codes differ in exactly one bit.
An example of Gray codes of order 2:
It is easy to notice that such a sequence is not the only one (it can at least be reversed). Therefore, let's look at the existence of Gray binary codes of other orders and at the same time select one kind of such sequences for further work.
The existence of Gray codes is easily proved by induction.
Base -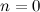 - an empty sequence.
- an empty sequence.
Transition. Let be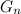 a sequence of Gray codes of order
a sequence of Gray codes of order 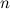 .
. 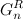 - a sequence
- a sequence 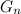 written in reverse order. Then the sequence is
written in reverse order. Then the sequence is 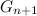 obtained by assigning zero to the left of each code in the sequence
obtained by assigning zero to the left of each code in the sequence 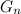 and units to the left of each code
and units to the left of each code 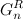 and their subsequent union, i.e.
and their subsequent union, i.e. 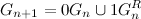 . It is easy to verify that the property of Gray codes in the sequence
. It is easy to verify that the property of Gray codes in the sequence 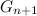 constructed in this way is not violated.
constructed in this way is not violated. 
Gray codes obtained in this way are called reflective or symmetrically reflected.. In the future, we will consider the gray reflective binary codes.
As an exercise write out symmetrically reflected Gray code order 3 of the proof given in formula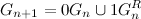 .
.
Now let's move on to the application of Gray codes to solve some problems of combinatorics.
Consider the following problem: “Given a set of n elements. It is required to deduce all of its subsets in such a way that each subsequent subset is obtained from the previous one by deleting or adding exactly one element (that is, in the order of minimal change). ”
We assume that the elements of our set are numbered from 1 to n . Then, any set of elements of the set can be associated with an n- bit binary code: if the i- th element of the set is included in the set, then the i- th bit of the code is one, otherwise zero. Thus, enumeration of all subsets is reduced to enumeration of binary codes of order n, and enumerating the subsets in the order of minimal change - to enumerating the binary Gray codes.
The idea of a recursive enumeration algorithm for Gray codes certainly follows from the proof of their existence, namely, the recurrence relation given in it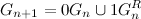 .
.
 Actually, as stated in the proof, the Gray code of order n is obtained from the Gray code of order n-1 by assigning zero to the left (this corresponds to calling the function
Actually, as stated in the proof, the Gray code of order n is obtained from the Gray code of order n-1 by assigning zero to the left (this corresponds to calling the function  and assigning it in front of it) and the reverse Gray code of order n-1 by assigning one to the left (this corresponds to calling the function
and assigning it in front of it) and the reverse Gray code of order n-1 by assigning one to the left (this corresponds to calling the function 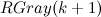 and assignment in front of him).
and assignment in front of him).
We proceed to assess the complexity of this algorithm. Obviously, the function call tree is a complete binary tree of height n . Therefore, the total number of function calls during the generation of Gray codes of order n is none other than
is a complete binary tree of height n . Therefore, the total number of function calls during the generation of Gray codes of order n is none other than  , which is equal to the number of all possible n- bit codes. Therefore, the algorithm is optimal.
, which is equal to the number of all possible n- bit codes. Therefore, the algorithm is optimal.
As an exercise, the reader is invited to analyze the following, shorter recursive search algorithm.
I would also like to say about the existence of an iterative search algorithm and other useful properties of Gray codes that are not considered in this article, and which can be learned from other sources, for example Wikipedia.
Now let's move on to the last and most interesting task.
Let's start with the statement of the problem: “A set of n elements is given. It is required to deduce all its subsets consisting of exactly k elements in such a way that each subsequent subset is obtained from the previous one by replacing exactly one element (that is, in the order of minimal change). ”
Here the idea of the algorithm from the previous problem immediately comes to mind, but we will only print those Gray codes in which exactly k units. In this case, the question arises of the correctness of this algorithm: no one guarantees us that the neighboring codes in a sequence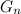 in which only binary codes with the number of units equal to k are left, are arranged in the order of minimal change - with a difference of exactly two digits - obtained from each other by replacing one element. Therefore, we proceed to a further study of the properties of symmetrically-reflected Gray codes.
in which only binary codes with the number of units equal to k are left, are arranged in the order of minimal change - with a difference of exactly two digits - obtained from each other by replacing one element. Therefore, we proceed to a further study of the properties of symmetrically-reflected Gray codes.
We introduce some notation:
 units in the sequence
units in the sequence 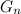 has the form
has the form 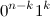 , and the last -
, and the last - 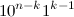 or
or  , if
, if 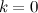 .
.
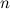 and
and  .
.
Base -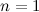 - true (it is easy to verify the above formulas for the two codes 0 and 1).
- true (it is easy to verify the above formulas for the two codes 0 and 1).
Transition. Let the formulas be true for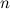 anyone
anyone  . Let us recall the formula of the proof of the existence of the Gray codes:
. Let us recall the formula of the proof of the existence of the Gray codes: 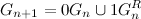 . From this we get that the first code with
. From this we get that the first code with  units in the sequence
units in the sequence 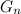 with the zero assigned to the left is the first code with
with the zero assigned to the left is the first code with  units in the sequence
units in the sequence 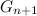 . When
. When  we get the only code with
we get the only code with  unit, for which the formula is also true. With the
unit, for which the formula is also true. With the  last code with
last code with  units in the sequence,
units in the sequence, 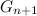 there is the first code with the
there is the first code with the 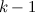 unit and the unit assigned to the left in the sequence
unit and the unit assigned to the left in the sequence 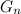 . At
. At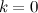 the formula is also true.
the formula is also true. 
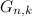 differ exactly in two digits.
differ exactly in two digits.
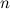 and
and  .
.
Base -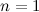 - obviously (there is only one possible code in the sequence).
- obviously (there is only one possible code in the sequence).
Transition. Let the theorem hold for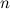 and
and  . With
. With 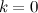 or
or  we have only one code in the sequence
we have only one code in the sequence  . When
. When  neighboring words are completely in
neighboring words are completely in 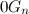 or in
or in 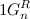 by the induction hypothesis, they differ exactly in two categories. It remains to check one pair of neighboring codes in the
by the induction hypothesis, they differ exactly in two categories. It remains to check one pair of neighboring codes in the  last code with
last code with  units in
units in 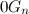 and the first code with
and the first code with  units in
units in 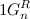 (the last with
(the last with 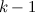 unit in
unit in 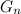 with unit assigned to the left). By the lemma, for
with unit assigned to the left). By the lemma, for  , they have the form
, they have the form 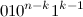 and,
and, 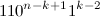 respectively, and for
respectively, and for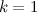 -
- 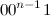 and
and  . It is easy to see that they differ in exactly two categories.
. It is easy to see that they differ in exactly two categories. 
Now we can state the remarkable consequences of the theorem.
These consequences can and should be used to write a program for recursively enumerating subsets of k elements in the order of minimal change.
 I would like to draw attention to the fact that binary code output also means filling in the remaining bits with ones or zeros, depending on the values of u and v .
I would like to draw attention to the fact that binary code output also means filling in the remaining bits with ones or zeros, depending on the values of u and v .
We proceed to estimate the complexity of the presented algorithm. Note that when deepening into recursion, the value of u always decreases. That is, we will make no more than n recesses to achieve some binary code. There are a total of such codes . We obtain the resulting asymptotic behavior
. We obtain the resulting asymptotic behavior 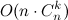 . This is a rather rough estimate, but it is in every way better
. This is a rather rough estimate, but it is in every way better  , especially whenk tending to n : the algorithm is almost linear.
, especially whenk tending to n : the algorithm is almost linear.
It is easy to notice that the call tree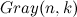 will be binary, but not complete. Let us draw a parallel of complexity assessment in terms of trees: each leaf corresponds to receiving some binary code, and the distance to the leaf in the tree does not exceed n . The estimate
will be binary, but not complete. Let us draw a parallel of complexity assessment in terms of trees: each leaf corresponds to receiving some binary code, and the distance to the leaf in the tree does not exceed n . The estimate 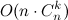 tells us that we simply summed up the upper estimate of the lengths - n - of all the paths to the sheets. But after all, many of these paths have a length less than n , and even more paths intersect with each other. This should lead us to the idea that the asymptotic behavior of the presented algorithm is actually much better.
tells us that we simply summed up the upper estimate of the lengths - n - of all the paths to the sheets. But after all, many of these paths have a length less than n , and even more paths intersect with each other. This should lead us to the idea that the asymptotic behavior of the presented algorithm is actually much better.
An exact estimate of the asymptotics is far from a trivial fact, which can be found in the book by E. Reingold, J. Nievergelt and N. Deo “Combinatorial Algorithms. Theory and practice ”, or try to prove it yourself.
On this I would like to end the article. Thank you and see you soon.
- Binary codes of Gray. Their existence. Enumeration of subsets of a given set in the order of minimal change.
- Existence and implementation of enumeration of subsets of k elements in the order of minimal change.
So let's get started.
Gray Binary Code
A gray binary code of order n is a sequence of all
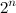 n- bit codes in which any two neighboring codes differ in exactly one bit.
n- bit codes in which any two neighboring codes differ in exactly one bit. An example of Gray codes of order 2:
- 00
- 01
- eleven
- 10
It is easy to notice that such a sequence is not the only one (it can at least be reversed). Therefore, let's look at the existence of Gray binary codes of other orders and at the same time select one kind of such sequences for further work.
Existence
The existence of Gray codes is easily proved by induction.
Base -
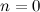 - an empty sequence.
- an empty sequence. Transition. Let be
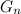 a sequence of Gray codes of order
a sequence of Gray codes of order 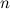 .
. 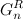 - a sequence
- a sequence 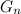 written in reverse order. Then the sequence is
written in reverse order. Then the sequence is 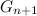 obtained by assigning zero to the left of each code in the sequence
obtained by assigning zero to the left of each code in the sequence 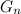 and units to the left of each code
and units to the left of each code 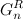 and their subsequent union, i.e.
and their subsequent union, i.e. 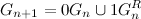 . It is easy to verify that the property of Gray codes in the sequence
. It is easy to verify that the property of Gray codes in the sequence 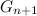 constructed in this way is not violated.
constructed in this way is not violated. 
Gray codes obtained in this way are called reflective or symmetrically reflected.. In the future, we will consider the gray reflective binary codes.
As an exercise write out symmetrically reflected Gray code order 3 of the proof given in formula
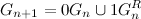 .
. Now let's move on to the application of Gray codes to solve some problems of combinatorics.
Enumeration of subsets of a given set in the order of minimal change
Consider the following problem: “Given a set of n elements. It is required to deduce all of its subsets in such a way that each subsequent subset is obtained from the previous one by deleting or adding exactly one element (that is, in the order of minimal change). ”
We assume that the elements of our set are numbered from 1 to n . Then, any set of elements of the set can be associated with an n- bit binary code: if the i- th element of the set is included in the set, then the i- th bit of the code is one, otherwise zero. Thus, enumeration of all subsets is reduced to enumeration of binary codes of order n, and enumerating the subsets in the order of minimal change - to enumerating the binary Gray codes.
The idea of a recursive enumeration algorithm for Gray codes certainly follows from the proof of their existence, namely, the recurrence relation given in it
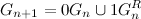 .
.  Actually, as stated in the proof, the Gray code of order n is obtained from the Gray code of order n-1 by assigning zero to the left (this corresponds to calling the function
Actually, as stated in the proof, the Gray code of order n is obtained from the Gray code of order n-1 by assigning zero to the left (this corresponds to calling the function  and assigning it in front of it) and the reverse Gray code of order n-1 by assigning one to the left (this corresponds to calling the function
and assigning it in front of it) and the reverse Gray code of order n-1 by assigning one to the left (this corresponds to calling the function 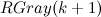 and assignment in front of him).
and assignment in front of him). We proceed to assess the complexity of this algorithm. Obviously, the function call tree
 is a complete binary tree of height n . Therefore, the total number of function calls during the generation of Gray codes of order n is none other than
is a complete binary tree of height n . Therefore, the total number of function calls during the generation of Gray codes of order n is none other than  , which is equal to the number of all possible n- bit codes. Therefore, the algorithm is optimal.
, which is equal to the number of all possible n- bit codes. Therefore, the algorithm is optimal. As an exercise, the reader is invited to analyze the following, shorter recursive search algorithm.
Example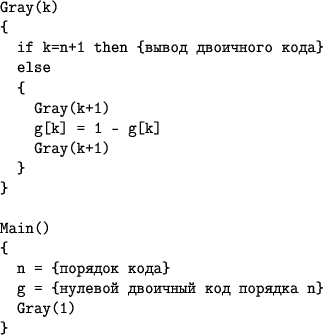

I would also like to say about the existence of an iterative search algorithm and other useful properties of Gray codes that are not considered in this article, and which can be learned from other sources, for example Wikipedia.
Now let's move on to the last and most interesting task.
Enumeration of subsets of k elements in the order of minimal change.
Let's start with the statement of the problem: “A set of n elements is given. It is required to deduce all its subsets consisting of exactly k elements in such a way that each subsequent subset is obtained from the previous one by replacing exactly one element (that is, in the order of minimal change). ”
Here the idea of the algorithm from the previous problem immediately comes to mind, but we will only print those Gray codes in which exactly k units. In this case, the question arises of the correctness of this algorithm: no one guarantees us that the neighboring codes in a sequence
 in which only binary codes with the number of units equal to k are left, are arranged in the order of minimal change - with a difference of exactly two digits - obtained from each other by replacing one element. Therefore, we proceed to a further study of the properties of symmetrically-reflected Gray codes.
in which only binary codes with the number of units equal to k are left, are arranged in the order of minimal change - with a difference of exactly two digits - obtained from each other by replacing one element. Therefore, we proceed to a further study of the properties of symmetrically-reflected Gray codes. We introduce some notation:
 Is the string obtained by concatenating the character x ( m times) and concatenating the character y ( k times). Example
Is the string obtained by concatenating the character x ( m times) and concatenating the character y ( k times). Example 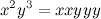 .
.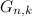 - the sequence of all n- bit codes with k units, in which the codes are in the order in which they are located in the sequence
- the sequence of all n- bit codes with k units, in which the codes are in the order in which they are located in the sequence 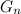 .
.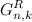 - the sequence of all n- bit codes with k units, in which the codes are in the order in which they are located in the sequence
- the sequence of all n- bit codes with k units, in which the codes are in the order in which they are located in the sequence 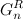 .
.
Lemma
The first binary code with units in the sequence
units in the sequence 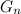 has the form
has the form 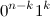 , and the last -
, and the last - 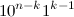 or
or  , if
, if 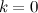 .
.Evidence
We prove by induction on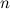 and
and  .
. Base -
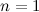 - true (it is easy to verify the above formulas for the two codes 0 and 1).
- true (it is easy to verify the above formulas for the two codes 0 and 1). Transition. Let the formulas be true for
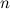 anyone
anyone  . Let us recall the formula of the proof of the existence of the Gray codes:
. Let us recall the formula of the proof of the existence of the Gray codes: 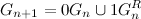 . From this we get that the first code with
. From this we get that the first code with  units in the sequence
units in the sequence 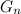 with the zero assigned to the left is the first code with
with the zero assigned to the left is the first code with  units in the sequence
units in the sequence 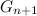 . When
. When  we get the only code with
we get the only code with  unit, for which the formula is also true. With the
unit, for which the formula is also true. With the  last code with
last code with  units in the sequence,
units in the sequence, 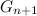 there is the first code with the
there is the first code with the 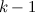 unit and the unit assigned to the left in the sequence
unit and the unit assigned to the left in the sequence 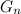 . At
. At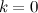 the formula is also true.
the formula is also true. 
Theorem
The adjacent binary codes in the sequence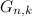 differ exactly in two digits.
differ exactly in two digits.Evidence
We will also prove by induction on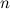 and
and  .
. Base -
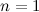 - obviously (there is only one possible code in the sequence).
- obviously (there is only one possible code in the sequence). Transition. Let the theorem hold for
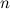 and
and  . With
. With 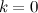 or
or  we have only one code in the sequence
we have only one code in the sequence  . When
. When  neighboring words are completely in
neighboring words are completely in 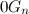 or in
or in 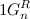 by the induction hypothesis, they differ exactly in two categories. It remains to check one pair of neighboring codes in the
by the induction hypothesis, they differ exactly in two categories. It remains to check one pair of neighboring codes in the  last code with
last code with  units in
units in 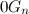 and the first code with
and the first code with  units in
units in 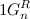 (the last with
(the last with 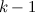 unit in
unit in 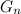 with unit assigned to the left). By the lemma, for
with unit assigned to the left). By the lemma, for  , they have the form
, they have the form 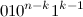 and,
and, 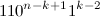 respectively, and for
respectively, and for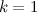 -
- 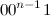 and
and  . It is easy to see that they differ in exactly two categories.
. It is easy to see that they differ in exactly two categories. 
Now we can state the remarkable consequences of the theorem.
- The naive algorithm proposed earlier is correct, that is, if
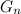 only binary codes in which exactly k units are left in the sequence , then they will be arranged in the order of minimal change (each following is obtained from the previous one by replacing one element).
only binary codes in which exactly k units are left in the sequence , then they will be arranged in the order of minimal change (each following is obtained from the previous one by replacing one element). - The sequence
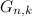 is given by the following recurrence relation
is given by the following recurrence relation 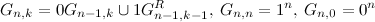 . This can be verified by induction.
. This can be verified by induction. - The sequence
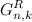 is given by the following recurrence relation
is given by the following recurrence relation  . Also verified by induction.
. Also verified by induction.
These consequences can and should be used to write a program for recursively enumerating subsets of k elements in the order of minimal change.
 I would like to draw attention to the fact that binary code output also means filling in the remaining bits with ones or zeros, depending on the values of u and v .
I would like to draw attention to the fact that binary code output also means filling in the remaining bits with ones or zeros, depending on the values of u and v . We proceed to estimate the complexity of the presented algorithm. Note that when deepening into recursion, the value of u always decreases. That is, we will make no more than n recesses to achieve some binary code. There are a total of such codes
 . We obtain the resulting asymptotic behavior
. We obtain the resulting asymptotic behavior 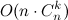 . This is a rather rough estimate, but it is in every way better
. This is a rather rough estimate, but it is in every way better  , especially whenk tending to n : the algorithm is almost linear.
, especially whenk tending to n : the algorithm is almost linear. It is easy to notice that the call tree
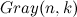 will be binary, but not complete. Let us draw a parallel of complexity assessment in terms of trees: each leaf corresponds to receiving some binary code, and the distance to the leaf in the tree does not exceed n . The estimate
will be binary, but not complete. Let us draw a parallel of complexity assessment in terms of trees: each leaf corresponds to receiving some binary code, and the distance to the leaf in the tree does not exceed n . The estimate 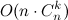 tells us that we simply summed up the upper estimate of the lengths - n - of all the paths to the sheets. But after all, many of these paths have a length less than n , and even more paths intersect with each other. This should lead us to the idea that the asymptotic behavior of the presented algorithm is actually much better.
tells us that we simply summed up the upper estimate of the lengths - n - of all the paths to the sheets. But after all, many of these paths have a length less than n , and even more paths intersect with each other. This should lead us to the idea that the asymptotic behavior of the presented algorithm is actually much better.An exact estimate of the asymptotics is far from a trivial fact, which can be found in the book by E. Reingold, J. Nievergelt and N. Deo “Combinatorial Algorithms. Theory and practice ”, or try to prove it yourself.
On this I would like to end the article. Thank you and see you soon.
