Sun 24x7: Calculation EROEI
Over the past 10 years, solar energy has rapidly shifted from “toys” to the most serious projects, and the continuation of the curve of this take-off promises total domination of this type of generation in the future. Or not? In the attempts to predict, there are a lot of copies broken and there are two main complaints: the sun does not shine through the clouds at night (ie, the source is variable) and the high energy intensity of the production of solar cells, and this energy does not return during the latter. ( EROEI <1)
Technically, the first problem with variability is solved - you just need to build more solar panels and a battery of sufficient capacity. However, this approach clearly exacerbates the problem with EROEI and the cost of electricity. Cost can be seen in reviews Lazard, but I did not see any attempts to calculate EROEI for a solar power station with a battery. Therefore, I decided to calculate it myself, and got a rather unexpected result, which is at the end.
To evaluate, let's calculate a power station with a lithium-ion battery located in Yuma, Arizona, USA. Why in Arizona? This is a very good place for solar power plants (one of the best in the world) and there is a lot of information on it. If here EROEI turns out to be less than one, then it will mean big problems for the sun as the basic source of electricity (for today). If EROEI is higher, then, taking into account the analysis we are going to make, it will be possible to easily apply the calculation to any place in the world.

In Yuma, by the way, there is a rather large Agua Caliente Solar Project SES with a capacity of 250 megawatts, but not 24x7. The solar cells of this station are made using thin-film technology from CdTe semiconductor, which differs from silicon by much better energy costs per kilowatt of battery power, but loses in cost.
The lithium-ionic is chosen because of the obvious universality of such a solution: if the hydroaccumulator requires a suitable landscape, then electrochemical can be put practically anywhere. In fact, lithium-ion batteries actually have a couple of advantages: the ability to play on peak demand (since the inverters of this system can switch from charge to discharge almost instantly) and the prospects for cheapness (over the past 10 years, the price is 1 kilowatt * lithium-ion cell hours dropped from $ 1,000 to $ 130).
So let's say we need a power plant that produces 300 MW of 365 days a year, 24 hours a day., which corresponds to the production of 7200 MWh every day and 2.6 TWh of electric power per year - about 35% of a gigawatt power unit of nuclear power plants. We will place our SES “24x7” in the town of Yuma, Arizona with coordinates of 32.69265 ° north latitude and 114.62769 ° west longitude.
Exactly from this point (as the TZ ended and the implementation began) difficulties begin: the fact is that the station can be optimized by EROEI is pretty cool, for example, if you ask not a one-day battery, but a two-day battery, which in turn will change the optimum slope of the batteries, etc. P. etc. In order to find the best of this, and not accidental, it is necessary to make a normal engineering study at this stage. Unfortunately, I do not have much time, so the EROEI numbers will not end up being the most optimal, but that is what it is. Anyone can then write in the comments and get a spread with hourly modeling, in which I considered the station, and improve the result myself.
For example, due to the wild oversize, our station does not feel any seasonal fluctuations, which reach 30 degrees for the latitude of approximately + -20% of the average value, and it is the seasonal fluctuations that will determine the future of solar energy.
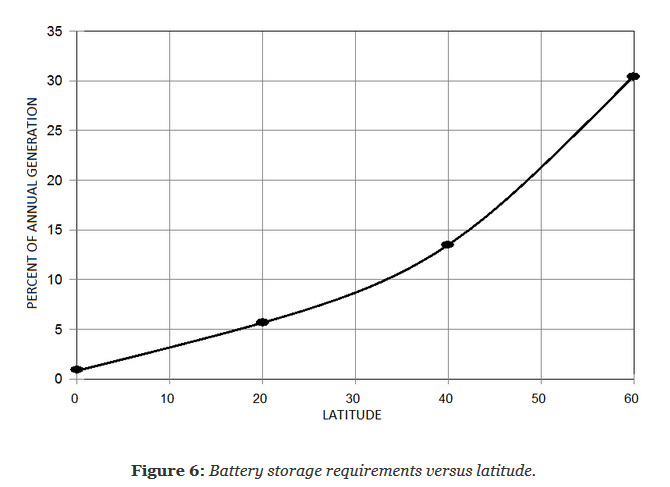
The curve in the graph shows the volume of the battery as a percentage of the annual generation, which is needed to smooth out the seasonal fluctuations, if the SATs are made “in size”. For our 2.6 TWh and 32 degrees north latitude, a battery of 234 GWh is needed — an insane amount.
Let's start the calculation with the simplest - “energy income” of our power plant. As we shall see, its electrochemical battery will be quite large and will operate mainly with a discharge depth of less than 50%, which ensures a lifetime (for LiFePo) no worse than 10,000 cycles before degradation of 20% of capacity. 10k cycles is 27 years old, let's restrict ourselves to 25 years before the station is completely renewed, and the discarded balance will compensate us for the unreadable degradation of panels and batteries.
So, for 25 years, the station should deliver 65.7 TWh according to the TOR - this is our numerator in the calculation of EROEI. But how much will a joule cost to build such a station? Let's first see the necessary set of equipment.
To determine, in the roughest form, how much we need a SAT and a battery, I will use the calculationNREL Pwatts calculator. It is based on the table of sun insolation values for our point, taken from the “ standard meteorological year ” - a database of meteorological parameters for the United States with harmonized values. Using this calculator, you can get the hourly values of power generation, taking into account the angles of incidence of the sun, ambient light, panel temperature and conversion losses, which was done as a basis for further calculations.
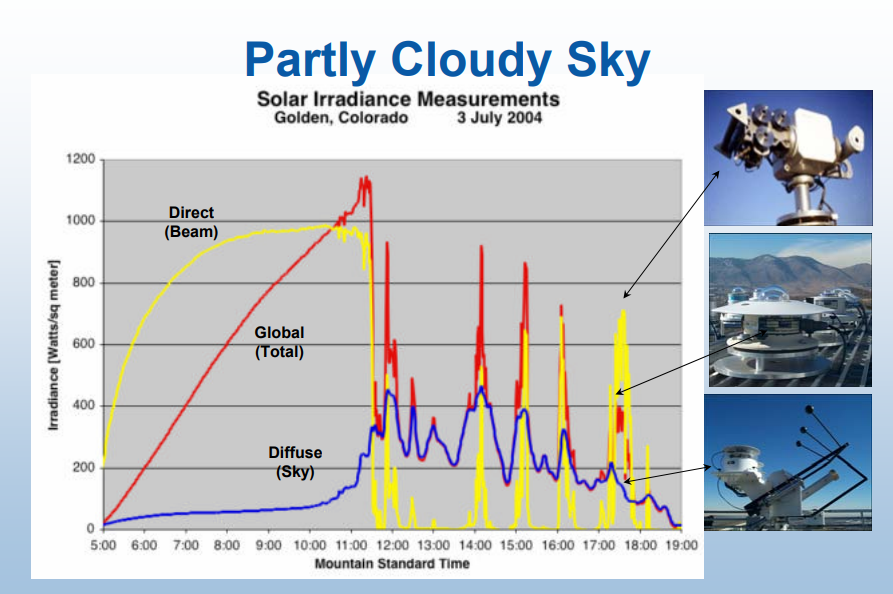
The “Standard Meteorological Year” is a very powerful database, with measurements of such subtleties as the solar direct (yellow curve on the graph) and indirect (blue) illumination, which allows you to accurately estimate the output of the simulated SS on cloudy days.
Now, the data obtained for a single-kilowatt SES need to be somehow optimized. You can change the ratio between the volume of solar cells and batteries (the more solar cells, the less we need to store energy in order to survive the dark days without turning off) and also the angle of installation of solar cells.
For our solar power plant, the defining moments of EROEI will be cloudy winter days, for example, December 27-28, in the standard meteorological year - for these two days, the station's power factor will amount to a disastrous 3.4% and fully determines its oversize, which will result in 95% of the rest days
In principle, it would be more correct to take and change the TOR for a more optimal one - for example, “300 megawatts 90% of the time of year”, then the station could be several times smaller, however, we will consider this option next time, but for now - hardcore.
So, the installation angle of solar panels needs to be optimized not for maximum energy performance during the year, but for maximum performance during a couple of the worst periods - it turns out 41 degrees, and not the most optimal 32 (the difference, however, is only 5% in annual output).
The ratio of the volume of the battery and solar panels is calculated a little more difficult - as the optimum energy. Taking into account the fact that 1 electric kilowatt of a solar power station costs ~ 14 GJ ( 2016 study), and one electric kilowatt * hour of lithium-ion batteries is about 1.6 GJ ( 2012 study ).
Hence the optimization rule - we increase the battery until we reach a situation where an increase of 8.75 kWh no longer leads to a drop in the power of solar panels by at least 1 kilowatt.
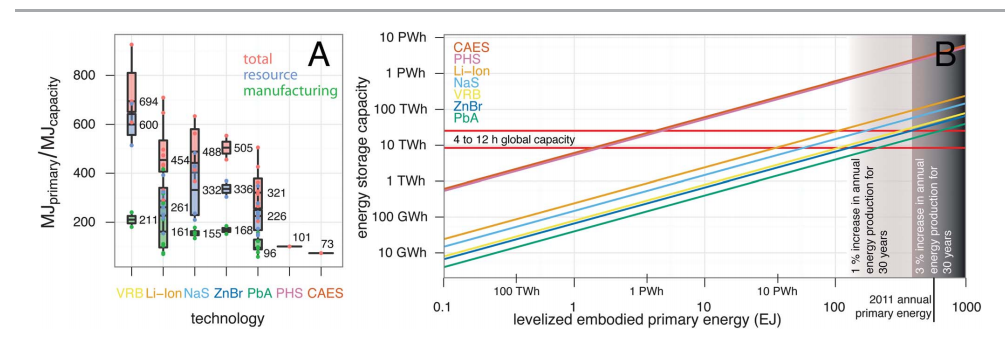
An interesting graph from the article on the energy cost of batteries. In particular, the most “energy-cheap” are hydroaccumulator (PHS) and compressed air (CAES) - according to the latter, it’s not very easy, because it uses natural gas for energy recovery. The right panel shows the “energy value” of a 4–12 hour global repository.
Busting various combinations of SB and battery size in the Pwatts issue gave me such optimal values - 2.25 GW of SB and 20 GW * h of battery. At the same time, the station will issue 300 megawatts for the entire 8760 hours of the year, and the battery charge will only once fall to 2% of the full, and will generally fluctuate between 50 and 100%. The utilization rate of the installed capacity (ICUM) of the generating part is bad - about 0.08 and a significant improvement in its network would be the reception of daytime peaks at least at the level of 2 gigawatts, then the total capacity factor would be about 0.2, which is much closer to the actual SES of the type from the image above.
It would be even better to limit the work of the station to 330 in the sunniest days of the year - then the size of the SB part could be reduced to 1.4 GW and the battery to 7 GWh. Yes, the changeable renewable energy sources have problems of the last percent in the power system - the difference between 80% share and 100% is enormous from the point of view of investments.
Well, we consider EROEI. At 2.25 GW of the sun and 20 GWh of lithium, we need 64.1 petajoules (14 * 10 9 J * 2.25 * 10 6 kW + 1.634 * 10 9 J * 20 * 10 6 kWh) or 17.82 TWh, and EROEI turns out to be equal to 3.8. People who are aware of the discourse around the sun and EROEI this number is surprising - much more than expectations. Yes, the result is ambiguous - on the one hand, it is easy to increase it several times by accepting solar generation peaks and reducing the station’s working time for the year to at least 90%, on the other hand, it is Arizona, one of the best points on the planet for solar power plants.
And most importantly, such a project is not yet feasible from a financial point of view. Even optimized 1.4 GW + 7 GWTH will cost no less than $ 4 billion, which would cost the electricity from this object at $ 140 per MW * h - too expensive. “Solar & Storage”, which appear in reality, are still trying to limit themselves to a much smaller battery, providing mainly the passage of the evening peak + the replacement of pickers, i.e. gas turbine power plants, quickly launched in case of occurrence of unplanned consumption peaks: it is clear that the cost of electricity from pickers is very high and this can be earned.
Summing up, I would like to note that the calculation carried out shows that at least physics does not prohibit the spread of solar storage power plants, at least in places with good insolation. However, there are quite a few such places on the planet, so in the next 10 years, apparently, such power plants will be massively built.
Technically, the first problem with variability is solved - you just need to build more solar panels and a battery of sufficient capacity. However, this approach clearly exacerbates the problem with EROEI and the cost of electricity. Cost can be seen in reviews Lazard, but I did not see any attempts to calculate EROEI for a solar power station with a battery. Therefore, I decided to calculate it myself, and got a rather unexpected result, which is at the end.
To evaluate, let's calculate a power station with a lithium-ion battery located in Yuma, Arizona, USA. Why in Arizona? This is a very good place for solar power plants (one of the best in the world) and there is a lot of information on it. If here EROEI turns out to be less than one, then it will mean big problems for the sun as the basic source of electricity (for today). If EROEI is higher, then, taking into account the analysis we are going to make, it will be possible to easily apply the calculation to any place in the world.

In Yuma, by the way, there is a rather large Agua Caliente Solar Project SES with a capacity of 250 megawatts, but not 24x7. The solar cells of this station are made using thin-film technology from CdTe semiconductor, which differs from silicon by much better energy costs per kilowatt of battery power, but loses in cost.
The lithium-ionic is chosen because of the obvious universality of such a solution: if the hydroaccumulator requires a suitable landscape, then electrochemical can be put practically anywhere. In fact, lithium-ion batteries actually have a couple of advantages: the ability to play on peak demand (since the inverters of this system can switch from charge to discharge almost instantly) and the prospects for cheapness (over the past 10 years, the price is 1 kilowatt * lithium-ion cell hours dropped from $ 1,000 to $ 130).
So let's say we need a power plant that produces 300 MW of 365 days a year, 24 hours a day., which corresponds to the production of 7200 MWh every day and 2.6 TWh of electric power per year - about 35% of a gigawatt power unit of nuclear power plants. We will place our SES “24x7” in the town of Yuma, Arizona with coordinates of 32.69265 ° north latitude and 114.62769 ° west longitude.
Exactly from this point (as the TZ ended and the implementation began) difficulties begin: the fact is that the station can be optimized by EROEI is pretty cool, for example, if you ask not a one-day battery, but a two-day battery, which in turn will change the optimum slope of the batteries, etc. P. etc. In order to find the best of this, and not accidental, it is necessary to make a normal engineering study at this stage. Unfortunately, I do not have much time, so the EROEI numbers will not end up being the most optimal, but that is what it is. Anyone can then write in the comments and get a spread with hourly modeling, in which I considered the station, and improve the result myself.
For example, due to the wild oversize, our station does not feel any seasonal fluctuations, which reach 30 degrees for the latitude of approximately + -20% of the average value, and it is the seasonal fluctuations that will determine the future of solar energy.

The curve in the graph shows the volume of the battery as a percentage of the annual generation, which is needed to smooth out the seasonal fluctuations, if the SATs are made “in size”. For our 2.6 TWh and 32 degrees north latitude, a battery of 234 GWh is needed — an insane amount.
Let's start the calculation with the simplest - “energy income” of our power plant. As we shall see, its electrochemical battery will be quite large and will operate mainly with a discharge depth of less than 50%, which ensures a lifetime (for LiFePo) no worse than 10,000 cycles before degradation of 20% of capacity. 10k cycles is 27 years old, let's restrict ourselves to 25 years before the station is completely renewed, and the discarded balance will compensate us for the unreadable degradation of panels and batteries.
So, for 25 years, the station should deliver 65.7 TWh according to the TOR - this is our numerator in the calculation of EROEI. But how much will a joule cost to build such a station? Let's first see the necessary set of equipment.
To determine, in the roughest form, how much we need a SAT and a battery, I will use the calculationNREL Pwatts calculator. It is based on the table of sun insolation values for our point, taken from the “ standard meteorological year ” - a database of meteorological parameters for the United States with harmonized values. Using this calculator, you can get the hourly values of power generation, taking into account the angles of incidence of the sun, ambient light, panel temperature and conversion losses, which was done as a basis for further calculations.

The “Standard Meteorological Year” is a very powerful database, with measurements of such subtleties as the solar direct (yellow curve on the graph) and indirect (blue) illumination, which allows you to accurately estimate the output of the simulated SS on cloudy days.
Now, the data obtained for a single-kilowatt SES need to be somehow optimized. You can change the ratio between the volume of solar cells and batteries (the more solar cells, the less we need to store energy in order to survive the dark days without turning off) and also the angle of installation of solar cells.
For our solar power plant, the defining moments of EROEI will be cloudy winter days, for example, December 27-28, in the standard meteorological year - for these two days, the station's power factor will amount to a disastrous 3.4% and fully determines its oversize, which will result in 95% of the rest days
In principle, it would be more correct to take and change the TOR for a more optimal one - for example, “300 megawatts 90% of the time of year”, then the station could be several times smaller, however, we will consider this option next time, but for now - hardcore.
So, the installation angle of solar panels needs to be optimized not for maximum energy performance during the year, but for maximum performance during a couple of the worst periods - it turns out 41 degrees, and not the most optimal 32 (the difference, however, is only 5% in annual output).
The ratio of the volume of the battery and solar panels is calculated a little more difficult - as the optimum energy. Taking into account the fact that 1 electric kilowatt of a solar power station costs ~ 14 GJ ( 2016 study), and one electric kilowatt * hour of lithium-ion batteries is about 1.6 GJ ( 2012 study ).
Hence the optimization rule - we increase the battery until we reach a situation where an increase of 8.75 kWh no longer leads to a drop in the power of solar panels by at least 1 kilowatt.

An interesting graph from the article on the energy cost of batteries. In particular, the most “energy-cheap” are hydroaccumulator (PHS) and compressed air (CAES) - according to the latter, it’s not very easy, because it uses natural gas for energy recovery. The right panel shows the “energy value” of a 4–12 hour global repository.
Busting various combinations of SB and battery size in the Pwatts issue gave me such optimal values - 2.25 GW of SB and 20 GW * h of battery. At the same time, the station will issue 300 megawatts for the entire 8760 hours of the year, and the battery charge will only once fall to 2% of the full, and will generally fluctuate between 50 and 100%. The utilization rate of the installed capacity (ICUM) of the generating part is bad - about 0.08 and a significant improvement in its network would be the reception of daytime peaks at least at the level of 2 gigawatts, then the total capacity factor would be about 0.2, which is much closer to the actual SES of the type from the image above.
It would be even better to limit the work of the station to 330 in the sunniest days of the year - then the size of the SB part could be reduced to 1.4 GW and the battery to 7 GWh. Yes, the changeable renewable energy sources have problems of the last percent in the power system - the difference between 80% share and 100% is enormous from the point of view of investments.
Well, we consider EROEI. At 2.25 GW of the sun and 20 GWh of lithium, we need 64.1 petajoules (14 * 10 9 J * 2.25 * 10 6 kW + 1.634 * 10 9 J * 20 * 10 6 kWh) or 17.82 TWh, and EROEI turns out to be equal to 3.8. People who are aware of the discourse around the sun and EROEI this number is surprising - much more than expectations. Yes, the result is ambiguous - on the one hand, it is easy to increase it several times by accepting solar generation peaks and reducing the station’s working time for the year to at least 90%, on the other hand, it is Arizona, one of the best points on the planet for solar power plants.
And most importantly, such a project is not yet feasible from a financial point of view. Even optimized 1.4 GW + 7 GWTH will cost no less than $ 4 billion, which would cost the electricity from this object at $ 140 per MW * h - too expensive. “Solar & Storage”, which appear in reality, are still trying to limit themselves to a much smaller battery, providing mainly the passage of the evening peak + the replacement of pickers, i.e. gas turbine power plants, quickly launched in case of occurrence of unplanned consumption peaks: it is clear that the cost of electricity from pickers is very high and this can be earned.
Summing up, I would like to note that the calculation carried out shows that at least physics does not prohibit the spread of solar storage power plants, at least in places with good insolation. However, there are quite a few such places on the planet, so in the next 10 years, apparently, such power plants will be massively built.
