Today I will bring to your attention a nice algorithm, which, although it was just recently invented (11 years ago), the counting device with a three-thousand-year history served as a “prototype”.

The authors

Sorting presented in 2002, three mathematicians from the University of Auckland, in New Zealand: Joshua J. Arulanandam. (Joshua J. Arulanandham), Christian S. Kaludiya (Cristian S. Calude) and Michael J. Dineen. (By Michael J. Dinneen). The fields of activity of scientists are discrete mathematics, number theory, quantum computing, information theory, combinatorial algorithms.

I do not know which of the three of them belongs to the original idea. Perhaps Kalud, who, among other things, teaches the history of computational mathematics. Everyone knows, the ancestor of accounts in Europe is the abacuswho migrated from Babylon to Egypt, from there to Greece, from it to Rome, from which throughout Europe. The appearance and function of the ancient "calculator" is so reminiscent of the behavior of this 'simple' sorting that it is sometimes called - " Abakovaya sort » (Abacus sort).

Algorithm

Suppose you want to sort a set of natural numbers . Under each other, lay out each number in the form of a horizontal row of the corresponding number of balls. Now let’s look at all these groups of balls not horizontally, but vertically . Push the balls all the way down. Again, switch to the horizontal and count the beads in each row. Got an initial set of numbers, only ordered.

Implementation

Bead sort in 30+ programming languages ​​can be found here . Although visually the algorithm looks nowhere simpler, from the point of view of software implementation, this is a very nontrivial sort.

Degenerate case

This is a reverse-ordered array . The maximum possible number of balls will have to collapse from the highest points.

Limited applicability

The method is primarily applicable to natural numbers .

You can sort integers, but it's more complicated - negative numbers have to be processed separately from positive ones.

Nothing prevents sorting and fractional numbers, if you first bring them to integers (for example, multiply everything by 10 ^k , sort, and then divide by 10 ^k ).

Well, of course, even rows can be sorted in this way, if each of them is represented as a positive integer. But why?

Time complexity

There are already 4 of them in sorting, depending on the context in which to consider the algorithm.

O (1)

Abstract case, spherical bead sort in a vacuum. If we imagine that all the moving balls are simultaneously shifted and fall into place. This is an unrealizable complexity for this sorting - neither in the theory of algorithms, nor in practice.

O (√n)

An estimate for a physical model where beads glide down well-oiled knitting needles. The free fall time is proportional to the square root of the maximum height, which in turn is a multiple of n .

O (n)

Balls that have not yet reached their places, together move one position down in one iteration. It is appropriate to talk about this complexity in the case of physical devices that implement this sorting method, analog or digital hardware implementations.

O (S)

S is the sum of the elements of the array. Each ball moves individually, and do not roll groups of balls at the same time. Adequate complexity assessment for implementation in programming languages.

Memory difficulty

It leaves much to be desired. Bead sort is a record holder for extravagance - the cost of additional memory is many times higher than the cost of storing the array itself and averages O (n ² ) .

Physics

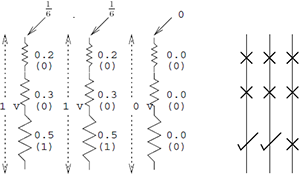
The presence or absence of balls can be interpreted as analog voltage passing through a series of electrical resistors. The rods along which the balls move are analogues of electrical resistors , the voltage in which increases from top to bottom.

Do not kick for the tongue-tied use of electrical engineering terms, I had a triple with plus four and minus in my physics school .

I send experts of electrostatics for details in this pdf-document .

In fact

Bead sort is a type of counting sort . The number of balls in each vertical track is the number of elements in the array equal to or greater than the serial number of the vertical.

Algorithm Characteristics

Title	Bead sorting; Abacus sort
The authors	Joshua J. Arulanandam, Christian S. Calud, Michael J. Dinin
Year of publication	2002
Class	Distribution Sort
Sustainability	Sustainable
Comparisons	No comparisons
Time complexity	O (1)	O (√n)	O (n)	O (S)
Memory difficulty	O (n 2 )

References

Bead sorting on the University of Auckland website
Authors documentation on the algorithm, pdf
Implementation on various PL
Bead sort in the English Wikipedia

Authors home pages:

Joshua J. Arulanandham
Christian S. Kalud
Michael J. Dinin