As I taught AI to play Tetris for NES. Part 1: game code analysis
- Transfer
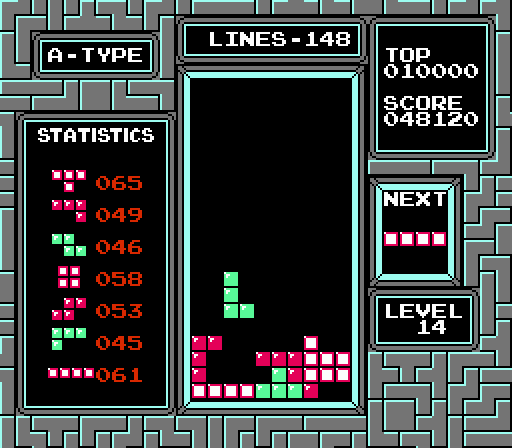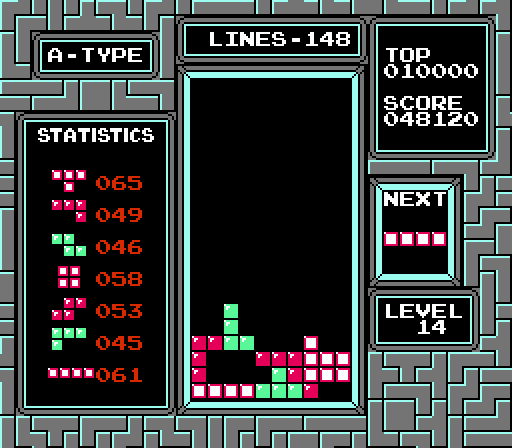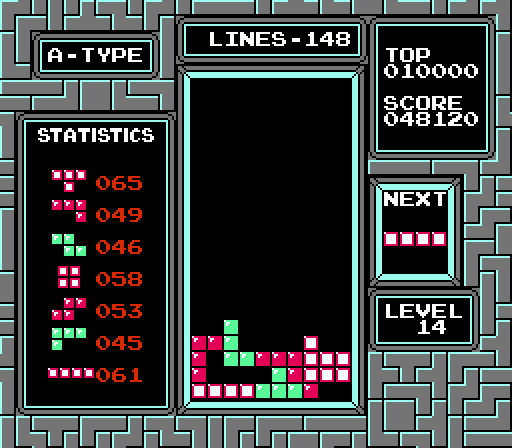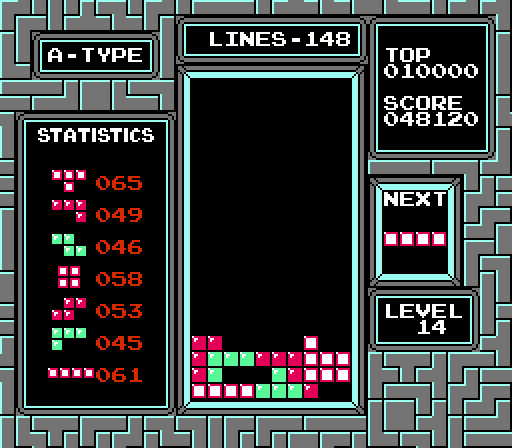
In this article, I explore the deceptively simple mechanics of Nintendo Tetris, and in the second part I will explain how I created the AI that exploits these mechanics.
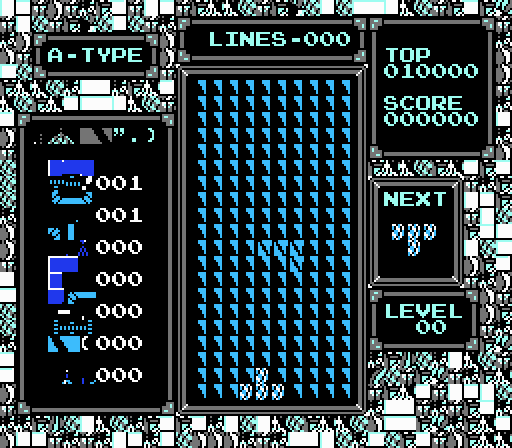
For those who lack the perseverance, patience and time needed to master Nintendo Tetris, I created an AI capable of playing on my own. You can finally get to level 30 and beyond. You will see how to get the maximum points and watch the endless changes in the counters of rows, levels and statistics. Find out what colors appear on the levels above which a person could not climb. See how far you can go.
To run AI, you need a universal NES / Famicom FCEUX emulator . Artificial Intelligence was developed for FCEUX 2.2.2 , the newest version of the emulator at the time of writing.
You will also need a Nintendo Tetris ROM file (US version). Try searching it on google .
Extract
Run FCEUX. From the menu, select File | Open ROM ... In the Open File dialog box, select the Nintendo Tetris ROM file and click Open. The game will start.
From the menu, select File | Lua | New Lua Script Window ... In the the Lua Script window, enter the path to
The script on Lua will redirect you to the first screen of the menu. Leave the A-Type game type, and you can choose any music. On slow computers, music can play very jerky, then you should turn it off. Press Start (Enter) to go to the next menu screen. In the second menu, you can use the arrow keys to change the starting level. Click on Start to start the game. And here management intercepts AI.
If, after selecting a level in the second screen of the menu, to hold down the button of the gamepad A (you can change the keyboard layout in the Config | Input ... menu) and click Start, the initial level will be 10 more than the selected value. The maximum elementary level is nineteenth.
To make the game go faster, open the Lua script in a text editor. At the beginning of the file, find the following line.
Replace
Save the file. Then click the Restart button in the Lua Script window.
Each figure Tetrimino corresponds to a single-letter name that resembles its shape.

Nintendo Tetris designers arbitrarily set up the tetrimino order shown above. The figures are shown in the orientation in which they appear on the screen, and the diagram creates an almost symmetrical picture (perhaps, therefore, this order was chosen). The sequence index gives each tetrimino a unique numeric ID. Sequence and type identifiers are important at the programming level; in addition, they manifest themselves in the order of the figures displayed in the statistics field (see below).

The 19 orientations used in Nintendo Tetris are tetrimino encoded in a table located at the
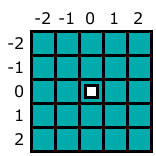
In the figure above, the white square indicates the center of the matrix, the reference point for the rotation of the shape.
Below is a graph of the orientation table.

The orientation identifier (table index) is shown in hexadecimal form in the upper right corner of each matrix. And the mnemonic invented for this project is shown in the upper left corner.
Matrices containing the orientation of the figures during creation are marked with a white frame.
Tetrimino I, S and Z could be given 4 separate orientations, but the creators of Nintendo Tetris decided to limit themselves to two. Furthermore,
The orientation table also contains tile values for each square in each oriented figure. However, after careful study it becomes clear that the values for one type of tetrimino are always the same.
The values of the tiles are the indices of the table (pseudo-color) pattern shown below.

Tiles
For the curious, I will say that ostriches and penguins are used in the endings of the B-Type mode. This topic is discussed in detail in the "Endings" section.
Below is the result of the ROM modification after replacing

Heart tiles remain on the playing field even after the modified Ts are locked in place. As stated below in the “Creating Tetrimino” section, this means that the playing field stores the actual values of the indexes of tiles played by Tetrimino.
The programmers of the game made it possible to use 4 separate tiles for each piece, and not just one constant type of squares. This is a useful feature that can be used to modify the look of the game. There is a lot of empty space for new tiles in the pattern table that can give each Tetrimino a unique appearance.
The coordinates of the squares are very easy to manipulate. For example, below is a modified version of the first four triples in the orientation table.
This change is similar to the following:
The result is a split tetrimino.
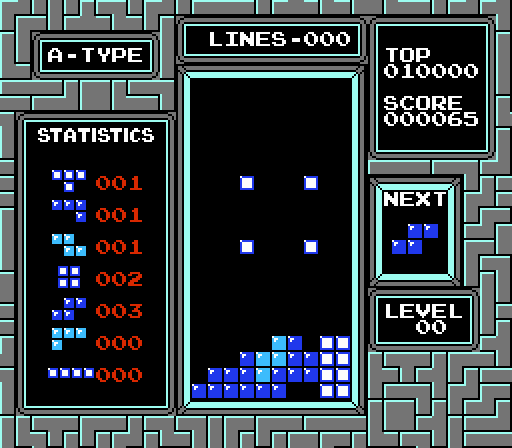
When moving a divided tetrimino, its squares cannot go beyond the boundaries of the playing field and cannot pass through the previously blocked figures. In addition, the game prohibits a rotation in this orientation, if it leads to a square falling outside the boundaries of the playing field or to the fact that the square is superimposed on the square that is already lying.
A divided tetrimino is locked in place when there is support for any of its squares. If the figure is blocked, the squares hanging in the air continue to hang.
The game deals with divided tetrimino as with any normal figure. This makes us understand that there is no additional table that stores the metadata of the figures. For example, there might be a table storing the dimensions of the bounding box of each orientation to check for collisions with the perimeter of the playing field. But such a table is not used. Instead, the game simply performs checks of all four squares right before the figure manipulations.
In addition, the coordinates of the squares can be any value; they are not limited by interval
In the graphical illustration of the orientation table, the rotation consists in the transition from the matrix to one of the matrices on the left or right, with the transfer of a number if necessary. This concept is encoded in the table at
The mnemonics in the headers at the top can be interpreted as a sequence index or key for distribution. For example, turning counterclockwise
The turn table encodes chained sequences of orientations IDs; therefore, we can modify the records so that the rotation transforms one type of tetrimino into another. This technique can potentially be used to benefit from an unused row in the orientation table.
Before the table of turns there is a code for access to it. To rotate counterclockwise, the index of the turn table is subtracted by doubling the orientation ID. By adding 1 to it, we get the rotation index clockwise.
Coordinates
The code uses a temporary variable to back up the orientation ID. Later, after changing the orientation, the code checks that all four squares are within the boundaries of the playing field and none of them overlaps the already lying squares (the verification code is located at the address
Counting from the cross, the NES controller has eight buttons, the status of which is represented by the address bit
For example, the
On the other hand,
The Nintendo Tetris game board consists of a matrix with 22 rows and 10 columns so that the top two rows are hidden from the player.

As shown in the code below, when creating a Tetrimino shape, it is always located in the coordinates of the

None of the creation matrices have squares above the starting point. That is, when creating a Tetrimino, all four of its squares are immediately visible to the player. However, if a player quickly rotates a piece before it has time to fall, part of the piece will be temporarily hidden in the first two lines of the playing field.
We usually think that the game ends when the heap reaches the top. But in fact it is not so. The game ends when it is no longer possible to create the next figure. That is, before the appearance of the figure, all four cells of the playing field should be free, corresponding to the positions of the squares created by Tetrimino. The figure may be blocked in place in such a way that some of its squares will appear in negatively numbered lines, and the game will not end; however, in Nintendo Tetris, negative lines are an abstraction that only applies to active Tetrimino. After the shape is blocked (becomes lying), only squares in lines from zero and more are written to the field. Conceptually, it turns out that negatively numbered lines are automatically cleared after blocking.
The visible area of the playing field 20 × 10 is stored at the address
When creating a shape, three lookup tables are used. If there is an arbitrary orientation ID, the table at the address
For example, all orientations J are attached to
The table at the address
We will look at the third lookup table in the next section.
The Nintendo Tetris as a pseudorandom number generator (PRNG) used a 16-bit linear feedback shift register (linear feedback shift register, LFSR) in Fibonacci configuration. 16-bit value is stored as big-endian by addresses
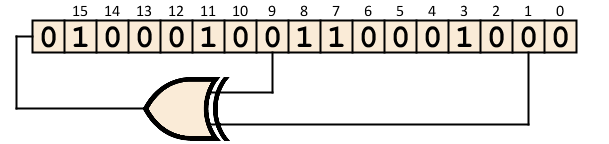
This process takes place at
And all this code can be pressed down to one line.
This PRNG continuously and deterministically generates 32,767 unique values, starting each cycle from the initial seed. This is one less than half of the possible numbers that can fit in a register, and any value in this set can be used as a seed. Many of the values outside the set create a chain that will eventually lead to a number from the set. However, some seed numbers result in an infinite sequence of zeros.
To estimate the performance of this PRNG roughly, I generated a graphical representation of the values it creates, based on a sentence with RANDOM.ORG .

When creating an image, PRNG was used as a pseudo-random number generator, rather than 16-bit integers. Each pixel is colored based on the value of bit 0. The image has a size of 128 × 256, that is, it covers the entire sequence.
Except for the barely noticeable stripes on the top and left sides, it looks random. No obvious patterns appear.
After launching, the PRNG constantly shuffles the register, triggering at least once a frame. This does not happen not only on the splash screen and menu screens, but also when tetrimino drops between the figure creation operations. That is, the figure appearing next depends on the number of frames taken by the player to place the figure. In fact, the game relies on the randomness of the actions of the person interacting with it.
During the creation of the figure, the code at the address
At the first stage of the conversion, the counter of the created figures is added to the upper byte. Then a mask is applied to save only the lower 3 bits. If the result is not 7, then this is the correct type of tetrimino, and if it is not the same as the previous selected figure, then the number is used as an index in the shape creation table. Otherwise, the next pseudo-random number is generated and a mask is applied to obtain the lower 3 bits of the upper byte, and then the previous shape creation orientation ID is added. Finally, a modular operation is performed to obtain the correct type of tetrimino, which is used as an index in the shape creation table.
Since the processor does not support division with remainder, this operator is emulated by repeatedly subtracting 7, until the result is less than 7. Division with remainder is applied to the sum of the upper byte with the mask and the previous ID of creating the shape. The maximum value of this sum is equal to 25. That is, in order to reduce it to the remainder of 4, only 3 iterations are required.
At the beginning of each game, the shape creation ID orientation (
When used in the sum of the previous ID, the orientation of the shape creation, and not the previous type, Tetrimino adds distortion, because the values of the orientation ID are not evenly distributed. This is shown in the table:
Each cell contains the type of tetrimino, calculated by adding the orientation ID of the created figure (column) to the 3-bit value (line), and then applying the remainder of the division by 7 to the sum. Each line contains duplicates because
There are 56 possible input combinations, and if the resulting types are evenly distributed tetrimino, then we can expect that in the table shown above each type should appear exactly 8 times. But as shown below, it is not.
T and S appear more often, and L and I - less. But skewed code using orientation ID is not executed every time a subroutine is called.
Suppose that a PRNG does create a sequence of uniformly distributed statistical independent values. In fact, this is a fair assumption, considering how the game tries to get the correct chance from the player’s actions. Adding the number of created figures to the address
In a set of 224 created tetrimino, the expectation is 32 instances for each type. But in fact, the code creates the following distribution:
That is, clearing 90 lines and reaching level 9, the player will receive one extra T and S and one less L and I than statistically expected.
Tetriminos are selected with the following probabilities:
It seems that in the statement that the “long stick” I never appears when it is needed, there is part of the truth (at least for Nintendo Tetris).
Nintendo Tetris uses Delayed Auto Shift (DAS). Pressing Left or Right instantly moves tetrimino one cell horizontally. While holding one of these directional buttons causes the game to automatically move the piece every 6 frames with an initial delay of 16 frames.
This type of horizontal movement is controlled by the code at
Automatic descent speed is a function of the level number. Speeds are encoded as the number of rendered frames per descent in the table located at
There are 30 entries in the table. After level 29, the value of frames per descent is always 1. The
integer number of frames per descent is not a particularly detailed way of describing speed. As shown in the graph below, the rate increases exponentially with each level. In fact, level 29 is twice as fast as level 28.
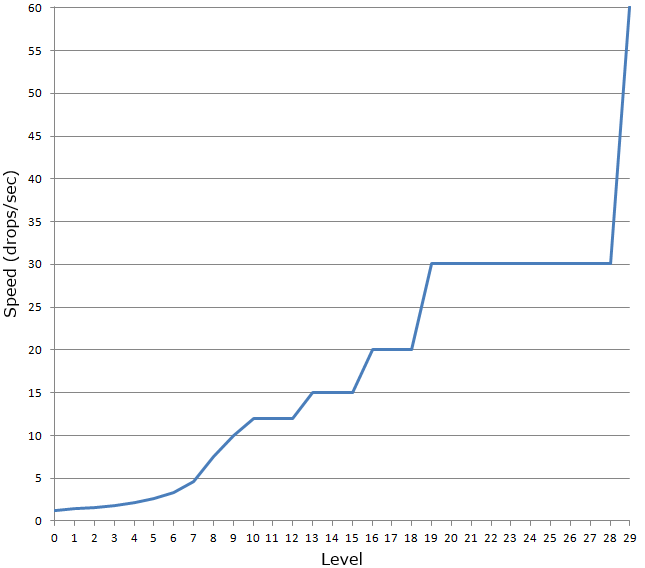
At 1 frame / descent, the player has no more than 1/3 of a second to position the piece before it starts moving. At this speed of descent, DAS does not allow the figure to reach the edges of the playing field before blocking in place, which means for most people a quick end to the game. However, some players, in particular, Toru Akerlund , managed to defeat DAS with a quick vibration of the cross buttons (
If the automatic and player controlled descent (by pressing "Down") coincide and occur in one frame, the effect does not add up. Either or both of these events cause the shape to drop down exactly one cell in this frame.
The descent control logic is located at
The increment
In addition, it
Potentially soft descent can increase the number of points.
A check that prevents a player from performing a soft descent during a horizontal shift of a figure complicates the set of points. It means that the last move before blocking a piece in place must be “Down”.
When a descent occurs,
Hard descent (instant figure drop) is not supported in Nintendo Tetris.
The Nintendo Tetris handbook has an illustrated example of how to do a slip:

Sliding consists of shifting along the surface of other pieces or along the floor of the playing field. It is usually used to stick a piece under a hanging square. The slide can be performed until the drop timer reaches the speed of descent, after which the figure will be locked in place. Below is an animated example.

On the other hand, scrolling allows you to stick figures into spaces that cannot be reached in any other way (see below).

Like sliding, scrolling is impossible without blocking delay. But beyond that, scrolling exploits the way in which the game manipulates figures. Before moving or rotating the figure, the game checks that after changing the position, all the squares of tetrimino will be in empty cells within the boundaries of the playing field. Such a check, as shown below, does not prevent rotation through the nearest filled blocks. As stated in the “Tetrimino Description” section, each row of the orientation table contains 12 bytes; therefore, the index in this table is calculated by multiplying the active orientation Tetrimino ID by 12. As shown below, all multiplications in the subroutine are performed using shifts and addition.
Each iteration of the cycle shifts the position of the tetrimino by the relative coordinates of one of the squares from the orientation table in order to obtain the corresponding position of the cell on the playing field. She then checks that the coordinates of the cell are within the boundaries of the playing field, and that the cell itself is empty.
The comments describe more clearly the way in which line spacing checks are performed. In addition to the cells in the visible lines, the code considers two hidden lines above the playing field as the legal positions of the squares without using the compound condition. This works because in the additional code the negative numbers represented by single-byte variables are equivalent to values greater than 127. In this case, the minimum value is −2, which is stored as
The playing field index is the amount
It is strange that the interval check

As shown below, you can even perform a slide with scrolling.

The AI uses all the movement capabilities available in Nintendo Tetris, including sliding and scrolling.
After reaching level 30 it seems that the level is reset to zero.
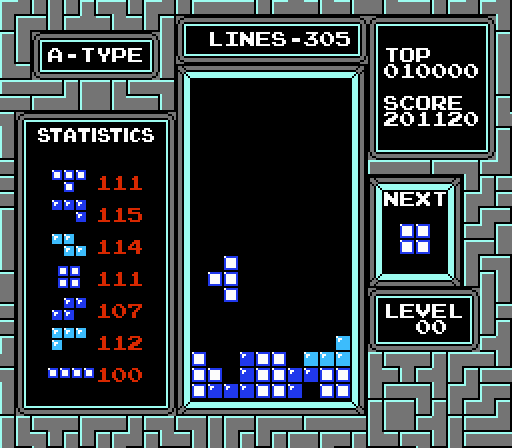
But level 31 shows that something else is happening:

The displayed level values are located in the table at
As shown below, the pattern table is ordered in such a way that tiles with

Unfortunately, it seems that the game designers assumed that no one would pass level 29, and therefore decided to insert only 30 records into the table. Strange display values are different bytes after the table. To indicate the level number, only one byte is used (at the address
The first 20 ordinal values are actually another table in which the offsets on the playing field for each of the 20 rows are stored. Since the playing field starts with and each row contains 10 cells, the address of an arbitrary cell is: Given that the processor does not directly multiply, this lookup table provides an extremely fast way to get the piece. The corresponding table is the next 40 bytes. It contains 20 addresses in little endian format for a nametable 0 (a VRAM memory area containing background tile values). They are pointers to the playing field offset lines on . The remaining bytes, of which the displayed level values are composed, are instructions.
The number of filled rows and tetrimino statistics occupy 2 bytes each at the following addresses.
Essentially, these values are stored as 16-bit packed BCD little endian. For example, below is the number of rows equal to 123. The bytes are counted from right to left for the decimal digits to go in order.

However, the game designers assumed that none of the values would be greater than 999. Therefore, the display logic correctly processes the first byte as a packed BCD, where each nibble is used as a tile value. But the entire second byte is actually used as the top decimal digit. When the bottom digits go from

After the row is cleared, the following code is executed to increment the number of rows. Checks are performed for the middle and lower digits so that they remain in the range from 0 to 9. But the upper digit can be increased indefinitely. If after the increment of the number of rows, the lower digit is 0, then this means that the player has just completed a set of 10 rows and you need to increase the level number. As can be seen from the code below, an additional check is performed before the increment of the level. The second check is related to the selected initial level. To go to any level , regardless of the initial level, the player must clear
To perform this check, the value of the filled rows is copied from

However, at the address
The table shows the expected number of rows required for the transition at each initial level. It is compared with the fact that because of the bug is actually happening.
The expected number coincides with the true for the initial levels of 0–9. In fact, the coincidence for entry level 9 is random; 10–15 also moves to the next level with 100 rows, because it
I suspect that the bug is related to design changes in the later stages of development. Look at the menu screen, which allows the player to choose the starting level.

There is no explanation of how to start with levels above 9. But in the Nintendo Tetris guide booklet this secret is revealed:

It seems that this hidden feature was invented at the last moment. Perhaps it was added very close to the release date, which made it impossible to fully test it.
In fact, the verification of the initial series contains a second error associated with the output of values for the interval. Below are the comments in the code that best explain what is happening at a low level. The comparison is performed by subtracting and checking the sign of the result. But the signed one-byte number is limited to the interval from −128 to 127. If the difference is less than −128, the number is transferred and the result becomes a positive number. This principle is explained in the comments to the code. When checking that the difference is in this interval, you need to take into account that the level number with increment to values greater than 255 performs a transfer to 0, and
These effects overlap, creating periods in which the level number erroneously remains unchanged. Periods occur at regular intervals of 2,900 rows, starting at 2,190 rows, and last for 800 rows. For example, from 2190 (

The next period happens from 5090 to 5890, the level is constantly equal to
At each level, tetrimino tiles are assigned 4 unique colors. Colors are taken from the table located at

Values correspond to the NES color palette.

The first 2 colors of each record are always black and white. However, in fact, the first color is ignored; regardless of the value, it is considered to be a transparent color through which a solid black background peeps through.
Access to the color table is performed in the subroutine at
However, as mentioned in the previous section, subtraction and branching based on the sign of the difference is used in comparison. A signed single-byte number is limited to an interval from −128 to 127. The updated comments below reflect this principle. The comments below are even more simplified. Such a formulation reveals an error in the code. The division operation with the remainder is completely skipped for levels from 138 and above. Instead, the index is assigned directly to the level number, which provides access to the bytes far beyond the end of the color table. As shown below, it can even lead to almost invisible tetrimino.
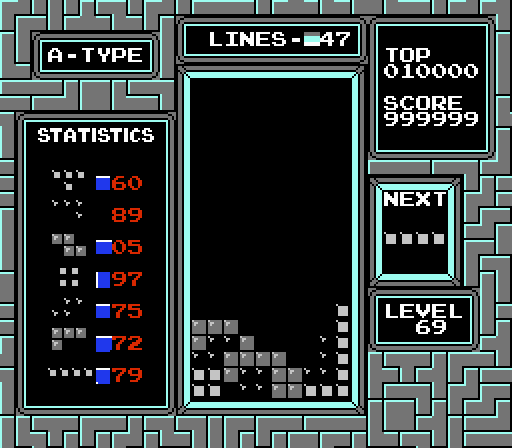
Below are the colors of all 256 levels. The tiles are arranged in 10 columns to emphasize the cyclic use of the color table, broken at level 138. Rows and columns in the headers are indicated in decimal form.

After 255, the level number returns to 0.
In addition, as mentioned in the previous section, some levels do not change until 800 rows are removed. During these long levels of color remain unchanged.
The game mode stored at the address
As shown above, the game has a cleverly written subroutine that performs the role of a switch statement using the little endian transition table, located immediately after the call. The list above shows the addresses of all game modes. Note that the “Game” and “Demo” modes use the same code. This routine never returns. Instead, the code uses the return address; usually it indicates the instruction immediately following the jump to the subroutine (minus 1 byte), but in this case it points to the jump table. The return address is removed from the stack and saved to - . After saving the jump table address, the code uses the value in register A as an index and performs the corresponding jump.
The code can use this switch-subroutine, as long as the indices are close to 0 and there are no gaps between possible cases or few of them.
The game starts with a screen that shows legal notice.

At the bottom of the screen, Alexey Pajitnov is mentioned as an inventor, designer and programmer of the first Tetris. In 1984, while working as a computer developer at the Dorodnitsyn Computing Center (a leading research institute of the Russian Academy of Sciences in Moscow), he developed a prototype game for Electronics-60 (the Soviet clone DEC LSI-11 ). The prototype was developed for a green monochrome text mode, in which the squares are denoted by pairs of square brackets
Unfortunately, due to the peculiarities of the Soviet Union of that time, their attempts to monetize the game were not crowned with success, and in the end they decided to share the PC version with their friends for free. From that moment on, Tetris began to spread around the country and beyond its borders, copied from a floppy disk to a floppy disk. But since the game was developed by employees of a state institution, the state was its owner, and in 1987 the organization responsible for the international trade in electronic technology took up licensing the game (ELorg)). The abbreviation V / O on the legal information screen can be abbreviated from Version Originale. Andromeda, a
British software development company, tried to get rights to Tetris and, before the deal was completed, slanted the game to other suppliers, for example, the British computer game publisher Mirrorsoft . Mirrorsoft, in turn, sublicensed it to Tengen , a subsidiary of Atari Games. Tengen granted Bullet-Proof Software the rights to develop games for computers and consoles in Japan, which resulted in Tetris for Nintendo Famicom . Below is his legal information screen.
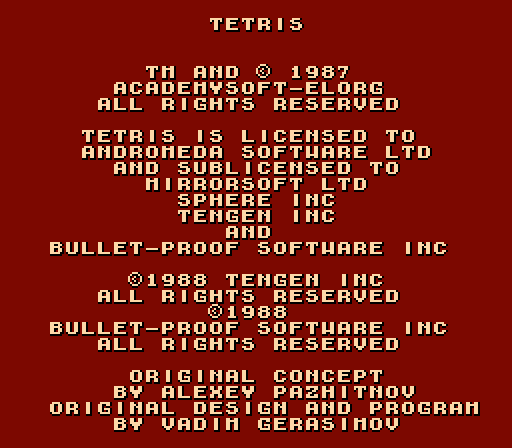
Interestingly, in this version the schoolboy Vadim Gerasimov is called the original designer and programmer.
Trying to get the rights to the portable version for the upcoming Game Boy console, Nintendo used Bullet-Proof Software to make a successful deal directly with ELORG. In the process of concluding a deal, ELORG revised its contract with Andromeda, adding that Andromeda received rights only for games for computers and arcade machines. Because of this, Bullet-Proof Software had to pay ELORG license fees for all the cartridges sold to Famicom, because the rights it received from Tengen turned out to be fake. But thanks to reconciliation with Bullet-Proof Software's ELORG, we finally managed to get worldwide rights to console games for Nintendo.
Bullet-Proof Software sublicensed the rights to Nintendo portable games and together they developed Game Boy Tetris, which is reflected in the legal information screen shown below.
Having obtained worldwide rights to console games, Nintendo developed the Tetris version for NES, which we study in this article. Then Bullet-Proof Software sublicensed Nintendo's rights, which allowed it to continue selling cartridges for Famicom in Japan.
This was followed by a complex legal dispute. Both Nintendo and Tengen demanded that the opposing side stop producing and selling their version of the game. As a result, Nintendo won, and hundreds of thousands of Tengen Tetris cartridges were destroyed. The court’s verdict also prohibited several other companies like Mirrorsoft from creating console versions.
Pajitnov never received any deductions from ELORG or the Soviet state. However, in 1991 he moved to the USA and in 1996 with the support of the owner of Bullet-Proof SoftwareHenk Rogers co-founded The Tetris Company , which enabled him to profit from versions for mobile devices and modern consoles.
It is curious to look at the legal information screen as a window, giving an idea of the modest birth of the game and the ensuing battles for intellectual property rights, because for most players this screen is just an annoying obstacle, the disappearance of which seems to wait forever. The delay is set by two counters, sequentially performing a counting from 255 to 0. The first phase cannot be skipped, and the second is skipped by pressing the Start button. Therefore, the legal information screen is displayed for at least 4.25 seconds and not more than 8.5 seconds. However, I think that most of the players give up, stopping pressing Start during the first interval, and because of this it is waiting for complete completion.
The timing of the phases, as well as the rest of the game, is controlled by a nonmaskable interrupt handler called at the beginning of each vertical blanking interval — a short period of time between rendering television frames. That is, every 16.6393 milliseconds, normal program execution is interrupted by the following code. The handler starts by transferring the values of the main registers to the stack and retrieves them after completion in order not to interfere with the interrupted task. The call updates VRAM, transforming the description of the memory model into what is displayed on the screen. Next, the handler reduces the value of the legal information screen counter, if it is greater than zero. Call
The flag is
This blocking subroutine is used in two stages of legal information screen timings that are executed one after the other. The AI script on Lua bypasses this delay by assigning the value 0 to both counters.
The demo shows approximately 80 seconds of pre-recorded gameplay. It does not just display the video file, but uses the same engine as in the game. During playback, two tables are used. The first one, located at the address
When creating a figure, it is either chosen randomly or read from a table, depending on the mode. Switching occurs at
Because of this effect, this scheme can give us an unlimited, but reproducible sequence of pseudo-random ID orientations of the created figures. The code will work because any arbitrary address in a varying sequence of bytes does not allow us to determine where the table ends. In fact, the sequence at an address
During the initialization of the demo mode, the index of the table (
The second demo table contains a record of gamepad buttons, encoded in pairs of bytes. The bits of the first byte correspond to the buttons.
The second byte stores the number of frames during which the combination of buttons is pressed.
The table takes the address
This suggests that developers could run the program partially or completely in RAM.
To get around this obstacle, I created
To record your own demo, run FCEUX and download the Nintendo Tetris ROM file (File | Open ROM ...). Then open the Lua Script window (File | Lua | New Lua Script Window ...), go to the file or enter the path. Click the Run button to start the demo recording mode, and then click the FCEUX window to switch focus to it. You can control the shapes until the table of buttons is filled. After that, the game will automatically return to the splash screen. Click Stop in the Lua Script window to stop the script. Recorded data will appear in the Output Console, as shown in the figure below.

Select all content and copy to clipboard (Ctrl + C). Then run the Hex Editor (Debug | Hex Editor ...). From the Hex Editor menu, select View | ROM File, and then File | Goto Address. In the Goto dialog box, enter 5D10 (the address of the table of demo buttons in the ROM file) and click Ok. Then paste the contents of the clipboard (Ctrl + V).

Finally in the FCEUX menu, select NES | Reset If you managed to repeat all these steps, then the demo should be replaced with your own version.
If you want to save the changes, in the Hex Editor menu, select File | Save Rom As ... and enter the name of the modified ROM file, and then click Save.
Similarly, you can customize the sequence created by Tetrimino.
As mentioned above, the majority of players cannot cope with the speed of descent of figures at level 29, which quickly leads to the completion of the game. Therefore, the players he became associated with the name "screen of death." But from a technical point of view, the death screen does not allow the player to go further because of the bug, in which the quick descent actually turns out to be not a bug, but features. The designers were so kind that they allowed the game to continue as long as the player was able to withstand superhuman speed.
This screen of death occurs on about 1,550 rows removed. It manifests itself in different ways. Sometimes the game reloads. In other cases, the screen just turns black. Usually, the game freezes (“freezes”) immediately after deleting a row, as shown below. Such effects are often preceded by random graphic artifacts.

The screen of death is the result of a bug in the code that adds points when deleting rows. The six-character account is stored as a 24-bit packed BCD little endian and is located at
As shown below, the multiplication is simulated by a cycle that adds points to the score. It is executed after blocking the shape, even if no rows are cleared. Unfortunately, the Ricoh 2A03 does not have the 6502 processor binary-decimal mode; he could greatly simplify the body of the cycle. Instead, the addition is done in steps, using the binary mode. Any digit that exceeds the value of 9 after the addition is essentially obtained by subtracting 10 and the increment of the digit on the left. For example, that is converted to . But this scheme is not fully protected. Take : verification is not able to convert the result to
It takes time to complete this long and complex cycle. At large levels, a large number of iterations affect the timing of the game, because the generation of each frame takes more than 1/60 of a second. All this as a result leads to different manifestations of the “death screen”.
The AI script on Lua limits the number of iterations in the loop to 30 — the maximum value that the designers intended could be reached by the players, which makes it possible to eliminate the screen of death.
In the Nintendo Tetris guide booklet, an A-Type game is described as:

The game rewards players who score large enough points in one of the five animations of the endings. The choice of ending is entirely based on the two leftmost digits of the six-digit count. As shown below, to get one of the endings, the player must score at least 30,000 points. It is worth noting that - - this is a mirror of addresses - . The account is duplicated by addresses - . After passing the first test, the animation of the ending is selected with the following switch statement.
At the end of the rocket of increasing size are launched from the launch pad next to St. Basil's Cathedral. In the fourth ending, the Buran spacecraft is shown - the Soviet version of the American Space Shuttle. In the best ending, the cathedral itself rises in the air, and a UFO hangs above the launch pad. Below is a picture of each ending and the score associated with it.
In the B-Type game mode, another test is implemented, which is described in the Nintendo Tetris guide booklet as follows:

If the player successfully clears 25 rows, the game shows the ending, depending on the initial level. The endings for levels 0–8 consist of animals and objects flying or running in the frame, mysteriously passing behind St. Basil's Cathedral. A UFO from the best ending of the A-Type mode appears in the ending 3. In the ending 4, extinct flying pterosaurs appear, and in the ending 7 mythical flying dragons are shown. In the endings 2 and 6, wingless birds are shown: running penguins and ostriches. In the end 5, the sky is filled with GOOD airships (not to be confused with Goodyear airships). And in the end 8, a lot of “Burans” rush through the screen, although in reality it was only one.
The initial height (plus 1) is used as a multiplier, rewarding the player with a large number of animals / objects for increased complexity.
In the best B-Type ending, the castle is filled with characters from the Nintendo universe: Princess Peach claps her hands, Kid Icarus plays the violin, Donki Kong knocks on the big drum, Mario and Luigi dance, Bowser plays the accordion, Samus plays the cello, Link - on the flute, while the domes of St. Basil’s Cathedral soar into the air. From the initial height depends on the number of these elements shown in the end. Below are the images of all 10 endings.
The AI can quickly clear all 25 rows required in the B-Type mode at any initial level and height, allowing you to view any of the endings. It is also worth assessing how cool he is with large piles of random blocks.
In the endings 0–8, up to 6 objects can move in the frame. The y coordinates of the objects are stored in a table located at
The central table of the pattern we considered above, it is used to display tetrimino and the playing field. Interestingly, it contains the entire alphabet, while others contain only part of it to save space. But even more interesting are the sprites of the aircraft and the helicopter in the pattern table on the left; they do not appear in the endings or in other parts of the game. It turned out that the plane and the helicopter have indexes sprites


Unfortunately, the helicopter supports are not displayed, but the main and tail rotors are beautifully animated.
Nintendo Tetris contains an unfinished two-player mode, which can be turned on by changing the number of players (

There is no border between the fields, because the central background area has a solid black color. The values
But if you do not take into account these problems, the mode is quite playable. Each player can independently control the pieces in the corresponding playing field. And when a player enters Double, Triple or Tetris (that is, clears two, three or four rows), trash cans appear at the bottom of the playing field with one missing square.
An additional field is located at
Probably, this interesting mode was abandoned due to the tight development schedule. And perhaps he was left unfinished on purpose. One of the reasons Tetris was selected as the game that came with the Nintendo Game Boy was that it encouraged him to buy Game Link Cable- an accessory that connected together two Game Boy to launch 2 player versus mode. This cable added an element of "sociality" to the system - pushing friends to buy a Game Boy to join in the fun. Perhaps Nintendo feared that if in the console version of the game there would be 2 player versus mode, then the Tetris advertising power, which stimulated the purchase of a Game Boy, could be weakened.
Background music is turned on when
You can listen to unused screen saver music here . In the game itself during the screen saver nothing sounds.
Music-1 is a version of Dance of the Fairy Drazhe , music for the ballerina from Tchaikovsky 's Nutcracker, the third act of the pas de Vallors . The ending music is a variation of The Bullfighter's Couplets , arias from the opera by Carmen Georges Bizet. These compositions are arranged by the composer for the rest of the music of the game Hirokazu Tanaka . Music-2 was inspired by traditional Russian folk songs. Music-3 is mysterious, futuristic and tender; for a while, it was the melody of a Nintendo of America customer support phone call.
To help the player get into a state of panic, when the height of the heap approaches the ceiling of the playing field, a fast paced version of the background music (
Interestingly, among the musical compositions there is no " Korobeinikov ", a famous theme, sounding in Game Boy Tetris.
Sound effects are triggered by recording to
During gameplay, the current state of the game is represented by an integer number at
Code branching, depending on the game state, occurs at the address

The curtain is drawn down from the top of the playing field, going down one line every 4 frames.
The lines of the playing field are incrementally copied to VRAM for display. The index of the current copied string is contained in
Manipulations with VRAM occur during the vertical blanking interval, which is recognized by the interrupt handler described in the “Legal Information Screen” section. It calls the subroutine shown below (marked in the comments of the interrupt handler as
Part of the rendering mode is
The state handler
Unlike the game state
This is done only because it is
The block starting with
The easiest way to do this and get the most, waiting for the demo to collect Tetris (there will be 2 in the demo). As soon as you see the screen flicker, press Start.

After starting a new game, the screen will continue to flicker. All this thanks to the following code, called the interrupt handler. In fact, if you let the first piece automatically descend to the floor of the playing field, the score will increase by an even greater value, because ( ) also saves its value from the demo. This is true even in cases where the demo did not fill a single row. is not reset until the Down button is pressed. Moreover, if you press Start during the animation of cleaning the rows of the Tetris combination in demo mode, and then wait for the demo to start again, the demo will not only score points for Tetris, but will also confuse the entire timing. As a result, the demo will lose the game. After the end of the game curtain, you can return to the splash screen by clicking on Start.
The game state
The game state
The game state is
The game state is
And now, finally, the main game loop:

Try it yourself
about the project
For those who lack the perseverance, patience and time needed to master Nintendo Tetris, I created an AI capable of playing on my own. You can finally get to level 30 and beyond. You will see how to get the maximum points and watch the endless changes in the counters of rows, levels and statistics. Find out what colors appear on the levels above which a person could not climb. See how far you can go.
Requirements
To run AI, you need a universal NES / Famicom FCEUX emulator . Artificial Intelligence was developed for FCEUX 2.2.2 , the newest version of the emulator at the time of writing.
You will also need a Nintendo Tetris ROM file (US version). Try searching it on google .
Download
Extract
lua/NintendoTetrisAI.luafrom this zip file with source code .Launch
Run FCEUX. From the menu, select File | Open ROM ... In the Open File dialog box, select the Nintendo Tetris ROM file and click Open. The game will start.
From the menu, select File | Lua | New Lua Script Window ... In the the Lua Script window, enter the path to
NintendoTetrisAI.luaor click the Browse button to find it. After that click Run. The script on Lua will redirect you to the first screen of the menu. Leave the A-Type game type, and you can choose any music. On slow computers, music can play very jerky, then you should turn it off. Press Start (Enter) to go to the next menu screen. In the second menu, you can use the arrow keys to change the starting level. Click on Start to start the game. And here management intercepts AI.
If, after selecting a level in the second screen of the menu, to hold down the button of the gamepad A (you can change the keyboard layout in the Config | Input ... menu) and click Start, the initial level will be 10 more than the selected value. The maximum elementary level is nineteenth.
Configuration
To make the game go faster, open the Lua script in a text editor. At the beginning of the file, find the following line.
PLAY_FAST = falseReplace
falsewith trueas shown below. PLAY_FAST = trueSave the file. Then click the Restart button in the Lua Script window.
Nintendo Tetris Mechanics
Tetrimino Description
Each figure Tetrimino corresponds to a single-letter name that resembles its shape.

Nintendo Tetris designers arbitrarily set up the tetrimino order shown above. The figures are shown in the orientation in which they appear on the screen, and the diagram creates an almost symmetrical picture (perhaps, therefore, this order was chosen). The sequence index gives each tetrimino a unique numeric ID. Sequence and type identifiers are important at the programming level; in addition, they manifest themselves in the order of the figures displayed in the statistics field (see below).

The 19 orientations used in Nintendo Tetris are tetrimino encoded in a table located at the
$8A9Cmemory address of the NES console. Each figure is represented as a sequence of 12 bytes, which can be divided into triples (Y, tile, X)that describe each square in the figure. The above hex coordinate values above $7Fdenote negative integers ( $FF= −1, a $FE = −2).
At the bottom of the table there is one unused record, potentially giving the possibility of adding another orientation. However, in different parts of the code it means that the orientation identifier of the active Tetrimino is not assigned a value.
For ease of reading below are the coordinates of the squares in decimal form.
All orientations are placed in a 5 × 5 matrix. ; Y0 T0 X0 Y1 T1 X1 Y2 T2 X2 Y3 T3 X3
8A9C: 00 7B FF 00 7B 00 00 7B 01 FF 7B 00 ; 00: T up
8AA8: FF 7B 00 00 7B 00 00 7B 01 01 7B 00 ; 01: T right
8AB4: 00 7B FF 00 7B 00 00 7B 01 01 7B 00 ; 02: T down (spawn)
8AC0: FF 7B 00 00 7B FF 00 7B 00 01 7B 00 ; 03: T left
8ACC: FF 7D 00 00 7D 00 01 7D FF 01 7D 00 ; 04: J left
8AD8: FF 7D FF 00 7D FF 00 7D 00 00 7D 01 ; 05: J up
8AE4: FF 7D 00 FF 7D 01 00 7D 00 01 7D 00 ; 06: J right
8AF0: 00 7D FF 00 7D 00 00 7D 01 01 7D 01 ; 07: J down (spawn)
8AFC: 00 7C FF 00 7C 00 01 7C 00 01 7C 01 ; 08: Z horizontal (spawn)
8B08: FF 7C 01 00 7C 00 00 7C 01 01 7C 00 ; 09: Z vertical
8B14: 00 7B FF 00 7B 00 01 7B FF 01 7B 00 ; 0A: O (spawn)
8B20: 00 7D 00 00 7D 01 01 7D FF 01 7D 00 ; 0B: S horizontal (spawn)
8B2C: FF 7D 00 00 7D 00 00 7D 01 01 7D 01 ; 0C: S vertical
8B38: FF 7C 00 00 7C 00 01 7C 00 01 7C 01 ; 0D: L right
8B44: 00 7C FF 00 7C 00 00 7C 01 01 7C FF ; 0E: L down (spawn)
8B50: FF 7C FF FF 7C 00 00 7C 00 01 7C 00 ; 0F: L left
8B5C: FF 7C 01 00 7C FF 00 7C 00 00 7C 01 ; 10: L up
8B68: FE 7B 00 FF 7B 00 00 7B 00 01 7B 00 ; 11: I vertical
8B74: 00 7B FE 00 7B FF 00 7B 00 00 7B 01 ; 12: I horizontal (spawn)
8B80: 00 FF 00 00 FF 00 00 FF 00 00 FF 00 ; 13: Unused$13-- { { X0, Y0 }, { X1, Y1 }, { X2, Y2 }, { X3, Y3 }, },
{ { -1, 0 }, { 0, 0 }, { 1, 0 }, { 0, -1 }, }, -- 00: T up
{ { 0, -1 }, { 0, 0 }, { 1, 0 }, { 0, 1 }, }, -- 01: T right
{ { -1, 0 }, { 0, 0 }, { 1, 0 }, { 0, 1 }, }, -- 02: T down (spawn)
{ { 0, -1 }, { -1, 0 }, { 0, 0 }, { 0, 1 }, }, -- 03: T left
{ { 0, -1 }, { 0, 0 }, { -1, 1 }, { 0, 1 }, }, -- 04: J left
{ { -1, -1 }, { -1, 0 }, { 0, 0 }, { 1, 0 }, }, -- 05: J up
{ { 0, -1 }, { 1, -1 }, { 0, 0 }, { 0, 1 }, }, -- 06: J right
{ { -1, 0 }, { 0, 0 }, { 1, 0 }, { 1, 1 }, }, -- 07: J down (spawn)
{ { -1, 0 }, { 0, 0 }, { 0, 1 }, { 1, 1 }, }, -- 08: Z horizontal (spawn)
{ { 1, -1 }, { 0, 0 }, { 1, 0 }, { 0, 1 }, }, -- 09: Z vertical
{ { -1, 0 }, { 0, 0 }, { -1, 1 }, { 0, 1 }, }, -- 0A: O (spawn)
{ { 0, 0 }, { 1, 0 }, { -1, 1 }, { 0, 1 }, }, -- 0B: S horizontal (spawn)
{ { 0, -1 }, { 0, 0 }, { 1, 0 }, { 1, 1 }, }, -- 0C: S vertical
{ { 0, -1 }, { 0, 0 }, { 0, 1 }, { 1, 1 }, }, -- 0D: L right
{ { -1, 0 }, { 0, 0 }, { 1, 0 }, { -1, 1 }, }, -- 0E: L down (spawn)
{ { -1, -1 }, { 0, -1 }, { 0, 0 }, { 0, 1 }, }, -- 0F: L left
{ { 1, -1 }, { -1, 0 }, { 0, 0 }, { 1, 0 }, }, -- 10: L up
{ { 0, -2 }, { 0, -1 }, { 0, 0 }, { 0, 1 }, }, -- 11: I vertical
{ { -2, 0 }, { -1, 0 }, { 0, 0 }, { 1, 0 }, }, -- 12: I horizontal (spawn)
In the figure above, the white square indicates the center of the matrix, the reference point for the rotation of the shape.
Below is a graph of the orientation table.

The orientation identifier (table index) is shown in hexadecimal form in the upper right corner of each matrix. And the mnemonic invented for this project is shown in the upper left corner.
u, r, d, l, hAnd v- a reduction of the «up, right, down, left , horizontal and vertical». For example, it is easier to indicate the orientation Jd, but not $07. Matrices containing the orientation of the figures during creation are marked with a white frame.
Tetrimino I, S and Z could be given 4 separate orientations, but the creators of Nintendo Tetris decided to limit themselves to two. Furthermore,
Zvand Svare not perfect mirror images of each other. Both are created by turning counterclockwise, which leads to an imbalance.The orientation table also contains tile values for each square in each oriented figure. However, after careful study it becomes clear that the values for one type of tetrimino are always the same.
| T | J | Z | O | S | L | I |
|---|---|---|---|---|---|---|
7B | 7D | 7C | 7B | 7D | 7C | 7B |
The values of the tiles are the indices of the table (pseudo-color) pattern shown below.

Tiles
$7B, $7Cand $7Dare located directly under "ATIS" from the word "STATISTICS". These are the three types of squares that tetrimino is made of. For the curious, I will say that ostriches and penguins are used in the endings of the B-Type mode. This topic is discussed in detail in the "Endings" section.
Below is the result of the ROM modification after replacing
$7Bwith $29. The heart is the tile under the P symbol in the pattern table for all T orientations.
Heart tiles remain on the playing field even after the modified Ts are locked in place. As stated below in the “Creating Tetrimino” section, this means that the playing field stores the actual values of the indexes of tiles played by Tetrimino.
The programmers of the game made it possible to use 4 separate tiles for each piece, and not just one constant type of squares. This is a useful feature that can be used to modify the look of the game. There is a lot of empty space for new tiles in the pattern table that can give each Tetrimino a unique appearance.
The coordinates of the squares are very easy to manipulate. For example, below is a modified version of the first four triples in the orientation table.
8A9C: FE 7B FE FE 7B 02 02 7B FE 02 7B 02 ; 00: T upThis change is similar to the following:
{ { -2, -2 }, { 2, -2 }, { -2, 2 }, { 2, 2 }, }, -- 00: T upThe result is a split tetrimino.

When moving a divided tetrimino, its squares cannot go beyond the boundaries of the playing field and cannot pass through the previously blocked figures. In addition, the game prohibits a rotation in this orientation, if it leads to a square falling outside the boundaries of the playing field or to the fact that the square is superimposed on the square that is already lying.
A divided tetrimino is locked in place when there is support for any of its squares. If the figure is blocked, the squares hanging in the air continue to hang.
The game deals with divided tetrimino as with any normal figure. This makes us understand that there is no additional table that stores the metadata of the figures. For example, there might be a table storing the dimensions of the bounding box of each orientation to check for collisions with the perimeter of the playing field. But such a table is not used. Instead, the game simply performs checks of all four squares right before the figure manipulations.
In addition, the coordinates of the squares can be any value; they are not limited by interval
[−2, 2]. Of course, much higher than this interval values will give us inapplicable figures that do not fit on the playing field. More importantly, as stated in the section “Game States and Rendering Modes”, when the shape is locked in place, the cleared line cleaning mechanism only scans the row offset from −2 to 1 from the shape's central square; a square with a coordinate youtside this interval will be unrecognized.Tetrimino rotation
In the graphical illustration of the orientation table, the rotation consists in the transition from the matrix to one of the matrices on the left or right, with the transfer of a number if necessary. This concept is encoded in the table at
$88EE.
To make it clearer, we will move each column from this table to the row of the table shown below. ; CCW CW
88EE: 03 01 ; Tl Tr
88F0: 00 02 ; Tu Td
88F2: 01 03 ; Tr Tl
88F4: 02 00 ; Td Tu
88F6: 07 05 ; Jd Ju
88F8: 04 06 ; Jl Jr
88FA: 05 07 ; Ju Jd
88FC: 06 04 ; Jr Jl
88FE: 09 09 ; Zv Zv
8900: 08 08 ; Zh Zh
8902: 0A 0A ; O O
8904: 0C 0C ; Sv Sv
8906: 0B 0B ; Sh Sh
8908: 10 0E ; Lu Ld
890A: 0D 0F ; Lr Ll
890C: 0E 10 ; Ld Lu
890E: 0F 0D ; Ll Lr
8910: 12 12 ; Ih Ih
8912: 11 11 ; Iv IvTu | Tr | Td | Tl | Jl | Ju | Jr | Jd | Zh | Zv | O | Sh | Sv | Lr | Ld | Ll | Lu | Iv | Ih | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Counterclock-wise | Tl | Tu | Tr | Td | Jd | Jl | Ju | Jr | Zv | Zh | O | Sv | Sh | Lu | Lr | Ld | Ll | Ih | Iv |
| Clockwise | Tr | Td | Tl | Tu | Ju | Jr | Jd | Jl | Zv | Zh | O | Sv | Sh | Ld | Ll | Lu | Lr | Ih | Iv |
The mnemonics in the headers at the top can be interpreted as a sequence index or key for distribution. For example, turning counterclockwise
Tugives us Tl, and turning clockwise Tugives Tr. The turn table encodes chained sequences of orientations IDs; therefore, we can modify the records so that the rotation transforms one type of tetrimino into another. This technique can potentially be used to benefit from an unused row in the orientation table.
Before the table of turns there is a code for access to it. To rotate counterclockwise, the index of the turn table is subtracted by doubling the orientation ID. By adding 1 to it, we get the rotation index clockwise.
88AB: LDA $0042
88AD: STA $00AE ; originalOrientationID = orientationID;
88AF: CLC
88B0: LDA $0042
88B2: ASL
88B3: TAX ; index = 2 * orientationID;
88B4: LDA $00B5
88B6: AND #$80 ; if (not just pressed button A) {
88B8: CMP #$80 ; goto aNotPressed;
88BA: BNE $88CF ; }
88BC: INX
88BD: LDA $88EE,X
88C0: STA $0042 ; orientationID = rotationTable[index + 1];
88C2: JSR $948B ; if (new orientation not valid) {
88C5: BNE $88E9 ; goto restoreOrientationID;
; }
88C7: LDA #$05
88C9: STA $06F1 ; play rotation sound effect;
88CC: JMP $88ED ; return;
aNotPressed:
88CF: LDA $00B5
88D1: AND #$40 ; if (not just pressed button B) {
88D3: CMP #$40 ; return;
88D5: BNE $88ED ; }
88D7: LDA $88EE,X
88DA: STA $0042 ; orientationID = rotationTable[index];
88DC: JSR $948B ; if (new orientation not valid) {
88DF: BNE $88E9 ; goto restoreOrientationID;
; }
88E1: LDA #$05
88E3: STA $06F1 ; play rotation sound effect;
88E6: JMP $88ED ; return;
restoreOrientationID:
88E9: LDA $00AE
88EB: STA $0042 ; orientationID = originalOrientationID;
88ED: RTS ; return;Coordinates
x, yand orientation of the current ID tetrimino stored respectively at the addresses $0040, $0041and $0042. The code uses a temporary variable to back up the orientation ID. Later, after changing the orientation, the code checks that all four squares are within the boundaries of the playing field and none of them overlaps the already lying squares (the verification code is located at the address
$948Bunder the code fragment shown above). If the new orientation is incorrect, then the original is restored, not allowing the player to rotate the figure. Counting from the cross, the NES controller has eight buttons, the status of which is represented by the address bit
$00B6.7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|
| A | B | Select | Start | Up | Way down | To the left | To the right |
For example, the
$00B6value will contain as $81long as the player holds A and Left. On the other hand,
$00B5reports when the buttons were pressed; the bits $00B5are true only during one iteration of the game cycle (1 rendered frame). The code uses $00B5to respond to presses A and B. Each of them must be released before being used again. $00B5and $00B6are mirrors $00F5and $00F6. The code in the following sections uses these addresses interchangeably.Create Tetrimino
The Nintendo Tetris game board consists of a matrix with 22 rows and 10 columns so that the top two rows are hidden from the player.

As shown in the code below, when creating a Tetrimino shape, it is always located in the coordinates of the
(5, 0)playing field.
Below is a 5 × 5 matrix overlaid on this point.98BA: LDA #$00
98BC: STA $00A4
98BE: STA $0045
98C0: STA $0041 ; Tetrimino Y = 0
98C2: LDA #$01
98C4: STA $0048
98C6: LDA #$05
98C8: STA $0040 ; Tetrimino X = 5
None of the creation matrices have squares above the starting point. That is, when creating a Tetrimino, all four of its squares are immediately visible to the player. However, if a player quickly rotates a piece before it has time to fall, part of the piece will be temporarily hidden in the first two lines of the playing field.
We usually think that the game ends when the heap reaches the top. But in fact it is not so. The game ends when it is no longer possible to create the next figure. That is, before the appearance of the figure, all four cells of the playing field should be free, corresponding to the positions of the squares created by Tetrimino. The figure may be blocked in place in such a way that some of its squares will appear in negatively numbered lines, and the game will not end; however, in Nintendo Tetris, negative lines are an abstraction that only applies to active Tetrimino. After the shape is blocked (becomes lying), only squares in lines from zero and more are written to the field. Conceptually, it turns out that negatively numbered lines are automatically cleared after blocking.
The visible area of the playing field 20 × 10 is stored at the address
$0400in a row order, each byte contains the value of the background tile. Empty cells are indicated by a tile $EF, a solid black square. When creating a shape, three lookup tables are used. If there is an arbitrary orientation ID, the table at the address
$9956gives us the orientation ID when creating the corresponding type of tetrimino.
Easier to show it in the table.9956: 02 02 02 02 ; Td
995A: 07 07 07 07 ; Jd
995E: 08 08 ; Zh
9960: 0A ; O
9961: 0B 0B ; Sh
9963: 0E 0E 0E 0E ; Ld
9967: 12 12 ; IhTu | Tr | Td | Tl | Jl | Ju | Jr | Jd | Zh | Zv | O | Sh | Sv | Lr | Ld | Ll | Lu | Iv | Ih |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Td | Td | Td | Td | Jd | Jd | Jd | Jd | Zh | Zh | O | Sh | Sh | Ld | Ld | Ld | Ld | Ih | Ih |
For example, all orientations J are attached to
Jd. The table at the address
$993Bcontains the tetrimino type for the specified orientation ID.
For clarity, I will show everything in tabular form.993B: 00 00 00 00 ; T
993F: 01 01 01 01 ; J
9943: 02 02 ; Z
9945: 03 ; O
9946: 04 04 ; S
9948: 05 05 05 05 ; L
994C: 06 06 ; ITu | Tr | Td | Tl | Jl | Ju | Jr | Jd | Zh | Zv | O | Sh | Sv | Lr | Ld | Ll | Lu | Iv | Ih |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
T | T | T | T | J | J | J | J | Z | Z | O | S | S | L | L | L | L | I | I |
We will look at the third lookup table in the next section.
Tetrimino Selection
The Nintendo Tetris as a pseudorandom number generator (PRNG) used a 16-bit linear feedback shift register (linear feedback shift register, LFSR) in Fibonacci configuration. 16-bit value is stored as big-endian by addresses
$0017- $0018. An arbitrary number is used as a Seed $8988.
Each subsequent pseudo-random number is generated as follows: the value is perceived as a 17-bit number, and the most significant bit is obtained by performing XOR for bits 1 and 9. Then the value is shifted to the right, discarding the least significant bit.80BC: LDX #$89
80BE: STX $0017
80C0: DEX
80C1: STX $0018
This process takes place at
$AB47.
Interestingly, the parameters of the subroutine shown above can be set so that the calling function can specify the width of the shift register and the address at which it can be found in memory. However, the same parameters are used everywhere, so we can assume that the developers somewhere have borrowed this code.
For those who want to further modify the algorithm, I wrote it in Java.AB47: LDA $00,X
AB49: AND #$02
AB4B: STA $0000 ; extract bit 1
AB4D: LDA $01,X
AB4F: AND #$02 ; extract bit 9
AB51: EOR $0000
AB53: CLC
AB54: BEQ $AB57
AB56: SEC ; XOR bits 1 and 9 together
AB57: ROR $00,X
AB59: INX
AB5A: DEY ; right shift
AB5B: BNE $AB57 ; shifting in the XORed value
AB5D: RTS ; returnintgenerateNextPseudorandomNumber(int value){
int bit1 = (value >> 1) & 1;
int bit9 = (value >> 9) & 1;
int leftmostBit = bit1 ^ bit9;
return (leftmostBit << 15) | (value >> 1);
}And all this code can be pressed down to one line.
intgenerateNextPseudorandomNumber(int value){
return ((((value >> 9) & 1) ^ ((value >> 1) & 1)) << 15) | (value >> 1);
}This PRNG continuously and deterministically generates 32,767 unique values, starting each cycle from the initial seed. This is one less than half of the possible numbers that can fit in a register, and any value in this set can be used as a seed. Many of the values outside the set create a chain that will eventually lead to a number from the set. However, some seed numbers result in an infinite sequence of zeros.
To estimate the performance of this PRNG roughly, I generated a graphical representation of the values it creates, based on a sentence with RANDOM.ORG .

When creating an image, PRNG was used as a pseudo-random number generator, rather than 16-bit integers. Each pixel is colored based on the value of bit 0. The image has a size of 128 × 256, that is, it covers the entire sequence.
Except for the barely noticeable stripes on the top and left sides, it looks random. No obvious patterns appear.
After launching, the PRNG constantly shuffles the register, triggering at least once a frame. This does not happen not only on the splash screen and menu screens, but also when tetrimino drops between the figure creation operations. That is, the figure appearing next depends on the number of frames taken by the player to place the figure. In fact, the game relies on the randomness of the actions of the person interacting with it.
During the creation of the figure, the code at the address
$9907that selects the type of the new figure is executed .
The address stores the number of figures created with the power. The increment of the counter is performed by the first line of the subroutine, and since it is a single-byte counter, it returns to zero after every 256 figures. Since the counter is not reset between games, the history of previous games affects the shape selection process. This is another way the game uses the player as a source of randomness.
The subroutine converts the most significant byte of a pseudo-random number ( ) into a Tetrimino type and uses it as an index of the table located at the address to convert the type to the shape creation ID of the orientation.9907: INC $001A ; spawnCount++;
9909: LDA $0017 ; index = high byte of randomValue;
990B: CLC
990C: ADC $001A ; index += spawnCount;
990E: AND #$07 ; index &= 7;
9910: CMP #$07 ; if (index == 7) {
9912: BEQ $991C ; goto invalidIndex;
; }
9914: TAX
9915: LDA $994E,X ; newSpawnID = spawnTable[index];
9918: CMP $0019 ; if (newSpawnID != spawnID) {
991A: BNE $9938 ; goto useNewSpawnID;
; }
invalidIndex:
991C: LDX #$17
991E: LDY #$02
9920: JSR $AB47 ; randomValue = generateNextPseudorandomNumber(randomValue);
9923: LDA $0017 ; index = high byte of randomValue;
9925: AND #$07 ; index &= 7;
9927: CLC
9928: ADC $0019 ; index += spawnID;
992A: CMP #$07
992C: BCC $9934
992E: SEC
992F: SBC #$07
9931: JMP $992A ; index %= 7;
9934: TAX
9935: LDA $994E,X ; newSpawnID = spawnTable[index];
useNewSpawnID:
9938: STA $0019 ; spawnID = newSpawnID;
993A: RTS ; return;$001A$0017$994E994E: 02 ; Td
994F: 07 ; Jd
9950: 08 ; Zh
9951: 0A ; O
9952: 0B ; Sh
9953: 0E ; Ld
9954: 12 ; IhAt the first stage of the conversion, the counter of the created figures is added to the upper byte. Then a mask is applied to save only the lower 3 bits. If the result is not 7, then this is the correct type of tetrimino, and if it is not the same as the previous selected figure, then the number is used as an index in the shape creation table. Otherwise, the next pseudo-random number is generated and a mask is applied to obtain the lower 3 bits of the upper byte, and then the previous shape creation orientation ID is added. Finally, a modular operation is performed to obtain the correct type of tetrimino, which is used as an index in the shape creation table.
Since the processor does not support division with remainder, this operator is emulated by repeatedly subtracting 7, until the result is less than 7. Division with remainder is applied to the sum of the upper byte with the mask and the previous ID of creating the shape. The maximum value of this sum is equal to 25. That is, in order to reduce it to the remainder of 4, only 3 iterations are required.
At the beginning of each game, the shape creation ID orientation (
$0019) is initialized with the value Tu( $00). This value can potentially be used at the address $9928at the time of the first shape creation. When used in the sum of the previous ID, the orientation of the shape creation, and not the previous type, Tetrimino adds distortion, because the values of the orientation ID are not evenly distributed. This is shown in the table:
| $ 00 | $02 | $07 | $08 | $0A | $0B | $0E | $12 |
|---|---|---|---|---|---|---|---|
| 0 | 2 | 0 | one | 3 | four | 0 | four |
| one | 3 | one | 2 | four | five | one | five |
| 2 | four | 2 | 3 | five | 6 | 2 | 6 |
| 3 | five | 3 | four | 6 | 0 | 3 | 0 |
| four | 6 | four | five | 0 | one | four | one |
| five | 0 | five | 6 | one | 2 | five | 2 |
| 6 | one | 6 | 0 | 2 | 3 | 6 | 3 |
| 7 | 2 | 0 | one | 3 | four | 0 | four |
Each cell contains the type of tetrimino, calculated by adding the orientation ID of the created figure (column) to the 3-bit value (line), and then applying the remainder of the division by 7 to the sum. Each line contains duplicates because
$07and $0Eevenly divide by 7, a $0Band $12have a common residue. Lines 0 and 7 are the same, because they are at a distance of 7. There are 56 possible input combinations, and if the resulting types are evenly distributed tetrimino, then we can expect that in the table shown above each type should appear exactly 8 times. But as shown below, it is not.
| Type of | Frequency |
|---|---|
| T | 9 |
| J | eight |
| Z | eight |
| O | eight |
| S | 9 |
| L | 7 |
| I | 7 |
T and S appear more often, and L and I - less. But skewed code using orientation ID is not executed every time a subroutine is called.
Suppose that a PRNG does create a sequence of uniformly distributed statistical independent values. In fact, this is a fair assumption, considering how the game tries to get the correct chance from the player’s actions. Adding the number of created figures to the address
$990Cwill not affect the distribution, because between calls the number increases evenly. Using a bitmask at an address is $990Esimilar to applying division by 8 with a remainder, which also does not affect the distribution. Therefore, the address check $9910goes to invalidIndex1/8 of all cases. And the probability of hitting when checking at$9918where the newly selected figure is compared with the previous figure is 7/8, with a probability of coincidence of 1/7. This means that there is an additional chance to 7/8 × 1/7 = 1/8be in invalidIndex. In general, there is a probability of 25% use of the code with a skew and a probability of 75% of using the code that selects tetrimino evenly. In a set of 224 created tetrimino, the expectation is 32 instances for each type. But in fact, the code creates the following distribution:
| Type of | Frequency |
|---|---|
| T | 33 |
| J | 32 |
| Z | 32 |
| O | 32 |
| S | 33 |
| L | 31 |
| I | 31 |
That is, clearing 90 lines and reaching level 9, the player will receive one extra T and S and one less L and I than statistically expected.
Tetriminos are selected with the following probabilities:
| Type of | Probability |
|---|---|
| T | 14.73% |
| J | 14.29% |
| Z | 14.29% |
| O | 14.29% |
| S | 14.73% |
| L | 13.84% |
| I | 13.84% |
It seems that in the statement that the “long stick” I never appears when it is needed, there is part of the truth (at least for Nintendo Tetris).
Tetrimino shift
Nintendo Tetris uses Delayed Auto Shift (DAS). Pressing Left or Right instantly moves tetrimino one cell horizontally. While holding one of these directional buttons causes the game to automatically move the piece every 6 frames with an initial delay of 16 frames.
This type of horizontal movement is controlled by the code at
$89AE.
As in the rotation code, a temporary variable is used here to back up the coordinates in case the new position is wrong.
Notice that the check makes it difficult to move the piece while the player presses "Down".89AE: LDA $0040
89B0: STA $00AE ; originalX = tetriminoX;
89B2: LDA $00B6 ; if (pressing down) {
89B4: AND #$04 ; return;
89B6: BNE $8A09 ; }
89B8: LDA $00B5 ; if (just pressed left/right) {
89BA: AND #$03 ; goto resetAutorepeatX;
89BC: BNE $89D3 ; }
89BE: LDA $00B6 ; if (not pressing left/right) {
89C0: AND #$03 ; return;
89C2: BEQ $8A09 ; }
89C4: INC $0046 ; autorepeatX++;
89C6: LDA $0046 ; if (autorepeatX < 16) {
89C8: CMP #$10 ; return;
89CA: BMI $8A09 ; }
89CC: LDA #$0A
89CE: STA $0046 ; autorepeatX = 10;
89D0: JMP $89D7 ; goto buttonHeldDown;
resetAutorepeatX:
89D3: LDA #$00
89D5: STA $0046 ; autorepeatX = 0;
buttonHeldDown:
89D7: LDA $00B6 ; if (not pressing right) {
89D9: AND #$01 ; goto notPressingRight;
89DB: BEQ $89EC ; }
89DD: INC $0040 ; tetriminoX++;
89DF: JSR $948B ; if (new position not valid) {
89E2: BNE $8A01 ; goto restoreX;
; }
89E4: LDA #$03
89E6: STA $06F1 ; play shift sound effect;
89E9: JMP $8A09 ; return;
notPressingRight:
89EC: LDA $00B6 ; if (not pressing left) {
89EE: AND #$02 ; return;
89F0: BEQ $8A09 ; }
89F2: DEC $0040 ; tetriminoX--;
89F4: JSR $948B ; if (new position not valid) {
89F7: BNE $8A01 ; goto restoreX;
; }
89F9: LDA #$03
89FB: STA $06F1 ; play shift sound effect;
89FE: JMP $8A09 ; return;
restoreX:
8A01: LDA $00AE
8A03: STA $0040 ; tetriminoX = originalX;
8A05: LDA #$10
8A07: STA $0046 ; autorepeatX = 16;
8A09: RTS ; return;xTetrimino toss
Automatic descent speed is a function of the level number. Speeds are encoded as the number of rendered frames per descent in the table located at
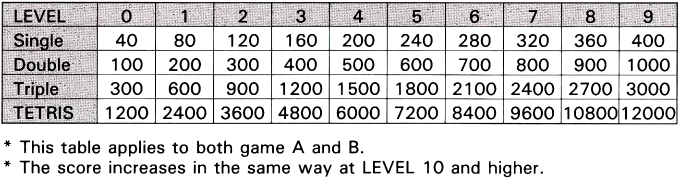
$898E. Since NES operates at 60.0988 frames / s, it is possible to calculate the period between descents and speed.| Level | Frames on the descent | Period (c / down) | Speed (cells / s) |
|---|---|---|---|
| 0 | 48 | .799 | 1.25 |
| one | 43 | .715 | 1.40 |
| 2 | 38 | .632 | 1.58 |
| 3 | 33 | .549 | 1.82 |
| four | 28 | .466 | 2.15 |
| five | 23 | .383 | 2.61 |
| 6 | 18 | .300 | 3.34 |
| 7 | 13 | .216 | 4.62 |
| eight | eight | .133 | 7.51 |
| 9 | 6 | .100 | 10.02 |
| 10–12 | five | .083 | 12.02 |
| 13–15 | four | .067 | 15.05 |
| 16-18 | 3 | .050 | 20.03 |
| 19–28 | 2 | .033 | 30.05 |
| 29+ | one | .017 | 60.10 |
There are 30 entries in the table. After level 29, the value of frames per descent is always 1. The
integer number of frames per descent is not a particularly detailed way of describing speed. As shown in the graph below, the rate increases exponentially with each level. In fact, level 29 is twice as fast as level 28.

At 1 frame / descent, the player has no more than 1/3 of a second to position the piece before it starts moving. At this speed of descent, DAS does not allow the figure to reach the edges of the playing field before blocking in place, which means for most people a quick end to the game. However, some players, in particular, Toru Akerlund , managed to defeat DAS with a quick vibration of the cross buttons (
D-pad). In the shift code shown above, it can be seen that while the horizontal direction button is released through the frame, it is possible to shift tetrimino at levels 29 and above with half the frequency. This is a theoretical maximum, but any thumb vibration above 3.75 taps can defeat an initial delay of 16 frames.If the automatic and player controlled descent (by pressing "Down") coincide and occur in one frame, the effect does not add up. Either or both of these events cause the shape to drop down exactly one cell in this frame.
The descent control logic is located at
$8914.
The table of frames for descent is below the mark . As stated above, at level 29 and above, the rate is always 1 descent / frame. (address ) starts the descent when it reaches ( ). The increment is performed at an address outside of this code fragment. With automatic or controlled descent, it is reset to 0. The
variable ( ) is initialized with the value (at the address8914: LDA $004E ; if (autorepeatY > 0) {
8916: BPL $8922 ; goto autorepeating;
; } else if (autorepeatY == 0) {
; goto playing;
; }
; game just started
; initial Tetrimino hanging at spawn point
8918: LDA $00B5 ; if (not just pressed down) {
891A: AND #$04 ; goto incrementAutorepeatY;
891C: BEQ $8989 ; }
; player just pressed down ending startup delay
891E: LDA #$00
8920: STA $004E ; autorepeatY = 0;
8922: BNE $8939
playing:
8924: LDA $00B6 ; if (left or right pressed) {
8926: AND #$03 ; goto lookupDropSpeed;
8928: BNE $8973 ; }
; left/right not pressed
892A: LDA $00B5
892C: AND #$0F ; if (not just pressed only down) {
892E: CMP #$04 ; goto lookupDropSpeed;
8930: BNE $8973 ; }
; player exclusively just presssed down
8932: LDA #$01
8934: STA $004E ; autorepeatY = 1;
8936: JMP $8973 ; goto lookupDropSpeed;
autorepeating:
8939: LDA $00B6
893B: AND #$0F ; if (down pressed and not left/right) {
893D: CMP #$04 ; goto downPressed;
893F: BEQ $894A ; }
; down released
8941: LDA #$00
8943: STA $004E ; autorepeatY = 0
8945: STA $004F ; holdDownPoints = 0
8947: JMP $8973 ; goto lookupDropSpeed;
downPressed:
894A: INC $004E ; autorepeatY++;
894C: LDA $004E
894E: CMP #$03 ; if (autorepeatY < 3) {
8950: BCC $8973 ; goto lookupDropSpeed;
; }
8952: LDA #$01
8954: STA $004E ; autorepeatY = 1;
8956: INC $004F ; holdDownPoints++;
drop:
8958: LDA #$00
895A: STA $0045 ; fallTimer = 0;
895C: LDA $0041
895E: STA $00AE ; originalY = tetriminoY;
8960: INC $0041 ; tetriminoY++;
8962: JSR $948B ; if (new position valid) {
8965: BEQ $8972 ; return;
; }
; the piece is locked
8967: LDA $00AE
8969: STA $0041 ; tetriminoY = originalY;
896B: LDA #$02
896D: STA $0048 ; playState = UPDATE_PLAYFIELD;
896F: JSR $9CAF ; updatePlayfield();
8972: RTS ; return;
lookupDropSpeed:
8973: LDA #$01 ; tempSpeed = 1;
8975: LDX $0044 ; if (level >= 29) {
8977: CPX #$1D ; goto noTableLookup;
8979: BCS $897E ; }
897B: LDA $898E,X ; tempSpeed = framesPerDropTable[level];
noTableLookup:
897E: STA $00AF ; dropSpeed = tempSpeed;
8980: LDA $0045 ; if (fallTimer >= dropSpeed) {
8982: CMP $00AF ; goto drop;
8984: BPL $8958 ; }
8986: JMP $8972 ; return;
incrementAutorepeatY:
8989: INC $004E ; autorepeatY++;
898B: JMP $8972 ; return;lookupDropSpeedfallTimer$0045dropSpeed$00AFfallTimer$8892autorepeatY$004E$0A$8739), which is interpreted as −96. The condition at the very beginning causes an initial delay. The very first tetrimino remains exposed in the air at the point of creation until autorepeatYit rises to 0, which takes 1.6 seconds. However, when you press "Down" in this phase, it is autorepeatYinstantly assigned 0. It is interesting that you can move and rotate the figure in this phase of the initial delay, without canceling it. The increment
autorepeatYis performed while holding down. When it reaches 3, a man-controlled descent occurs (“soft” descent) and is autorepeatYassigned 1. Therefore, the initial soft descent requires 3 frames, but then it repeats in each frame. In addition, it
autorepeatYincreases from 0 to 1 only when the game recognizes that the player has just pressed "Down" (at$00B5), but does not recognize holding down. This is important because it is autorepeatYreset to 0 when creating tetrimino (at $98E8), which creates an important feature: if the player himself lowers the figure and it is blocked, and he continues to press "Down" when creating the next figure, which often occurs at high levels, This will not lead to a soft descent of a new figure. To make it happen, the player must release the "Down", and then press the button again. Potentially soft descent can increase the number of points.
holdDownPoints( $004F) increases with each descent, but when you press "Down" is reset to 0. Therefore, for a set of points it is necessary to lower the tetrimino into the lock by a soft descent. Short-term soft descent, which can occur in the way of the figure, does not affect the glasses. The account is updated at$9BFE, and is holdDownPointsreset to 0 shortly thereafter, at $9C2F. A check that prevents a player from performing a soft descent during a horizontal shift of a figure complicates the set of points. It means that the last move before blocking a piece in place must be “Down”.
When a descent occurs,
tetriminoY( $0041) is copied to originalY( $00AE). If the new position created by the increment tetriminoYturns out to be wrong (that is, the figure is either pushed through the floor of the playing field, or superimposed on the squares already lying), then the tetrimino remains in the previous position. In this case, is restoredtetriminoYand the figure is considered blocked. This means that the delay before blocking (the maximum number of frames that a tetrimino expects, keeping itself in the air before blocking) is equal to the delay of descent. Hard descent (instant figure drop) is not supported in Nintendo Tetris.
Sliding and scrolling
The Nintendo Tetris handbook has an illustrated example of how to do a slip:

Sliding consists of shifting along the surface of other pieces or along the floor of the playing field. It is usually used to stick a piece under a hanging square. The slide can be performed until the drop timer reaches the speed of descent, after which the figure will be locked in place. Below is an animated example.

On the other hand, scrolling allows you to stick figures into spaces that cannot be reached in any other way (see below).

Like sliding, scrolling is impossible without blocking delay. But beyond that, scrolling exploits the way in which the game manipulates figures. Before moving or rotating the figure, the game checks that after changing the position, all the squares of tetrimino will be in empty cells within the boundaries of the playing field. Such a check, as shown below, does not prevent rotation through the nearest filled blocks. As stated in the “Tetrimino Description” section, each row of the orientation table contains 12 bytes; therefore, the index in this table is calculated by multiplying the active orientation Tetrimino ID by 12. As shown below, all multiplications in the subroutine are performed using shifts and addition.
948B: LDA $0041
948D: ASL
948E: STA $00A8
9490: ASL
9491: ASL
9492: CLC
9493: ADC $00A8
9495: ADC $0040
9497: STA $00A8
9499: LDA $0042
949B: ASL
949C: ASL
949D: STA $00A9
949F: ASL
94A0: CLC
94A1: ADC $00A9
94A3: TAX ; index = 12 * orientationID;
94A4: LDY #$00
94A6: LDA #$04
94A8: STA $00AA ; for(i = 0; i < 4; i++) {
94AA: LDA $8A9C,X ; squareY = orientationTable[index];
94AD: CLC
94AE: ADC $0041 ; cellY = squareY + tetriminoY;
94B0: ADC #$02 ; if (cellY < -2 || cellY >= 20) {
94B2: CMP #$16 ; return false;
94B4: BCS $94E9 ; }
94B6: LDA $8A9C,X
94B9: ASL
94BA: STA $00AB
94BC: ASL
94BD: ASL
94BE: CLC
94BF: ADC $00AB
94C1: CLC
94C2: ADC $00A8
94C4: STA $00AD
94C6: INX
94C7: INX ; index += 2;
94C8: LDA $8A9C,X ; squareX = orientationTable[index];
94CB: CLC
94CC: ADC $00AD
94CE: TAY ; cellX = squareX + tetriminoX;
94CF: LDA ($B8),Y ; if (playfield[10 * cellY + cellX] != EMPTY_TILE) {
94D1: CMP #$EF ; return false;
94D3: BCC $94E9 ; }
94D5: LDA $8A9C,X
94D8: CLC
94D9: ADC $0040 ; if (cellX < 0 || cellX >= 10) {
94DB: CMP #$0A ; return false;
94DD: BCS $94E9 ; }
94DF: INX ; index++;
94E0: DEC $00AA
94E2: BNE $94AA ; }
94E4: LDA #$00
94E6: STA $00A8
94E8: RTS ; return true;
94E9: LDA #$FF
94EB: STA $00A8
94ED: RTSindex = (orientationID << 3) + (orientationID << 2); // index = 8 * orientationID + 4 * orientationID;
(cellY << 3) + (cellY << 1) // 8 * cellY + 2 * cellYEach iteration of the cycle shifts the position of the tetrimino by the relative coordinates of one of the squares from the orientation table in order to obtain the corresponding position of the cell on the playing field. She then checks that the coordinates of the cell are within the boundaries of the playing field, and that the cell itself is empty.
The comments describe more clearly the way in which line spacing checks are performed. In addition to the cells in the visible lines, the code considers two hidden lines above the playing field as the legal positions of the squares without using the compound condition. This works because in the additional code the negative numbers represented by single-byte variables are equivalent to values greater than 127. In this case, the minimum value is −2, which is stored as
94AA: LDA $8A9C,X ; squareY = orientationTable[index];
94AD: CLC
94AE: ADC $0041 ; cellY = squareY + tetriminoY;
94B0: ADC #$02 ; if (cellY + 2 >= 22) {
94B2: CMP #$16 ; return false;
94B4: BCS $94E9 ; }cellY$FE(254 in decimal). The playing field index is the amount
cellYmultiplied by 10 and cellX. However, when cellYequal to −1 ( $FF= 255) or −2 ( $FE= 254), the result is −10 ( $F6= 246) and −20 ( $EC= 236). Being in the interval, it cellXcan be no more than 9, which gives a maximum index of 246 + 9 = 255, and this is much further than the end of the playing field. However, the game initializes $0400- $04FFwith a value $EF(empty tile), creating another 56 additional bytes of empty space. It is strange that the interval check
cellXperformed after examining the cell of the playing field. But it works correctly in any order. In addition, the interval check avoids a compound condition, as indicated below in the commentary.
The scrolling examples shown below are possible due to the way this code checks positions.94D5: LDA $8A9C,X
94D8: CLC
94D9: ADC $0040 ; if (cellX >= 10) {
94DB: CMP #$0A ; return false;
94DD: BCS $94E9 ; }

As shown below, you can even perform a slide with scrolling.

The AI uses all the movement capabilities available in Nintendo Tetris, including sliding and scrolling.
Level 30 and above
After reaching level 30 it seems that the level is reset to zero.

But level 31 shows that something else is happening:

The displayed level values are located in the table at
$96B8. 96B8: 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29As shown below, the pattern table is ordered in such a way that tiles with
$00to $0Fare glyphs for characters from 0to F. This means that when displaying a digit of a decimal or hexadecimal number, the value of the digit itself is used as the index of the pattern table. In our case, the values of the levels are stored as a binary-decimal code (binary-coded decimal, BCD); each nibble of each byte in the sequence is a tile value.
Unfortunately, it seems that the game designers assumed that no one would pass level 29, and therefore decided to insert only 30 records into the table. Strange display values are different bytes after the table. To indicate the level number, only one byte is used (at the address
$0044), which is why the game slowly cycles around the values shown below.00 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
0 | 00 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 |
1 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 00 | 0A |
2 | 14 | 1E | 28 | 32 | 3C | 46 | 50 | 5A | 64 | 6E | 78 | 82 | 8C | 96 | A0 | AA |
3 | B4 | BE | C6 | 20 | E6 | 20 | 06 | 21 | 26 | 21 | 46 | 21 | 66 | 21 | 86 | 21 |
4 | A6 | 21 | C6 | 21 | E6 | 21 | 06 | 22 | 26 | 22 | 46 | 22 | 66 | 22 | 86 | 22 |
5 | A6 | 22 | C6 | 22 | E6 | 22 | 06 | 23 | 26 | 23 | 85 | A8 | 29 | F0 | 4A | 4A |
6 | 4A | 4A | 8D | 07 | 20 | A5 | A8 | 29 | 0F | 8D | 07 | 20 | 60 | A6 | 49 | E0 |
7 | 15 | 10 | 53 | BD | D6 | 96 | A8 | 8A | 0A | AA | E8 | BD | EA | 96 | 8D | 06 |
8 | 20 | CA | A5 | BE | C9 | 01 | F0 | 1E | A5 | B9 | C9 | 05 | F0 | 0C | BD | EA |
9 | 96 | 38 | E9 | 02 | 8D | 06 | 20 | 4C | 67 | 97 | BD | EA | 96 | 18 | 69 | 0C |
A | 8D | 06 | 20 | 4C | 67 | 97 | BD | EA | 96 | 18 | 69 | 06 | 8D | 06 | 20 | A2 |
B | 0A | B1 | B8 | 8D | 07 | 20 | C8 | CA | D0 | F7 | E6 | 49 | A5 | 49 | C9 | 14 |
C | 30 | 04 | A9 | 20 | 85 | 49 | 60 | A5 | B1 | 29 | 03 | D0 | 78 | A9 | 00 | 85 |
D | AA | A6 | AA | B5 | 4A | F0 | 5C | 0A | A8 | B9 | EA | 96 | 85 | A8 | A5 | BE |
E | C9 | 01 | D0 | 0A | A5 | A8 | 18 | 69 | 06 | 85 | A8 | 4C | BD | 97 | A5 | B9 |
F | C9 | 04 | D0 | 0A | A5 | A8 | 38 | E9 | 02 | 85 | A8 | 4C | BD | 97 | A5 | A8 |
The first 20 ordinal values are actually another table in which the offsets on the playing field for each of the 20 rows are stored. Since the playing field starts with and each row contains 10 cells, the address of an arbitrary cell is: Given that the processor does not directly multiply, this lookup table provides an extremely fast way to get the piece. The corresponding table is the next 40 bytes. It contains 20 addresses in little endian format for a nametable 0 (a VRAM memory area containing background tile values). They are pointers to the playing field offset lines on . The remaining bytes, of which the displayed level values are composed, are instructions.
96D6: 00 ; 0
96D7: 0A ; 10
96D8: 14 ; 20
96D9: 1E ; 30
96DA: 28 ; 40
96DB: 32 ; 50
96DC: 3C ; 60
96DD: 46 ; 70
96DE: 50 ; 80
96DF: 5A ; 90
96E0: 64 ; 100
96E1: 6E ; 110
96E2: 78 ; 120
96E3: 82 ; 130
96E4: 8C ; 140
96E5: 96 ; 150
96E6: A0 ; 160
96E7: AA ; 170
96E8: B4 ; 180
96E9: BE ; 190$0400$0400 + 10 * y + x$0400 + [$96D6 + y] + x$06Rows and statistics
The number of filled rows and tetrimino statistics occupy 2 bytes each at the following addresses.
| Addresses | amount |
|---|---|
0050-0051 | Rows |
03F0-03F1 | T |
03F2-03F3 | J |
03F4-03F5 | Z |
03F6-03F7 | O |
03F8-03F9 | S |
03FA-03FB | L |
03FC-03FD | I |
Essentially, these values are stored as 16-bit packed BCD little endian. For example, below is the number of rows equal to 123. The bytes are counted from right to left for the decimal digits to go in order.

However, the game designers assumed that none of the values would be greater than 999. Therefore, the display logic correctly processes the first byte as a packed BCD, where each nibble is used as a tile value. But the entire second byte is actually used as the top decimal digit. When the bottom digits go from
99to 00the usual increment of the second byte occurs. As a result, the second byte cycles through all 256 tiles. Below is an example of this.
After the row is cleared, the following code is executed to increment the number of rows. Checks are performed for the middle and lower digits so that they remain in the range from 0 to 9. But the upper digit can be increased indefinitely. If after the increment of the number of rows, the lower digit is 0, then this means that the player has just completed a set of 10 rows and you need to increase the level number. As can be seen from the code below, an additional check is performed before the increment of the level. The second check is related to the selected initial level. To go to any level , regardless of the initial level, the player must clear
9BA8: INC $0050 ; increment middle-lowest digit pair
9BAA: LDA $0050
9BAC: AND #$0F
9BAE: CMP #$0A ; if (lowest digit > 9) {
9BB0: BMI $9BC7
9BB2: LDA $0050
9BB4: CLC
9BB5: ADC #$06 ; set lowest digit to 0, increment middle digit
9BB7: STA $0050
9BB9: AND #$F0
9BBB: CMP #$A0 ; if (middle digit > 9) {
9BBD: BCC $9BC7
9BBF: LDA $0050
9BC1: AND #$0F
9BC3: STA $0050 ; set middle digit to 0
9BC5: INC $0051 ; increment highest digit
; }
; }9BC7: LDA $0050
9BC9: AND #$0F
9BCB: BNE $9BFB ; if (lowest digit == 0) {
9BCD: JMP $9BD0
9BD0: LDA $0051
9BD2: STA $00A9
9BD4: LDA $0050
9BD6: STA $00A8 ; copy digits from $0050-$0051 to $00A8-$00A9
9BD8: LSR $00A9
9BDA: ROR $00A8
9BDC: LSR $00A9
9BDE: ROR $00A8
9BE0: LSR $00A9
9BE2: ROR $00A8 ; treat $00A8-$00A9 as a 16-bit packed BCD value
9BE4: LSR $00A9 ; and right-shift it 4 times
9BE6: ROR $00A8 ; this leaves the highest and middle digits in $00A8
9BE8: LDA $0044
9BEA: CMP $00A8 ; if (level < [$00A8]) {
9BEC: BPL $9BFB
9BEE: INC $0044 ; increment level
; }
; }X10Xlines. For example, if a player starts from level 5, he will remain on him until he has cleared 60 lines, after which he will go to level 6. After that, every additional 10 lines will result in an increment of level numbers. To perform this check, the value of the filled rows is copied from
$0050- $0051to $00A8- $00A9. Then the copy is shifted 4 times to the right, which for a packed BCD is similar to division by 10. The youngest decimal digit is discarded, and the highest and middle digits are shifted by one position, as a result becoming nibbles $00A8.
However, at the address
$9BEAthe level number is directly compared with the BCD's packed value $00A8. There is no search in the table for converting the BCD value to decimal, and this is an obvious error. For example, in the picture shown above, the level number should be compared with $12(18 in decimal), and not with 12. Therefore, if a player decides to start at level 17, then the level will actually go to 120 rows, because 18 is greater than 17. The table shows the expected number of rows required for the transition at each initial level. It is compared with the fact that because of the bug is actually happening.
Начальный уровень | 0 | one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten | eleven | 12 | 13 | 14 | 15 | sixteen | 17 | 18 | nineteen |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Ожидаемое количество рядов | ten | 20 | thirty | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
Количество рядов на самом деле | ten | 20 | thirty | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 110 | 120 | 130 | 140 |
The expected number coincides with the true for the initial levels of 0–9. In fact, the coincidence for entry level 9 is random; 10–15 also moves to the next level with 100 rows, because it
$10is 16 in decimal form. The largest difference between the expected and actual is 60 rows. I suspect that the bug is related to design changes in the later stages of development. Look at the menu screen, which allows the player to choose the starting level.

There is no explanation of how to start with levels above 9. But in the Nintendo Tetris guide booklet this secret is revealed:

It seems that this hidden feature was invented at the last moment. Perhaps it was added very close to the release date, which made it impossible to fully test it.
In fact, the verification of the initial series contains a second error associated with the output of values for the interval. Below are the comments in the code that best explain what is happening at a low level. The comparison is performed by subtracting and checking the sign of the result. But the signed one-byte number is limited to the interval from −128 to 127. If the difference is less than −128, the number is transferred and the result becomes a positive number. This principle is explained in the comments to the code. When checking that the difference is in this interval, you need to take into account that the level number with increment to values greater than 255 performs a transfer to 0, and
9BE8: LDA $0044
9BEA: CMP $00A8 ; if (level - [$00A8] < 0) {
9BEC: BPL $9BFB
9BEE: INC $0044 ; increment level
; }9BE8: LDA $0044 ; difference = level - [$00A8];
9BEA: CMP $00A8 ; if (difference < 0 && difference >= -128) {
9BEC: BPL $9BFB
9BEE: INC $0044 ; increment level
; }$00A8can potentially contain any value, because its upper nibble is taken from $0051, the increment of which can occur indefinitely. These effects overlap, creating periods in which the level number erroneously remains unchanged. Periods occur at regular intervals of 2,900 rows, starting at 2,190 rows, and last for 800 rows. For example, from 2190 (
L90) to 2990 ( T90) the level remains equal to $DB( 96), as shown below.
The next period happens from 5090 to 5890, the level is constantly equal to
$AD( 06). In addition, during these periods the color palette also does not change.Coloring Tetrimino
At each level, tetrimino tiles are assigned 4 unique colors. Colors are taken from the table located at
$984C. Her records are reused every 10 levels.
From left to right: the columns of the table correspond to the black, white, blue and red areas of the image shown below.984C: 0F 30 21 12 ; level 0
9850: 0F 30 29 1A ; level 1
9854: 0F 30 24 14 ; level 2
9858: 0F 30 2A 12 ; level 3
985C: 0F 30 2B 15 ; level 4
9860: 0F 30 22 2B ; level 5
9864: 0F 30 00 16 ; level 6
9868: 0F 30 05 13 ; level 7
986C: 0F 30 16 12 ; level 8
9870: 0F 30 27 16 ; level 9
Values correspond to the NES color palette.

The first 2 colors of each record are always black and white. However, in fact, the first color is ignored; regardless of the value, it is considered to be a transparent color through which a solid black background peeps through.
Access to the color table is performed in the subroutine at
$9808.
The index of the color table is based on the level number divided by the remainder by 10. The cycle copies the record to the palette tables in the VRAM memory.
The division with the remainder is emulated by a constant subtraction of 10 until the result is less than 10. Below is shown the beginning of the subroutine with comments.9808: LDA $0064
980A: CMP #$0A
980C: BMI $9814
980E: SEC
980F: SBC #$0A
9811: JMP $980A ; index = levelNumber % 10;
9814: ASL
9815: ASL
9816: TAX ; index *= 4;
9817: LDA #$00
9819: STA $00A8 ; for(i = 0; i < 32; i += 16) {
981B: LDA #$3F
981D: STA $2006
9820: LDA #$08
9822: CLC
9823: ADC $00A8
9825: STA $2006 ; palette = $3F00 + i + 8;
9828: LDA $984C,X
982B: STA $2007 ; palette[0] = colorTable[index + 0];
982E: LDA $984D,X
9831: STA $2007 ; palette[1] = colorTable[index + 1];
9834: LDA $984E,X
9837: STA $2007 ; palette[2] = colorTable[index + 2];
983A: LDA $984F,X
983D: STA $2007 ; palette[3] = colorTable[index + 3];
9840: LDA $00A8
9842: CLC
9843: ADC #$10
9845: STA $00A8
9847: CMP #$20
9849: BNE $981B ; }
984B: RTS ; return;9808: LDA $0064 ; index = levelNumber;
980A: CMP #$0A ; while(index >= 10) {
980C: BMI $9814
980E: SEC
980F: SBC #$0A ; index -= 10;
9811: JMP $980A ; }However, as mentioned in the previous section, subtraction and branching based on the sign of the difference is used in comparison. A signed single-byte number is limited to an interval from −128 to 127. The updated comments below reflect this principle. The comments below are even more simplified. Such a formulation reveals an error in the code. The division operation with the remainder is completely skipped for levels from 138 and above. Instead, the index is assigned directly to the level number, which provides access to the bytes far beyond the end of the color table. As shown below, it can even lead to almost invisible tetrimino.
9808: LDA $0064 ; index = levelNumber;
; difference = index - 10;
980A: CMP #$0A ; while(difference >= 0 && difference <= 127) {
980C: BMI $9814
980E: SEC ; index -= 10;
980F: SBC #$0A ; difference = index - 10;
9811: JMP $980A ; }9808: LDA $0064 ; index = levelNumber;
980A: CMP #$0A ; while(index >= 10 && index <= 137) {
980C: BMI $9814
980E: SEC
980F: SBC #$0A ; index -= 10;
9811: JMP $980A ; }
Below are the colors of all 256 levels. The tiles are arranged in 10 columns to emphasize the cyclic use of the color table, broken at level 138. Rows and columns in the headers are indicated in decimal form.

After 255, the level number returns to 0.
In addition, as mentioned in the previous section, some levels do not change until 800 rows are removed. During these long levels of color remain unchanged.
Game mode
The game mode stored at the address
$00C0determines which of the various screens and menus is displayed to the user at the moment.| Value | Description |
|---|---|
00 | Legal Information Screen |
01 | Screen saver |
02 | Game Type Menu |
03 | Level and height menu |
04 | Game / screen records / ending / pause |
05 | Demo |
As shown above, the game has a cleverly written subroutine that performs the role of a switch statement using the little endian transition table, located immediately after the call. The list above shows the addresses of all game modes. Note that the “Game” and “Demo” modes use the same code. This routine never returns. Instead, the code uses the return address; usually it indicates the instruction immediately following the jump to the subroutine (minus 1 byte), but in this case it points to the jump table. The return address is removed from the stack and saved to - . After saving the jump table address, the code uses the value in register A as an index and performs the corresponding jump.
8161: LDA $00C0
8163: JSR $AC82 ; switch(gameMode) {
8166: 00 82 ; case 0: goto 8200; // Экран с юридической информацией
8168: 4F 82 ; case 1: goto 824F; // Экран заставки
816A: D1 82 ; case 2: goto 82D1; // Меню типа игры
816C: D7 83 ; case 3: goto 83D7; // Меню уровней и высоты
816E: 5D 81 ; case 4: goto 815D; // Игра / экран рекордов / концовка / пауза
8170: 5D 81 ; case 5: goto 815D; // Демо
; }$0000$0001AC82: ASL
AC83: TAY
AC84: INY
AC85: PLA
AC86: STA $0000
AC88: PLA ; pop return address off of stack
AC89: STA $0001 ; and store it at $0000-$0001
AC8B: LDA ($00),Y
AC8D: TAX
AC8E: INY
AC8F: LDA ($00),Y
AC91: STA $0001
AC93: STX $0000
AC95: JMP ($0000) ; goto Ath 16-bit address
; in table at [$0000-$0001]The code can use this switch-subroutine, as long as the indices are close to 0 and there are no gaps between possible cases or few of them.
Legal Information Screen
The game starts with a screen that shows legal notice.

At the bottom of the screen, Alexey Pajitnov is mentioned as an inventor, designer and programmer of the first Tetris. In 1984, while working as a computer developer at the Dorodnitsyn Computing Center (a leading research institute of the Russian Academy of Sciences in Moscow), he developed a prototype game for Electronics-60 (the Soviet clone DEC LSI-11 ). The prototype was developed for a green monochrome text mode, in which the squares are denoted by pairs of square brackets
[]. With the help of 16-year-old schoolboy Vadim Gerasimov and computer engineer Dmitry Pavlovsky a few days after the invention of the game, the prototype was ported to an IBM PC with MS DOS and Turbo Pascal. For two years, they improved the game together, adding features such as tetrimino colors, statistics and, more importantly, timing code and graphics that allowed the game to work on many PC models and clones. Unfortunately, due to the peculiarities of the Soviet Union of that time, their attempts to monetize the game were not crowned with success, and in the end they decided to share the PC version with their friends for free. From that moment on, Tetris began to spread around the country and beyond its borders, copied from a floppy disk to a floppy disk. But since the game was developed by employees of a state institution, the state was its owner, and in 1987 the organization responsible for the international trade in electronic technology took up licensing the game (ELorg)). The abbreviation V / O on the legal information screen can be abbreviated from Version Originale. Andromeda, a
British software development company, tried to get rights to Tetris and, before the deal was completed, slanted the game to other suppliers, for example, the British computer game publisher Mirrorsoft . Mirrorsoft, in turn, sublicensed it to Tengen , a subsidiary of Atari Games. Tengen granted Bullet-Proof Software the rights to develop games for computers and consoles in Japan, which resulted in Tetris for Nintendo Famicom . Below is his legal information screen.

Interestingly, in this version the schoolboy Vadim Gerasimov is called the original designer and programmer.
Trying to get the rights to the portable version for the upcoming Game Boy console, Nintendo used Bullet-Proof Software to make a successful deal directly with ELORG. In the process of concluding a deal, ELORG revised its contract with Andromeda, adding that Andromeda received rights only for games for computers and arcade machines. Because of this, Bullet-Proof Software had to pay ELORG license fees for all the cartridges sold to Famicom, because the rights it received from Tengen turned out to be fake. But thanks to reconciliation with Bullet-Proof Software's ELORG, we finally managed to get worldwide rights to console games for Nintendo.
Bullet-Proof Software sublicensed the rights to Nintendo portable games and together they developed Game Boy Tetris, which is reflected in the legal information screen shown below.

Having obtained worldwide rights to console games, Nintendo developed the Tetris version for NES, which we study in this article. Then Bullet-Proof Software sublicensed Nintendo's rights, which allowed it to continue selling cartridges for Famicom in Japan.
This was followed by a complex legal dispute. Both Nintendo and Tengen demanded that the opposing side stop producing and selling their version of the game. As a result, Nintendo won, and hundreds of thousands of Tengen Tetris cartridges were destroyed. The court’s verdict also prohibited several other companies like Mirrorsoft from creating console versions.
Pajitnov never received any deductions from ELORG or the Soviet state. However, in 1991 he moved to the USA and in 1996 with the support of the owner of Bullet-Proof SoftwareHenk Rogers co-founded The Tetris Company , which enabled him to profit from versions for mobile devices and modern consoles.
It is curious to look at the legal information screen as a window, giving an idea of the modest birth of the game and the ensuing battles for intellectual property rights, because for most players this screen is just an annoying obstacle, the disappearance of which seems to wait forever. The delay is set by two counters, sequentially performing a counting from 255 to 0. The first phase cannot be skipped, and the second is skipped by pressing the Start button. Therefore, the legal information screen is displayed for at least 4.25 seconds and not more than 8.5 seconds. However, I think that most of the players give up, stopping pressing Start during the first interval, and because of this it is waiting for complete completion.
The timing of the phases, as well as the rest of the game, is controlled by a nonmaskable interrupt handler called at the beginning of each vertical blanking interval — a short period of time between rendering television frames. That is, every 16.6393 milliseconds, normal program execution is interrupted by the following code. The handler starts by transferring the values of the main registers to the stack and retrieves them after completion in order not to interfere with the interrupted task. The call updates VRAM, transforming the description of the memory model into what is displayed on the screen. Next, the handler reduces the value of the legal information screen counter, if it is greater than zero. Call
8005: PHA
8006: TXA
8007: PHA
8008: TYA
8009: PHA ; save A, X, Y
800A: LDA #$00
800C: STA $00B3
800E: JSR $804B ; render();
8011: DEC $00C3 ; legalScreenCounter1--;
8013: LDA $00C3
8015: CMP #$FF ; if (legalScreenCounter1 < 0) {
8017: BNE $801B ; legalScreenCounter1 = 0;
8019: INC $00C3 ; }
801B: JSR $AB5E ; initializeOAM();
801E: LDA $00B1
8020: CLC
8021: ADC #$01
8023: STA $00B1
8025: LDA #$00
8027: ADC $00B2
8029: STA $00B2 ; frameCounter++;
802B: LDX #$17
802D: LDY #$02
802F: JSR $AB47 ; randomValue = generateNextPseudorandomNumber(randomValue);
8032: LDA #$00
8034: STA $00FD
8036: STA $2005 ; scrollX = 0;
8039: STA $00FC
803B: STA $2005 ; scrollY = 0;
803E: LDA #$01
8040: STA $0033 ; verticalBlankingInterval = true;
8042: JSR $9D51 ; pollControllerButtons();
8045: PLA
8046: TAY
8047: PLA
8048: TAX
8049: PLA ; restore A, X, Y
804A: RTI ; resume interrupted taskrender()initializeOAM()performs the step required by frame generation equipment. The handler continues to work by incrementing the frame counter — the 16-bit little endian value stored at $00B1— $00B2which it uses in different places for controlled timing. After that, the next pseudo-random number is generated; as mentioned above, this happens regardless of the mode at least once per frame. At the address, $8040the vertical blanking interval flag is set, indicating that a handler has just been executed. Finally, the controller buttons are polled; The behavior of this subroutine is described below in the “Demo” section. The flag is
verticalBlankingIntervalused by the subroutine discussed above. It continues until the execution of the interrupt handler begins.AA2F: JSR $E000 ; updateAudio();
AA32: LDA #$00
AA34: STA $0033 ; verticalBlankingInterval = false;
AA36: NOP
AA37: LDA $0033
AA39: BEQ $AA37 ; while(!verticalBlankingInterval) { }
AA3B: LDA #$FF
AA3D: LDX #$02
AA3F: LDY #$02
AA41: JSR $AC6A ; fill memory page 2 with all $FF's
AA44: RTS ; return;This blocking subroutine is used in two stages of legal information screen timings that are executed one after the other. The AI script on Lua bypasses this delay by assigning the value 0 to both counters.
8236: LDA #$FF
8238: JSR $A459
...
A459: STA $00C3 ; legalScreenCounter1 = 255;
A45B: JSR $AA2F ; do {
A45E: LDA $00C3 ; waitForVerticalBlankingInterval();
A460: BNE $A45B ; } while(legalScreenCounter1 > 0);
A462: RTS ; return;823B: LDA #$FF
823D: STA $00A8 ; legalScreenCounter2 = 255;
; do {
823F: LDA $00F5 ; if (just pressed Start) {
8241: CMP #$10 ; break;
8243: BEQ $824C ; }
8245: JSR $AA2F ; waitForVerticalBlankingInterval();
8248: DEC $00A8 ; legalScreenCounter2--;
824A: BNE $823F ; } while(legalScreenCounter2 > 0);
824C: INC $00C0 ; gameMode = TITLE_SCREEN;Demo
The demo shows approximately 80 seconds of pre-recorded gameplay. It does not just display the video file, but uses the same engine as in the game. During playback, two tables are used. The first one, located at the address
$DF00, contains the following creation sequence: Tetrimino: T J T S Z J T S Z J S Z L Z J T T S I T O J S Z L Z L I O L Z L I O J T S I T O JWhen creating a figure, it is either chosen randomly or read from a table, depending on the mode. Switching occurs at
$98EB.
The tetrimino type is extracted from bits 6, 5, and 4 of each byte. From time to time this operation gives us the value — the wrong type. However, the shape creation table ( ) used to convert the Tetrimino type to the orientation ID is actually located between two related tables:
Value98EB: LDA $00C0
98ED: CMP #$05
98EF: BNE $9903 ; if (gameMode == DEMO) {
98F1: LDX $00D3
98F3: INC $00D3
98F5: LDA $DF00,X ; value = demoTetriminoTypeTable[++demoIndex];
98F8: LSR
98F9: LSR
98FA: LSR
98FB: LSR
98FC: AND #$07
98FE: TAX ; tetriminoType = bits 6,5,4 of value;
98FF: LDA $994E,X
9902: RTS ; return spawnTable[tetriminoType];
; } else {
; pickRandomTetrimino();
; }$07$994E993B: 00 00 00 00 ; T
993F: 01 01 01 01 ; J
9943: 02 02 ; Z
9945: 03 ; O
9946: 04 04 ; S
9948: 05 05 05 05 ; L
994C: 06 06 ; I994E: 02 ; Td
994F: 07 ; Jd
9950: 08 ; Zh
9951: 0A ; O
9952: 0B ; Sh
9953: 0E ; Ld
9954: 12 ; Ih9956: 02 02 02 02 ; Td
995A: 07 07 07 07 ; Jd
995E: 08 08 ; Zh
9960: 0A ; O
9961: 0B 0B ; Sh
9963: 0E 0E 0E 0E ; Ld
9967: 12 12 ; Ih$07causes it to read past the end of the table, in the next one that gives Td( $02). Because of this effect, this scheme can give us an unlimited, but reproducible sequence of pseudo-random ID orientations of the created figures. The code will work because any arbitrary address in a varying sequence of bytes does not allow us to determine where the table ends. In fact, the sequence at an address
$DF00can be part of something completely unrelated to it, especially considering that the assignment of the remaining 5 non-zero bits is not clear, and the generated sequence exhibits repeatability. During the initialization of the demo mode, the index of the table (
$00D3) is reset to the address $872B.The second demo table contains a record of gamepad buttons, encoded in pairs of bytes. The bits of the first byte correspond to the buttons.
7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|
| A | B | Select | Start | Up | Way down | To the left | To the right |
The second byte stores the number of frames during which the combination of buttons is pressed.
The table takes the address
$DD00- $DEFFand consists of 256 pairs. It is accessed by the subroutine at $9D5B.
Since the table of demo buttons has a length of 512 bytes, a two-byte index is required to access it. The index is stored as little endian to the addresses - . It is initialized with the value of the address of the table , and its increment is executed by the following code.
The programmers left in the code the player's input processing, which allows us to look at the development process and replace the demo with another entry. Demo recording mode is activated when a value is assigned9D5B: LDA $00D0 ; if (recording mode) {
9D5D: CMP #$FF ; goto recording;
9D5F: BEQ $9DB0 ; }
9D61: JSR $AB9D ; pollController();
9D64: LDA $00F5 ; if (start button pressed) {
9D66: CMP #$10 ; goto startButtonPressed;
9D68: BEQ $9DA3 ; }
9D6A: LDA $00CF ; if (repeats == 0) {
9D6C: BEQ $9D73 ; goto finishedMove;
; } else {
9D6E: DEC $00CF ; repeats--;
9D70: JMP $9D9A ; goto moveInProgress;
; }
finishedMove:
9D73: LDX #$00
9D75: LDA ($D1,X)
9D77: STA $00A8 ; buttons = demoButtonsTable[index];
9D79: JSR $9DE8 ; index++;
9D7C: LDA $00CE
9D7E: EOR $00A8
9D80: AND $00A8
9D82: STA $00F5 ; setNewlyPressedButtons(difference between heldButtons and buttons);
9D84: LDA $00A8
9D86: STA $00CE ; heldButtons = buttons;
9D88: LDX #$00
9D8A: LDA ($D1,X)
9D8C: STA $00CF ; repeats = demoButtonsTable[index];
9D8E: JSR $9DE8 ; index++;
9D91: LDA $00D2 ; if (reached end of demo table) {
9D93: CMP #$DF ; return;
9D95: BEQ $9DA2 ; }
9D97: JMP $9D9E ; goto holdButtons;
moveInProgress:
9D9A: LDA #$00
9D9C: STA $00F5 ; clearNewlyPressedButtons();
holdButtons:
9D9E: LDA $00CE
9DA0: STA $00F7 ; setHeldButtons(heldButtons);
9DA2: RTS ; return;
startButtonPressed:
9DA3: LDA #$DD
9DA5: STA $00D2 ; reset index;
9DA7: LDA #$00
9DA9: STA $00B2 ; counter = 0;
9DAB: LDA #$01
9DAD: STA $00C0 ; gameMode = TITLE_SCREEN;
9DAF: RTS ; return;$00D1$00D2$872D9DE8: LDA $00D1
9DEA: CLC ; increment [$00D1]
9DEB: ADC #$01 ; possibly causing wrap around to 0
9DED: STA $00D1 ; which produces a carry
9DEF: LDA #$00
9DF1: ADC $00D2
9DF3: STA $00D2 ; add carry to [$00D2]
9DF5: RTS ; return$00D0$FF. At the same time, the following code is launched, intended for writing to the table of demo buttons.
However, the table is stored in the PRG-ROM. Attempting to write to it will not affect the stored data. Instead, each write operation triggers a bank switch, which leads to the glitch effect shown below.recording:
9DB0: JSR $AB9D ; pollController();
9DB3: LDA $00C0 ; if (gameMode != DEMO) {
9DB5: CMP #$05 ; return;
9DB7: BNE $9DE7 ; }
9DB9: LDA $00D0 ; if (not recording mode) {
9DBB: CMP #$FF ; return;
9DBD: BNE $9DE7 ; }
9DBF: LDA $00F7 ; if (getHeldButtons() == heldButtons) {
9DC1: CMP $00CE ; goto buttonsNotChanged;
9DC3: BEQ $9DE4 ; }
9DC5: LDX #$00
9DC7: LDA $00CE
9DC9: STA ($D1,X) ; demoButtonsTable[index] = heldButtons;
9DCB: JSR $9DE8 ; index++;
9DCE: LDA $00CF
9DD0: STA ($D1,X) ; demoButtonsTable[index] = repeats;
9DD2: JSR $9DE8 ; index++;
9DD5: LDA $00D2 ; if (reached end of demo table) {
9DD7: CMP #$DF ; return;
9DD9: BEQ $9DE7 ; }
9DDB: LDA $00F7
9DDD: STA $00CE ; heldButtons = getHeldButtons();
9DDF: LDA #$00
9DE1: STA $00CF ; repeats = 0;
9DE3: RTS ; return;
buttonsNotChanged:
9DE4: INC $00CF ; repeats++;
9DE6: RTS
9DE7: RTS ; return;
This suggests that developers could run the program partially or completely in RAM.
To get around this obstacle, I created
lua/RecordDemo.lua, located in the zip source . After switching to the demo recording mode, it redirects the write operations to the table to the Lua console. From it, the bytes can be copied and pasted into the ROM.To record your own demo, run FCEUX and download the Nintendo Tetris ROM file (File | Open ROM ...). Then open the Lua Script window (File | Lua | New Lua Script Window ...), go to the file or enter the path. Click the Run button to start the demo recording mode, and then click the FCEUX window to switch focus to it. You can control the shapes until the table of buttons is filled. After that, the game will automatically return to the splash screen. Click Stop in the Lua Script window to stop the script. Recorded data will appear in the Output Console, as shown in the figure below.

Select all content and copy to clipboard (Ctrl + C). Then run the Hex Editor (Debug | Hex Editor ...). From the Hex Editor menu, select View | ROM File, and then File | Goto Address. In the Goto dialog box, enter 5D10 (the address of the table of demo buttons in the ROM file) and click Ok. Then paste the contents of the clipboard (Ctrl + V).

Finally in the FCEUX menu, select NES | Reset If you managed to repeat all these steps, then the demo should be replaced with your own version.
If you want to save the changes, in the Hex Editor menu, select File | Save Rom As ... and enter the name of the modified ROM file, and then click Save.
Similarly, you can customize the sequence created by Tetrimino.
Death screen
As mentioned above, the majority of players cannot cope with the speed of descent of figures at level 29, which quickly leads to the completion of the game. Therefore, the players he became associated with the name "screen of death." But from a technical point of view, the death screen does not allow the player to go further because of the bug, in which the quick descent actually turns out to be not a bug, but features. The designers were so kind that they allowed the game to continue as long as the player was able to withstand superhuman speed.
This screen of death occurs on about 1,550 rows removed. It manifests itself in different ways. Sometimes the game reloads. In other cases, the screen just turns black. Usually, the game freezes (“freezes”) immediately after deleting a row, as shown below. Such effects are often preceded by random graphic artifacts.

The screen of death is the result of a bug in the code that adds points when deleting rows. The six-character account is stored as a 24-bit packed BCD little endian and is located at
$0053- $0055. A table is used to convert between the number of rows cleared and points received; each entry in it is a 16-bit BCD value little endian.
After incrementing the total number of rows, and possibly the level, the value in this list is multiplied by the level number plus one, and the result is added to the points. This is amply demonstrated in the table from the Nintendo Tetris guide booklet:9CA5: 00 00 ; 0: 0
9CA7: 40 00 ; 1: 40
9CA9: 00 01 ; 2: 100
9CAB: 00 03 ; 3: 300
9CAD: 00 12 ; 4: 1200
As shown below, the multiplication is simulated by a cycle that adds points to the score. It is executed after blocking the shape, even if no rows are cleared. Unfortunately, the Ricoh 2A03 does not have the 6502 processor binary-decimal mode; he could greatly simplify the body of the cycle. Instead, the addition is done in steps, using the binary mode. Any digit that exceeds the value of 9 after the addition is essentially obtained by subtracting 10 and the increment of the digit on the left. For example, that is converted to . But this scheme is not fully protected. Take : verification is not able to convert the result to
9C31: LDA $0044
9C33: STA $00A8
9C35: INC $00A8 ; for(i = 0; i <= level; i++) {
9C37: LDA $0056
9C39: ASL
9C3A: TAX
9C3B: LDA $9CA5,X ; points[0] = pointsTable[2 * completedLines];
9C3E: CLC
9C3F: ADC $0053
9C41: STA $0053 ; score[0] += points[0];
9C43: CMP #$A0
9C45: BCC $9C4E ; if (upper digit of score[0] > 9) {
9C47: CLC
9C48: ADC #$60
9C4A: STA $0053 ; upper digit of score[0] -= 10;
9C4C: INC $0054 ; score[1]++;
; }
9C4E: INX
9C4F: LDA $9CA5,X ; points[1] = pointsTable[2 * completedLines + 1];
9C52: CLC
9C53: ADC $0054
9C55: STA $0054 ; score[1] += points[1];
9C57: AND #$0F
9C59: CMP #$0A
9C5B: BCC $9C64 ; if (lower digit of score[1] > 9) {
9C5D: LDA $0054
9C5F: CLC ; lower digit of score[1] -= 10;
9C60: ADC #$06 ; increment upper digit of score[1];
9C62: STA $0054 ; }
9C64: LDA $0054
9C66: AND #$F0
9C68: CMP #$A0
9C6A: BCC $9C75 ; if (upper digit of score[1] > 9) {
9C6C: LDA $0054
9C6E: CLC
9C6F: ADC #$60
9C71: STA $0054 ; upper digit of score[1] -= 10;
9C73: INC $0055 ; score[2]++;
; }
9C75: LDA $0055
9C77: AND #$0F
9C79: CMP #$0A
9C7B: BCC $9C84 ; if (lower digit of score[2] > 9) {
9C7D: LDA $0055
9C7F: CLC ; lower digit of score[2] -= 10;
9C80: ADC #$06 ; increment upper digit of score[2];
9C82: STA $0055 ; }
9C84: LDA $0055
9C86: AND #$F0
9C88: CMP #$A0
9C8A: BCC $9C94 ; if (upper digit of score[2] > 9) {
9C8C: LDA #$99
9C8E: STA $0053
9C90: STA $0054
9C92: STA $0055 ; max out score to 999999;
; }
9C94: DEC $00A8
9C96: BNE $9C37 ; }$07 + $07 = $0E$14$09 + $09 = $12$18. To compensate for this, none of the decimal digits in the scores table entries exceeds 6. In addition, the test can be used, the last digit of all entries is always 0. It takes time to complete this long and complex cycle. At large levels, a large number of iterations affect the timing of the game, because the generation of each frame takes more than 1/60 of a second. All this as a result leads to different manifestations of the “death screen”.
The AI script on Lua limits the number of iterations in the loop to 30 — the maximum value that the designers intended could be reached by the players, which makes it possible to eliminate the screen of death.
Endings
In the Nintendo Tetris guide booklet, an A-Type game is described as:

The game rewards players who score large enough points in one of the five animations of the endings. The choice of ending is entirely based on the two leftmost digits of the six-digit count. As shown below, to get one of the endings, the player must score at least 30,000 points. It is worth noting that - - this is a mirror of addresses - . The account is duplicated by addresses - . After passing the first test, the animation of the ending is selected with the following switch statement.
9A4D: LDA $0075
9A4F: CMP #$03
9A51: BCC $9A5E ; if (score[2] >= $03) {
9A53: LDA #$80
9A55: JSR $A459
9A58: JSR $9E3A
9A5B: JMP $9A64 ; select ending;
; }$0060$007F$0040$005F$0073$0075A96E: LDA #$00
A970: STA $00C4
A972: LDA $0075 ; if (score[2] < $05) {
A974: CMP #$05 ; ending = 0;
A976: BCC $A9A5 ; }
A978: LDA #$01
A97A: STA $00C4
A97C: LDA $0075 ; else if (score[2] < $07) {
A97E: CMP #$07 ; ending = 1;
A980: BCC $A9A5 ; }
A982: LDA #$02
A984: STA $00C4
A986: LDA $0075 ; else if (score[2] < $10) {
A988: CMP #$10 ; ending = 2;
A98A: BCC $A9A5 ; }
A98C: LDA #$03
A98E: STA $00C4
A990: LDA $0075 ; else if (score[2] < $12) {
A992: CMP #$12 ; ending = 3;
A994: BCC $A9A5 ; }
A996: LDA #$04 ; else {
A998: STA $00C4 ; ending = 4;
; }At the end of the rocket of increasing size are launched from the launch pad next to St. Basil's Cathedral. In the fourth ending, the Buran spacecraft is shown - the Soviet version of the American Space Shuttle. In the best ending, the cathedral itself rises in the air, and a UFO hangs above the launch pad. Below is a picture of each ending and the score associated with it.
30000–49999 | 50000–69999 | 70000–99999 |
100000–119999 | 120000+ |
In the B-Type game mode, another test is implemented, which is described in the Nintendo Tetris guide booklet as follows:

If the player successfully clears 25 rows, the game shows the ending, depending on the initial level. The endings for levels 0–8 consist of animals and objects flying or running in the frame, mysteriously passing behind St. Basil's Cathedral. A UFO from the best ending of the A-Type mode appears in the ending 3. In the ending 4, extinct flying pterosaurs appear, and in the ending 7 mythical flying dragons are shown. In the endings 2 and 6, wingless birds are shown: running penguins and ostriches. In the end 5, the sky is filled with GOOD airships (not to be confused with Goodyear airships). And in the end 8, a lot of “Burans” rush through the screen, although in reality it was only one.
The initial height (plus 1) is used as a multiplier, rewarding the player with a large number of animals / objects for increased complexity.
In the best B-Type ending, the castle is filled with characters from the Nintendo universe: Princess Peach claps her hands, Kid Icarus plays the violin, Donki Kong knocks on the big drum, Mario and Luigi dance, Bowser plays the accordion, Samus plays the cello, Link - on the flute, while the domes of St. Basil’s Cathedral soar into the air. From the initial height depends on the number of these elements shown in the end. Below are the images of all 10 endings.
 |  |  |
 |  |  |
 |  |  |
 |
The AI can quickly clear all 25 rows required in the B-Type mode at any initial level and height, allowing you to view any of the endings. It is also worth assessing how cool he is with large piles of random blocks.
In the endings 0–8, up to 6 objects can move in the frame. The y coordinates of the objects are stored in a table located at
$A7B7.
Horizontal distances between objects are stored in a table at .
The sequence of values with a sign at the address determines the speed and direction of objects.
Sprite indices are stored at .
In fact, each object consists of two sprites with adjacent indexes. For the second index you need to add 1. For example, a dragon consists ofA7B7: 98 A8 C0 A8 90 B0 ; 0
A7BD: B0 B8 A0 B8 A8 A0 ; 1
A7C3: C8 C8 C8 C8 C8 C8 ; 2
A7C9: 30 20 40 28 A0 80 ; 3
A7CF: A8 88 68 A8 48 78 ; 4
A7D5: 58 68 18 48 78 38 ; 5
A7DB: C8 C8 C8 C8 C8 C8 ; 6
A7E1: 90 58 70 A8 40 38 ; 7
A7E7: 68 88 78 18 48 A8 ; 8$A77BA77B: 3A 24 0A 4A 3A FF ; 0
A781: 22 44 12 32 4A FF ; 1
A787: AE 6E 8E 6E 1E 02 ; 2
A78D: 42 42 42 42 42 02 ; 3
A793: 22 0A 1A 04 0A FF ; 4
A799: EE DE FC FC F6 02 ; 5
A79F: 80 80 80 80 80 FF ; 6
A7A5: E8 E8 E8 E8 48 FF ; 7
A7AB: 80 AE 9E 90 80 02 ; 8$A771A771: 01 ; 0: 1
A772: 01 ; 1: 1
A773: FF ; 2: -1
A774: FC ; 3: -4
A775: 01 ; 4: 1
A776: FF ; 5: -1
A777: 02 ; 6: 2
A778: 02 ; 7: 2
A779: FE ; 8: -1$A7F3A7F3: 2C ; 0: dragonfly
A7F4: 2E ; 1: dove
A7F5: 54 ; 2: penguin
A7F6: 32 ; 3: UFO
A7F7: 34 ; 4: pterosaur
A7F8: 36 ; 5: blimp
A7F9: 4B ; 6: ostrich
A7FA: 38 ; 7: dragon
A7FB: 3A ; 8: Buran$38and $39. The tiles for these sprites are contained in the pattern tables shown below. |  |  |
The central table of the pattern we considered above, it is used to display tetrimino and the playing field. Interestingly, it contains the entire alphabet, while others contain only part of it to save space. But even more interesting are the sprites of the aircraft and the helicopter in the pattern table on the left; they do not appear in the endings or in other parts of the game. It turned out that the plane and the helicopter have indexes sprites
$30and $16and you can change the table shown above, to see them in action.

Unfortunately, the helicopter supports are not displayed, but the main and tail rotors are beautifully animated.
2 Player Versus
Nintendo Tetris contains an unfinished two-player mode, which can be turned on by changing the number of players (
$00BE) by 2. As shown below, two game fields appear in the background of the single-player mode.
There is no border between the fields, because the central background area has a solid black color. The values
003shown above the playing fields indicate the number of rows cleared by each player. The only figure common for two players appears in the same place as in single player mode. Unfortunately, it is on the right playing field. Squares and other tiles are incorrectly painted. And when a player loses the game is restarted. But if you do not take into account these problems, the mode is quite playable. Each player can independently control the pieces in the corresponding playing field. And when a player enters Double, Triple or Tetris (that is, clears two, three or four rows), trash cans appear at the bottom of the playing field with one missing square.
An additional field is located at
$0500. A $0060- $007Fusually being a mirror $0040- $005F, is used for the second player. Probably, this interesting mode was abandoned due to the tight development schedule. And perhaps he was left unfinished on purpose. One of the reasons Tetris was selected as the game that came with the Nintendo Game Boy was that it encouraged him to buy Game Link Cable- an accessory that connected together two Game Boy to launch 2 player versus mode. This cable added an element of "sociality" to the system - pushing friends to buy a Game Boy to join in the fun. Perhaps Nintendo feared that if in the console version of the game there would be 2 player versus mode, then the Tetris advertising power, which stimulated the purchase of a Game Boy, could be weakened.
Music and sound effects
Background music is turned on when
$06F5one of the values listed in the table is assigned.| Value | Description |
|---|---|
01 | Unused splash screen music |
02 | B-Type Mode Target Achieved |
03 | Music-1 |
04 | Music-2 |
05 | Music-3 |
06 | Music-1 allegro |
07 | Music-2 allegro |
08 | Music-3 allegro |
09 | Congratulations screen |
0A | Endings |
0B | B-Type Mode Target Achieved |
Music-1 is a version of Dance of the Fairy Drazhe , music for the ballerina from Tchaikovsky 's Nutcracker, the third act of the pas de Vallors . The ending music is a variation of The Bullfighter's Couplets , arias from the opera by Carmen Georges Bizet. These compositions are arranged by the composer for the rest of the music of the game Hirokazu Tanaka . Music-2 was inspired by traditional Russian folk songs. Music-3 is mysterious, futuristic and tender; for a while, it was the melody of a Nintendo of America customer support phone call.
To help the player get into a state of panic, when the height of the heap approaches the ceiling of the playing field, a fast paced version of the background music (
$06- $08) begins to play . Interestingly, among the musical compositions there is no " Korobeinikov ", a famous theme, sounding in Game Boy Tetris.
Sound effects are triggered by recording to
$06F0and $06F1, according to the following table.| Address | Value | Description |
|---|---|---|
06F0 | 02 | Curtain end game |
06F0 | 03 | Rocket in the end |
06F1 | 01 | Select menu option |
06F1 | 02 | Menu screen selection |
06F1 | 03 | Tetrimino shift |
06F1 | 04 | Tetris received |
06F1 | 05 | Tetrimino turn |
06F1 | 06 | New level |
06F1 | 07 | Tetrimino lock |
06F1 | 08 | Chirping |
06F1 | 09 | Row cleaning |
06F1 | 0A | The row is full |
Game states and rendering modes
During gameplay, the current state of the game is represented by an integer number at
$0048. Most of the time it matters $01, meaning that the player controls the active Tetrimino. However, when the figure is blocked in place, the game gradually passes from state $02to state $08, as shown in the table.| condition | Description |
|---|---|
00 | Unassigned orientation ID |
01 | Player controls active tetrimino |
02 | Tetrimino lock on the playing field |
03 | Verification of filled lines |
04 | Displaying row cleaning animation |
05 | Update rows and statistics |
06 | Check B-Type Mode Target |
07 | Not used |
08 | Create the following tetrimino |
09 | Not used |
0A | Update curtain end game |
0B | Game state increment |
Code branching, depending on the game state, occurs at the address
$81B2:
In the switch state , jumps to the code assigning a value indicating that the orientation is not set.
The handler is never called; however, the game state serves as a signal for other parts of the code.
The state allows the player to shift, rotate, and lower the active Tetrimino:
As stated in the previous sections, the subroutines for shifting, rotating, and lowering the figure check for new Tetrimino positions before executing the code. The only way to block a shape in the wrong position is to create it on top of an existing shape. In this game ends. As shown below, this check is performed by the status code.81B2: LDA $0048
81B4: JSR $AC82 ; switch(playState) {
81B7: 2F 9E ; case 00: goto 9E2F; // Unassign orientationID
81B9: CF 81 ; case 01: goto 81CF; // Player controls active Tetrimino
81BB: A2 99 ; case 02: goto 99A2; // Lock Tetrimino into playfield
81BD: 6B 9A ; case 03: goto 9A6B; // Check for completed rows
81BF: 39 9E ; case 04: goto 9E39; // Display line clearing animation
81C1: 58 9B ; case 05: goto 9B58; // Update lines and statistics
81C3: F2 A3 ; case 06: goto A3F2; // B-Type goal check; Unused frame for A-Type
81C5: 03 9B ; case 07: goto 9B03; // Unused frame; Execute unfinished 2 player mode logic
81C7: 8E 98 ; case 08: goto 988E; // Spawn next Tetrimino
81C9: 39 9E ; case 09: goto 9E39; // Unused
81CB: 11 9A ; case 0A: goto 9A11; // Update game over curtain
81CD: 37 9E ; case 0B: goto 9E37; // Increment play state
; }$00orientationID$139E2F: LDA #$13
9E31: STA $0042 ; orientationID = UNASSIGNED;
9E33: RTS ; return;$00$0181CF: JSR $89AE ; shift Tetrimino;
81D2: JSR $88AB ; rotate Tetrimino;
81D5: JSR $8914 ; drop Tetrimino;
81D8: RTS ; return;$02.
If the locked position is correct, it marks the 4 associated game field cells as occupied. Otherwise, it makes the transition to the state - the ominous curtain of the end of the game.99A2: JSR $948B ; if (new position valid) {
99A5: BEQ $99B8 ; goto updatePlayfield;
; }
99A7: LDA #$02
99A9: STA $06F0 ; play curtain sound effect;
99AC: LDA #$0A
99AE: STA $0048 ; playState = UPDATE_GAME_OVER_CURTAIN;
99B0: LDA #$F0
99B2: STA $0058 ; curtainRow = -16;
99B4: JSR $E003 ; updateAudio();
99B7: RTS ; return;$0A
The curtain is drawn down from the top of the playing field, going down one line every 4 frames.
curtainRow( $0058) is initialized with a value of −16, creating an additional delay of 0.27 seconds between the final lock and the start of the animation. The address $9A21in the $0Acode shown below is used to access the multiplication table, which is erroneously displayed as level numbers. This is done to scale curtainRowto 10. In addition, as shown above, the code at the address $9A51starts the animation of the ending, if the player’s account is at least 30,000 points; otherwise, it waits to press Start.
The code is completed by assigning a value to the game state , but the corresponding handler is not called because the game is over.9A11: LDA $0058 ; if (curtainRow == 20) {
9A13: CMP #$14 ; goto endGame;
9A15: BEQ $9A47 ; }
9A17: LDA $00B1 ; if (frameCounter not divisible by 4) {
9A19: AND #$03 ; return;
9A1B: BNE $9A46 ; }
9A1D: LDX $0058 ; if (curtainRow < 0) {
9A1F: BMI $9A3E ; goto incrementCurtainRow;
; }
9A21: LDA $96D6,X
9A24: TAY ; rowIndex = 10 * curtainRow;
9A25: LDA #$00
9A27: STA $00AA ; i = 0;
9A29: LDA #$13
9A2B: STA $0042 ; orientationID = NONE;
drawCurtainRow:
9A2D: LDA #$4F
9A2F: STA ($B8),Y ; playfield[rowIndex + i] = CURTAIN_TILE;
9A31: INY
9A32: INC $00AA ; i++;
9A34: LDA $00AA
9A36: CMP #$0A ; if (i != 10) {
9A38: BNE $9A2D ; goto drawCurtainRow;
; }
9A3A: LDA $0058
9A3C: STA $0049 ; vramRow = curtainRow;
incrementCurtainRow:
9A3E: INC $0058 ; curtainRow++;
9A40: LDA $0058 ; if (curtainRow != 20) {
9A42: CMP #$14 ; return;
9A44: BNE $9A46 ; }
9A46: RTS ; return;
endGame:
9A47: LDA $00BE
9A49: CMP #$02
9A4B: BEQ $9A64 ; if (numberOfPlayers == 1) {
9A4D: LDA $0075
9A4F: CMP #$03
9A51: BCC $9A5E ; if (score[2] >= $03) {
9A53: LDA #$80
9A55: JSR $A459
9A58: JSR $9E3A
9A5B: JMP $9A64 ; select ending;
; }
9A5E: LDA $00F5 ; if (not just pressed Start) {
9A60: CMP #$10 ; return;
9A62: BNE $9A6A ; }
; }
9A64: LDA #$00
9A66: STA $0048 ; playState = INITIALIZE_ORIENTATION_ID;
9A68: STA $00F5 ; clear newly pressed buttons;
9A6A: RTS ; return;$00The lines of the playing field are incrementally copied to VRAM for display. The index of the current copied string is contained in
vramRow( $0049). The address is $9A3CvramRowassigned a value curtainRow, which ultimately makes this line visible when rendering. Manipulations with VRAM occur during the vertical blanking interval, which is recognized by the interrupt handler described in the “Legal Information Screen” section. It calls the subroutine shown below (marked in the comments of the interrupt handler as
render()).
The rendering mode is similar to the game mode. It is stored at an address and can be one of the following values:804B: LDA $00BD
804D: JSR $AC82 ; switch(renderMode) {
8050: B1 82 ; case 0: goto 82B1; // Legal and title screens
8052: DA 85 ; case 1: goto 85DA; // Menu screens
8054: 44 A3 ; case 2: goto A344; // Congratulations screen
8056: EE 94 ; case 3: goto 94EE; // Play and demo
8058: 95 9F ; case 4: goto 9F95; // Ending animation
; }$00BD| Value | Description |
|---|---|
00 | Screen with jur. information and screen saver |
01 | Menu screens |
02 | Congratulations screen |
03 | Game and demo |
04 | An animation of the ending |
Part of the rendering mode is
$03shown below.
As you can see below, it sends to VRAM the string of the playing field that has an index . If more than 20, the subroutine does nothing.
The table ( ) contains VRAM addresses in little endian format corresponding to the displayed lines of the playing field shifted by 6 in normal mode and −2 and 12 for the playing field in unfinished 2 Player Versus mode. The bytes of this table are part of a list of values that are erroneously displayed as level numbers after level 29. The adjacent lower and upper bytes of each address are obtained separately and are essentially combined into a 16-bit address that is used in the copy cycle.
At the end of the subroutine, the increment is executed.952A: JSR $9725 ; copyPlayfieldRowToVRAM();
952D: JSR $9725 ; copyPlayfieldRowToVRAM();
9530: JSR $9725 ; copyPlayfieldRowToVRAM();
9533: JSR $9725 ; copyPlayfieldRowToVRAM();copyPlayfieldRowToVRAM()vramRowvramRow9725: LDX $0049 ; if (vramRow > 20) {
9727: CPX #$15 ; return;
9729: BPL $977E ; }
972B: LDA $96D6,X
972E: TAY ; playfieldAddress = 10 * vramRow;
972F: TXA
9730: ASL
9731: TAX
9732: INX ; high = vramPlayfieldRows[vramRow * 2 + 1];
9733: LDA $96EA,X
9736: STA $2006
9739: DEX
973A: LDA $00BE
973C: CMP #$01
973E: BEQ $975E ; if (numberOfPlayers == 2) {
9740: LDA $00B9
9742: CMP #$05
9744: BEQ $9752 ; if (leftPlayfield) {
9746: LDA $96EA,X
9749: SEC
974A: SBC #$02
974C: STA $2006 ; low = vramPlayfieldRows[vramRow * 2] - 2;
974F: JMP $9767 ; } else {
9752: LDA $96EA,X
9755: CLC
9756: ADC #$0C
9758: STA $2006 ; low = vramPlayfieldRows[vramRow * 2] + 12;
975B: JMP $9767 ; } else {
975E: LDA $96EA,X
9761: CLC
9762: ADC #$06 ; low = vramPlayfieldRows[vramRow * 2] + 6;
9764: STA $2006 ; }
; vramAddress = (high << 8) | low;
9767: LDX #$0A
9769: LDA ($B8),Y
976B: STA $2007
976E: INY ; for(i = 0; i < 10; i++) {
976F: DEX ; vram[vramAddress + i] = playfield[playfieldAddress + i];
9770: BNE $9769 ; }
9772: INC $0049 ; vramRow++;
9774: LDA $0049 ; if (vramRow < 20) {
9776: CMP #$14 ; return;
9778: BMI $977E ; }
977A: LDA #$20
977C: STA $0049 ; vramRow = 32;
977E: RTS ; return;vramPlayfieldRows$96EAvramRow. If the value reaches 20, then it is assigned a value of 32, meaning that the copying is fully completed. As shown above, only 4 lines are copied per frame. The state handler
$03is responsible for recognizing completed lines and removing them from the playing field. For 4 separate calls, it scans the offsets of the lines [−2, 1]near the center of tetrimino (both coordinates of all the squares of tetrimino are in this interval). Indexes of completed lines are stored at $004A- $004D; The recorded index 0 is used to indicate that no complete line was found in this passage. The handler is shown below.
Verification at the beginning does not allow the handler to perform when transferring the lines of the playing field to VRAM (state handler9A6B: LDA $0049
9A6D: CMP #$20 ; if (vramRow < 32) {
9A6F: BPL $9A74 ; return;
9A71: JMP $9B02 ; }
9A74: LDA $0041 ; rowY = tetriminoY - 2;
9A76: SEC
9A77: SBC #$02 ; if (rowY < 0) {
9A79: BPL $9A7D ; rowY = 0;
9A7B: LDA #$00 ; }
9A7D: CLC
9A7E: ADC $0057
9A80: STA $00A9 ; rowY += lineIndex;
9A82: ASL
9A83: STA $00A8
9A85: ASL
9A86: ASL
9A87: CLC
9A88: ADC $00A8
9A8A: STA $00A8 ; rowIndex = 10 * rowY;
9A8C: TAY
9A8D: LDX #$0A
9A8F: LDA ($B8),Y
9A91: CMP #$EF ; for(i = 0; i < 10; i++) {
9A93: BEQ $9ACC ; if (playfield[rowIndex + i] == EMPTY_TILE) {
9A95: INY ; goto rowNotComplete;
9A96: DEX ; }
9A97: BNE $9A8F ; }
9A99: LDA #$0A
9A9B: STA $06F1 ; play row completed sound effect;
9A9E: INC $0056 ; completedLines++;
9AA0: LDX $0057
9AA2: LDA $00A9
9AA4: STA $4A,X ; lines[lineIndex] = rowY;
9AA6: LDY $00A8
9AA8: DEY
9AA9: LDA ($B8),Y
9AAB: LDX #$0A
9AAD: STX $00B8
9AAF: STA ($B8),Y
9AB1: LDA #$00
9AB3: STA $00B8
9AB5: DEY ; for(i = rowIndex - 1; i >= 0; i--) {
9AB6: CPY #$FF ; playfield[i + 10] = playfield[i];
9AB8: BNE $9AA9 ; }
9ABA: LDA #$EF
9ABC: LDY #$00
9ABE: STA ($B8),Y
9AC0: INY ; for(i = 0; i < 10; i++) {
9AC1: CPY #$0A ; playfield[i] = EMPTY_TILE;
9AC3: BNE $9ABE ; }
9AC5: LDA #$13
9AC7: STA $0042 ; orientationID = UNASSIGNED;
9AC9: JMP $9AD2 ; goto incrementLineIndex;
rowNotComplete:
9ACC: LDX $0057
9ACE: LDA #$00
9AD0: STA $4A,X ; lines[lineIndex] = 0;
incrementLineIndex:
9AD2: INC $0057 ; lineIndex++;
9AD4: LDA $0057 ; if (lineIndex < 4) {
9AD6: CMP #$04 ; return;
9AD8: BMI $9B02 ; }
9ADA: LDY $0056
9ADC: LDA $9B53,Y
9ADF: CLC
9AE0: ADC $00BC
9AE2: STA $00BC ; totalGarbage += garbageLines[completedLines];
9AE4: LDA #$00
9AE6: STA $0049 ; vramRow = 0;
9AE8: STA $0052 ; clearColumnIndex = 0;
9AEA: LDA $0056
9AEC: CMP #$04
9AEE: BNE $9AF5 ; if (completedLines == 4) {
9AF0: LDA #$04 ; play Tetris sound effect;
9AF2: STA $06F1 ; }
9AF5: INC $0048 ; if (completedLines > 0) {
9AF7: LDA $0056 ; playState = DISPLAY_LINE_CLEARING_ANIMATION;
9AF9: BNE $9B02 ; return;
; }
9AFB: INC $0048 ; playState = UPDATE_LINES_AND_STATISTICS;
9AFD: LDA #$07
9AFF: STA $06F1 ; play piece locked sound effect;
9B02: RTS ; return;vramRow$03called in each frame). If the filled rows are found, it is vramRowreset to 0, which causes the full transfer to be performed. lineIndex( $00A9) is initialized with a value of 0 and its increment is executed in each pass. Unlike the game state
$0Aand subroutines to copy the playing field, which use the multiplication table at an address $96D6, a block that starts with $9A82multiplies rowYby 10 using shifts and addition: rowIndex = (rowY << 1) + (rowY << 3); // rowIndex = 2 * rowY + 8 * rowY;This is done only because it is
rowYlimited by an interval [0, 20], and the multiplication table covers only [0, 19]. Scanning rows can go beyond the end of the playing field. However, as said earlier, the game initializes $0400- $04FFwith the value$EF(empty tile), creating more than 5 additional empty hidden lines under the floor of the playing field. The block starting with
$9ADAis part of the unfinished 2 Player Versus mode. As stated above, cleaning up the ranks adds trash to the opponent’s playing field. The number of garbage rows is determined by the table at $9B53:
The cycle at the address shifts the material above the filled row one line down. It takes advantage of the fact that each line in continuous sequence is separated from the other by 10 bytes. The next loop clears the top row.
The row cleaning animation is performed during the game state , but as shown below, it does not occur in the game state handler, which is completely empty.
Instead, during the game state9B53: 00 ; no cleared lines
9B54: 00 ; Single
9B55: 01 ; Double
9B56: 02 ; Triple
9B57: 04 ; Tetris$9AA6$049E39: RTS ; return;$04The following branching rendering mode is performed $03. and mirrored values are needed for unfinished 2 Player Versus mode.
The subroutine is shown below . It is called in each frame, but the condition at the beginning allows it to be performed only in every fourth frame. In each pass, it cycles through the list of indexes of completed rows and clears 2 columns in these rows, moving from the center column to the outside.
The 16-bit VRAM address is composed in the same way that is shown in the playing field copying routine. However, in this case, it performs an offset to the column index obtained from the table shown below.
Cleaning animation requires 5 passes. Then the code goes to the next game state.
Game state handler94EE: LDA $0068
94F0: CMP #$04
94F2: BNE $9522 ; if (playState == DISPLAY_LINE_CLEARING_ANIMATION) {
94F4: LDA #$04
94F6: STA $00B9 ; leftPlayfield = true;
94F8: LDA $0072
94FA: STA $0052
94FC: LDA $006A
94FE: STA $004A
9500: LDA $006B
9502: STA $004B
9504: LDA $006C
9506: STA $004C
9508: LDA $006D
950A: STA $004D
950C: LDA $0068
950E: STA $0048 ; mirror values;
9510: JSR $977F ; updateLineClearingAnimation();
; ...
; }leftPlayfieldupdateLineClearingAnimation()977F: LDA $00B1 ; if (frameCounter not divisible by 4) {
9781: AND #$03 ; return;
9783: BNE $97FD ; }
9785: LDA #$00 ; for(i = 0; i < 4; i++) {
9787: STA $00AA ; rowY = lines[i];
9789: LDX $00AA ; if (rowY == 0) {
978B: LDA $4A,X ; continue;
978D: BEQ $97EB ; }
978F: ASL
9790: TAY
9791: LDA $96EA,Y
9794: STA $00A8 ; low = vramPlayfieldRows[2 * rowY];
9796: LDA $00BE ; if (numberOfPlayers == 2) {
9798: CMP #$01 ; goto twoPlayers;
979A: BNE $97A6 ; }
979C: LDA $00A8
979E: CLC
979F: ADC #$06
97A1: STA $00A8 ; low += 6;
97A3: JMP $97BD ; goto updateVRAM;
twoPlayers:
97A6: LDA $00B9
97A8: CMP #$04
97AA: BNE $97B6 ; if (leftPlayfield) {
97AC: LDA $00A8
97AE: SEC
97AF: SBC #$02
97B1: STA $00A8 ; low -= 2;
97B3: JMP $97BD ; } else {
97B6: LDA $00A8
97B8: CLC
97B9: ADC #$0C ; low += 12;
97BB: STA $00A8 ; }
updateVRAM:
97BD: INY
97BE: LDA $96EA,Y
97C1: STA $00A9
97C3: STA $2006
97C6: LDX $0052 ; high = vramPlayfieldRows[2 * rowY + 1];
97C8: LDA $97FE,X
97CB: CLC ; rowAddress = (high << 8) | low;
97CC: ADC $00A8
97CE: STA $2006 ; vramAddress = rowAddress + leftColumns[clearColumnIndex];
97D1: LDA #$FF
97D3: STA $2007 ; vram[vramAddress] = 255;
97D6: LDA $00A9
97D8: STA $2006
97DB: LDX $0052 ; high = vramPlayfieldRows[2 * rowY + 1];
97DD: LDA $9803,X
97E0: CLC ; rowAddress = (high << 8) | low;
97E1: ADC $00A8
97E3: STA $2006 ; vramAddress = rowAddress + rightColumns[clearColumnIndex];
97E6: LDA #$FF
97E8: STA $2007 ; vram[vramAddress] = 255;
97EB: INC $00AA
97ED: LDA $00AA
97EF: CMP #$04
97F1: BNE $9789 ; }
97F3: INC $0052 ; clearColumnIndex++;
97F5: LDA $0052 ; if (clearColumnIndex < 5) {
97F7: CMP #$05 ; return;
97F9: BMI $97FD ; }
97FB: INC $0048 ; playState = UPDATE_LINES_AND_STATISTICS;
97FD: RTS ; return;97FE: 04 03 02 01 00 ; left columns
9803: 05 06 07 08 09 ; right columns$05contains the code described in the “Series and Statistics” section. The handler ends with this code: The
variable is not reset until the completion of the game state , after which it is used to update the total number of rows and the score. This sequence allows for an interesting bug. In the demo mode, you need to wait until the game has collected a full row, and then quickly press Start, until the row cleaning animation has ended. The game will return to the splash screen, but if you select the correct time, the value will remain. Now you can start the game in A-Type mode. When locking in place of the first figure, the game state handler will begin scanning the completed rows. He will not find them, but will leave them unchanged. Finally, when executing the game state9C9E: LDA #$00
9CA0: STA $0056 ; completedLines = 0;
9CA2: INC $0048 ; playState = B_TYPE_GOAL_CHECK;
9CA4: RTS ; return;completedLines$05completedLines$03completedLines$05the total number of rows and the score will increase, as if you had typed them. The easiest way to do this and get the most, waiting for the demo to collect Tetris (there will be 2 in the demo). As soon as you see the screen flicker, press Start.

After starting a new game, the screen will continue to flicker. All this thanks to the following code, called the interrupt handler. In fact, if you let the first piece automatically descend to the floor of the playing field, the score will increase by an even greater value, because ( ) also saves its value from the demo. This is true even in cases where the demo did not fill a single row. is not reset until the Down button is pressed. Moreover, if you press Start during the animation of cleaning the rows of the Tetris combination in demo mode, and then wait for the demo to start again, the demo will not only score points for Tetris, but will also confuse the entire timing. As a result, the demo will lose the game. After the end of the game curtain, you can return to the splash screen by clicking on Start.
9673: LDA #$3F
9675: STA $2006
9678: LDA #$0E
967A: STA $2006 ; prepare to modify background tile color;
967D: LDX #$00 ; color = DARK_GRAY;
967F: LDA $0056
9681: CMP #$04
9683: BNE $9698 ; if (completedLines == 4) {
9685: LDA $00B1
9687: AND #$03
9689: BNE $9698 ; if (frameCounter divisible by 4) {
968B: LDX #$30 ; color = WHITE;
968D: LDA $00B1
968F: AND #$07
9691: BNE $9698 ; if (frameCounter divisible by 8) {
9693: LDA #$09
9695: STA $06F1 ; play clear sound effect;
; }
; }
; }
9698: STX $2007 ; update background tile color;holdDownPoints$004FholdDownPointsThe game state
$06performs a goal check for B-Type mode games. In A-Type mode, it is essentially an unused frame. The game state
$07contains only the unfinished mode logic 2 Player Versus. In single player mode, it behaves like an unused frame. The game state is
$08discussed in the sections “Creating Tetrimino” and “Choosing Tetrimino”. The game state is
$09not used. $0Bincreases the game state, but also looks unused. And now, finally, the main game loop:
; while(true) {
8138: JSR $8161 ; branchOnGameMode();
813B: CMP $00A7 ; if (vertical blanking interval wait requested) {
813D: BNE $8142 ; waitForVerticalBlankingInterval();
813F: JSR $AA2F ; }
8142: LDA $00C0
8144: CMP #$05
8146: BNE $815A ; if (gameMode == DEMO) {
8148: LDA $00D2
814A: CMP #$DF
814C: BNE $815A ; if (reached end of demo table) {
814E: LDA #$DD
8150: STA $00D2 ; reset demo table index;
8152: LDA #$00
8154: STA $00B2 ; clear upper byte of frame counter;
8156: LDA #$01
8158: STA $00C0 ; gameMode = TITLE_SCREEN;
; }
; }
815A: JMP $8138 ; }