Fluid Dynamics Simulation: Lattice Boltzmann Method

Modeling a volcanic eruption
using the Lattice Boltzmann Method. (c) Source

In this article I will talk about the numerical method for modeling the hydrodynamics of the Lattice Boltzmann Method , LBM. In Russian, the method of lattice Boltzmann equations. It surpasses other known methods (for example, finite element method ) in ease of parallelization, the ability to simulate multiphase flows, and to simulate flows in porous media. In addition, the computational algorithm contains only the simplest arithmetic operations. The method is very new, the first commercial products based on it began to appear around 2010.

There was already a series of articles on fluid physics at the hub, and this article may be its logical continuation. It is written in such a way as to be useful to people who know hydrodynamics and modeling methods well, and understandable to beginners in this field (for example, to people with a software engineer education). Of course, in this regard, many things will be too detailed for experts, and some will not have enough space. The article turned out to be quite large, but I would not want to break it into several parts.

Why is all this necessary? More precisely, in which industries it is necessary to simulate hydrodynamics:

aircraft construction, rocket science, automotive industry (body characteristics, engine operation, nozzles)
industrial chemistry (separation of substances, chemical reactors)
meteorology, geology (fluid flows through porous media, sandstones, dams)
other engineering industries (wind farms)
medicine (blood flow, lymph)

The article will include the following sections:

Physics Review - A High Level Review of Basic Essential Equations
The basic idea is a description of the basic principle of the algorithm
Technical Details — A more detailed explanation of the source equations, a computational scheme
- The Navier-Stokes equation
- Boltzmann equation
- Discrete Boltzmann Equation
- Computing diagram illustration
- Spatial gratings
- Equilibrium distribution functions
- Incompressibility
- Viscosity and Reynolds Number
- Once again, all together
miscellanea
- Algorithm Additions
- Underwater rocks
- Existing solutions
- What to read

Physics Overview

Hydro- and aerodynamics are macroscopically described by the Navier-Stokes equation . It shows what the pressure, density and velocity of the liquid will be at each point in space at each moment of time — depending on the initial and boundary conditions and the parameters of the medium.

On the other hand, for rarefied gases the Boltzmann equation is valid , which describes how the particle velocity distribution density at each point in space changes with time. If we integrate the particle velocity distribution at a given point, we can obtain the density and macroscopic velocity at a given point. In other words, macroscopically, the Boltzmann equation is equivalent to the Navier-Stokes equation.

main idea

Despite the fact that for dense liquids the Boltzmann equation is not applicable, if we learn to model it, we can also model the Navier-Stokes equation for these liquids. That is, we thereby replace the underlying level of abstractions (the microscopic equation for dense liquids) with a physically incorrect implementation (the microscopic equation for rarefied gases), but so that the upper level (the macroscopic Navier-Stokes equation) is described correctly.

The situation is illustrated in the picture below.
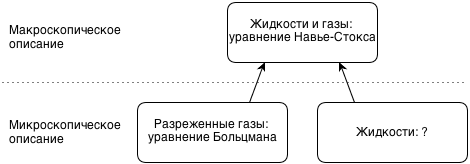
Idea of the Lattice Boltzmann Method

The question mark in it symbolizes the fact that I do not know which equation describes the behavior of dense liquids at the microscopic level. Sometimes they say “mesoscopic” instead of “microscopic” —in the sense that a microscopic description is a description of the behavior of individual atoms and molecules, and the Boltzmann equation describes the flows of molecules.

Since the computer does not know how to work with continuous quantities, we need to discretize the Boltzmann equation: in time, in spatial coordinates (we obtain spatial nodes for modeling) and in possible particle directions in each spatial node. Directions are selected in a special way, and always point to some neighboring nodes.

Technical details

This large section contains a more detailed explanation of the original equations and the derivation of a computational scheme. Really important equations should be clear to all readers with a technical background (the foundations of linear algebra, integral calculus are required). Those equations that are incomprehensible are most likely not important (these are those where there is a nabla ). Vectors are indicated in bold.

The Navier-Stokes equation

A variant of the equation for the macroscopic dynamics of incompressible liquids and gases looks like this:
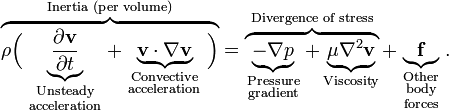The Navier-Stokes equation

(1)

here v is the flow velocity, ρ is the density of the fluid, p is the pressure in the fluid, f are external forces (for example, gravity).

If you don’t know what inverted triangles and partial derivatives are, don’t worry, we won’t need them in the future, and the computational algorithm contains only the simplest arithmetic operations.

A detailed conclusion and physical meaning can be studied on Wikipedia and Habré , but here I will give the main idea.

Mentally select a small volume in the liquid and trace its movement. The acceleration acting on a given volume of fluid is determined by (i) the pressures on the left, right, top, bottom, etc. (moreover, they partially compensate each other), (ii) by the action of internal friction forces in the fluid (iii) by external forces. On the other hand, acceleration can be expressed in terms of the difference in velocities at the initial time at the initial point and at some next point in time at that new point where the volume of liquid will be.

If we now substitute these quantities in the Newton equation F = ma, after simple transformations we get the equation above. On the left is ma, on the right is F.

Boltzmann equation

This equation operates with the distribution function of the probability density of particles along the coordinates and velocities, f (r, v, t). The value f (x, y, z, v _x , v _y , v _z , t) dx dy dz dv _x dv _y dv _z shows what fraction of particles at time t is in the cube from x to x + dx, from y to y + dy, from z to z + dz with speeds ranging from v _x to v _x + dv _x , from v _y to v _y + dv _y , from v _z to v _z + dv _z . It can also be written as f (r, v, t) d ^ 3r d ^ 3v

.

This function is typically normalized to the mass of gas in the system, so the macroscopic gas density at each point is determined as the sum (integral) of the probability density in a given point over all possible rate values
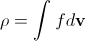Density

. (2)
Similarly, macroscopic velocity can be determined through

. (3)

The basic idea for deriving the equation is similar to the derivation of the Navier-Stokes equation. Let us mentally isolate at a given moment in a given small volume a beam of molecules flying in a given direction (more precisely, a narrow cone of directions). After a short period of time dt, they will be at a neighboring point (due to the presence of speed), their speed itself will change due to the acceleration of molecules by external forces. In addition, on this segment of the path, some molecules will collide with others, change their speed, and we will no longer be able to include them in the original beam. On the other hand, as a result of collisions of molecules in the same volume, flying in the opposite direction, some of them will acquire the desired direction of velocity, and we will add them to the beam.

This can be written as follows:,
$Boltzmann derivation, f \ left (\ mathbf {r} + \ mathbf {v} dt, \ mathbf {v} + \ frac {\ mathbf {F}} {m} dt, t + dt \ right) \, d ^ 3 \ mathbf {r} \, d ^ 3 \ mathbf {v} - f (\ mathbf {r}, \ mathbf {v}, t) \, d ^ 3 \ mathbf {r} \, d ^ 3 \ mathbf {v} = dN_ {coll}$ (4)
where F is the external force, m is the mass of the molecule, dN _{coll is the} change in the number of particles in the beam due to collisions.

As determined in general terms, the value of dN _coll will remain hidden from the reader. We need only its standard approximation — Batnagar-Gross-Crook (BGK). In this approximation, dN _coll is
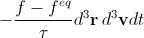$BGK approximation, - \ frac {f - f ^ {eq}} {\ tau} d ^ 3 \ mathbf {r} \, d ^ 3 \ mathbf {v} dt$ , (5)
where f ^{eq is the} equilibrium distribution function, the Maxwell-Boltzmann distribution , and τ is the so-called relaxation time .

As a result, we get
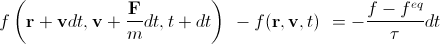$Boltzmann derivation, f \ left (\ mathbf {r} + \ mathbf {v} dt, \ mathbf {v} + \ frac {\ mathbf {F}} {m} dt, t + dt \ right) \ - f (\ mathbf {r}, \ mathbf {v}, t) \ = - \ frac {f - f ^ {eq}} {\ tau} dt$ . (6)
Note that f ^eqdepends on macroscopic density and velocity at a given point (that is, implicitly on coordinate and time). It is this equation that we will need in the future, but usually it is divided by dt and reduced to the form
$Boltzmann equation, \ frac {\ partial f} {\ partial t} + \ mathbf {v} \ cdot \ nabla f + \ frac {\ mathbf {F}} {m} \ cdot \ nabla _ {\ mathbf {v}} f = - \ frac {f- f ^ {eq}} {\ tau}$ , (7)
where nabla with index v is nabla with respect to speed variables.

Discrete Boltzmann Equation

In order to be able to simulate the dynamics of the continuous Boltzmann equation on a computer, we need to discretize it. To do this, we first introduce a uniform grid of spatial coordinates — let the grid step be the same along all axes. The behavior of the liquid will be determined precisely at the nodes of the grid. In fact, we allow molecules to be located only in certain spatial nodes. In addition, we must discretize the time — we will determine the state of the liquid at equal times from each other. In addition, we will allow molecules to have only certain velocity values — such that in a time step they manage to move to some neighboring node. These allowed directions will be the same for all spatial nodes. Obviously, in the diagonal directions the particle velocities will be greater,

Intuitively, we can conclude that with an infinitely small time step and a spatial lattice step, this discrete system will go over to the usual Boltzmann equation, which, in turn, will go over to the Navier-Stokes equation in the macroscopic limit. Oddly enough, this is not such a simple question, and we will postpone it for now.

In the further exposition, it is assumed everywhere that the system of units is such that the lattice step is a unit of length and the time step is a unit of time.

For simplicity, we will assume below that there are no external forces. We number the allowed speed directions from 1 to Q with the index i. If now the mass of particles flying from a given node in the direction i in a time step is denoted as f _i , then equation (6) will go to
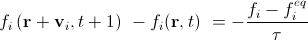$Discrete Boltzmann, f_i \ left (\ mathbf {r} + \ mathbf {v} _i, t + 1 \ right) \ - f_i (\ mathbf {r}, t) \ = - \ frac {f_i - f_i ^ {eq }} {\ tau}$ . (eight)
Here we took into account that the time step is equal to unity, and we replaced all dt from (6) by one. f _i^eq denotes the discrete equilibrium distribution density, which depends on the macroscopic mass and velocity at a given node. We did not indicate from which particular node we will use f _i^eq —from r + v _i t at time t + 1 or from r at time t. For the computational scheme, it turns out to be more convenient to use the node r + v _i t at time t + 1. Then the equation above can be decomposed into two components, the spreading step and the collision step.

Step the Streaming:
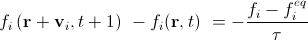$Streaming, \ tilde {f} _i \ left (\ mathbf {r} + \ mathbf {v} _i, t + 1 \ right) \ = f_i (\ mathbf {r}, t) \,$ . (9)
Collision step:
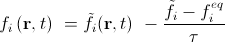$Collision, f_i \ left (\ mathbf {r}, t \ right) \ = \ tilde {f} _i (\ mathbf {r}, t) \ - \ frac {\ tilde {f} _i - f_i ^ {eq} } {\ tau}$ . (10)

Here f _iwith a tilde denotes the mass of particles arriving at a site in the direction i, but not yet colliding with the rest of the arriving particles. Streaming step is sometimes called an advection step.

For discretized directions of velocity, the mass and macroscopic velocity at each node will be calculated as
$Density and velocity discrete, \ rho = \ sum_ {i} f_i, \ rho \ mathbf u = \ sum_ {i} f_i \ mathbf v_i$ . (11)

Hereinafter, we write everywhere density instead of mass, because with a single spatial step of the lattice, a single volume is necessary for each node, and the mass and density coincide in value.

We show that the equilibrium distribution functions depend on the mass at the nodes and the macroscopic speed. Therefore, after the streaming step, it is necessary to recalculate the masses and velocities in each node, recalculate the equilibrium distribution functions, and then make a collision.

Thus, at each step of the computational scheme, it is necessary to “propagate” particles, that is, to move particles flying from node r in direction i to node r + v _i (do this for all particles and directions). After this, it is necessary to recalculate the masses, velocities, and equilibrium distribution functions. Finally, it is necessary to “collide” particles that have arrived at a given site — that is, to redistribute the particles in directions.

Computing diagram illustration

We illustrate the computational scheme with the example of a two-dimensional system. The discretization into spatial nodes and the relationships between them (that is, the allowed directions of speed) are depicted in the figure below. The spatial nodes are indicated by circles, the connections between them by thin lines.
D2Q9

The following figure shows one iteration of the streaming / collision pair. Colored arrows depict streams of flying molecules. The color intensity encodes the mass of molecules flying in a given stream, the length of the arrows approximately corresponds to the path traveled by the stream in a time step (only approximately, since the arrows should go from the center of the node to the center of the node).
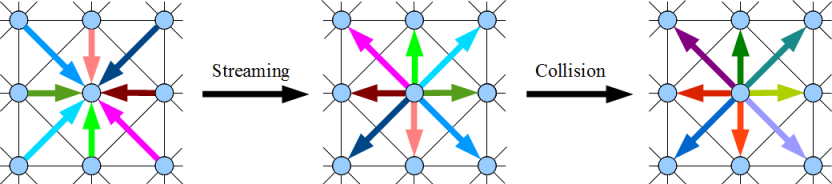
Collisionadvection

Spatial gratings

In LBM, lattice is a set of allowed velocity vectors (the same for each spatial node). This is consistent with the standard mathematical definition of a lattice as an entity, with the help of which by means of parallel transfers one can obtain the entire spatial grid.

In LBM, any lattice must contain a zero vector from a node to itself — it describes particles that do not fly anywhere from a given node. In LBM, lattices are usually denoted by the abbreviation DnQm, where n is the dimension of space, m is the number of vectors in the lattice. For example, D2Q9, D3Q19, etc.

In a two-dimensional LBM space, a lattice can consist, for example, of 5 vectors (2 vertical, 2 horizontal and zero vector from a node into itself), or it can consist of 9 vectors, as in the illustration above (2 vertical, 2 horizontal, 4 diagonal, one null). These are the D2Q5 and D2Q9 lattices, respectively.

Obvious factors for choosing lattices are: 1. simulation accuracy (intuitively, the more vectors in the lattice, the more accurate the simulation) 2. computational costs (calculation on the D2Q5 lattice will be faster than the calculation on D2Q9). Oddly enough, these are not the most important factors. The most important factors are the reproducibility of the Navier-Stokes equations and the symmetry of some tensors based on lattice vectors.

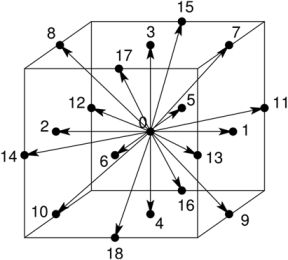
Commonly used grilles are D2Q9, D3Q15, D3Q19. The grilles D2Q9 and D3Q19 are shown below. The basic lattice vectors are usually denoted as e _i or c _i (they coincide with the velocities v _i introduced earlier at a unit time step). Below we will use the notation e _i .

D2Q9

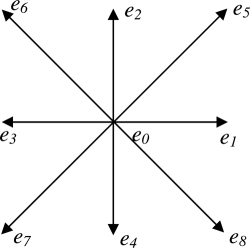
We write out the basis vectors for D2Q9:
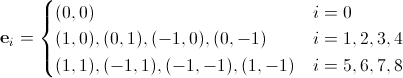$D2Q9 vectors \ bold {e} _i = \ begin {cases} (0,0) & i = 0 \\ (1,0), (0,1), (- 1,0), (0, -1) & i = 1,2,3,4 \\ (1,1), (- 1,1), (- 1, -1), (1, -1) & i = 5,6,7,8 \ \ \ end {cases}$ (11)

and for D3Q19:
$D3Q19 vectors \ bold {e} _i = \ begin {cases} (0,0,0) & i = 0 \\ (\ pm 1,0,0), (0, \ pm 1,0), (0, 0, \ pm 1) & i = 1,2, ..., 5,6 \\ (\ pm 1, \ pm 1,0), (\ pm 1,0, \ pm 1), (0, \ pm 1, \ pm 1) & i = 7.8, ..., 17.18 \\ \ end {cases}$ (12)

Once again, we recall that we always assume that the time step is equal to unity, therefore v _i = e _i .

Equilibrium distribution functions

In the continuous case, the equilibrium distribution function ( Maxwell-Boltzmann distribution ) is
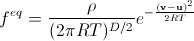$Maxwell distribution, f ^ {eq} = \ frac {\ rho} {(2 \ pi RT) ^ {D / 2}} e ^ {- \ frac {(\ bold {v} - \ bold {u}) ^ 2} {2RT}}$ . (13)

There are previously unknown quantities: R is the universal gas constant, T — temperature, D — dimension of space, v — velocity vector, the probability density for which we find. Here, the molar mass of gas is taken equal to unity (it is not important for us — only macroscopic density is important). We can consider this a change in the unit of mass in our simulation. In addition, the function is normalized to the local macroscopic density, and not to unity. We also note that usually the macroscopic velocity of gas u is not taken away from v. This is because the distribution is usually studied in the case of a stationary gas, but we need to go to a local inertial reference frame moving with the current gas velocity at a given point at a given time in order to use the Maxwell-Boltzmann distribution. Subtracting u is such a transition.

Suppose that at a given point in space, the distribution of molecules in velocity turned out to be equilibrium. This distribution depends on the macroscopic mass ρ and velocity u. On the other hand, we can calculate ρ and u from the distribution function (see formulas (2) and (3)). Obviously, this calculation should give the correct ρ and u (that is, in a sense, this is an additional restriction on the distribution function):
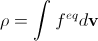$Density equilibrium, \ rho = \ int f ^ {eq} d \ mathbf v$ , $Velocity equilibrium, \ rho \ mathbf u = \ int f ^ {eq} \ mathbf vd \ mathbf v$ . (14)

The same requirements we impose on the calculation of the density and velocity in the discrete case:
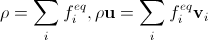$Density and velocity discrete equilibrium, \ rho = \ sum_ {i} f ^ {eq} _i, \ rho \ mathbf u = \ sum_ {i} f ^ {eq} _i \ mathbf v_i$ . (15)

The main requirement for discrete equilibrium distribution functions is the reproduction of the Navier-Stokes equation in the limit of infinitesimal time steps and lattice steps. This is equivalent to the fact that if for given ρ and u we try to calculate them again using the equilibrium distribution functions in the continuous and discrete cases, the results coincide (see the remark above that in the discrete case mass is meant instead of density), t. e.
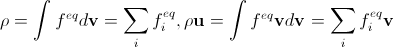$Density and velocity equality, \ rho = \ int f ^ {eq} d \ mathbf v = \ sum_ {i} f ^ {eq} _i, \ rho \ mathbf u = \ int f ^ {eq} \ mathbf vd \ mathbf v = \ sum_ {i} f ^ {eq} _i \ mathbf v$ . (16)

To uniquely determine the equilibrium discrete distribution function, we will also need to include a similar requirement for the equality of macroscopic thermal energies at a given point; we omit it for brevity.

If we summarize equation (10) for the collision step along the directions of velocity, then, taking into account formula (16), we can show that the collision step does not change the macroscopic masses and velocities of the molecules in the site.

It turns out that if we simply substitute the discrete velocity vectors e _i = v _i from (11) and (12) into the continuous equilibrium distribution function (13), equalities (16) will not hold.

It also turns out that we can make equalities (16) hold if we expand the Maxwell-Boltzmann distribution (13) in a Taylor series up to the second order of macroscopic speed. This corresponds to the fact that u / sqrt (RT) is very small. This restriction must always be satisfied during the simulation process at all nodes.

But even expanding into a Taylor series is not enough. We also need to introduce specially selected factors w _i into the discretized functions f _i^eq (details of the calculations can be found in this beautiful article — there is also a free version ; of course, everything will turn out to be a little more complicated than in our superficial description — in fact, the calculation happens through tensors, up to the fourth rank, built on lattice vectors). We finally get it . (17) There is a catch: we always assume that the lattice pitch and time are units of length and time, respectively. Therefore, we cannot take the value of R from SI, and the temperature here is not equal to the temperature of the simulated fluid in Kelvin.
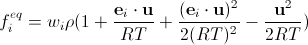
$Maxwell distribution discrete, f ^ {eq} _i = w_i \ rho (1+ \ frac {\ vec {v_i} \ cdot \ vec {u}} {RT} + \ frac {(\ vec {v_i} \ cdot \ vec {u}) ^ 2} {2 (RT) ^ 2} - \ frac {\ vec {u} ^ 2} {2RT})$

To determine their values, we note the following. Suppose there is a disturbance in the fluid — that is, in some nodes there is excess mass. This mass will begin to “spread” in space, moreover, in the rightmost node in the perturbation region, it will also move in the direction (1, 0, 0) in 3D or (1, 0) in 2D. For a unit of time, molecules along these directions will pass a unit of length, that is, their speed will be equal to unity. This means that the speed of sound as the speed of propagation of disturbances in our system is also equal to unity. On the other hand, the speed of sound is equal to sqrt (γ RT / μ), where γ is the adiabatic constant , μ is the molar mass, which we assumed to be equal to unity earlier. The adiabatic constant γ is 1 + 2 / d, where d is the number of degrees of freedommolecules. In an ideal gas, it is equal to the dimension of space. In our gas, molecules can only move along the straight lines connecting the nodes, so the dimension is not three (or two), but one. That is, γ = 3, and sqrt (3 RT) = 1.

Usually, in the literature on LBM, “speed of sound” is understood as a value
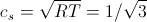$Speed of sound, c_s = \ sqrt {RT} = 1 / \ sqrt {3}$ . (18)

Now, finally
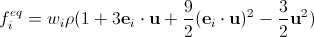$Maxwell distribution discrete, f ^ {eq} _i = w_i \ rho (1 + 3 \ mathbf {e} _i \ cdot \ mathbf {u} + \ frac {9} {2} (\ mathbf {e} _i \ cdot \ mathbf {u}) ^ 2- \ frac {3} {2} \ mathbf {u} ^ 2)$ . (19)

We write the values of the coefficients w _i for the most common lattices.
For D2Q9:
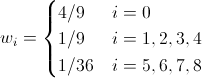$D2Q9 weights w_i = \ begin {cases} 4/9 & i = 0 \\ 1/9 & i = 1,2,3,4 \\ 1/36 & i = 5,6,7,8 \\ \ end {cases}$ (20)

For D3Q19:
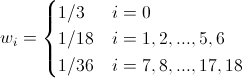$D3Q19 weights w_i = \ begin {cases} 1/3 & i = 0 \\ 1/18 & i = 1,2, ..., 5,6 \\ 1/36 & i = 7,8, ... , 17,18 \\ \ end {cases}$ (21)

Incompressibility

The restriction on a small macroscopic fluid velocity can now be written as
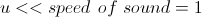$Incompressibility, u << speed \ of \ sound = 1$ . (22)

Recall that the Mach number is the ratio of the characteristic gas velocity in the system to the speed of sound. Then the restriction above corresponds to small Mach numbers or incompressible fluid. Indeed, if the speed of sound (the speed of propagation of density perturbations) is large, then any density perturbation will quickly spread to the entire system, and the density will again be the same. That is, you will not succeed in compressing the liquid in any one local area.

A good maximum value for the macroscopic velocity at the nodes will be, for example, 0.01.

Viscosity and Reynolds Number

The kinematic viscosity ν in LBM (as usual, in lattice units) is calculated as
$Viscosity, \ nu = (\ tau - 1/2) c ^ 2_s = (\ tau - 1/2) / 3$ . (23)
Here, τ is the relaxation time introduced earlier in formula (5), and _s = 1 / sqrt (3) is the “speed of sound” introduced in (18).

When modeling hydrodynamics without taking into account temperature changes, any system with a predetermined geometry (for example, a pipe with a square cross section) is completely described by only one dimensionless parameter — the Reynolds number equal to
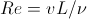$Reynolds, Re = v L / \ nu$ (24)
where v is the characteristic velocity in the system (for example, the velocity in the center of the pipe ), L is the characteristic length in the system (for example, the length of the side of a square section).

For standard geometries, the relationship between the characteristic velocity and the external force (which provides the flow) is usually known. Therefore, for modeling with a given Reynolds number, it is necessary

choose the characteristic speed v. As we found out, it should be much less than the speed of sound. For example, 0.01.
calculate the necessary external force for such a speed
calculate the viscosity according to (23) so as to obtain the desired Reynolds number
calculate the relaxation time from (24) so as to obtain the desired viscosity

If the simulation problem is compiled in SI units (supposedly, the side of the square pipe cross-section is 1 m, the pressure at the pipe inlet is X Pascals, at the outlet — Y Pascals), then first you need to find the dimensionless Reynolds number and use the algorithm above.

Once again, all together

Before modeling, it is necessary to set the initial macroscopic masses and velocities in each node. Then set the mass flows in each allowed direction e _i in each node (see Pitfalls). The easiest way is to indicate flows from the equilibrium distribution.

To simulate in a loop commit

streaming step by the formula (9)
recalculation of macroscopic masses and velocities in each node according to formulas (11), recalculation of equilibrium flows in all directions according to formula (19)
collision step by the formula (10)

Modeling usually occurs until the system is stationary. Stationarity can be checked, for example, through the difference in macroscopic velocities and masses in each node between adjacent steps, the maximum among all nodes.

miscellanea

Algorithm Additions

We did not touch on the inclusion of external forces in modeling (for example, gravity). They will lead to a small addition to equation (9) for the streaming step.

We also did not touch on the boundary conditions — on the surface of bodies and at the inlet and outlet of the system (for example, if a constant pressure or velocity field is specified at the inlet of the pipe). LBM has great freedom in modeling such conditions, since the method is formulated at the microscopic level (flows of molecules), and such boundary conditions are formulated at the macroscopic level. There are many ways to set boundary conditions at the microscopic level — and many algorithms .

The boundary conditions at the boundary of solids in hydrodynamics are usually chosen as no-slip boundary conditions (that is, when the fluid velocity on the surface of the bodies is zero). Usually they are realized through bounce-back conditions (when the flows of molecules are reflected in the opposite direction when crossing a solid wall). This can be read here , section 4.6.

The collision model that we introduced is called single relaxation time. There are more advanced models, for example, multiple relaxation time (in particular, double relaxation time).

LBM also supports multiphase (modeling the flow of a mixture of liquids or gases with different parameters).

The presence of thermal conductivity (that is, heat transfer in the system, changes in temperature at different points in the system and, as a result, changes in system parameters — for example, density) is also supported by LBM . The temperature is modeled as a separate "gas", also using the LBM algorithm, but the speed of this gas is determined by the speed of the main fluid. It is said that temperature in this sense is a passive scalar. There are many articles on modeling the Rayleigh – Benard convection phenomenon through the LBM .

We did not touch upon issues of effective implementation and parallelization at all.

Underwater rocks

If you model a system with thermal conductivity, then it will be described by two dimensionless quantities. In the case of Rayleigh-Benard convection, the Prandtl number and the Rayleigh number are usually chosen . In order to reproduce this system in lattice units, it is not enough just to reproduce both of these dimensionless quantities by correctly setting the internal parameters of the system (characteristic speed, external force, thermal conductivity). The fact is that hidden dependencies will exist between the internal parameters. Read more here .

As we have already said, when choosing the characteristic speed in the system, do not forget that the Mach number should be much less than unity (formula (22)).

LBM can become unstable in some systems at high Reynolds numbers (when the flow, however, is still laminar).

In LBM , Galilean invariance does not hold . However, this is usually not important.

At the beginning of the simulation, it is necessary to specify the flows of molecules from each node in all allowed directions. The equilibrium distribution of flows is often chosen (formula (19)). It is important to remember that equilibrium does not imply stationarity. That is, stationary distributions in the presence of gradients of speed, external force, etc. differ from equilibrium. Their calculation is given here (formulas 12, 19, 20 by reference).

Existing solutions

There is a large and very mature open-source project entirely dedicated to LBM— Palabos (PArallel LAttice BOLtzmann). The project also has a wiki . Developers provide paid advice on modeling hydrodynamics.

There are excellent tutorial examples of modeling typical systems on MATLAB. For example, Rayleigh – Benard convection (in the presence of external force, thermal conductivity, boundary conditions, correct translation of quantities). A total of 160 lines in MATLAB.

There are many commercial solutions, for example, this or that .

A detailed list of commercial and non-commercial LBM packages can be found on Wikipedia .

What to read

In addition to all the links that are in the article, you can recommend these lists of articles and books . Basically, a similar list of books is on Wikipedia .

That's all,

Thanks for attention!

Tags: