Something more complicated than factorial
Once upon a time, when the grass was greener and the trees taller, there lived a troll named Xenocephal. He lived, in principle, in many places, but I was lucky to meet him at one forum , where at that time I was gaining intelligence. I don’t remember the topic in which the conversation took place, but its essence was that Xenocephal tried to convince everyone around that Lisp (with its macros) was the head of everything, and C ++, with its templates, was a miserable semblance of a left hand. It was also argued that it was not possible to program something more complicated in it than was hard-pressed factorial .
I, in principle, had no objection that Lisp macros were prohibitively cool and, at that time, I had nothing to answer, but the phrase about C ++ templates and factorial deeply stuck in my fragile brain and continued to torment me from the inside out. And one terrible day, I thought: “What the hell ??? Let’s programm! ” The Dragon Book
was another source of inspiration . The task was found quickly. I found that the algorithm for converting a Nondeterministic State Machine ( NFA ) to a Determinant State Machine ( DFA ) is nontrivial enough to try to implement it using C ++ templates. The imperishable work of Alexandrescu allowed him to gain a critical mass ...
I began, of course, with primitives. I needed to somehow represent the graphs:
The arc of the graph was specified by the indices of the initial (Src) and final (Dst) vertices and could be named by the symbol (Chr). Unnamed arcs (used by the transformation algorithm) are, by default, marked with a null character. The Next type defined in this template turned it into a list of types. Adding an arc to this list was implemented in the following recursive manner:
Similarly, the merging of lists was organized (thanks to duck typing, any, and not just those that represent the graphs):
... and applying an arbitrary functor to each element of the list:
Now, it was necessary to implement the construction of the NCA based on the regular expression. The very technique of this construction is well described in the book mentioned above and boils down to the fact that the elements of the regular expression are replaced by some basic constructions connected by unnamed arcs.
A named arc is created in an elementary way:
The starting and ending vertices receive indices 0 and 1, respectively.
Two graphs can be connected in the alternative construction / A | B / as follows:
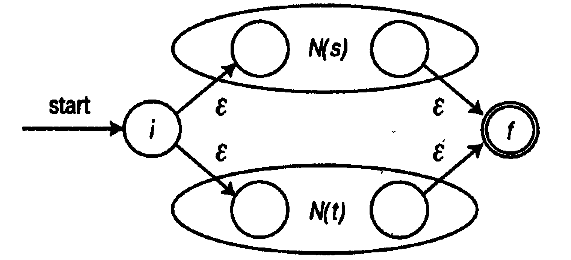
Here, we “merge” two input graphs (A and B) (while their vertices are renumbered), after which, we connect them with unnamed arcs, according to the diagram above. The starting and ending vertices still have indices 0 and 1, respectively.
The implementation of the following / AB / turned out to be somewhat more difficult to understand:
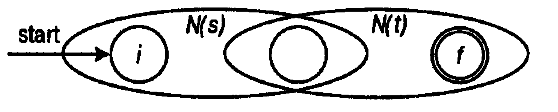
Here, additional arcs are not built, and the graphs are connected by a common vertex (initial for B and final for A).
The implementation of the quantifier / T * / turned out to be the most difficult:
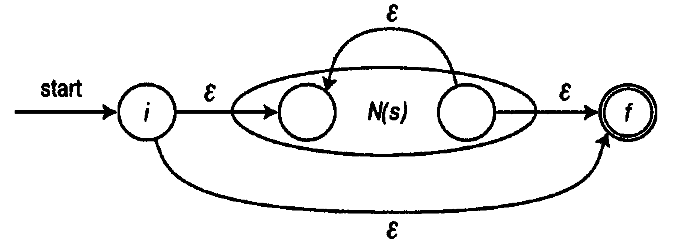
Since the quantifiers / T * / and / T + / are quite common, their optimized implementations were overloaded:
Now, it was possible to assemble an NFA representing the regular expression / (a | b) * abb / described in the book:
It remains to convert it to DKA:
I will not describe in detail all the ordeals associated with debugging this code (which cost only kilometer-long listings with compilation error messages), I only note that the front-end implementation of the algorithm hung the compiler completely, as a result of which I had to implement the optimized ImportantOpt template.
Now you can run the following code:
... and make sure that the result it produces is:
Corresponds to the desired column DKA:
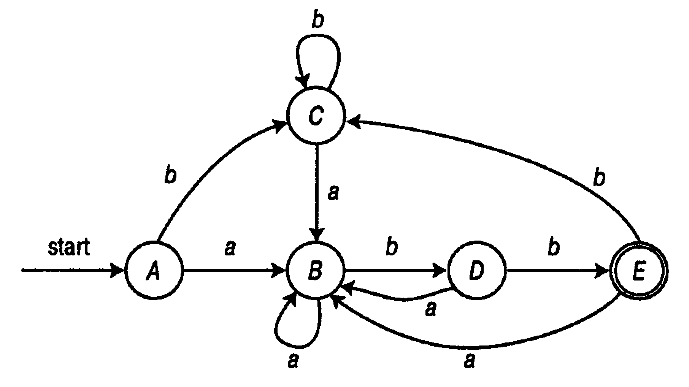
As usual, the sources are posted on GitHub .
I, in principle, had no objection that Lisp macros were prohibitively cool and, at that time, I had nothing to answer, but the phrase about C ++ templates and factorial deeply stuck in my fragile brain and continued to torment me from the inside out. And one terrible day, I thought: “What the hell ??? Let’s programm! ” The Dragon Book
was another source of inspiration . The task was found quickly. I found that the algorithm for converting a Nondeterministic State Machine ( NFA ) to a Determinant State Machine ( DFA ) is nontrivial enough to try to implement it using C ++ templates. The imperishable work of Alexandrescu allowed him to gain a critical mass ...
I began, of course, with primitives. I needed to somehow represent the graphs:
template
struct Edge
{ enum { Source = Src,
Dest = Dst,
Char = Chr
};
typedef T Next;
static void Dump(void) {printf("%3d -%c-> %3d\n",Src,Chr,Dst);T::Dump();}
};
The arc of the graph was specified by the indices of the initial (Src) and final (Dst) vertices and could be named by the symbol (Chr). Unnamed arcs (used by the transformation algorithm) are, by default, marked with a null character. The Next type defined in this template turned it into a list of types. Adding an arc to this list was implemented in the following recursive manner:
struct NullType {static void Dump(void) {printf("\n");}};
template struct AddEdge;
template struct AddEdge {
typedef typename Edge Result;
};
template struct AddEdge,R> {
typedef typename AddEdge::Result Result;
};
template
struct AddEdge,R> {
typedef typename AddEdge >::Result Result;
};
Similarly, the merging of lists was organized (thanks to duck typing, any, and not just those that represent the graphs):
Append
template struct Append;
template struct Append {
typedef T Result;
};
template
struct Append,B> {
typedef typename Append >::Result Result;
};
Join
template struct Join;
template struct Join {
typedef B Result;
};
template struct Join,B> {
typedef typename Join::Result>::Result Result;
};
template struct Join,B> {
typedef typename Join::Result>::Result Result;
};
template struct Join,B> {
typedef typename Join::Result>::Result Result;
};
template
struct Join,B> {
typedef typename Join::Result>::Result Result;
};
... and applying an arbitrary functor to each element of the list:
Map
template class F> struct Map;
template class F> struct Map {
typedef R Result;
};
template class F>
struct Map,V,R,F> {
typedef typename Map::Result,R>,F>::Result Result;
};
template class F>
struct Map,V,R,F> {
typedef typename Map::Result,F::Result,C>,F>::Result Result;
};
Now, it was necessary to implement the construction of the NCA based on the regular expression. The very technique of this construction is well described in the book mentioned above and boils down to the fact that the elements of the regular expression are replaced by some basic constructions connected by unnamed arcs.
A named arc is created in an elementary way:
C
template
struct C
{ typedef typename Edge Result;
enum {Count = 2};
};
The starting and ending vertices receive indices 0 and 1, respectively.
Two graphs can be connected in the alternative construction / A | B / as follows:

D
template
struct Add { enum { Result = X+N }; };
template
struct DImpl
{ private:
typedef typename Append<
typename Map::Result,
typename Map::Result
>::Result N0;
typedef typename Edge N1;
typedef typename Edge N2;
typedef typename Edge N3;
public:
typedef typename Edge Result;
enum {Count = A::Count+B::Count+2};
};
template
struct D: public DImpl > {};
template
struct D: public DImpl {};
Here, we “merge” two input graphs (A and B) (while their vertices are renumbered), after which, we connect them with unnamed arcs, according to the diagram above. The starting and ending vertices still have indices 0 and 1, respectively.
The implementation of the following / AB / turned out to be somewhat more difficult to understand:

E
template
struct ConvA { enum { Result = (X==1) ? (X+N-1) : X }; };
template
struct ConvB { enum { Result = (X==1) ? 1 : (X+N) }; };
template
struct EImpl
{ private:
typedef typename Map::Result A1;
typedef typename Map::Result B1;
public:
typedef typename Append::Result Result;
enum {Count = A::Count+B::Count};
};
template
struct E: public EImpl > {};
template
struct E: public EImpl {};
Here, additional arcs are not built, and the graphs are connected by a common vertex (initial for B and final for A).
The implementation of the quantifier / T * / turned out to be the most difficult:

Q
template struct Q {
Q() {STATIC_ASSERT(Min<=Max, Q_Spec);}
private:
typedef typename Map::Result A1;
typedef typename Map::Result,T::Count,NullType,ConvB>::Result B1;
public:
typedef typename Edge::Result,0,T::Count> Result;
enum {Count = T::Count+Q::Count};
};
template struct Q
{ private:
typedef typename Map::Result A1;
typedef typename Map::Result, T::Count, NullType, ConvB>::Result B1;
public:
typedef typename Append::Result Result;
enum {Count = T::Count+Q::Count};
};
Since the quantifiers / T * / and / T + / are quite common, their optimized implementations were overloaded:
Q
template struct Q: public T {};
template
struct Q
{ private:
typedef typename Edge::Result,0,2> N0;
typedef typename Edge N1;
typedef typename Edge N2;
public:
typedef typename Edge Result;
enum {Count = T::Count+2};
};
template
struct Q
{ public:
typedef typename Edge Result;
enum {Count = T::Count};
};
template
struct Q
{ public:
typedef typename Edge Result;
enum {Count = T::Count};
};
Now, it was possible to assemble an NFA representing the regular expression / (a | b) * abb / described in the book:
typedef E< Q< D< C<'a'>, C<'b'> > >, C<'a'>, C<'b'>, C<'b'> >::Result G;
It remains to convert it to DKA:
DFA
enum CONSTS {
MAX_FIN_STATE = 9
};
template class DFAImpl;
template
class DFAImpl >: public DFAImpl
{ public:
typedef typename DFAImpl::ResultType ResultType;
ResultType Parse(char C)
{
if ((State==Src)&&(C==Chr)) {
State = Dst;
if (State::Parse(C);
}
void Dump(void) {T::Dump();}
};
template <>
class DFAImpl
{ public:
DFAImpl(): State(0) {}
enum ResultType {
rtNotCompleted = 0,
rtSucceed = 1,
rtFailed = 2
};
ResultType Parse(char C)
{ State = 0;
return rtFailed;
}
protected:
int State;
};
// Вычисление хода (списка состояний) из вершины (При a==0 - e-ход)
// N - Узел
// T - Граф
// R - Результирующее состояние
// a - Символ алфавита
template struct Move;
template struct Move {typedef R Result;};
template struct Move,R,a>
{ typedef typename Move::Result,a>::Result Result;
};
template
struct Move,R,a>
{ typedef typename Move::Result Result;
};
// Фильтрация списка по условию F
// T - Исходный список (Set, StateListEx)
// С - Значение параметра предиката F
// R - Результирующий список (Set, StateListEx)
// F - Предикат (Exist, NotExist, Important)
template class F> struct Filter;
template class F>
struct Filter {typedef R Result;};
template class F>
struct Filter,C,R,F>
{ typedef typename If::Result,
typename Filter,F>::Result,
typename Filter::Result
>::Result Result;
};
template class F>
struct Filter,C,R,F>
{ typedef typename If::Result,
typename Filter,F>::Result,
typename Filter::Result
>::Result Result;
};
// Вычисление e-замыкания
// T - Начальный список узлов
// G - Граф
// R - Результирующий список узлов
template struct EClos;
template struct EClos {typedef R Result;};
template
struct EClos,G,R>
{ private:
typedef typename Move::Result L;
typedef typename Filter::Result,NullType,NotExist>::Result F;
public:
typedef typename EClos::Result,G,
typename Set
>::Result Result;
};
// Вычисление хода из множества вершин
// T - Состояние
// G - Граф
// R - Результирующее состояние
// a - Символ алфавита
template struct MoveSet;
template struct MoveSet {typedef R Result;};
template
struct MoveSet,G,R,a>
{ typedef typename MoveSet::Result>::Result,a>::Result Result;
};
// Вычисление списка состояний, полученных всеми ходами из вершины
// N - Генератор номеров узлов
// K - Генератор номеров финальных узлов
// T - Алфавит
// n - Текущий узел
// S - Текущее состояние (Set)
// G - Граф
// R - Результирующий список расширенных состояний
template struct MoveList;
template
struct MoveList {typedef R Result;};
template
struct MoveList,n,S,G,R>
{ private:
typedef typename MoveSet::Result S0;
typedef typename EClos::Result S1;
enum { N1 = (NotExist<1,S1>::Result)?K:N };
public:
typedef typename MoveList<(N==N1)?(N+1):N,
(K==N1)?(K+1):K,
T,n,S,G,
StateListEx >::Result Result;
};
// Построение алфавита языка по графу NFA (вычислять однократно на верхнем уровне)
// T - Граф
// R - Результирующий алфавит
template struct Alf;
template struct Alf {typedef R Result;};
template struct Alf,R> {
typedef typename Alf::Result Result;
};
template struct Alf,R>{
typedef typename Alf::Result>::Result Result;
};
// Инкремент генератора узлов
// T - Список состояний (StateListEx)
// R - Результирующее значение генератора
// F - Предикат (Exist, NotExist)
template class F> struct Incr;
template class F>
struct Incr {enum {Result = R};};
template class F>
struct Incr,R,F>
{ enum { Result = Incr::Result)?((N>=R)?(N+1):R):R, F>::Result};
};
// Определение значимого узла
// N - Узел
// G - Граф
template struct Important;
template struct Important {enum {Result = (N==1)};};
template
struct Important > {
enum { Result = Important::Result };
};
template
struct Important > {
enum {Result = true};
};
template
struct Important > {
enum { Result = Important::Result };
};
// Оптимизированное построение списка значимых узлов
// T - Граф
// R - Результирующий список
template struct ImportantOpt;
template struct ImportantOpt {
typedef typename AddSet<1,R,NullType>::Result Result;
};
template
struct ImportantOpt,R>{
typedef typename ImportantOpt::Result Result;
};
template
struct ImportantOpt,R> {
typedef typename ImportantOpt::Result>::Result Result;
};
// Сравнение состояний по совокупности значимых узлов
// A - Список узлов (Set)
// B - Список узлов (Set)
// G - Граф
// I - Список значимых узлов (вычислять однократно на верхнем уровне)
template struct EquEx
{ private:
typedef typename Filter::Result A1;
typedef typename Filter::Result B1;
public:
enum { Result = Equ::Result };
};
template struct EquExOpt
{ private:
typedef typename Filter::Result A1;
typedef typename Filter::Result B1;
public:
enum { Result = Equ::Result };
};
// Получение списка узлов
// G - Граф
// R - Результирующий список
template struct EdgeList;
template
struct EdgeList {typedef R Result;};
template
struct EdgeList,R>
{ private:
typedef typename AddSet::Result R0;
typedef typename AddSet::Result R1;
public:
typedef typename EdgeList::Result Result;
};
// Проверка вхождения (по равенству состояний)
// T - Контрольный список (StateList)
// S - Искомое состояние (Set)
// I - Список значимых узлов
template struct ExistS;
template
struct ExistS {enum {Result = false};};
template
struct ExistS,S,I>
{ enum { Result = (Equ::Result) ? // EquExOpt::Result
true :
ExistS::Result
};
};
// Отброс ранее найденных узлов
// T - Исходный список (StateListEx)
// С - Контрольный список (StateList)
// I - Список значимых узлов (Set)
// R - Результирующий список (StateListEx)
template struct FilterT;
template
struct FilterT {typedef R Result;};
template
struct FilterT,C,I,R>
{ typedef typename If::Result,
typename FilterT::Result,
typename FilterT >::Result
>::Result Result;
};
// Формирование результирующего графа
// T - Множество ранее сформированных вершин (StateList)
// a - Символ перехода к искомой вершине
// S - Исходное состояние (Set)
// I - Список значимых узлов
// R - Формируемый граф
template struct GenImpl;
template
struct GenImpl {typedef R Result;};
template
struct GenImpl,Src,Dst,a,S,I,R>
{ typedef typename If::Result, // EquExOpt
Edge,
typename GenImpl::Result
>::Result Result;
};
// Формирование результирующего графа
// T - Множество новых узлов
// С - Ранее сформированные узлы
// I - Множество значимых узлов
// R - Результирующий граф
template struct Gen;
template
struct Gen {typedef R Result;};
template
struct Gen,C,I,R> {
typedef typename Gen::Result>::Result Result;
};
// Шаг преобразования
// N - Генератор номеров результирующих узлов
// K - Генератор номеров финальных узлов
// G - Граф (NFA)
// A - Алфавит (Set)
// I - Список значимых узлов (Set)
// R - Результирующий граф (DFA)
// M - Список помеченных состояний (StateList)
// D - Список непомеченных состояний (StateListEx)
template struct ConvertImpl;
template
struct ConvertImpl {typedef R Result;};
template
struct ConvertImpl >
{ private:
typedef typename MoveList::Result T;
typedef typename StateList M1;
typedef typename Append::Result MD;
typedef typename FilterT::Result T1;
typedef typename AppendSafe::Result D1;
typedef typename Gen::Result,I,R>::Result R1;
enum { N1 = Incr::Result,
K1 = Incr::Result
};
public:
typedef typename ConvertImpl::Result Result;
};
// Преобразование NFA -> DFA
// G - Граф
// R - Результирующий граф
template struct Convert
{ private:
typedef typename Alf::Result A;
typedef typename ImportantOpt::Result I;
public:
typedef typename ConvertImpl<1,MAX_FIN_STATE+1,G,A,I,NullType,NullType,
StateListEx<0,0,0,typename EClos,G,NullType>::Result,NullType> >::Result Result;
};
template
class DFA: public DFAImpl::Result> {};
I will not describe in detail all the ordeals associated with debugging this code (which cost only kilometer-long listings with compilation error messages), I only note that the front-end implementation of the algorithm hung the compiler completely, as a result of which I had to implement the optimized ImportantOpt template.
Now you can run the following code:
typedef E< Q< D< C<'a'>, C<'b'> > >, C<'a'>, C<'b'>, C<'b'> >::Result G;
typedef Convert::Result R;
R::Dump();
... and make sure that the result it produces is:
1 -a-> 10
1 -b-> 11
13 -a-> 10
13 -b-> 1
10 -a-> 10
10 -b-> 13
11 -a-> 10
11 -b-> 11
0 -a-> 10
0 -b-> 11
Corresponds to the desired column DKA:

As usual, the sources are posted on GitHub .
