Population algorithm based on the behavior of a school of fish
Within the framework of this community, genetic algorithms and their application in practice have been repeatedly discussed. In this article, I would like to share a relatively new method of optimizing functions based on the behavior of a school of fish in search of food.
Since the middle of the last century, studies have been conducted to simulate the biological mechanisms of nature, in particular, related to the process of evolution. Only by the 80s, practical testing of these methods began in connection with the need for effective ways to optimize n-ary functions that have high computational complexity, multi-extremity, etc. Speaking of terminology, it is worth mentioning that these algorithms belong to the class of stochastic search engines. In many sources, one can also find definitions such as behavioral, intellectual, metaheuristic or population . We will use the latter term to classify our algorithm. Generally speaking, this algorithm can be determined more accurately using the following scheme.
Population algorithms are divided into the following categories:
Having dealt with the terminology, we proceed directly to the study of the population optimization algorithm based on the behavior of the school of fish.
This algorithm was proposed in 2008 by Filo (B. Filho) and Neto (L. Neto).
As in all population algorithms, the following parameters are set as input parameters: the fitness function (a function for which it is necessary to find extrema), the field of study of this function, and the parameters of the algorithm (more about them later). In the current FSS algorithm ( F ish S chool S earch), the search area is an aquarium in which agents (fish) swim. As you know, in the search for food, fish swim in a joint, so in our case the ultimate goal is to shift all agents to the extremum of the function. In general, the algorithm operation scheme is as follows:
The stage "Migration of agents" is performed iteratively, and in each of the iterations the operators of two groups are executed:
It is time to talk about the parameters that the aquarium and its inhabitants have.
So, we introduce the following variables that are characteristic of the whole aquarium as a whole:
These are the very parameters that the user enters. Using them, the ratio of accuracy / runtime of the algorithm is regulated .
The agents themselves are characterized by only two values:
Of course, with a software implementation of the algorithm, such a number of variables is clearly not enough, but for now we will not complicate our lives .
Realizing that code is more important to programmers than idle chatter, we will delve into the algorithm using the following pseudocode:
Note: all of the following explanations of the algorithm are designed to solve the problem of conditional maximization of a function, but this should not cause doubts about the inoperability of this method when searching for minimum values of a function.
This algorithm formed the basis of my course work (“Optimization program inspired by the behavior of a school of fish”), which was presented at the defense on April 26. Perhaps someone will be interested in why term papers were so early. Without further ado, I’ll just say that this is all part of the plan for expelling students from the 1st year of the Faculty of Biology (PI) of the Higher School of Economics, who were in the clutches of the educational unit, which threatens with a 30% deduction all year (on the back of the coin the propaganda slogan flaunts: “We will accept everyone, and if necessary, we will pay for the seats at our own expense”). As part of the course work, the implementation was conducted in C # 4.0, the OpenTK library (representing the OpenGL wrapper for .NET) was selected as the graphic component, the user-defined functions were parsed using the library,implemented on a habr earlier . Unfortunately, I can’t lay out the sources (the code is far from perfect, I realized it many times myself), but I will provide the program itself at the general discretion (links at the end of the article). In the meantime, just a screenshot of the main window:
For population-based algorithms, testing is a fascinating thing, because the result of its work largely depends on the input parameters. As part of this article, we will consider the following 2 graphs.
Thanks for reading the article! I will be happy to answer your questions in the comments.
UPD: Added source codes.
Introduction
Since the middle of the last century, studies have been conducted to simulate the biological mechanisms of nature, in particular, related to the process of evolution. Only by the 80s, practical testing of these methods began in connection with the need for effective ways to optimize n-ary functions that have high computational complexity, multi-extremity, etc. Speaking of terminology, it is worth mentioning that these algorithms belong to the class of stochastic search engines. In many sources, one can also find definitions such as behavioral, intellectual, metaheuristic or population . We will use the latter term to classify our algorithm. Generally speaking, this algorithm can be determined more accurately using the following scheme.
Population algorithms are divided into the following categories:
- Evolutionary algorithms, including the very genetic ones.
- Algorithms inspired by wildlife (for example, an algorithm for optimizing a swarm of fireflies, cuckoo search, etc.).
- Algorithms inspired by inanimate nature (for example, the gravitational search algorithm).
- Algorithms based on the behavior of human society (for example, an algorithm for the evolution of the mind).
- Other algorithms.
Having dealt with the terminology, we proceed directly to the study of the population optimization algorithm based on the behavior of the school of fish.
Algorithm parsing
This algorithm was proposed in 2008 by Filo (B. Filho) and Neto (L. Neto).
As in all population algorithms, the following parameters are set as input parameters: the fitness function (a function for which it is necessary to find extrema), the field of study of this function, and the parameters of the algorithm (more about them later). In the current FSS algorithm ( F ish S chool S earch), the search area is an aquarium in which agents (fish) swim. As you know, in the search for food, fish swim in a joint, so in our case the ultimate goal is to shift all agents to the extremum of the function. In general, the algorithm operation scheme is as follows:
- Initialization of the population (even distribution of fish in the aquarium)
- Migration of agents to a food source (analogy: the greater the step the agents took in the direction of the extremum of the function, the more food they received)
- Search completion
Need more details.
The stage "Migration of agents" is performed iteratively, and in each of the iterations the operators of two groups are executed:
- Swimming operators providing agents for migration within the aquarium.
- Feeding operators that record the success of the study of certain areas of the aquarium.
It is time to talk about the parameters that the aquarium and its inhabitants have.
So, we introduce the following variables that are characteristic of the whole aquarium as a whole:
populationSize- population size (number of fish in the school). iterationCount- the number of iterations in the stage "Migration of agents" lowerBoundPoint, higherBoundPoint- the upper and lower boundaries of the search individStepStart, individStepFinal- sets the initial and final radius of the food search around the agents weightScale- the maximum weight of the agent. These are the very parameters that the user enters. Using them, the ratio of accuracy / runtime of the algorithm is regulated .
The agents themselves are characterized by only two values:
swimStatePos- the position of the agent in different stages of swimming weight- the current weight of the agentOf course, with a software implementation of the algorithm, such a number of variables is clearly not enough, but for now we will not complicate our lives .
Realizing that code is more important to programmers than idle chatter, we will delve into the algorithm using the following pseudocode:
initialize_randomly_all_fish;
while (stop_criterion is not met)
{
for (each_fish)
{
individual_movement;
evaluate_fitness_function;
}
feeding_operator;
for (each_fish)
instinctive_movement;
calculate_barycentre;
for (each_fish) do
{
volitive_movement;
evaluate_fitness_function;
}
update_individidual_step;
}
Note: all of the following explanations of the algorithm are designed to solve the problem of conditional maximization of a function, but this should not cause doubts about the inoperability of this method when searching for minimum values of a function.
- So, as already mentioned, the first step is to initialize the entire population: randomly select the position of the agent within the aquarium (
swimStatePos[0]) and set the weight equal to half of the maximum (weight=weightScale/2) for all fish. - Next, the main cycle of the algorithm begins, which characterizes the stage of “Migration of agents to the food source”. In our case, the quantity “Iterations number” (
iterationCount) is used as a stopping criterion . - Then comes the individual stage of swimming agents. It is characterized by the fact that all the fish in a certain area around themselves (
individStep) try to find the best value of the function.
If they succeed, then this step is fixed. Otherwise,
we believe that this movement was not. - Now you need to consolidate the success in the individual stage of swimming. To do this, use the characteristic "Weight". It is the change in fitness function for this agent before and after the individual stages, the normalized maximum change in function among the population:
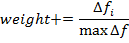. Generally speaking, this is a distinctive feature of this algorithm, since we do not need to remember the best agents in previous iterations. - After this, the fish make the next stage of swimming - instinctively collective. For the entire school of fish is calculated value of the "total migration step":
.
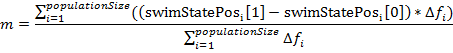Its meaning is as follows: each agent is affected by the whole population as a whole, while the influence of an individual agent is proportional to its success in the individual swimming stage. Then the whole population is shifted by the calculated value m: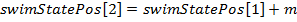
- Before the next sailing operation must perform intermediate steps, namely to calculate the center of gravity of the jamb:
. - We, or rather, fish, went to the last stage of swimming: collective-willful. Here you need to find out how the weight of the population has changed compared to the previous iteration. If it has increased, then the population has approached the area of maximum function, therefore, it is necessary to narrow the circle of its search, thereby intensifying properties are manifested . And vice versa: if the weight of the jamb has decreased, then the agents are looking for the maximum in the wrong place, so you need to change the direction of the trajectory and show diversification properties.
The valuecollStepin the following formula is responsible for the step of volitional bias. It is recommended to use a value 2 times larger than an individual search step. The operatordistcalculates the distance between two points in Euclidean space.
( The values responsible for the position of the agents are structural types of an n-dimensional point, for which the following operations are defined: addition / subtraction of two points, addition / subtraction of a point and a number, multiplication / division of a point and a number, and also operations of comparing points. To avoid of this geometric nonsense, it is customary to consider these quantities as vector data types, having defined certain operations ) - The last operator in the iteration is a linear decrease in the individual search step for the next iteration. In fact, this is already a modification of the standard FSS algorithm to increase the search efficiency, which is performed by the following formula:
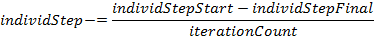
Implementation and testing
Implementation
This algorithm formed the basis of my course work (“Optimization program inspired by the behavior of a school of fish”), which was presented at the defense on April 26. Perhaps someone will be interested in why term papers were so early. Without further ado, I’ll just say that this is all part of the plan for expelling students from the 1st year of the Faculty of Biology (PI) of the Higher School of Economics, who were in the clutches of the educational unit, which threatens with a 30% deduction all year (on the back of the coin the propaganda slogan flaunts: “We will accept everyone, and if necessary, we will pay for the seats at our own expense”). As part of the course work, the implementation was conducted in C # 4.0, the OpenTK library (representing the OpenGL wrapper for .NET) was selected as the graphic component, the user-defined functions were parsed using the library,implemented on a habr earlier . Unfortunately, I can’t lay out the sources (the code is far from perfect, I realized it many times myself), but I will provide the program itself at the general discretion (links at the end of the article). In the meantime, just a screenshot of the main window:
Testing
For population-based algorithms, testing is a fascinating thing, because the result of its work largely depends on the input parameters. As part of this article, we will consider the following 2 graphs.
- Search scope: from (-100; -100) to (100; 100)
- Number of iterations: 100
- Population size: 50
- Initial Individual Step: 10
- Final Individual Step: 0.1
- Maximum fish weight: 50
So, by the end of the algorithm, the maximum value of the function was 9.999978 ..., and the average value is 9.999148 ... The graph of the average value is as follows: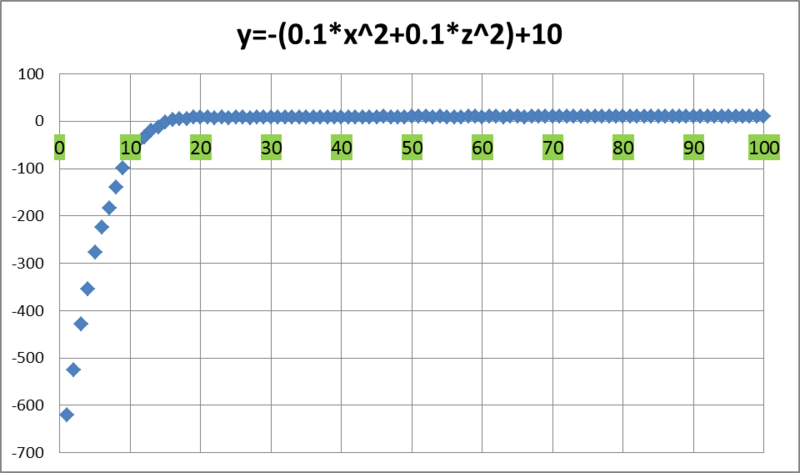
That is, at the 15th iteration, the school of fish was in the positive half-plane along the OY axis. And starting from the 48th iteration, the average value of the function did not fall below 9. And here is the full picture of what is happening (view from the tip of the iceberg):
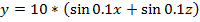
- Search scope: from (-100; -100) to (100; 100)
- Number of iterations: 100
- Population size: 50
- Initial Individual Step: 10
- Final Individual Step: 0.1
- Maximum fish weight: 50
By the end of the algorithm, the maximum value of the function was 19.999996 ..., and the average is 19.9994 ... The dynamics of the average value is as follows:
Already from 42 iterations, the average value of the function remained at the level of at least 19. Animation of how the algorithm copes with multi-extreme functions (for Habrastorage the file is too large, so there may be problems with the image display):
Sources
- You can download the program here (the kit includes: a program for studying functions of two variables with reports on functions from this article, a console version of the program with built-in functions of N variables, a description of the language for setting fitness functions (according to GOST, by the way))
- Perhaps the only Russian-language article in which this algorithm is described: A. Karpenko, “Population Algorithms for Global Search Engine Optimization. Overview of new and little-known algorithms. " Download .
- Website entirely dedicated to Fish School Search
- And another useful article in English
- Sources of the console version of the program (you can fork)
PS
Thanks for reading the article! I will be happy to answer your questions in the comments.
UPD: Added source codes.