Briefly about hydrodynamics: equations of motion
Having written the previous post , historical and partly advertising (although potential applicants are unlikely to read this), we can proceed to the conversation “in essence”. Unfortunately, a high degree of popularity of the description is unlikely to be achieved, but still I will try not to arrange a course of dry lectures. Although, it was not possible to get rid of dryness, and the post was written as a result exactly a month.
This publication describes the basic equations of motion for an ideal and viscous fluid. If possible, their conclusion and physical meaning are briefly reviewed, and several simple examples of their exact solutions are described. Alas, these few examples of analytically available solutions of the Navier-Stokes equations are largely exhausted. Let me remind you that the Clay Institute attributed the proof of the existence and smoothness of solutions to the problems of the millennium. Geniuses of Perelman level and above - the task awaits you.
In, so to speak, “traditional” hydrodynamics, which has developed historically, the foundation is a model of a continuous medium. It is distracted from the molecular structure of the substance, and describes the medium by several continuous field quantities: density, velocity (determined through the total momentum of the molecules in a given volume element) and pressure. The model of a continuous medium assumes that in any infinitesimal volume there are still quite a lot of particles (as they say, there are a lot of thermodynamically - numbers that are close in order of magnitude to the Avogadro number - 10 23 pieces). Thus, the model is limited from below by the discreteness of the molecular structure of the liquid, which is completely insignificant in problems of typical spatial scales.
However, this approach allows us to describe not only water in a test tube or reservoir, and is much more universal. Since our Universe is practically homogeneous on a large scale, then, oddly enough, starting from a certain scale it is perfectly described as a continuous medium, taking into account, of course, self-gravity.
Other, more mundane applications of a continuous medium are the description of the properties of elastic bodies, plasma dynamics, bulk solids. You can also describe people’s topl as a compressible fluid.
In parallel with the approximation of a continuous medium, a kinetic model based on the discretization of the medium into small particles interacting with each other (in the simplest case, like solid balls repelling in a collision) is gaining momentum in recent years. This approach arose primarily due to the development of computer technology, however, it did not bring substantially new results into pure hydrodynamics, although it turned out to be extremely useful for problems of plasma physics, which at the micro level is not homogeneous, but contains electrons and positively charged ions. Well, again, to simulate the universe .

The most elementary law. Suppose we have some completely arbitrary, but macroscopic volume of fluid V , bounded by surface F (see. Fig.). The mass of fluid inside it is determined by the integral:

And let nothing happen to the liquid inside it, except for movement. That is, there are no chemical reactions and phase transitions, no tubes with pumps or black holes. Well, everything happens at low speeds and for small masses of matter, therefore no theory of relativity, curvature of space, self-gravity of a liquid (it becomes significant on a stellar scale). And let the volume itself and its borders are motionless. Then the only thing that can change the mass of liquid in our volume is its flow through the boundary of the volume (for definiteness, let the mass in the volume decrease):

where vector j is the flow of matter through the boundary. The point, we recall, is the scalar product. Since the boundaries of the volume, as was said, are fixed, the time derivative can be introduced under the integral. And the right-hand side can be transformed to the same as on the left, volume integral by the Gauss-Ostrogradsky theorem .
As a result, in both sides of the equality we obtain an integral over the same completely arbitrary volume, which allows us to equate the integrands and go over to the differential form of the equation:

Here (and hereinafter) the Hamilton vector operator is used. Figuratively speaking, this is a conditional vector whose components are differentiation operators with respect to the corresponding coordinates. With its help, one can very briefly denote various kinds of operations on scalars, vectors, tensors of higher ranks and other mathematical evil spirits, the main ones being gradient , divergence and rotor . I will not dwell on them in detail, since this distracts from the main topic.
Finally, the flow of matter is equal to the mass transferred through the unit area per unit time:

Finally,the mass conservation law (also called the continuity equation) for a continuous medium is as follows:

This expression is the most general for a medium with a variable density. In reality, the experiment indicates an extremely weak compressibility of the liquid and an almost constant value of the density, which allows us to apply the law of mass conservation in the form of an incompressibility condition with high accuracy:

which works with no less good accuracy for gases, while the flow velocity is low compared to the sound velocity.
The whole relatively cumbersome process ofwitchcraft transforming the integrals used above gives us not only the continuity equation. Exactly the same essentially transformations allow expressing the laws of conservation of momentum and energy, and in the end to obtain equations for the velocity of a liquid and for heat transfer in it. However, for now, we will not rush much, and we will not just preserve the momentum, but even preserve the momentum in an ideal incompressible fluid - i.e. consider a model with a complete lack of viscosity.
The reasoning is practically the same, only now we are not interested in mass, and the total momentum of the fluid in the same volume of the V . It is equal to:

Under the same conditions as above, the momentum in the volume can change due to:
The corresponding integrals (the order corresponds to the list) give the following relationship:

We begin to transform them. True, for this you need to use tensor analysis and rules for working with indexes. More specifically, the Gauss-Ostrogradsky theorem is applied to the first and second integrals in a generalized form (it works not only for vector fields). And if we go to the differential form of the equation, we get the following: A

cross in a circle denotes a tensor product , in this case, vectors.
In principle, this is already the Euler equation, but it can be simplified a little - after all, the law of conservation of mass has not been canceled. Having opened the brackets in the differential operators here and then citing similar terms, we will see that the three terms are safely collected inthe continuity equation , and therefore give a total of zero. The final equation turns out to be this:

If we move to a reference frame connected with a moving fluid (we will not focus on how this is done), we will see that the Euler equation expresses Newton’s second law for a unit volume of the medium.
An ideal fluid, of course, is good (although it still cannot be solved for sure), but in many cases viscosity accounting is necessary. Even in the same convection, during the flow of fluid through pipes. Without viscosity, water would flow out of our cranes at cosmic speeds, and the slightest temperature heterogeneity in the water would lead to its extremely rapid and rapid mixing. Therefore, let's take into account the resistance of the liquid to itself.
The Euler equation can be supplemented by various (but equivalent, of course) ways. We will use the basic technique of tensor analysis — the index form of writing the equation. And while we also discard external forces, so as not to get confused under the arms / under the legs / in front of the eyes (underline as necessary). In this situation, everything except the time derivative can be collected in the form of a divergence of one such tensor:

In meaning, this is the momentum flux density in a liquid. It is necessary to add viscous forces to it in the form of another tensor term. Since they clearly lead to a loss of energy (and momentum), they must be subtracted:

Going back to the equation with such a tensor, we get a generalized equation for the motion of a viscous fluid:

It admits any law for viscosity.
It is generally accepted that resistance is a function of speed. Viscosity, like momentum transfer between fluid sections with different velocities, depends on the velocity gradient (but not on the velocity itself - this is prevented by the principle of relativity). If we restrict ourselves to expanding this dependence into linear terms, we get such an eerie object:

in which the value in front of the derivative contains 81 coefficients. However, using a number of completely reasonable assumptions about the homogeneity and isotropy of the fluid, from 81 coefficients you can go to only two, and in the general case for a compressible medium, the tensor of viscous stresses is equal to:

where η (this) is the shear viscosity and ζ (zeta or zeta ) Is the bulk viscosity. If the medium is also incompressible, then one shear viscosity coefficient is sufficient, since the second term leaves. This viscosity law

is called the Navier law, and the equation of motion obtained by substituting it is the Navier-Stokes equation:
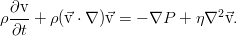
The main problem of hydrodynamics is the lack of exact solutions to its equations. No matter how they struggle with this, they still have not been able to obtain truly universal results, and I recall that the question of the existence and smoothness of solutions of the Navier-Stokes equations is on the list of the Clay Institute's Millennium Problems.
However, despite such sad facts, there are some results. Not all will be presented here, but only the simplest cases.
Of particular interest are flows in which the fluid does not swirl. For such a situation, we can refuse to consider the vector velocity field, since it is expressed through the gradient of the scalar function — the potential. The potential, on the other hand, satisfies the well-studied Laplace equation, the solution of which is completely determined by what is given at the boundaries of the region under consideration:

Moreover, in the absence of viscosity, the pressure can also be unambiguously expressed from the Euler equation, which is wonderful and leads us to a complete solution of the problem. Ah, if it had always been so ... then hydrodynamics, probably, would no longer exist as a modern and relevant industry.
In addition, it is possible to simplify the problem by assuming that the fluid flow is two-dimensional - say, everything moves in the (x, y) plane, and not a single particle moves along the z axis. It can be shown that in this case, the velocity can also be replaced by a scalar function (this time, by the stream function):

which, with a potential flow, satisfies the Cauchy-Lagrange conditions from the theory of functions of a complex variable and use the corresponding mathematical apparatus. Fully coincident with the electrostatic apparatus. The theory of potential flows is developed at a high level, and, in principle, well describes a wide range of problems.
Solutions for a viscous fluid are most often obtained when the non-linear term drops out of the Navier-Stokes equation due to the symmetry properties of the problem.
The most elementary task. A channel with a fixed lower and a movable upper wall that moves uniformly at a certain speed. At the boundaries, the fluid adheres to them, so that the fluid velocity is equal to the velocity of the boundary. This result is an experimental fact, and somehow even the authors of the first experiments are not mentioned, simply - by the totality of the experiments.
In such a situation, the Navier-Stokes equation will have an equation of the form v '' = 0, and therefore the velocity profile in the channel will be linear:

This problem is almost basic for the theory of lubrication, because allows you to directly determine the force that you want to apply to the upper wall for its movement with a specific speed.
The second most elementary is the laminar flow in the channel. Or in the pipe. The result is one - the velocity profile is parabolic:

Based on the Poiseuille solution, it is possible to determine the fluid flow through the channel section, but, however, only with a laminar flow and smooth walls. On the other hand, there are no exact solutions for turbulent flow and rough walls, but there are only approximate empirical laws.
Here - almost like in the Poiseuille problem, only the upper boundary of the liquid will be free. If we assume that no waves are running along it, and generally there is no friction from above, then the velocity profile will be almost the lower half of the previous figure. True, if we calculate the flow velocity for the average plain river from the obtained dependence, it will be about 10 km / s, and the water should spontaneously go into space. The low flow rates observed in nature are associated with the developed vorticity and turbulence of the flow, which effectively increase the viscosity of water by about 1 million times.
In the next post it is planned to talk about the law of conservation of energy and the corresponding equations of heat transfer during fluid flow.
This publication describes the basic equations of motion for an ideal and viscous fluid. If possible, their conclusion and physical meaning are briefly reviewed, and several simple examples of their exact solutions are described. Alas, these few examples of analytically available solutions of the Navier-Stokes equations are largely exhausted. Let me remind you that the Clay Institute attributed the proof of the existence and smoothness of solutions to the problems of the millennium. Geniuses of Perelman level and above - the task awaits you.
The concept of continuous medium
In, so to speak, “traditional” hydrodynamics, which has developed historically, the foundation is a model of a continuous medium. It is distracted from the molecular structure of the substance, and describes the medium by several continuous field quantities: density, velocity (determined through the total momentum of the molecules in a given volume element) and pressure. The model of a continuous medium assumes that in any infinitesimal volume there are still quite a lot of particles (as they say, there are a lot of thermodynamically - numbers that are close in order of magnitude to the Avogadro number - 10 23 pieces). Thus, the model is limited from below by the discreteness of the molecular structure of the liquid, which is completely insignificant in problems of typical spatial scales.
However, this approach allows us to describe not only water in a test tube or reservoir, and is much more universal. Since our Universe is practically homogeneous on a large scale, then, oddly enough, starting from a certain scale it is perfectly described as a continuous medium, taking into account, of course, self-gravity.
Other, more mundane applications of a continuous medium are the description of the properties of elastic bodies, plasma dynamics, bulk solids. You can also describe people’s topl as a compressible fluid.
In parallel with the approximation of a continuous medium, a kinetic model based on the discretization of the medium into small particles interacting with each other (in the simplest case, like solid balls repelling in a collision) is gaining momentum in recent years. This approach arose primarily due to the development of computer technology, however, it did not bring substantially new results into pure hydrodynamics, although it turned out to be extremely useful for problems of plasma physics, which at the micro level is not homogeneous, but contains electrons and positively charged ions. Well, again, to simulate the universe .
The equation of continuity. Mass conservation law

The most elementary law. Suppose we have some completely arbitrary, but macroscopic volume of fluid V , bounded by surface F (see. Fig.). The mass of fluid inside it is determined by the integral:

And let nothing happen to the liquid inside it, except for movement. That is, there are no chemical reactions and phase transitions, no tubes with pumps or black holes. Well, everything happens at low speeds and for small masses of matter, therefore no theory of relativity, curvature of space, self-gravity of a liquid (it becomes significant on a stellar scale). And let the volume itself and its borders are motionless. Then the only thing that can change the mass of liquid in our volume is its flow through the boundary of the volume (for definiteness, let the mass in the volume decrease):

where vector j is the flow of matter through the boundary. The point, we recall, is the scalar product. Since the boundaries of the volume, as was said, are fixed, the time derivative can be introduced under the integral. And the right-hand side can be transformed to the same as on the left, volume integral by the Gauss-Ostrogradsky theorem .
As a result, in both sides of the equality we obtain an integral over the same completely arbitrary volume, which allows us to equate the integrands and go over to the differential form of the equation:

Here (and hereinafter) the Hamilton vector operator is used. Figuratively speaking, this is a conditional vector whose components are differentiation operators with respect to the corresponding coordinates. With its help, one can very briefly denote various kinds of operations on scalars, vectors, tensors of higher ranks and other mathematical evil spirits, the main ones being gradient , divergence and rotor . I will not dwell on them in detail, since this distracts from the main topic.
Finally, the flow of matter is equal to the mass transferred through the unit area per unit time:

Finally,the mass conservation law (also called the continuity equation) for a continuous medium is as follows:

This expression is the most general for a medium with a variable density. In reality, the experiment indicates an extremely weak compressibility of the liquid and an almost constant value of the density, which allows us to apply the law of mass conservation in the form of an incompressibility condition with high accuracy:

which works with no less good accuracy for gases, while the flow velocity is low compared to the sound velocity.
Euler equation. The law of conservation of momentum
The whole relatively cumbersome process of
The reasoning is practically the same, only now we are not interested in mass, and the total momentum of the fluid in the same volume of the V . It is equal to:

Under the same conditions as above, the momentum in the volume can change due to:
- convective transfer - i.e. the impulse “flows away” along with the speed across the border
- pressure of surrounding fluid elements
- simply due to external forces, for example - from gravity.
The corresponding integrals (the order corresponds to the list) give the following relationship:

We begin to transform them. True, for this you need to use tensor analysis and rules for working with indexes. More specifically, the Gauss-Ostrogradsky theorem is applied to the first and second integrals in a generalized form (it works not only for vector fields). And if we go to the differential form of the equation, we get the following: A

cross in a circle denotes a tensor product , in this case, vectors.
In principle, this is already the Euler equation, but it can be simplified a little - after all, the law of conservation of mass has not been canceled. Having opened the brackets in the differential operators here and then citing similar terms, we will see that the three terms are safely collected inthe continuity equation , and therefore give a total of zero. The final equation turns out to be this:

If we move to a reference frame connected with a moving fluid (we will not focus on how this is done), we will see that the Euler equation expresses Newton’s second law for a unit volume of the medium.
Accounting for viscosity. The Navier-Stokes equation
An ideal fluid, of course, is good (although it still cannot be solved for sure), but in many cases viscosity accounting is necessary. Even in the same convection, during the flow of fluid through pipes. Without viscosity, water would flow out of our cranes at cosmic speeds, and the slightest temperature heterogeneity in the water would lead to its extremely rapid and rapid mixing. Therefore, let's take into account the resistance of the liquid to itself.
The Euler equation can be supplemented by various (but equivalent, of course) ways. We will use the basic technique of tensor analysis — the index form of writing the equation. And while we also discard external forces, so as not to get confused under the arms / under the legs / in front of the eyes (underline as necessary). In this situation, everything except the time derivative can be collected in the form of a divergence of one such tensor:

In meaning, this is the momentum flux density in a liquid. It is necessary to add viscous forces to it in the form of another tensor term. Since they clearly lead to a loss of energy (and momentum), they must be subtracted:

Going back to the equation with such a tensor, we get a generalized equation for the motion of a viscous fluid:

It admits any law for viscosity.
It is generally accepted that resistance is a function of speed. Viscosity, like momentum transfer between fluid sections with different velocities, depends on the velocity gradient (but not on the velocity itself - this is prevented by the principle of relativity). If we restrict ourselves to expanding this dependence into linear terms, we get such an eerie object:

in which the value in front of the derivative contains 81 coefficients. However, using a number of completely reasonable assumptions about the homogeneity and isotropy of the fluid, from 81 coefficients you can go to only two, and in the general case for a compressible medium, the tensor of viscous stresses is equal to:

where η (this) is the shear viscosity and ζ (zeta or zeta ) Is the bulk viscosity. If the medium is also incompressible, then one shear viscosity coefficient is sufficient, since the second term leaves. This viscosity law

is called the Navier law, and the equation of motion obtained by substituting it is the Navier-Stokes equation:
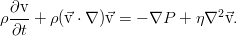
Exact Solutions
The main problem of hydrodynamics is the lack of exact solutions to its equations. No matter how they struggle with this, they still have not been able to obtain truly universal results, and I recall that the question of the existence and smoothness of solutions of the Navier-Stokes equations is on the list of the Clay Institute's Millennium Problems.
However, despite such sad facts, there are some results. Not all will be presented here, but only the simplest cases.
Potential Currents
Of particular interest are flows in which the fluid does not swirl. For such a situation, we can refuse to consider the vector velocity field, since it is expressed through the gradient of the scalar function — the potential. The potential, on the other hand, satisfies the well-studied Laplace equation, the solution of which is completely determined by what is given at the boundaries of the region under consideration:

Moreover, in the absence of viscosity, the pressure can also be unambiguously expressed from the Euler equation, which is wonderful and leads us to a complete solution of the problem. Ah, if it had always been so ... then hydrodynamics, probably, would no longer exist as a modern and relevant industry.
In addition, it is possible to simplify the problem by assuming that the fluid flow is two-dimensional - say, everything moves in the (x, y) plane, and not a single particle moves along the z axis. It can be shown that in this case, the velocity can also be replaced by a scalar function (this time, by the stream function):

which, with a potential flow, satisfies the Cauchy-Lagrange conditions from the theory of functions of a complex variable and use the corresponding mathematical apparatus. Fully coincident with the electrostatic apparatus. The theory of potential flows is developed at a high level, and, in principle, well describes a wide range of problems.
Simple viscous fluid flows
Solutions for a viscous fluid are most often obtained when the non-linear term drops out of the Navier-Stokes equation due to the symmetry properties of the problem.
Couette shear flow
The most elementary task. A channel with a fixed lower and a movable upper wall that moves uniformly at a certain speed. At the boundaries, the fluid adheres to them, so that the fluid velocity is equal to the velocity of the boundary. This result is an experimental fact, and somehow even the authors of the first experiments are not mentioned, simply - by the totality of the experiments.
In such a situation, the Navier-Stokes equation will have an equation of the form v '' = 0, and therefore the velocity profile in the channel will be linear:

This problem is almost basic for the theory of lubrication, because allows you to directly determine the force that you want to apply to the upper wall for its movement with a specific speed.
Poiseuille Current
The second most elementary is the laminar flow in the channel. Or in the pipe. The result is one - the velocity profile is parabolic:

Based on the Poiseuille solution, it is possible to determine the fluid flow through the channel section, but, however, only with a laminar flow and smooth walls. On the other hand, there are no exact solutions for turbulent flow and rough walls, but there are only approximate empirical laws.
Runoff of a fluid layer on an inclined plane
Here - almost like in the Poiseuille problem, only the upper boundary of the liquid will be free. If we assume that no waves are running along it, and generally there is no friction from above, then the velocity profile will be almost the lower half of the previous figure. True, if we calculate the flow velocity for the average plain river from the obtained dependence, it will be about 10 km / s, and the water should spontaneously go into space. The low flow rates observed in nature are associated with the developed vorticity and turbulence of the flow, which effectively increase the viscosity of water by about 1 million times.
In the next post it is planned to talk about the law of conservation of energy and the corresponding equations of heat transfer during fluid flow.
Only registered users can participate in the survey. Please come in.
Continue?
- 88.2% Yes 421
- 11.7% No 56
