November 8, 2012 at 16:32Incremental GPS Track Binding Algorithm
Geoinformation systems are gradually entering everyday life.
Most mobile devices are equipped with GPS / GLONASS receivers. This allows developers to get track records of their users (tracks). Tracks can be used to solve a number of problems - from navigating the map and informing about the location of friends to building traffic jams and predicting the traffic situation.
Unfortunately, without additional processing, the user's track is uninformative, therefore, the stage of communication of external data and the internal map of the application is required. To do this, there are special data matching algorithms (map matching algorithms).
This article is devoted to the algorithm for linking a track to a road graph and the results of its application in the
The algorithm that will be discussed, processes the incoming track, receiving at the output a sequence of edges of the road graph, which repeat the input data as closely as possible with their geometry.
A road graph is one of the foundations of a geographic information application. It contains inside itself all the information about the roads: from the type of coating and the number of lanes to their geometry. There are several ways to represent a road graph in computer memory.
Consider the simplest option: a directional graph in which nodes are intersections, and edges are roads. This simplification makes it difficult to verify traffic rules, but facilitates further calculations. Roads with traffic in both directions in a similar column will be represented by a pair of edges. An edge is an indivisible unit of the path. However, an edge is a mathematical representation of a road. The actual location of the road on the map (a set of road coordinate points) will be determined by a separate property of this edge of the graph, which we will call the geometry of the road.
A track is an ordered sequence of points containing some error. Due to this error, the point will almost never lie on the edge of the graph to which it is necessary to attach. According to the meanness law for GPS data, the positioning error is less in a clean field than in the city center. In other words, the point arriving can hit a neighboring edge.
This is how one Moscow interchange looks with the eyes of the maps:
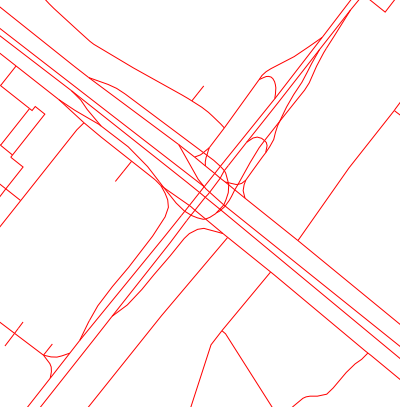
And so, according to the version of navigators, our users go on it:
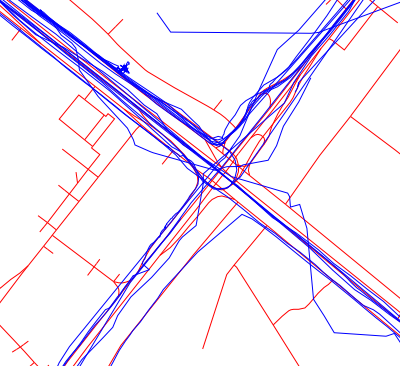
Track Binding Process
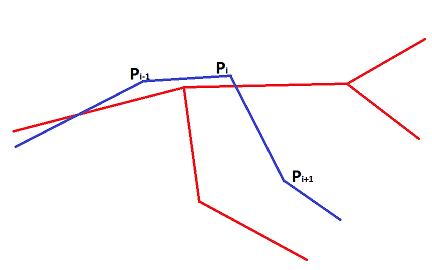
To snap a point on a track to a graph in the simplest case, you need to find edges with a minimum distance from edge to point. Unfortunately, in practice (especially in the city center), a route tied in this way can turn out to be a set of ribs not connected to each other. In order to improve the quality of the binding, we assume that the track is an ordered targeted movement of the user along the geometries of the edges of the graph. That is, the entire route passes along ribs connected with each other. At the same time, for each edge of the route, there may be several points on the track, and not a single one.
Thus, since we refuse to take the edge closest to the point, we need to choose some other quantitative measure that would allow us to determine how much the measured edge is suitable for snapping.
There are many factors that can be used in this case:
- The distance from the point to the geometry of the edge of the graph. Estimates both the shortest distance and the likelihood that the receiver could make such a mistake.
- The coincidence of the directions of motion. Estimates the angle between the vehicle’s motion vector and the direction of the edge geometry to which the point is bound. (This measure is resistant to the systematic error of the GPS receiver, but subject to random).
- Changing the direction of the vehicle. The likelihood that the car will turn off the main road is generally less than the likelihood that it will continue to move along it (this minimizes the number of maneuvers).
- The physical ability to transition from one rib to another (reach of the rib). The adequacy of the speed at which the car had to move in order to make this transition.
Based on these factors, a likelihood assessment formula is created. The Frechet distance is used as one of these formulas . Simply put, this is the minimum required length of a dog leash if the owner follows the road graph and his pet follows the GPS track. This estimate focuses only on the geographical remoteness of the track being laid.
To bind tracks in this article, we use the estimation formula for an incremental data-binding algorithm (based on the work of S. Barcatsoulas [2]).
This formula includes two main components:
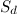and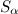 
. The component
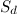takes into account the weighted distance from the track point to the edge and is calculated by the formula:, 
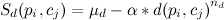where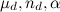 
are the scaling factors, and
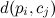Is the distance from the point p i to the geometry of the edge c j . The component
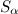takes into account the angle between the direction of the geometry of the edge and the direction of the track: 
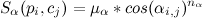where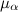 
and 
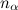are the scaling factors, and cos (α i, j ) is the angle between the geometry of the ith edge of the graph and the direction of movement along the edge of the track 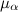and 
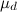are the parameters that affect the importance of the components. For the algorithm, the values of these parameters relative to each other are important - this determines which of the factors will have more weight when comparing. The parameters
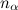and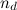 
affect the sensitivity to a change in the described factor. After calculating the components, the final metric is calculated as:
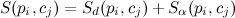
The larger the result, the better the coincidence of the track section and the edge.
Having the likelihood formula of the route being plotted in the arsenal, you can describe the binding algorithm:
Выбрать все рёбра графа с геометрией, пересекающей дельта окрестность первой точки трека;Оценить все выбранные рёбра с помощью формулы;Выбрать ребро с наибольшей оценкой. Сделать его текущим и добавить его к готовому маршруту;Если ближайшая к точке трека точка на геометрии ребра находится не на конце ребра, то выбрать следующую точку трека. (Если больше точек нет, то привязка закончена);Выбрать все исходящие из текущего рёбра графа и текущее ребро;Перейти к 2;
Follow-up Strategy
The undoubted advantage of the chosen formula is the ability to assess the likelihood of a binding to the graph not only for one point, but also for the route as a whole. This can be used to implement a strategy for accounting for subsequent points. If not the last point of the route is currently attached, then you can calculate the estimates of the following points, provided that the route runs along the selected edge. After that, you can compare the sum of the likelihood estimates. This will avoid errors at complex junctions and intersections, as the algorithm will select the edges taking into account the subsequent movement.
A little bit about performance
The task of linking one track is not incredibly expensive, but in practice, rarely does anyone ever tie a pair of tracks. As a rule, you need to manage to tie thousands of points per second. Therefore, you have to find a compromise between processing speed and track binding accuracy. In the chosen algorithm, the number of estimated edges for each track point and the depth of point estimation “from the future” affect the performance. As practice has shown, in order to make the right decision about behavior at intersections, in most cases it is enough to take into account 2-3 subsequent points of the track.
The number of estimated edges in fact is difficult to change, because for a high-quality binding, after selecting the first edge, it is necessary to evaluate all outgoing edges. But one may not consider options with too low a likelihood score.
Summary
The implementation of the binding algorithm allowed the
Related Literature
- “Map Matching. An Introduction ”Prof. David Bernstein, James Madison University.
- “On Map-Matching Vehicle tracking Data” Sotiris Bracatsoulas, Dieter Pfoser Randall Salas Carola Wank VLDB'05
- “Approximate Map Matching with respect to the Frechet Distance” Daniel Chen, Anne Driemel, Leonidas J. Guibas, Andy Nguyen, Carola Wenk. Stanford 2011
Lev Dragunov, a programmer for Maps Rambler's Top100