Hello! My name is Misha Kamenshchikov, I am engaged in Data Science and the development of microservices in the Avito recommendation team. In this article I will tell you about our recommendations of similar ads and how we improve them with the help of multi-armed bandits. I spoke on this topic at the Highload ++ Siberia conference and at the Data & Science: Marketing event .

Article layout

• Recommendations on Avito
• Similar service
• Rankers and configs
• A / B tests and multi-armed bandits
• Selection of target actions
• results

Recommendations on Avito

First, a small overview of all types of recommendations that are on Avito.

Personalized User-Item Recommendations

User-Item recommendations are based on user actions and are designed to help him quickly find the product of interest, or show something potentially interesting. They can be seen on the home page of the site and applications or in mailing lists. To create such recommendations, we use two types of models: offline and online.
The offline models are based on matrix factorization algorithms, which are trained on all data for several days, and recommendations are added to a fast repository for distribution to users. Online models consider recommendations on the fly, using the content of ads from the user's history. The advantage of offline models is that they give more accurate and high-quality recommendations, but at the same time they do not take into account the most recent actions of users that could occur during the training of the model when the training set was recorded. Online models immediately respond to user actions, and recommendations can change with every action.

Cold-start recommendations

All recommender systems have a so-called “cold start” problem. Its meaning is that the models described above cannot give recommendations to a new user without a history of actions. In such cases, it is better to acquaint the user with what is on the site, while choosing not just random ads, but, for example, ads from categories that are popular in the user's region.

Search recommendations

For users who often use the search, we make the recommended shortcuts for the search - they send the user to a specific category and set filters. Such recommendations can be found at the top of the main page of the application.

Item Item Recommendations

Item-Item recommendations are presented on the site in the form of similar ads on the item card. They can be seen on all platforms under the ad description. The model of recommendations at the moment is exclusively content and does not use information about the actions of users, therefore, to the new ad we can immediately pick up similar ones among the active ads on the site. Further in the article I will talk about this type of recommendations.

In more detail about all kinds of recommendations on Avito, we have already written in our blog. Read if you are interested.

Similar listings

Here is the block with similar ads:

This type of recommendation appeared on the site before anything else, and the logic was implemented on the search engine Sphinx . In fact, this model is a linear combination of various factors: word coincidence, distance, price difference, and other parameters.

Based on the parameters of the target ad, a query is generated in Sphinx, and embedded rankers are used for ranking.

Request example:

SELECTid,
    weight as ranker_weight,
    ranker_weight * 10 +
    (metro_id=42) * 5 +
    (location_id=2525) * 10 +
    (110000 / (abs(price - 1100000) + 110000)) * 5as rel
FROM items
WHEREMATCH('@title велосипед|scott|scale|700|premium') AND microcat_id=100ORDERBY rel DESC, sort_time DESCLIMIT0,32OPTION max_matches=32,
ranker=expr('sum(word_count)')

If we try to describe this approach more formally, then we can represent rankers in the form of some weights. $$and ad parameters $$ (source - source ad) and $$(target ad). For each of the parameters, we introduce the similarity function$$. They can be binary (for example, the coincidence of the city of ads), can be discrete (the distance between ads) and continuous (for example, the relative difference in price). Then for two ads the final score will be expressed by the formula

$$

Using the search engine, you can quickly read the value of this formula for a sufficiently large number of ads and rank the issue in real time.

This approach did very well in its original form, but it had significant drawbacks.

Approach problems

First, the weights were originally chosen expertly and were not subject to doubt. Sometimes there were changes in the scales, but they were made on the basis of a point feedback, and not on the basis of analyzing the behavior of users in general.

Secondly, the weights were hardened in the site, and it was very inconvenient to make changes to them.

A step towards automation

The first step towards improving the model of recommendations was the removal of all logic into a separate microservice in Python. This service was fully owned by our recommendation team, and we were able to conduct experiments quite often.
Each experiment can be characterized by the so-called "config" - a set of weights for rankers. We want to generate configs and choose the best one based on user actions. How can I generate these configs?

The first option, which was from the very beginning, is the expert generation of configs. That is, using knowledge from the subject area, we assume that, for example, when searching for a car, people are interested in options that are close in price to the one being viewed, and not just similar models that can cost significantly more.

The second option is random configs. We set some distribution for each of the parameters and then just take a sample from this distribution. This method is faster, because you do not need to think about each of the parameters for all categories.

A more complicated option is to use genetic algorithms. We know which configs give us the best effect in terms of user actions, so at each iteration we can leave them and add new ones: random or expert.

An even more complicated option that requires a fairly long history of experiments is the use of machine learning. We can present a set of parameters as a feature vector, and a target metric as a target variable. Then we will find a set of parameters that the model estimates will maximize our target metric.
In our case, we stopped at the first two approaches, as well as genetic algorithms in the simplest form: leave the best, remove the worst.

Now we’ve gotten to the most interesting part of the article: we can generate configs, but how to conduct experiments so that it is fast and efficient?

Conducting experiments

The experiment can be carried out in the A / B / ... test format. To do this, we need to generate N configs, wait for statistically significant results and, finally, choose the best config. This may take quite a long time, and throughout the test a fixed group of users may receive recommendations of poor quality - with the random generation of configs, this is quite possible. Also, if we want to add some new config to the experiment, we will have to restart the test again. But we want to conduct experiments quickly, to be able to change the conditions of the experiment. And so that users do not suffer from obviously bad configs. This will help us multi-armed bandits.

Multi-armed bandits

The names of the method came from the "one-armed gangsters" - slot machines in a casino with a lever for which you can pull and get a win. Imagine that you are in the hall with a dozen of such machines, and you have N free attempts to play any of them. You, of course, want to win more money, but do not know in advance which machine gives the biggest win. The problem of multi-armed bandits is precisely to find the most profitable machine gun with minimal losses (playing unprofitable machine guns).

If we formulate it in terms of our recommendations, it turns out that automata are configs, each attempt is a choice of a config for generating recommendations, and a win is a certain target metric depending on the feedback of users.

The advantage of gangsters over A / B / ... tests

Their main advantage is that they allow us to change the amount of traffic depending on the success of a particular config. This solves the problem that people will receive bad recommendations throughout the experiment. If they do not click on the recommendations, the gangster will understand this quickly enough and will not choose this config. In addition, we can always add a new config to the experiment or simply remove one of the current ones. All this gives us flexibility in conducting experiments and solves the problems of the approach with A / B / ... testing.

Gangster strategies

There are a lot of strategies for solving the problem of multi-armed bandits. Next, I will describe several classes of simple-to-implement strategies that we tried to apply in our task. But first you need to understand how to compare the effectiveness of strategies. If we know in advance which pen gives the maximum gain, then the optimal strategy is to always pull this pen. Fix the number of steps and calculate the optimal reward.$$. For the strategy also calculate the award$$ and we introduce the concept $$:

$$

Further strategies can be compared just this value. I note that strategies have character changes$$ may be different, and one strategy may be better for a small number of steps, and another for a large one.

Greedy strategies

As the name suggests, greedy strategies are based on one simple principle - we always choose the pen that, on average, gives the greatest reward. The strategies of this class differ in how we explore the environment in order to determine this very pen. There are for example$$strategy. She has a single parameter -$$that determines the probability with which we choose not the best pen, but a random one, thus exploring our environment. You can also reduce the likelihood of research with time. This strategy is called$$. Greedy strategies are very simple to implement and understandable, but not always effective.

UCB1

This strategy is fully deterministic - the handle is uniquely determined from the information currently available. Here is the formula:

$$

Part of the formula with $$means the average j-th pen and is responsible for exploitation, just like in greedy strategies. The second part of the formula is responsible for the exploration,$$ - this is the total number of actions $$- the number of actions of the j-th pen. There is a proven score for this strategy.$$. You can read about it here .

Sampling Thompson

In this strategy, we assign a random distribution to each pen, and at each step we sample from this distribution the numbers, choosing the pen according to the maximum. On the basis of feedback, we update the distribution parameters so that the best handles correspond to the distribution with a large average, and its dispersion decreases with the number of actions. You can read more about this strategy in an excellent article .

Comparison of strategies

Let's carry out a simulation of the strategies described above on an artificial environment with three handles, each of which corresponds to a Bernoulli distribution with the parameter $$respectively. Our strategies:

• $$ with $$;
• UCB1;
• beta-thompson sampling.

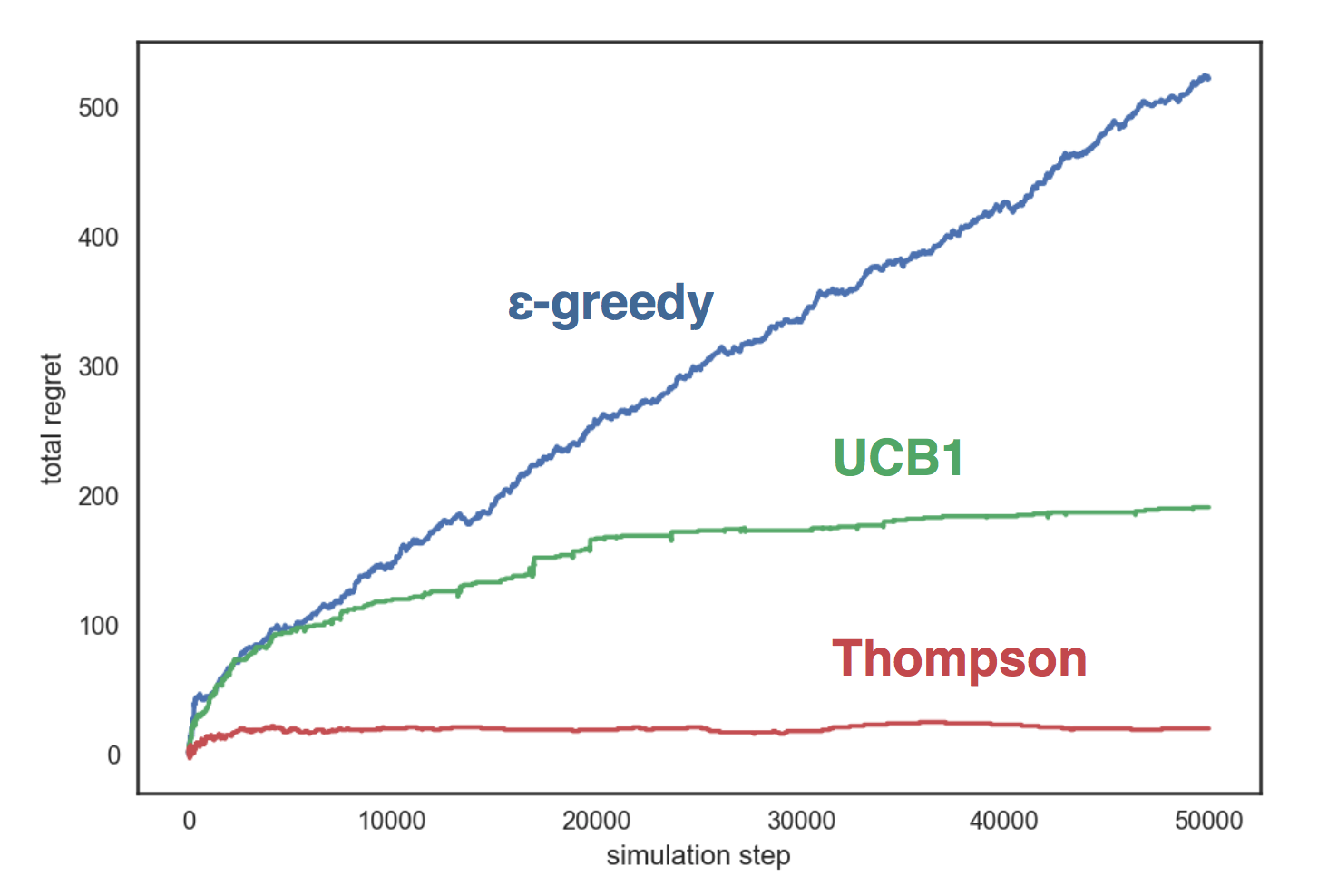
The graph shows that the greedy strategy $$ grows linearly, and the other two strategies - logarithmically, and Thompson’s sampling is much better than others and its $$almost does not grow with the number of steps.
Comparison code is posted on GitHub .

I introduced you to multi-armed bandits and now I can tell you how we used them.

Multi-armed bandits in Avito

So, we have several configs (parameter sets), and we want to choose the best of them with the help of multi-armed bandits. In order for gangsters to learn, we need one important detail - a user feedback. At the same time, the choice of actions for which we are trained should be consistent with our goals - I want users to make more deals with the help of better recommendations.

Select target actions

The first approach to the selection of targeted actions was fairly simple and naive. We chose the number of views as the target metric, and the gangsters learned well how to optimize this metric. But a problem arose: more views are not always good. For example, in the “Auto” category we managed to increase the number of views by 15%, but the number of contact requests on the contrary fell by about the same amount. On closer inspection, it turned out that the gangsters were choosing a pen in which the filter was turned off by region. Therefore, the block showed ads from all over Russia, where the choice of similar ads, of course, more. This caused an increase in the number of views: externally, the recommendations seemed to be of higher quality, but when entering the product card, people understood that the car was very far from them, and did not make a contact request.

The second approach is to learn how to convert from viewing a block to a contact request. This approach seemed better than the previous one, if only because this metric is almost directly responsible for the quality of the recommendations. But there was another problem - daily seasonality. Depending on the time of day, the conversion values ​​may differ by four (!) Times (this is often more than the effect of a better config), and the handle, which was lucky to be selected in the first interval with a high conversion, continued to be chosen more often than others.

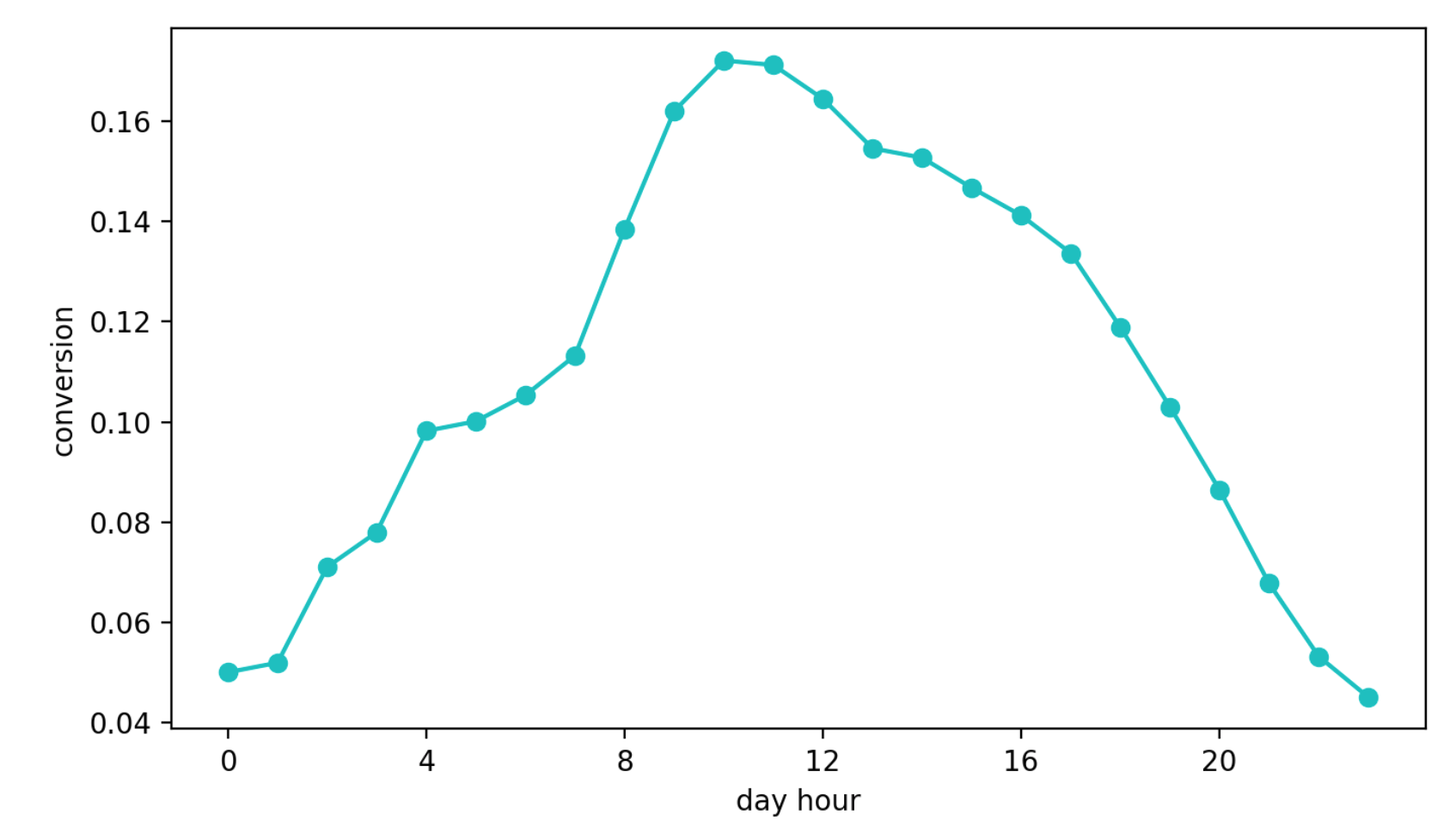
_{Daily dynamics of conversion (values ​​along the Y axis are changed)}

Finally, the third approach. We use it now. We select the reference group, which always receives recommendations on the same algorithm and is not subject to the influence of bandits. Next, we look at the absolute number of contacts in our target group and reference. Their attitude is not subject to seasonality, since we isolate the reference group by chance, and this approach conveniently falls on the Thompson sampling.

Our strategy

Select the reference and target groups, as described above. Then we initialize N handles (each corresponds to a config) with a beta distribution.$$

At each step:

• for each pen, we sample the number from the corresponding distribution and select the pen according to the maximum;
• count the number of actions in groups $$ and $$ for a certain time quantum (in our case it is 10 seconds) and update the distribution parameters for the selected handle: $$, $$.

When using this strategy, we optimize the metric we need, the number of contact requests in the target group and avoid the problems I described above. In addition, in the global A / B test, this approach showed the best results.

results

The global A / B test was organized as follows: all ads are randomly divided into two groups. We show the recommendations of one of them with the help of bandits, and the other with the old expert algorithm. Then we measure the number of contact conversion requests in each group (requests made after switching to ads from a similar block). On average, in all categories the group with bandits gets about 10% more targeted actions than the control group, but in some categories this difference can reach as much as 30%.

And the platform created allows you to quickly change the logic, adding configs to gangsters, and validate hypotheses.

If you have questions about our recommendation service or about multi-armed gangsters, ask them in the comments. I am happy to answer.