Capsular Neural Networks

In 2017, Jeffrey Hinton (one of the founders of the error back propagation approach) published an article describing capsular neural networks and proposing an algorithm for dynamic routing between capsules to teach the proposed architecture.

Classic convolutional neural networks have disadvantages. The internal representation of convolutional neural network data does not take into account spatial hierarchies between simple and complex objects. So, if the eyes, nose and lips for a convolutional neural network are randomly displayed in the image, this is a clear sign of the presence of a face. And the rotation of the object affects the quality of recognition, while the human brain easily solves this problem.


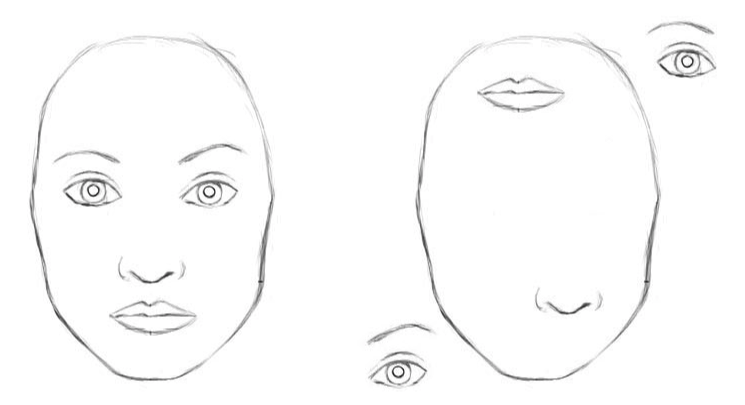
For a convolutional neural network, 2 images are similar [2]


Thousands of examples will be needed to train object recognition from various CNN angles.


Capsule networks reduce the recognition error of an object from another angle by 45%.

Prescription capsules

Capsules encapsulate information about the state of the function, which is found in vector form. Capsules encode the probability of detecting an object as the length of the output vector. The state of the detected function is encoded as the direction in which the vector points (“instance creation parameters”). Therefore, when the detected function moves through the image or the state of the image changes, the probability remains unchanged (the length of the vector does not change), but the orientation changes.

Imagine that a capsule detects a face in an image and outputs a 3D vector of length 0.99. Then, move the face in the image. The vector will rotate in its space, representing a changing state, but its length will remain fixed because the capsule is confident that it has detected a face.



Differences between capsules and neurons. [2]

An artificial neuron can be described in three steps:

1. scalar weighting of input scalars
2. sum of weighted input scalars
3. non-linear scalar transformation.

The capsule has the vector forms of the above 3 steps, in addition to the new stage of the affine transformation of input:

1. matrix multiplication of input vectors
2. scalar weighting of input vectors
3. sum of weighted input vectors
4. vector nonlinearity.

Another innovation introduced in CapsNet is a new nonlinear activation function that takes a vector and then “gives out” its length no more than 1, but does not change direction.



The right side of the equation (blue rectangle) scales the input vector so that the vector has a block length, and the left side (red rectangle) performs additional scaling.

The capsule design is based on the construction of an artificial neuron, but extends it to a vector form to provide more powerful representative capabilities. Matrix weights are also introduced for coding hierarchical relationships between features of different layers. The equivariance of neural activity is achieved in relation to changes in input data and invariance in the probabilities of detecting signs.

Dynamic routing between capsules

The dynamic routing algorithm [1].

The first line says that this procedure takes capsules at the lower level l and their outputs u_hat, as well as the number of routing iterations r. The last line says that the algorithm will produce the output of a higher level capsule v_j.

The second line contains a new coefficient b_ij, which we have not seen before. This coefficient is a temporary value that will be iteratively updated, and after the procedure is completed, its value will be stored in c_ij. At the beginning of training, the value of b_ij is initialized to zero.

Line 3 says steps 4-7 will be repeated r times.
The step in line 4 calculates the value of the vector c_i, which is all the routing weights for the lower capsule i.

After the weights c_ij are calculated for the capsules of the lower level, go to line 5, where we look at the capsules of a higher level. This step computes a linear combination of input vectors weighted using the routing coefficients c_ij defined in the previous step.

Then, in line 6, the vectors of the last step pass through a nonlinear transformation, which guarantees the direction of the vector, but its length should not exceed 1. This step creates the output vector v_j for all higher levels of the capsule. [2]
The basic idea is that the similarity between input and output is measured as the scalar product between the input and output of the capsule, and then the routing coefficient changes. Best practice is to use three routing iterations.

Conclusion

Capsular neural networks are a promising architecture of neural networks that improves image recognition with changing angles and hierarchical structure. Capsular neural networks are trained using dynamic routing between capsules. Capsule networks reduce the recognition error of an object from a different angle by 45% compared to CNN.