If in one of my previous posts it was a fairly modern approach to building balanced search trees, then this post is devoted to the implementation of AVL trees - probably the very first type of balanced binary search trees invented back in 1962 by our (then Soviet) scientists Adelson -Welsky and Landis. You can find many realizations of AVL trees on the network (for example, here ), but everything that I personally saw does not inspire much optimism, especially if you are trying to figure everything out from scratch. Everywhere it is argued that AVL trees are simpler than red-black trees , but looking at the code attached to this, you begin to doubt this statement. Actually, the desire to explain on fingers how the AVL trees are arranged was the motivation for writing this post. The presentation is illustrated by C ++ code.

The concept of AVL tree

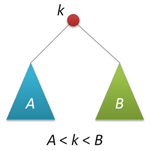An AVL tree is primarily a binary search tree, the keys of which satisfy the standard property: the key of any tree node is not less than any key in the left subtree of this node and not more than any key in the right subtree of this node. This means that you can use the standard algorithm to search for the desired key in the AVL tree. For simplicity, we will assume that all keys in the tree are integer and not repeated.

A feature of the AVL tree is that it is balanced in the following sense: for any tree node, the height of its right subtree differs from the height of the left subtree by no more than one. It is proved that this property is sufficient for the height of the tree to logarithmically depend on the number of its nodes: the height h of the AVL tree with n keys lies in the range from log ₂ (n + 1) to 1.44 log ₂ (n + 2) - 0.328. And since the basic operations on binary search trees (search, insertion and deletion of nodes) linearly depend on its height, we obtain a guaranteed logarithmic dependence of the operating time of these algorithms on the number of keys stored in the tree. Recall that randomized search trees provide balance only in the probabilistic sense: the probability of obtaining a highly unbalanced tree for large n, although it is negligible, remains non-zero .

Node structure

We will represent the nodes of the AVL tree with the following structure:

struct node // структура для представления узлов дерева
{
	int key;
	unsigned char height;
	node* left;
	node* right;
	node(int k) { key = k; left = right = 0; height = 1; }
};

The key field stores the node key, the height field is the height of the subtree with the root in the given node, the left and right fields are pointers to the left and right subtrees. A simple constructor creates a new node (height 1) with the given key k.

Traditionally, the nodes of the AVL tree do not store the height, but the difference in the heights of the right and left subtrees (the so-called balance factor), which can take only three values ​​-1, 0 and 1. However, note that this difference is still stored in a variable, the size of which is equal to at least one byte (unless you come up with some tricky schemes of "effective" packaging of such quantities). Recall that the height h <1.44 log ₂ (n + 2), which means, for example, that for n = 10 ⁹(one billion keys, more than 10 gigabytes of memory for storing nodes) the height of the tree will not exceed h = 44, which successfully fits in the same one byte of memory as the balance factor. Thus, storing heights on the one hand does not increase the amount of memory allocated to tree nodes, but on the other hand greatly simplifies the implementation of some operations.

We define three auxiliary functions related to height. The first is a wrapper for the height field, it can work with null pointers (with empty trees):

unsigned char height(node* p)
{
	return p?p->height:0;
}

The second calculates the balance factor of the given node (and only works with non-zero pointers):

int bfactor(node* p)
{
	return height(p->right)-height(p->left);
}

The third function restores the correct value of the height field of the given node (provided that the values ​​of this field in the right and left child nodes are correct):

void fixheight(node* p)
{
	unsigned char hl = height(p->left);
	unsigned char hr = height(p->right);
	p->height = (hl>hr?hl:hr)+1;
}

Note that all three functions are non-recursive, i.e. their operating time is the value of O (1).

Node balancing

In the process of adding or removing nodes in the AVL tree, a situation may arise when the balance factor of some nodes turns out to be 2 or -2, i.e. there is an imbalance of the subtree. To rectify the situation, well-known twists and turns around certain tree nodes are used. Let me remind you that a simple turn to the right (left) produces the following tree transformation:



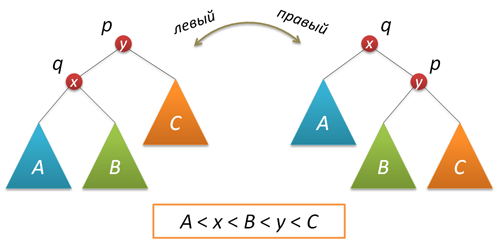
The code that implements the right turn looks like this (as usual, each function that changes the tree returns a new root of the resulting tree):

node* rotateright(node* p) // правый поворот вокруг p
{
	node* q = p->left;
	p->left = q->right;
	q->right = p;
	fixheight(p);
	fixheight(q);
	return q;
}

The left turn is a symmetrical copy of the right:

node* rotateleft(node* q) // левый поворот вокруг q
{
	node* p = q->right;
	q->right = p->left;
	p->left = q;
	fixheight(q);
	fixheight(p);
	return p;
}

Let us now consider the situation of imbalance when the height of the right subtree of node p is 2 greater than the height of the left subtree (the opposite case is symmetric and is implemented similarly). Let q be the right child node of p and s the left child node of q.



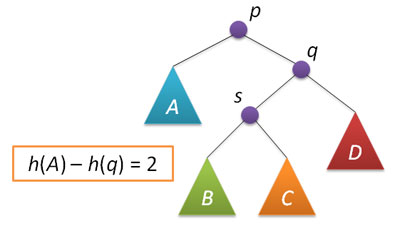
An analysis of possible cases within the framework of this situation shows that to correct the imbalance in the node p, it is sufficient to either perform a simple left turn around p or a so-called large left turn around the same p. A simple rotation is performed provided that the height of the left subtree of the node q is greater than the height of its right subtree: h (s) ≤h (D).



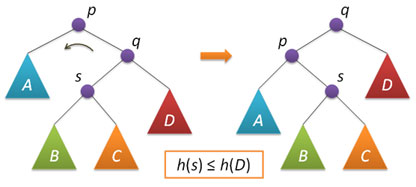
A large rotation is applied under the condition h (s)> h (D) and in this case is reduced to two simple ones - first, a right rotation around q and then a left rotation around p.



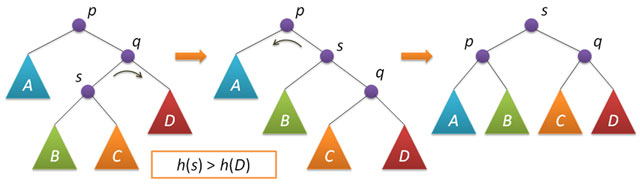
The code that performs balancing comes down to checking conditions and performing turns:

node* balance(node* p) // балансировка узла p
{
	fixheight(p);
	if( bfactor(p)==2 )
	{
		if( bfactor(p->right) < 0 )
			p->right = rotateright(p->right);
		return rotateleft(p);
	}
	if( bfactor(p)==-2 )
	{
		if( bfactor(p->left) > 0  )
			p->left = rotateleft(p->left);
		return rotateright(p);
	}
	return p; // балансировка не нужна
}

The described functions of rotations and balancing also contain neither cycles nor recursion, which means that they are performed for a constant time, independent of the size of the AVL tree.

Key insertion

The new key is inserted into the AVL tree, by and large, in the same way as in simple search trees: we go down the tree, choosing the right or left direction of movement, depending on the result of comparing the key in the current node and the key to be inserted. The only difference is that when you return from recursion (i.e., after the key is inserted into either the right or left subtree, and this tree is balanced), the current node is balanced. It is strictly proved that the imbalance arising from such an insertion at any node along the path does not exceed two, which means that the application of the balancing function described above is correct.

node* insert(node* p, int k) // вставка ключа k в дерево с корнем p
{
	if( !p ) return new node(k);
	if( kkey )
		p->left = insert(p->left,k);
	else
		p->right = insert(p->right,k);
	return balance(p);
}

In order to verify the conformity of the implemented insert algorithm with theoretical estimates for the height of the AVL trees, a simple computational experiment was conducted. An array was generated from randomly located numbers from 1 to 10,000, then these numbers were sequentially inserted into the initially empty AVL tree and the height of the tree was measured after each insertion. The results were averaged over 1000 calculations. The following graph shows the dependence on n of average height (red line); minimum height (green line); maximum height (blue line). In addition, upper and lower theoretical estimates are shown.



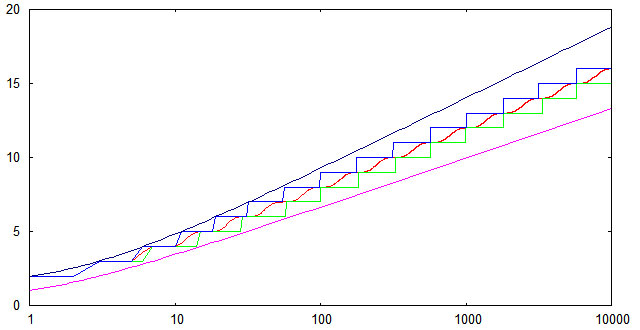
It can be seen that for random sequences of keys, experimentally found heights fall into theoretical boundaries even with a small margin. A lower bound is achievable (at least at some points) if the original key sequence is ordered in ascending order.

Key Removal

With the removal of nodes from the AVL tree, unfortunately, everything is not as chocolate as with the randomized search trees. A method based on the merger (join) of two trees, neither found nor come up with. 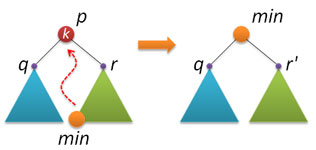Therefore, the basis was taken of the option described almost everywhere (and which is usually used when deleting nodes from the standard binary search tree). The idea is this: we find the node p with the given key k (if we don’t find it, then we don’t need to do anything), in the right subtree we find the min node with the smallest key and replace the deleted node p with the found min node.

When implementing, there are several nuances. First of all, if the found node p does not have a right subtree, then by the property of the AVL tree on the left, this node can have only one single child node (tree of height 1), or the node p in general is a leaf. In both of these cases, you just need to remove the node p and return the pointer to the left child node of the node p as the result.

Now let p have a right subtree. We find the minimum key in this subtree. By the property of the binary search tree, this key is located at the end of the left branch, starting from the root of the tree. We use a recursive function:

node* findmin(node* p) // поиск узла с минимальным ключом в дереве p 
{
	return p->left?findmin(p->left):p;
}

Another utility function will be to remove the minimum element from a given tree. Again, by the property of the AVL tree, the minimum element on the right either has a single node suspended or is empty there. In both cases, you just need to return the pointer to the right node and perform balancing on the way back (when returning from recursion). The minimal node itself is not deleted, because he is still useful to us.

node* removemin(node* p) // удаление узла с минимальным ключом из дерева p
{
	if( p->left==0 )
		return p->right;
	p->left = removemin(p->left);
	return balance(p);
}

Now everything is ready to implement the removal of the key from the AVL tree. First, we find the desired node by performing the same actions as when inserting the key:

node* remove(node* p, int k) // удаление ключа k из дерева p
{
	if( !p ) return 0;
	if( k < p->key )
		p->left = remove(p->left,k);
	else if( k > p->key )
		p->right = remove(p->right,k);	

Once the key k is found, go to plan B: remember the roots q and r of the left and right subtrees of the node p; delete the node p; if the right subtree is empty, then return the pointer to the left subtree; if the right subtree is not empty, then we find the minimum element min there, then we extract it from there, hang q from the left to min, and what turned out from r to the right, return min after balancing it.

	else //  k == p->key 
	{
		node* q = p->left;
		node* r = p->right;
		delete p;
		if( !r ) return q;
		node* min = findmin(r);
		min->right = removemin(r);
		min->left = q;
		return balance(min);
	}

When you exit recursion, do not forget to balance:

	return balance(p);
}

That's all! The search for the minimum node and its extraction, in principle, can be implemented in one function, and you will have to solve the (not very difficult) problem of returning a pair of pointers from the function. But you can save on one pass on the right subtree.

Obviously, the insert and delete operations (as well as the simpler search operation) are performed in a time proportional to the height of the tree, because in the process of performing these operations, a descent from the root to a given node is performed, and at each level, a fixed number of actions are performed. And due to the fact that the AVL tree is balanced, its height depends logarithmically on the number of nodes. Thus, the execution time of all three basic operations is guaranteed to depend logarithmically on the number of tree nodes.

Thank you all for your attention!

Sources

• B. Pfaff, An Introduction to Binary Search Trees and Balanced Trees - libavl library description
• N. Wirth, Algorithms and data structures - balanced trees according to Virt - these are just AVL trees
• T. Kormen et al., Algorithms: construction and analysis - ABL trees are described in exercises to the chapter on red-black trees
• D. Knut, The Art of Programming - Section 6.2.3 is devoted to the theoretical analysis of AVL trees.