MIT course "Security of computer systems". Lecture 2: "Control of hacker attacks", part 3

Massachusetts Institute of Technology. Lecture course # 6.858. "Security of computer systems." Nikolai Zeldovich, James Mykens. year 2014

Computer Systems Security is a course on the development and implementation of secure computer systems. Lectures cover threat models, attacks that compromise security, and security methods based on the latest scientific work. Topics include operating system (OS) security, capabilities, information flow control, language security, network protocols, hardware protection and security in web applications.

Lecture 1: "Introduction: threat models" Part 1 / Part 2 / Part 3
Lecture 2: "Control of hacker attacks" Part 1 / Part 2 / Part 3

Can you say what the disadvantage of the security approach is when using the guard page ?

Audience: it takes longer!

Professor: exactly like that! So imagine that this bunch is very, very small, but I selected a whole page to make sure that this tiny little thing did not come under attack on the pointer. This is a very spatial-intensive process, and people do not actually deploy something similar in a working environment. This can be useful for testing "bugs", but you would never do that for a real program. I think now you understand what the electric fence memory debugger is .

Audience: why size pages guard pagemust be so big?

Professor: The reason is that when determining page sizes, they usually rely on hardware, such as page-level security. For most computers, for each dedicated buffer, 2 pages of 4 KB are allocated, for a total of 8 KB. Since the heap consists of objects, for each malloc function its own page is allocated. In some modes, this debugger does not return the reserved space to the program, so the Electric fence is very voracious in terms of memory and should not be compiled with a working code.



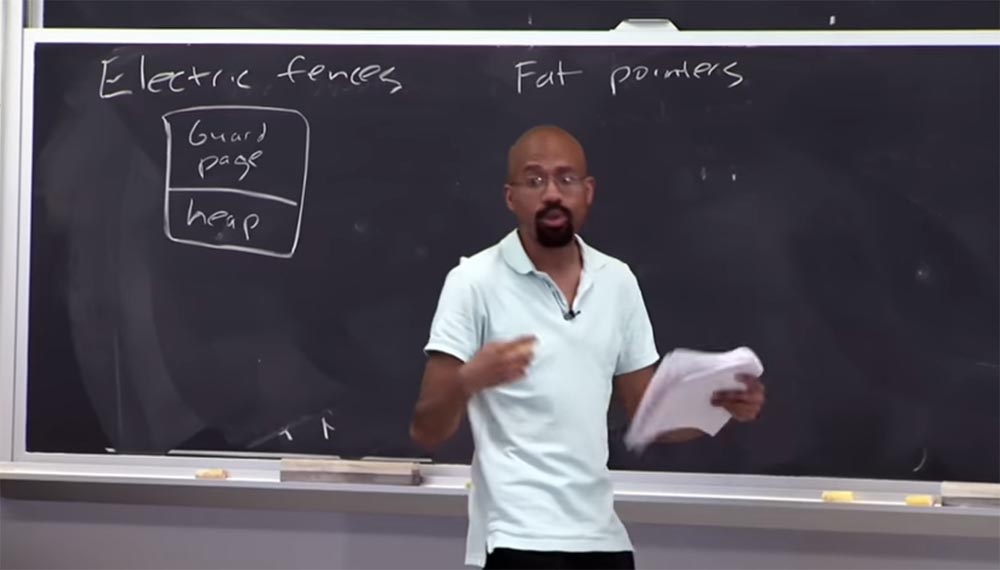
Another approach to security that is worth a look is called Fat pointers, or "fat pointers." In this case, the term “thick” means that a large amount of data is attached to the pointer. In this case, the idea is that we want to change the very representation of the pointer to include information about the boundaries.

A regular 32-bit pointer consists of 32 bits, and addresses are located inside it. If we consider the “thick pointer”, then it consists of 3 parts. The first part is the base of 4 bytes, to which the ending is also attached of 4 bytes. In the first part, the object begins, in the second it ends, and in the third, also 4-byte, the address is cur . And within these common boundaries is a pointer.



Thus, when the compiler generates an access code for this “thick pointer”, it updates the contents of the last part.cur address and simultaneously checks the contents of the first two parts to make sure that nothing bad happened to the pointer during the update process.

Imagine that I have this code: int * ptr = malloc (8) , this is a pointer for which 8 bytes are allocated. Next, I have some while loop , which is just going to assign a value to a pointer, and then an increase in the ptr ++ pointer follows . Each time this code is executed on the current address of the cur address pointer , it checks whether the pointer is within the limits specified in the first and second parts.

This happens in the new code that the compiler generates. In an online group, the question often arises of what “instrumental code” is. This is the code that the compiler generates. As a programmer, you see only what is depicted on the right — these 4 lines. But before this operation, the compiler inserts a new C code into cur address , assigns a value to the pointer, and each time checks the boundaries.



And if, when using a new code, a value exceeds the limits, the function is interrupted. This is what is called an “instrumental code.” This means that you take the source code using a C program, then add a new C source code, and then compile a new program. So the basic idea behind Fat pointers is pretty simple.

There are some drawbacks to this approach. The biggest disadvantage is the large pointer size. And this means that you can not just take the "thick pointer" and pass it in unchanged form, outside the shell library. Because there may be an expectation that the pointer has a standard size, and the program will give it this size, which it will not fit into, which will cause everything to explode. There are also problems if you want to include pointers of this type in a struct or something like it, because they can resize a struct .

Therefore, a very popular thing in C code is to take something the size of a struct.and then do something based on this size — reserve disk space for structures of this size, and so on.

And another delicate thing is that these pointers, as a rule, cannot be updated in an atomic fashion. For 32-bit architectures, it is typical to write a 32-bit variable that is atomic. But “thick pointers” contain 3 integer sizes., therefore, if you have a code that expects the pointer to have an atomic value, you can get into trouble. Because in order to do some of these checks, you have to look at the current address, and then look at the dimensions, and then you may have to increase them, and so on and so forth. Thus, it can cause very subtle errors if you use code that attempts to draw parallels between normal and thick pointers. Thus, you can use Fat pointers in some cases, like Electroc fences , but the side effects of their use are so significant that in normal practice these approaches are not used.

And now we'll talk about checking the boundaries with respect to the structure of the shadow data. The basic idea of ​​the structure is that you know how large each object that you are going to place, that is, you know the size that you need to reserve for this object. So, for example, if you have a pointer that you call using the malloc function , you need to specify the size of the object: char xp = malloc (size) .



If you have something like a static variable, like this char p [256] , the compiler can automatically figure out what the boundaries for its placement should be.

Therefore, for each of these pointers, you need to somehow insert two operations. This is mainly arithmetic, such as q = p + 7, or something similar. This insertion is done by dereference of the reference type deref * q = 'q' . You may wonder why you can not rely on the link when pasting? Why do we need to perform these arithmetic operations? The fact is that when using C and C ++, you have a pointer pointing to one pass to the allowed end of the object to the right, after which you use it as a stop condition. So, you go to the object and as soon as you reach this final pointer, you will actually stop the cycle or interrupt the operation.

So, if we ignore arithmetic, we always cause a serious error in which the pointer goes beyond the boundaries, which can actually disrupt the work of many applications. So we can’t just insert a link, because how do you know that this is happening beyond the established limits? Arithmetic allows us to say whether it is true or not, and here everything will be legal and correct. Because this wedging with arithmetic allows you to track where the pointer is relative to its original baseline.

So the next question is: how do we actually implement the verification of boundaries? Because we need to somehow match the specific address of the pointer with some type of boundary information for this pointer. And so many of your previous decisions use things like, for example, a hash table, or a tree, which allows for the right search. So, given the pointer's address, I do some searching in this data structure and find out what boundaries it has. Given these boundaries, I decide whether I can allow the action to occur or not. The problem is that this is a slow search, because these data structures are branching, and when examining a tree, you need to examine a bunch of such branches until you find the desired value. And even if it is a hash table, you have to go through the code chains and so on. In this way, we need to define a very efficient data structure that would track their boundaries, one that would make this check very simple and clear. So let's just get to that right now.

But before we do this, let me tell you very briefly how the buddy memory allocation approach works . Because this is one of the things that people often ask about.
Buddy memory allocation divides memory into partitions with a multiple of a power of 2, and attempts to allocate memory requests to them. Consider how it works. Initially, buddy allocation processes unallocated memory as one large block — this is the top 128-bit rectangle. Then, when you request a smaller block for dynamic allocation, it tries to divide this address space into parts with a multiple of 2 until it finds a block sufficient for your needs.

Suppose a request of type a = malloc (28) arrived, i.e. a request for allocation of 28 bytes. We have a block of 128 bytes, which is too wasteful to allocate for this request. Therefore, our block is divided into two blocks of 64 bytes - from 0 to 64 bytes and from 64 bytes to 128 bytes. And this size is also great for our request, so buddy again divides a block of 64 bytes into 2 parts and receives 2 blocks of 32 bytes each.



Less is impossible, because 28 bytes will not fit, and 32 is the most suitable minimum size. So now this 32-byte block will be allocated to our address a. Suppose we have another request for the value b = malloc (50) . Buddy checks the allocated blocks, and since 50 is more than half of 64, but less than 64, places the value of b in the rightmost block.

Finally, we have another request for 20 bytes: c = malloc (20) , this value is placed in the middle block.



The buddy has an interesting property: when you free up memory in a block, and a block of the same size is located next to it, after releasing both blocks, buddy combines two empty neighboring blocks into one.



For example, when we give the command free © , we will release the middle block, but the union will not happen, so the block will be still busy next to it. But after the release of the first block with the free command (a)both units will merge into one. Then, if we release the value of b, the neighboring blocks will merge again and we will get a whole block of 128 bytes in size, as it was at the very beginning. The advantage of this approach is that you can easily find out where the buddy is by simple arithmetic and define the limits of memory. Thus, memory allocation works at the Buddy memory allocation approach .

In all my lectures, the question is often asked, isn't this approach wasteful? Imagine that at first I had a request for 65 bytes, I would have to allocate an entire block of 128 bytes for it. Yes, it is wasteful, in fact, you do not have a dynamic memory and you can no longer allocate resources in the same block. But again, this is a compromise, because it is very easy to make a calculation, how to make a merge and the like. So if you want a more accurate allocation of memory, you need to use a different approach.

So what does the Buggy bounce checking (BBC) system do?



It performs several tricks, one of which is the division of a block of memory into 2 parts, in one of which the object is located, and in the second - an addition to it. Thus, we have 2 types of borders - object borders and memory distribution borders. The advantage is that there is no need to store the base address, and a quick search is possible using a linear table.

All of our distribution sizes are 2 to the power n , where n is an integer. This 2n principle is called power of two.. Therefore, we do not need many bits to imagine how large a particular size of distribution is. For example, if the cluster size is 16, then you just need to select 4 bits - this is the notion of logarithm, that is, 4 is an exponent n , into which you need to build the number 2 to get 16.

This is a fairly economical approach to memory allocation, because The minimum number of bytes is used, but it must be a multiple of 2, that is, you can have 16 or 32, but not 33 bytes. In addition, Buggy bounce checking allows you to store information about the boundary values ​​in a linear array (1 byte per write) and allows you to allocate memory in 1 slot of 16 bytes. allocate memory with slot granularity. What does it mean?



If we have a 16-byte slot where we are going to put the value p = malloc (16) , then the value in the table will look like table [p / slot.size] = 4 .



Suppose we now need to allocate a size of 32 bytes, p = malloc (32) . We need to update the table of boundaries in accordance with the new size. And this is done twice: first as table [p / slot.size] = 5 , and then as table [(p / slot.size) + 1] = 5- the first time for the first slot, which is distributed under this memory, and the second time - for the second slot. So we allocate 32 bytes of memory. This is the size distribution log. Thus, for two memory allocation slots, the boundary table is updated twice. It's clear? This example is intended for people who doubt whether the logs and tables make sense or not. Because the tables are multiplied every time the memory is allocated.

Let's see what happens with the table of boundaries. Suppose we have a code C, which looks like this: p '= p + i , that is, the pointer p' is obtained from p by adding some variable i . So how do we get the size of memory allocated to p? To do this, you look at the table using the following logical conditions:

size = 1 << table [p >> log of slot_size]



On the right we have the size of the data distributed for p , which should be 1. Then you shift it to the left and look at table, take this pointer size, then move to the right where the log of the slot size table is located. If the arithmetic works, it means that we have correctly linked the pointer to the table of boundaries. That is, the pointer size must be greater than 1, but less than the size of the slot. On the left we have the value, and on the right - the size of the slot, and the value of the pointer is located between them.

Suppose that the pointer size is 32 bytes, then in the table, inside the straight brackets, we will have the number 5.

Suppose we want to find the base keyword of this pointer: base = p & n (size - 1) . What we are going to do gives us a certain mass, and this mass will allow us to restore the base located here. Imagine that our size is 16, in binary code it is 16 = ... 0010000. Ellipsis means that there are many more zeros there, but we are interested in this unit and zeros behind it. If we consider (16 -1), then it looks something like this: (16 - 1) = ... 0001111. In binary code, the inversion of this will look like this: ~ (16-1) ... 1110000.





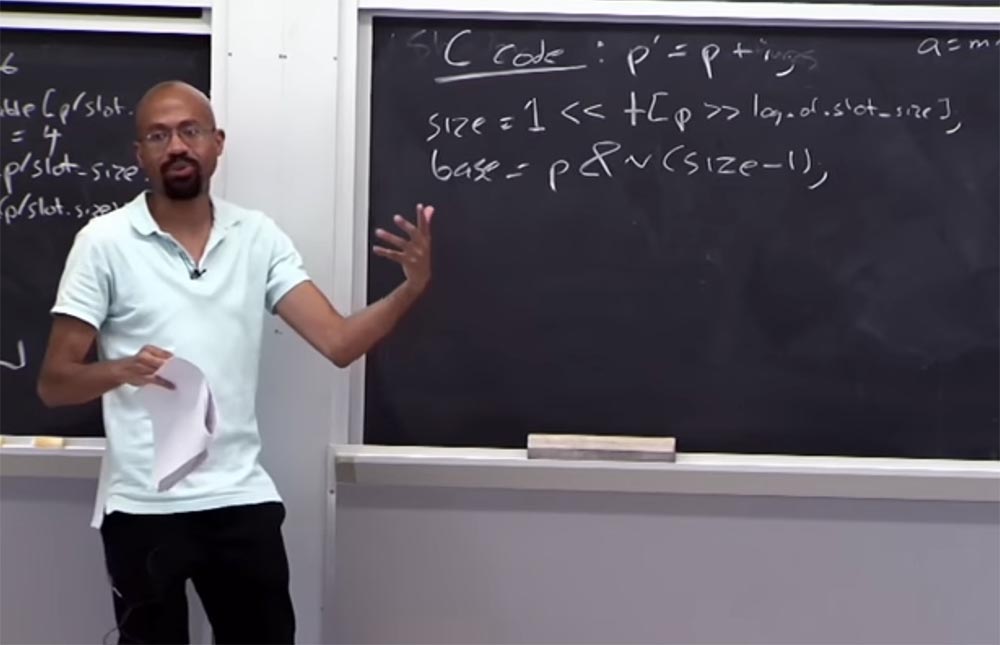
Thus, this thing allows us to basically clear the bit, which will essentially be taken out of the current pointer and give us its base. Due to this, it will be very easy for us to check whether this pointer is within the borders. So we can simply check that (p ')> = base and whether the value ( p' - base) is smaller than the selected size size .



This is a fairly simple thing, allowing you to find out if the pointer is in memory. I'm not going to go into details, suffice it to say that all binary arithmetic is resolved in the same way. Such tricks allow you to avoid more complex calculations.

There is another, fifth property Buggy bounce checking- It uses a virtual memory system to prevent the border from relegation to the pointer. The basic idea is that if we have such arithmetic for the pointer, with the help of which we determine the out-of-bounds, then we can set high-order bits for the pointer.



By doing so, we guarantee that pointer dereferencing will not cause hardware problems. By itself, setting a high order bit to a high order bit does not cause problems; a pointer dereference can cause a problem.


Full version of the course is available here .

Thank you for staying with us. Do you like our articles? Want to see more interesting materials? Support us by placing an order or recommending to friends, 30% discount for Habr's users on a unique analogue of the entry-level servers that we invented for you: The whole truth about VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps from $ 20 or how to share the server? (Options are available with RAID1 and RAID10, up to 24 cores and up to 40GB DDR4).

Dell R730xd 2 times cheaper? Only we have 2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV from $ 249 in the Netherlands and the USA! Read aboutHow to build the infrastructure of the building. class c using servers Dell R730xd E5-2650 v4 worth 9000 euros for a penny?