ICFPC 2012 Competition Objective: Robot and λ
- Transfer
Just a few hours ago, the ICFPC-2012 contest began, which will last all weekend . I decided to transfer the task for this contest in the hope that one of the interested people will have time to take part.
The task is quite understandable, so go for it.
Changes were made to the task: water , teleporters , beard and super stones .
Lambda mines discovered in Scotland! Your task is to be able to make a program for the robot by reading the mine map.
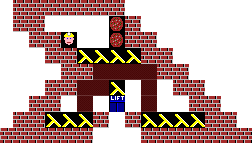
Link to a beautiful simulator: icfp.stbuehler.de/icfp2012
A map is a grid of m × n cells, coordinate (1,1) is located at the bottom and left.
Each cell contains one of the following characters:
Nothing can penetrate the wall. Nothing can go beyond the m × n field. A robot can dig earth, collect λ and move stones. The stones are falling. Stones can kill a robot.
An example of an initial state:
If the coordinates of the robot (x, y):
You can move into a cage with an open exit, into an empty cage, into a cage with earth and a cage with λ. You can still move (only left and right) into the cage with a stone, if there is an empty place behind the stone. After leaving the cage, the robot always leaves a void in the cage.
After the movement of the robot passes the simulation step. During this stage, the old state is always read and written to the new one. In the following order in coordinates: (1, 1), (2, 1), ..., (n, 1), (1, 2) ... (n, m).
Rules are checked in order, from top to bottom. If one worked, then the next will not work.
If there is no more λ on the card, all closed outputs open.
If a robot stood under a stone that just fell, the robot breaks down, this is a defeat.
In one simulation step, the stones fall 1 cell down.
Sometimes stones from different sides can fall into one cell. In this case, 1 stone now lies in this cell.
Input with stdin, output to stdout
If some lines are shorter than the maximum length of the line, then they are considered padded with spaces on the right.
There are no open exits on each map at the beginning. There is exactly 1 robot and exactly 1 closed output.
The card can be 1000 × 1000 or more.
For each step -1
For the collected λ +25
For the collected λ at the time of the execution of the A +25 command
For the collected λ at the time of reaching the output +50
Script for testing your options for passing test cards: validator
The program should run on 32bit Debian-linux with 1 Gb RAM.
After 150 seconds, the program receives SIGINT, after which it has 10 seconds to output a response.
After these 10 seconds, SIGKILL and 0 points.
During the competition there will be from 1 to 4 rule changes.
Details in English: icfpcontest2012.wordpress.com
Some mines began to flood!
Now, after the description of the map, an empty line can go and then 3 parameters (1 per line):
Water 0
Flooding 0
Waterproof 10
(0, 0, 10) - default values.
Water indicates the initial value of the water level (remember that we count the coordinates from 1, and the water level may be 0).
Flooding - the rate of arrival of water. If 0 - water does not arrive at all. If N> 0, then exactly after N steps the water level increases by 1.
Waterproof - the level of protection of the robot, how many steps without diving it can go under water. As soon as it emerges, the step counter resets and you can dive again.
A robot is considered to be under water if its y coordinate <= water level.
If the robot spends more than Waterproof steps underwater, it breaks.
Teleports have been added to the game (called diving boards in the dock). The input of the teleport is indicated by the letters A..I, the output of the teleport is the numbers 1..9.
After entering the teleport, the entrance of the teleport and its exit disappear.
Which entrance leads to which exit is described after the card with phrases:
Trampoline A targets 1
Trampoline B targets 1
Trampoline C targets 2
Added beard - W and razor - ! . At the end of the map it’s now written how many razors the razor has with it and how fast the beard grows:
Growth 15
Razors 2
The growth value (g) by default is 25, the number of razors is 0.
Every g steps, the beard fills 8 neighboring cells if they are empty (that is, including the diagonal).
A razor is the only way to deal with a beard. After executing the S command, a razor (if the robot has one) is applied and cleans the beard of 8 neighboring cells.
Added @ - stones of higher order, inside which λ are hidden. When falling from any height, the stone breaks and λ appears in its place.
Note that the task is very similar to the complicated Boulder Dash, the passage of which, in the general case, as it is proved, is an NP-complete task.
The proof is quite simple: there are labyrinths whose solution is equivalent to finding a Hamiltonian cycle in a graph, and this is a well-known problem: wiki Hamiltonian cycle
The task is quite understandable, so go for it.
Changes were made to the task: water , teleporters , beard and super stones .
Lambda mines discovered in Scotland! Your task is to be able to make a program for the robot by reading the mine map.

Link to a beautiful simulator: icfp.stbuehler.de/icfp2012
Basic Rules
- The robot skips any characters unknown to it (and only L, R, U, D, W, A are known to it.
- If the Robot cannot execute the command, it simply does nothing this move.
- After the robot moves, the map is updated according to the rules described below.
- After updating the map, the conditions for completion are checked.
Card description
A map is a grid of m × n cells, coordinate (1,1) is located at the bottom and left.
Each cell contains one of the following characters:
- R - Robot
- * - stone
- L - closed exit
- . - land
- # - wall
- \ - λ
- O - open output
- " " - space, empty cell
Nothing can penetrate the wall. Nothing can go beyond the m × n field. A robot can dig earth, collect λ and move stones. The stones are falling. Stones can kill a robot.
An example of an initial state:
#######
#..***#
#..\\\#
# ..**#
#.*.*\#
LR....#
#######Robot Commands
If the coordinates of the robot (x, y):
- L - left, in (x-1, y)
- R - to the right, in (x + 1, y)
- U - up, in (x, y + 1)
- D - down, in (x, y-1)
- W - wait, do nothing
- A - abort mine exploration
You can move into a cage with an open exit, into an empty cage, into a cage with earth and a cage with λ. You can still move (only left and right) into the cage with a stone, if there is an empty place behind the stone. After leaving the cage, the robot always leaves a void in the cage.
Map update (simulation)
After the movement of the robot passes the simulation step. During this stage, the old state is always read and written to the new one. In the following order in coordinates: (1, 1), (2, 1), ..., (n, 1), (1, 2) ... (n, m).
Rules are checked in order, from top to bottom. If one worked, then the next will not work.
- There is a void under the stone - the stone falls 1 cell down.
- There is a stone under the stone, empty on the right and empty on the lower right - the stone falls diagonally to the right.
- There is a stone under the stone, empty on the left and empty at the bottom left - the stone falls diagonally to the left.
- Under the stone - λ, empty on the right and empty on the bottom right - the stone falls diagonally to the right.
- The remaining cells do not move.
If there is no more λ on the card, all closed outputs open.
If a robot stood under a stone that just fell, the robot breaks down, this is a defeat.
In one simulation step, the stones fall 1 cell down.
Sometimes stones from different sides can fall into one cell. In this case, 1 stone now lies in this cell.
Completion conditions
- Robot Enters Open Lift - WIN
- The robot executed command A - WIN
- Stone Crushed Robot - LOSE
Input Output
Input with stdin, output to stdout
If some lines are shorter than the maximum length of the line, then they are considered padded with spaces on the right.
There are no open exits on each map at the beginning. There is exactly 1 robot and exactly 1 closed output.
The card can be 1000 × 1000 or more.
Scoring Points
For each step -1
For the collected λ +25
For the collected λ at the time of the execution of the A +25 command
For the collected λ at the time of reaching the output +50
Script for testing your options for passing test cards: validator
Limits
The program should run on 32bit Debian-linux with 1 Gb RAM.
After 150 seconds, the program receives SIGINT, after which it has 10 seconds to output a response.
After these 10 seconds, SIGKILL and 0 points.
During the competition there will be from 1 to 4 rule changes.
Details in English: icfpcontest2012.wordpress.com
First rule change: water
Some mines began to flood!
Now, after the description of the map, an empty line can go and then 3 parameters (1 per line):
Water 0
Flooding 0
Waterproof 10
(0, 0, 10) - default values.
Water indicates the initial value of the water level (remember that we count the coordinates from 1, and the water level may be 0).
Flooding - the rate of arrival of water. If 0 - water does not arrive at all. If N> 0, then exactly after N steps the water level increases by 1.
Waterproof - the level of protection of the robot, how many steps without diving it can go under water. As soon as it emerges, the step counter resets and you can dive again.
A robot is considered to be under water if its y coordinate <= water level.
If the robot spends more than Waterproof steps underwater, it breaks.
Second rule change: teleporters
Teleports have been added to the game (called diving boards in the dock). The input of the teleport is indicated by the letters A..I, the output of the teleport is the numbers 1..9.
After entering the teleport, the entrance of the teleport and its exit disappear.
Which entrance leads to which exit is described after the card with phrases:
Trampoline A targets 1
Trampoline B targets 1
Trampoline C targets 2
Third rule change: biomass and razors
Added beard - W and razor - ! . At the end of the map it’s now written how many razors the razor has with it and how fast the beard grows:
Growth 15
Razors 2
The growth value (g) by default is 25, the number of razors is 0.
Every g steps, the beard fills 8 neighboring cells if they are empty (that is, including the diagonal).
A razor is the only way to deal with a beard. After executing the S command, a razor (if the robot has one) is applied and cleans the beard of 8 neighboring cells.
Last rule change: higher order stones
Added @ - stones of higher order, inside which λ are hidden. When falling from any height, the stone breaks and λ appears in its place.
About difficulty assessment
Note that the task is very similar to the complicated Boulder Dash, the passage of which, in the general case, as it is proved, is an NP-complete task.
The proof is quite simple: there are labyrinths whose solution is equivalent to finding a Hamiltonian cycle in a graph, and this is a well-known problem: wiki Hamiltonian cycle
