June 21, 2012 at 11:26Implementation of the principal component method in C #
Hello. This week, in a machine learning course, Professor Andrew Ng told the audience about the principal component method with which you can reduce the dimension of the feature space of your data. But unfortunately he did not talk about the method of calculating the eigenvectors and eigenvalues of the matrix, he simply said that it was difficult and advised using the matlab / octave function [USV] = svd (a).
For my project, I needed an implementation of this method in c #, which I did today. The method of main components itself is very elegant and beautiful, and if you do not understand the mathematics that lies behind all this, then this can be called shamanism. The problem with calculating the eigenvectors of the matrix is that there is no fastway to calculate their exact values, so you have to get out. I want to talk about one of these ways to get out, and I will also give c # code that performs this procedure. I ask for cat.
Part one: initialization of the algorithm. The input is an array of data, as well as the dimension of the space to which the data must be reduced.
Part two: reducing the dimension of the input vector. A vector is fed to the input, of a dimension as in the data array used in the initialization step; the output is a vector of lower dimension (or the projection of the input vector onto an orthonormal basis formed by a sample of eigenvectors).
Part Three: restoring the dimension of a vector (of course with loss of information). The input is a vector of dimension equal to that to which we reduced the vectors; the output is a vector of the original dimension.
As you can see, all the computational complexity is in the initialization step when calculating the covariance matrix and eigenvectors. I will not dwell on the calculation of the covariance matrix, because it is calculated naively by definition. Having studied several algorithms for calculating the eigenvectors of the matrix, I settled on the iterative method of QR decomposition. It has a significant restriction, it gives a more or less accurate result only for symmetric matrices, but we are lucky :), the covariance matrix is just that. The second limitation of this algorithm is that the matrix must be full-rank .
The iterative QR method of searching for eigenvectors obviously uses QR decomposition , so first you have to implement this process. To implement this process, the Graham-Schmidt algorithm was chosen .
To do this, we need a function that calculates the projection of the vector a onto the vector b :,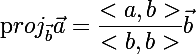
where <> - denote the scalar product of vectors.
I will not dwell on even simpler functions, such as ScalarVectorProduct, so that the code size in the text does not exceed the critical norm.
So actually the actual QR decomposition procedure IList DecompositionGS (double [] [] a) receives a matrix input, and produces two matrices in response:
First of all, we break the matrix into columns and write them to the av list :
We initialize two auxiliary lists:
These are the same lists of the same name used in the algorithm diagram:
After initialization, the first u and e are calculated, we continue to calculate the following values in a loop:
And finally, we generate data in the output format:
Hurrah! Now we need a test for this:
The Helper.AreEqualMatrices function compares element-wise matrices up to the third parameter.
The iterative QR method is based on a wonderful theorem, the essence of which is that if you initialize the matrix A zero as
well as repeat the following process infinitely many times:
and then multiply all the obtained Qs , the result is a matrix, in the columns of which there will be eigenvectors of the original matrix, the values of which will be the more accurate, the longer the process takes. In other words, as the number of iterations tends to infinity, the product
will tend to the exact values of the eigenvectors. At the same time, the latter 
will contain the eigenvalues of the matrix, approximate of course, on the main diagonal. I remind you that this algorithm more or less accurately works only for symmetric matrices.
So, the QR iteration method IList EigenVectorValuesExtractionQRIterative (double [] [] a, double accuracy, int maxIterations) gets the input past the matrix itself, as well as a few more parameters:
At the output we get two matrices:
So, we’ll start writing an algorithm, first we’ll create matrices that will contain eigenvectors and eigenvalues of the original matrix:
And run the loop until the algorithm stops:
Generate the output:
And of course the test:
It is worth noting that eigenvectors can change direction from iteration to iteration, which will be seen by changing the signs of their coordinates, but it is obvious that this is not essential.
Now everything is ready for the implementation of the subject.
The hidden parameter of the model (class) will be a subset of the eigenvectors of the covariance matrix from the original data:
The designer accepts an input data array and dimension to which the attribute space should be reduced, as well as parameters for QR decomposition. Inside, the covariance matrix is computed and the first few eigenvectors are taken. In general, there is a way to choose the optimal number of eigenvectors for the desired information loss parameter, i.e. to which dimension you can reduce the space, having lost no more than a fixed percentage of information, but I omit this step, you can listen about it in the lecture by Andrew Ng on the course website.
Then we implement the direct and inverse transformation by formulas from the beginning of the article.
For testing, we’ll come up with a small array of data, and checking the values on the matlab (using the code from home at PCA =), we will write a class for testing:
For my project, I needed an implementation of this method in c #, which I did today. The method of main components itself is very elegant and beautiful, and if you do not understand the mathematics that lies behind all this, then this can be called shamanism. The problem with calculating the eigenvectors of the matrix is that there is no fastway to calculate their exact values, so you have to get out. I want to talk about one of these ways to get out, and I will also give c # code that performs this procedure. I ask for cat.
Principal component method (so far without code)
Part one: initialization of the algorithm. The input is an array of data, as well as the dimension of the space to which the data must be reduced.
- The covariance matrix is calculated (this matrix has a wonderful property - it is symmetric, this is very useful to us)
- The eigenvectors of the matrix are calculated
- The first en of eigenvectors are selected, where en is the same dimension to which it is necessary to reduce the dimension of the feature space; selected vectors can be written vertically and assembled into a matrix
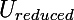
Part two: reducing the dimension of the input vector. A vector is fed to the input, of a dimension as in the data array used in the initialization step; the output is a vector of lower dimension (or the projection of the input vector onto an orthonormal basis formed by a sample of eigenvectors).
- By scalarly multiplying the input vector by all vectors from the sample of eigenvectors, we obtain a reduced vector:
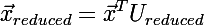
Part Three: restoring the dimension of a vector (of course with loss of information). The input is a vector of dimension equal to that to which we reduced the vectors; the output is a vector of the original dimension.
- If the matrix is transposed, 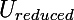then there will be as many rows in it as the dimension of the input vector in the previous step, and the desired vector is restored by the formula: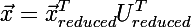
As you can see, all the computational complexity is in the initialization step when calculating the covariance matrix and eigenvectors. I will not dwell on the calculation of the covariance matrix, because it is calculated naively by definition. Having studied several algorithms for calculating the eigenvectors of the matrix, I settled on the iterative method of QR decomposition. It has a significant restriction, it gives a more or less accurate result only for symmetric matrices, but we are lucky :), the covariance matrix is just that. The second limitation of this algorithm is that the matrix must be full-rank .
QR decomposition
The iterative QR method of searching for eigenvectors obviously uses QR decomposition , so first you have to implement this process. To implement this process, the Graham-Schmidt algorithm was chosen .
To do this, we need a function that calculates the projection of the vector a onto the vector b :,
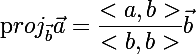where <> - denote the scalar product of vectors.public static double[] VectorProjection(double[] a, double[] b)
{
double k = ScalarVectorProduct(a, b)/ScalarVectorProduct(b, b);
return ScalarToVectorProduct(k, b);
}
I will not dwell on even simpler functions, such as ScalarVectorProduct, so that the code size in the text does not exceed the critical norm.
So actually the actual QR decomposition procedure IList
- the first contains in its columns an orthonormal basis such that
; - the second matrix will be upper triangular .
First of all, we break the matrix into columns and write them to the av list :
List av = new List();
foreach (double[] vector in DecomposeMatrixToColumnVectors(a))
{
av.Add(vector);
}
We initialize two auxiliary lists:
List u = new List();
u.Add(av[0]);
List e = new List();
e.Add(ScalarToVectorProduct(1 / NormOfVector(u[0]), u[0]));
These are the same lists of the same name used in the algorithm diagram:
After initialization, the first u and e are calculated, we continue to calculate the following values in a loop:
for (int i = 1; i < a.Length; i++)
{
double[] projAcc = new double[a.Length];
for (int j = 0; j < projAcc.Length; j++)
{
projAcc[j] = 0;
}
for (int j = 0; j < i; j++)
{
double[] proj = VectorProjection(av[i], e[j]);
for (int k = 0; k < projAcc.Length; k++)
{
projAcc[k] += proj[k];
}
}
double[] ui = new double[a.Length];
for (int j = 0; j < ui.Length; j++)
{
ui[j] = a[j][i] - projAcc[j];
}
u.Add(ui);
e.Add(ScalarToVectorProduct(1/NormOfVector(u[i]), u[i]));
}
And finally, we generate data in the output format:
double[][] q = new double[a.Length][];
for (int i = 0; i < q.Length; i++)
{
q[i] = new double[a.Length];
for (int j = 0; j < q[i].Length; j++)
{
q[i][j] = e[j][i];
}
}
double[][] r = new double[a.Length][];
for (int i = 0; i < r.Length; i++)
{
r[i] = new double[a.Length];
for (int j = 0; j < r[i].Length; j++)
{
if (i >= j)
{
r[i][j] = ScalarVectorProduct(e[j], av[i]);
}
else {
r[i][j] = 0;
}
}
}
r = Transpose(r);
List res = new List();
res.Add(q);
res.Add(r);
return res;
Hurrah! Now we need a test for this:
[Test(Description = "Test of QRDecompositionGS")]
public void QRDecompositionGSTest()
{
double[][] a = new double[][]
{
new double[] {12, -51, 4},
new double[] {6, 167, -68},
new double[] {-4, 24, -41}
};
IList res = LinearAlgebra.QRDecompositionGS(a);
double[][] expQ = new double[][]
{
new double[] {6.0/7, -69.0/175, -58.0/175},
new double[] {3.0/7, 158.0/175, 6.0/175},
new double[] {-2.0/7, 6.0/35, -33.0/35}
};
double[][] expR = new double[][]
{
new double[] {14, 21, -14},
new double[] {0, 175, -70},
new double[] {0, 0, 35}
};
Assert.True(Helper.AreEqualMatrices(expQ, res[0], 0.0001), "expQ != Q");
Assert.True(Helper.AreEqualMatrices(expR, res[1], 0.0001), "expR != R");
}
The Helper.AreEqualMatrices function compares element-wise matrices up to the third parameter.
Iterative QR Method
The iterative QR method is based on a wonderful theorem, the essence of which is that if you initialize the matrix A zero as
and then multiply all the obtained Qs , the result is a matrix, in the columns of which there will be eigenvectors of the original matrix, the values of which will be the more accurate, the longer the process takes. In other words, as the number of iterations tends to infinity, the product
So, the QR iteration method IList
- double accuracy - the accuracy we want to achieve, the algorithm will stop if changes in the values of eigenvectors are no more than this value;
- int maxIterations - maximum number of iterations.
At the output we get two matrices:
- the first contains in its columns the eigenvectors of the matrix a ;
- the second matrix on its main diagonal contains the eigenvalues of the matrix a .
So, we’ll start writing an algorithm, first we’ll create matrices that will contain eigenvectors and eigenvalues of the original matrix:
double[][] aItr = a;
double[][] q = null;
And run the loop until the algorithm stops:
for (int i = 0; i < maxIterations; i++)
{
IList qr = QRDecompositionGS(aItr);
aItr = MatricesProduct(qr[1], qr[0]);
if (q == null)
{
q = qr[0];
}
else {
double[][] qNew = MatricesProduct(q, qr[0]);
bool accuracyAcheived = true;
for (int n = 0; n < q.Length; n++)
{
for (int m = 0; m < q[n].Length; m++)
{
if (Math.Abs(Math.Abs(qNew[n][m]) - Math.Abs(q[n][m])) > accuracy)
{
accuracyAcheived = false;
break;
}
}
if (!accuracyAcheived)
{
break;
}
}
q = qNew;
if (accuracyAcheived)
{
break;
}
}
}
Generate the output:
List res = new List();
res.Add(q);
res.Add(aItr);
return res;
And of course the test:
[Test(Description = "Test of Eigen vectors extraction")]
public void EigenVectorExtraction()
{
double[][] a = new double[][]
{
new double[] {1, 2, 4},
new double[] {2, 9, 8},
new double[] {4, 8, 2}
};
IList ev = LinearAlgebra.EigenVectorValuesExtractionQRIterative(a, 0.001, 1000);
double expEV00 = 15.2964;
double expEV11 = 4.3487;
double expEV22 = 1.0523;
Assert.AreEqual(expEV00, Math.Round(Math.Abs(ev[1][0][0]), 4));
Assert.AreEqual(expEV11, Math.Round(Math.Abs(ev[1][1][1]), 4));
Assert.AreEqual(expEV22, Math.Round(Math.Abs(ev[1][2][2]), 4));
}
It is worth noting that eigenvectors can change direction from iteration to iteration, which will be seen by changing the signs of their coordinates, but it is obvious that this is not essential.
Implementation of the principal component method
Now everything is ready for the implementation of the subject.
The hidden parameter of the model (class) will be a subset of the eigenvectors of the covariance matrix from the original data:
private IList _eigenVectors = null;
The designer accepts an input data array and dimension to which the attribute space should be reduced, as well as parameters for QR decomposition. Inside, the covariance matrix is computed and the first few eigenvectors are taken. In general, there is a way to choose the optimal number of eigenvectors for the desired information loss parameter, i.e. to which dimension you can reduce the space, having lost no more than a fixed percentage of information, but I omit this step, you can listen about it in the lecture by Andrew Ng on the course website.
internal DimensionalityReductionPCA(IList dataSet, double accuracyQR, int maxIterationQR, int componentsNumber)
{
double[][] cov = BasicStatFunctions.CovarianceMatrixOfData(dataSet);
IList eigen = LinearAlgebra.EigenVectorValuesExtractionQRIterative(cov, accuracyQR, maxIterationQR);
IList eigenVectors = LinearAlgebra.DecomposeMatrixToColumnVectors(eigen[0]);
if (componentsNumber > eigenVectors.Count)
{
throw new ArgumentException("componentsNumber > eigenVectors.Count");
}
_eigenVectors = new List();
for (int i = 0; i < componentsNumber; i++)
{
_eigenVectors.Add(eigenVectors[i]);
}
}
Then we implement the direct and inverse transformation by formulas from the beginning of the article.
public double[] Transform(double[] dataItem)
{
if (_eigenVectors[0].Length != dataItem.Length)
{
throw new ArgumentException("_eigenVectors[0].Length != dataItem.Length");
}
double[] res = new double[_eigenVectors.Count];
for (int i = 0; i < _eigenVectors.Count; i++)
{
res[i] = 0;
for (int j = 0; j < dataItem.Length; j++)
{
res[i] += _eigenVectors[i][j]*dataItem[j];
}
}
return res;
}
public double[] Reconstruct(double[] transformedDataItem)
{
if (_eigenVectors.Count != transformedDataItem.Length)
{
throw new ArgumentException("_eigenVectors.Count != transformedDataItem.Length");
}
double[] res = new double[_eigenVectors[0].Length];
for (int i = 0; i < res.Length; i++)
{
res[i] = 0;
for (int j = 0; j < _eigenVectors.Count; j++)
{
res[i] += _eigenVectors[j][i]*transformedDataItem[j];
}
}
return res;
}
Testing
For testing, we’ll come up with a small array of data, and checking the values on the matlab (using the code from home at PCA =), we will write a class for testing:
[TestFixture(Description = "Test of DimensionalityReductionPCA")]
public class DimensionalityReductionPCATest
{
private IList _data = null;
private IDataTransformation _transformation = null;
private double[] _v = null;
[SetUp]
public void SetUp()
{
_v = new double[] { 1, 0, 3 };
_data = new List()
{
new double[] {1, 2, 23},
new double[] {-3, 17, 5},
new double[] {13, -6, 7},
new double[] {7, 8, -9}
};
_transformation = new DimensionalityReductionPCA(_data, 0.0001, 1000, 2);
}
[Test(Description = "Test of DimensionalityReductionPCA transform")]
public void DimensionalityReductionPCATransformTest()
{
double[] reduced = _transformation.Transform(_v);
double[] expReduced = new double[] {-2.75008, 0.19959};
Assert.IsTrue(Helper.AreEqualVectors(expReduced, reduced, 0.001));
double[] reconstructed = _transformation.Reconstruct(reduced);
double[] expReconstructed = new double[] {-0.21218, -0.87852, 2.60499};
Assert.IsTrue(Helper.AreEqualVectors(expReconstructed, reconstructed, 0.001));
}
References
- machine learning course
- article that describes the iterative QR method
- a bunch of Wikipedia links in the text of the article