AI, practical course. Neural network overview for image classification
- Transfer
This article provides an accessible theoretical overview of convolutional neural networks (Convolutional Neural Network, CNN) and explains their application to the problem of image classification.
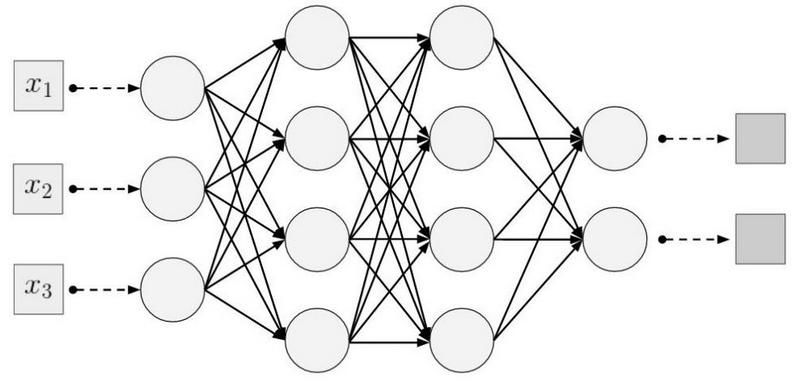
The term "image processing" refers to a wide class of tasks, the input data for which are images, and the output can be both images and sets of associated characteristics. There are many options: classification, segmentation, annotation, object detection, etc. In this article, we explore the classification of images not only because it is the simplest task, but also because it underlies many other tasks.
The general approach to the problem of image classification consists of the following two steps:
The generally accepted sequence of operations uses simple models such as multi-level perception (MultiLayer Perceptron, MLP), the Support Vector Machine (SVM), the k-nearest-neighbor method, and logistic regression over hand-created features. Characteristics are generated using various transformations (for example, rendering in shades of gray and defining thresholds) and descriptors, for example, oriented gradient histograms (Histogram of Oriented Gradients, HOG ) or scale-invariant feature transformations ( SIFT ), and etc.
The main limitation of the generally accepted methods is the participation of an expert who chooses a set and sequence of steps for generating features.
Over time, it was noticed that most of the feature generation techniques can be generalized using kernels (filters) - small matrices (usually 5 × 5), which are convolutions of the original images. Convolution can be viewed as a sequential two-step process:
The result of the convolution of the image and the kernel is called the feature map.
A more rigorous explanation is given in the corresponding chapter of the recently published book Deep Learning, by I. Goodfellow, I. Bengio, and A. Courville.
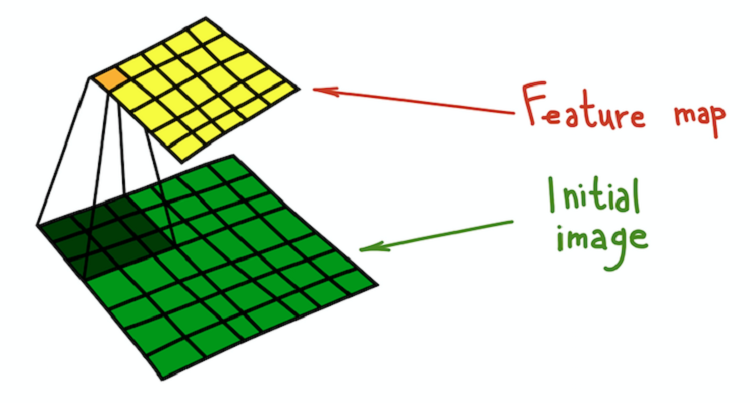
The process of core convolution (dark green) with the original image (green), which results in a feature map (yellow).
A simple example of a transformation that can be performed using filters is image blurring. Take a filter consisting of all units. It calculates the average value of the neighborhood defined by the filter. In this case, the neighborhood is a square section, but it can be cruciform or anything else. Averaging leads to loss of information about the exact position of objects, thus blurring the entire image. A similar intuitive explanation can be given for any manually created filter.
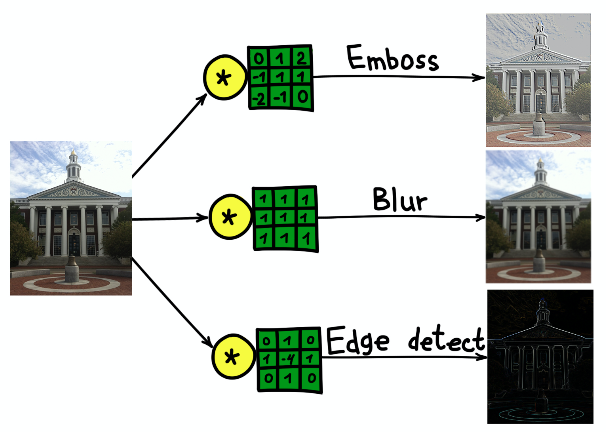
The result of the convolution of the image of the Harvard University building with three different cores.
The convolutional approach to the classification of images has several significant drawbacks:
Fortunately, learner filters were invented, which are the basic principle behind CNN. The principle is simple: We will train the filters applied to the description of the images in order to best perform their task.
CNN does not have one inventor, but one of the first instances of their use is LeNet-5 * in “Applying Gradient-Based Learning to the Document Recognition Problem” (Gradient-based Learning Applied to Document Recognition) by I. LeKun and others authors.
CNN kill two birds with one stone: there is no need for a preliminary definition of filters, and the learning process becomes transparent. The typical CNN architecture consists of the following parts:
Consider each part in more detail.
The convolutional layer is the main structural element of CNN. A convolutional layer has a set of characteristics:
Local (sparse) connectivity . In dense layers, each neuron is connected to each neuron of the previous layer (therefore, they were called dense). In the convolutional layer, each neuron is connected to only a small part of the neurons of the previous layer.
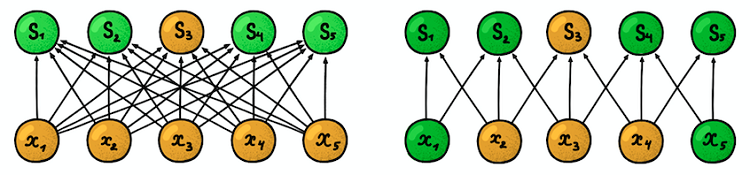
An example of a one-dimensional neural network. (left) Connection of neurons in a typical dense network, (right) Characteristics of local connectivity inherent in the convolutional layer. The images are taken from the book “Deep Learning” (Deep Learning) by I. Goodfellow and other authors. The
size of the area with which the neuron is connected, is called the filter size (filter length in the case of one-dimensional data, for example, time series, or width / height in the case of two-dimensional data, for example, images). In the figure on the right, the filter size is 3. The weights with which the connection is made are called a filter (a vector in the case of one-dimensional data and a matrix for two-dimensional). The pitch is the distance that the filter moves through the data (in the figure on the right, the pitch is 1). The idea of local connectivity is nothing more than a kernel moving a step. Each convolutional level neuron represents and implements one specific position of the nucleus, sliding along the original image.
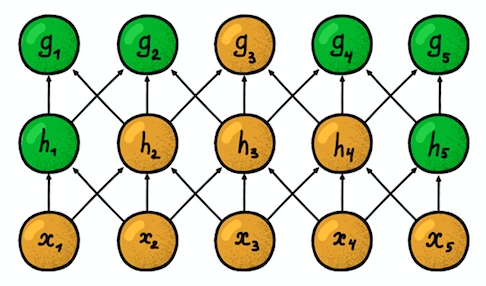
Two adjacent one-dimensional convolutional layers.
Another important property is the so-calledsusceptibility zone . It reflects the number of positions of the original signal that the current neuron can “see”. For example, the susceptibility zone of the first layer of the network shown in the figure is equal to the size of filter 3, since each neuron is connected to only three neurons of the original signal. However, on the second layer, the susceptibility zone is already equal to 5, since the neuron of the second layer aggregates three neurons of the first layer, each of which has a susceptibility zone 3. With increasing depth, the susceptibility zone grows linearly.
Shared parameters. Recall that in classical image processing, the same core slid across the entire image. Here the same idea applies. We fix only the filter size of the weighting factors for one layer and we will apply these weights to all neurons in the layer. This is equivalent to sliding the same core over the entire image. But the question may arise: how can we learn something with such a small number of parameters?

Dark arrows represent the same weights. (left) Normal MLP, where each weighting factor is a separate parameter, (right) Example of separation of parameters, where several weights indicate the same learning parameter
Spatial structure. The answer to this question is simple: we will train several filters in one layer! They are placed parallel to each other, thus forming a new dimension.
Let's pause for a while and explain the presented idea using the example of a 227 × 227 two-dimensional RGB image. Note that here we are dealing with a three-channel input image, which, in essence, means that we have three input images or three-dimensional input data.

The spatial structure of the input image
We will consider the dimensions of the channels as the depth of the image (note that this is not the same as the depth of the neural networks, which is equal to the number of layers of the network). The question is how to determine the core for this case.

An example of a two-dimensional core, essentially a three-dimensional matrix with an additional depth measurement. This filter gives convolution with the image; that is, it slides across the image in space, calculating scalar products. The
answer is simple, although it is still not obvious: let's make the core also three-dimensional. The first two measurements will remain the same (the width and height of the core), and the third dimension is always equal to the depth of the input data.
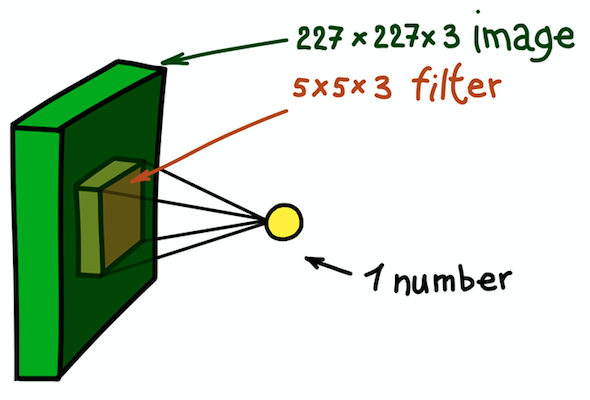
An example of spatial convolution step. The result of the scalar product of a filter and a small section of an image of 5 × 5 × 3 (i.e. 5 × 5 × 5 + 1 = 76 dimension of the scalar product + shift) is one number.
In this case, the entire 5 × 5 × 3 section of the original image is transformed one number, and the three-dimensional image itself will be transformed intofeature map ( activation card ). The feature map is a set of neurons, each of which calculates its own function taking into account the two basic principles discussed above: local connectivity (each neuron is associated with only a small part of the input data) and parameter sharing (all neurons use the same filter). Ideally, this feature map will be the same as the one already encountered in the example of the generally accepted network - it stores the results of the convolution of the input image and the filter.
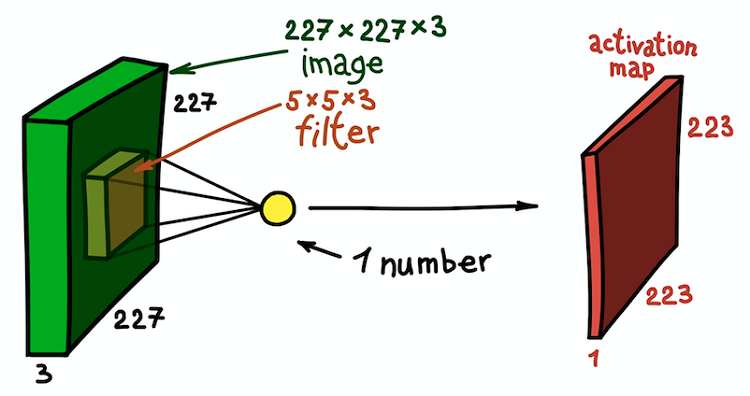
Character map as a result of convolution of the kernel with all spatial positions
Note that the depth of the feature map is 1, since we used only one filter. But nothing prevents us from using more filters; for example, 6. All of them will interact with the same input data and will work independently of each other. Go one step further and combine these feature maps. Their spatial dimensions are the same, since the dimensions of the filters are the same. Thus, the feature maps assembled together can be viewed as a new three-dimensional matrix, the depth dimension of which is represented by feature maps from different nuclei. In this sense, the RGB channels of the input image are nothing more than the three original feature maps.
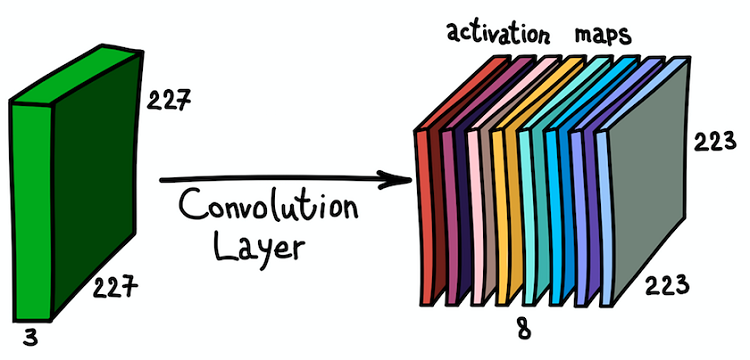
Parallel application of several filters to the input image and the resulting set of activation cards
Such an understanding of feature maps and their combination is very important, since, having realized this, we can expand the network architecture and install convolutional layers one on top of another, thereby increasing the area of susceptibility and enriching our classifier.
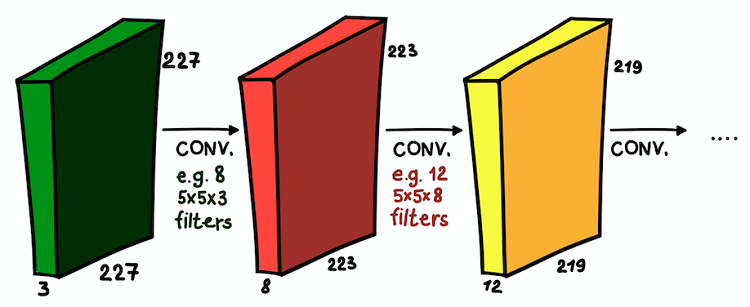
Convolutional layers laid over each other. In each layer, the sizes of filters and their number can vary.
Now we understand what a convolutional network is. The main purpose of these layers is the same as in the conventional approach - to detect significant features of the image. And, if in the first layer these signs can be very simple (the presence of vertical / horizontal lines), with the depth of the network their degree of abstraction increases (the presence of a dog / cat / person).
Convolutional layers are the main structural element of CNN. But there is another important and often used part - these are the subsample layers. In conventional image processing, there is no direct analogue, but a subsample can be considered as a different type of core. What is it?

Sample subsamples. (left) How subsampling changes spatial (but not channel!) sizes of data arrays, (right) Schematic diagram of subsampling
The subsample filters a portion of the neighborhood of each pixel of the input data with a certain aggregation function, for example, maximum, average, etc. The subsample is essentially the same as convolution, but the pixel combining function is not limited to scalar product. Another important difference is that the subsample works only in the spatial dimension. A characteristic feature of the subsample layer is that the step is usually equal to the size of the filter (the typical value is 2).
The subsample has three main objectives:
Convolutional layers and subsample layers serve the same purpose — generating image features. The final step is to classify the input image based on the detected features. In CNN, this is done by dense layers on top of the net. This part of the network is called the classification . It may contain several layers on top of each other with full connectivity, but usually ends with a layer of softmax class activated by a multi-variable logistic activation function in which the number of blocks equals the number of classes. At the output of this layer is the probability distribution of classes for the input object. Now the image can be classified by selecting the most likely class.

Common approach: no deep learning
The term "image processing" refers to a wide class of tasks, the input data for which are images, and the output can be both images and sets of associated characteristics. There are many options: classification, segmentation, annotation, object detection, etc. In this article, we explore the classification of images not only because it is the simplest task, but also because it underlies many other tasks.
The general approach to the problem of image classification consists of the following two steps:
- Generation of significant features of the image.
- The classification of the image based on its characteristics.
The generally accepted sequence of operations uses simple models such as multi-level perception (MultiLayer Perceptron, MLP), the Support Vector Machine (SVM), the k-nearest-neighbor method, and logistic regression over hand-created features. Characteristics are generated using various transformations (for example, rendering in shades of gray and defining thresholds) and descriptors, for example, oriented gradient histograms (Histogram of Oriented Gradients, HOG ) or scale-invariant feature transformations ( SIFT ), and etc.
The main limitation of the generally accepted methods is the participation of an expert who chooses a set and sequence of steps for generating features.
Over time, it was noticed that most of the feature generation techniques can be generalized using kernels (filters) - small matrices (usually 5 × 5), which are convolutions of the original images. Convolution can be viewed as a sequential two-step process:
- Pass the same fixed core throughout the original image.
- At each step, calculate the scalar product of the kernel and the original image at the point of the current location of the kernel.
The result of the convolution of the image and the kernel is called the feature map.
A more rigorous explanation is given in the corresponding chapter of the recently published book Deep Learning, by I. Goodfellow, I. Bengio, and A. Courville.

The process of core convolution (dark green) with the original image (green), which results in a feature map (yellow).
A simple example of a transformation that can be performed using filters is image blurring. Take a filter consisting of all units. It calculates the average value of the neighborhood defined by the filter. In this case, the neighborhood is a square section, but it can be cruciform or anything else. Averaging leads to loss of information about the exact position of objects, thus blurring the entire image. A similar intuitive explanation can be given for any manually created filter.

The result of the convolution of the image of the Harvard University building with three different cores.
Convolutional neural networks
The convolutional approach to the classification of images has several significant drawbacks:
- Multistep process instead of through sequence.
- Filters are an excellent generalization tool, but they are fixed matrices. How to choose weights in the filters?
Fortunately, learner filters were invented, which are the basic principle behind CNN. The principle is simple: We will train the filters applied to the description of the images in order to best perform their task.
CNN does not have one inventor, but one of the first instances of their use is LeNet-5 * in “Applying Gradient-Based Learning to the Document Recognition Problem” (Gradient-based Learning Applied to Document Recognition) by I. LeKun and others authors.
CNN kill two birds with one stone: there is no need for a preliminary definition of filters, and the learning process becomes transparent. The typical CNN architecture consists of the following parts:
- Convolutional layers
- Subsample layers
- Dense (fully connected) layers
Consider each part in more detail.
Convolutional layers
The convolutional layer is the main structural element of CNN. A convolutional layer has a set of characteristics:
Local (sparse) connectivity . In dense layers, each neuron is connected to each neuron of the previous layer (therefore, they were called dense). In the convolutional layer, each neuron is connected to only a small part of the neurons of the previous layer.

An example of a one-dimensional neural network. (left) Connection of neurons in a typical dense network, (right) Characteristics of local connectivity inherent in the convolutional layer. The images are taken from the book “Deep Learning” (Deep Learning) by I. Goodfellow and other authors. The
size of the area with which the neuron is connected, is called the filter size (filter length in the case of one-dimensional data, for example, time series, or width / height in the case of two-dimensional data, for example, images). In the figure on the right, the filter size is 3. The weights with which the connection is made are called a filter (a vector in the case of one-dimensional data and a matrix for two-dimensional). The pitch is the distance that the filter moves through the data (in the figure on the right, the pitch is 1). The idea of local connectivity is nothing more than a kernel moving a step. Each convolutional level neuron represents and implements one specific position of the nucleus, sliding along the original image.

Two adjacent one-dimensional convolutional layers.
Another important property is the so-calledsusceptibility zone . It reflects the number of positions of the original signal that the current neuron can “see”. For example, the susceptibility zone of the first layer of the network shown in the figure is equal to the size of filter 3, since each neuron is connected to only three neurons of the original signal. However, on the second layer, the susceptibility zone is already equal to 5, since the neuron of the second layer aggregates three neurons of the first layer, each of which has a susceptibility zone 3. With increasing depth, the susceptibility zone grows linearly.
Shared parameters. Recall that in classical image processing, the same core slid across the entire image. Here the same idea applies. We fix only the filter size of the weighting factors for one layer and we will apply these weights to all neurons in the layer. This is equivalent to sliding the same core over the entire image. But the question may arise: how can we learn something with such a small number of parameters?

Dark arrows represent the same weights. (left) Normal MLP, where each weighting factor is a separate parameter, (right) Example of separation of parameters, where several weights indicate the same learning parameter
Spatial structure. The answer to this question is simple: we will train several filters in one layer! They are placed parallel to each other, thus forming a new dimension.
Let's pause for a while and explain the presented idea using the example of a 227 × 227 two-dimensional RGB image. Note that here we are dealing with a three-channel input image, which, in essence, means that we have three input images or three-dimensional input data.

The spatial structure of the input image
We will consider the dimensions of the channels as the depth of the image (note that this is not the same as the depth of the neural networks, which is equal to the number of layers of the network). The question is how to determine the core for this case.

An example of a two-dimensional core, essentially a three-dimensional matrix with an additional depth measurement. This filter gives convolution with the image; that is, it slides across the image in space, calculating scalar products. The
answer is simple, although it is still not obvious: let's make the core also three-dimensional. The first two measurements will remain the same (the width and height of the core), and the third dimension is always equal to the depth of the input data.

An example of spatial convolution step. The result of the scalar product of a filter and a small section of an image of 5 × 5 × 3 (i.e. 5 × 5 × 5 + 1 = 76 dimension of the scalar product + shift) is one number.
In this case, the entire 5 × 5 × 3 section of the original image is transformed one number, and the three-dimensional image itself will be transformed intofeature map ( activation card ). The feature map is a set of neurons, each of which calculates its own function taking into account the two basic principles discussed above: local connectivity (each neuron is associated with only a small part of the input data) and parameter sharing (all neurons use the same filter). Ideally, this feature map will be the same as the one already encountered in the example of the generally accepted network - it stores the results of the convolution of the input image and the filter.

Character map as a result of convolution of the kernel with all spatial positions
Note that the depth of the feature map is 1, since we used only one filter. But nothing prevents us from using more filters; for example, 6. All of them will interact with the same input data and will work independently of each other. Go one step further and combine these feature maps. Their spatial dimensions are the same, since the dimensions of the filters are the same. Thus, the feature maps assembled together can be viewed as a new three-dimensional matrix, the depth dimension of which is represented by feature maps from different nuclei. In this sense, the RGB channels of the input image are nothing more than the three original feature maps.

Parallel application of several filters to the input image and the resulting set of activation cards
Such an understanding of feature maps and their combination is very important, since, having realized this, we can expand the network architecture and install convolutional layers one on top of another, thereby increasing the area of susceptibility and enriching our classifier.

Convolutional layers laid over each other. In each layer, the sizes of filters and their number can vary.
Now we understand what a convolutional network is. The main purpose of these layers is the same as in the conventional approach - to detect significant features of the image. And, if in the first layer these signs can be very simple (the presence of vertical / horizontal lines), with the depth of the network their degree of abstraction increases (the presence of a dog / cat / person).
Subsample layers
Convolutional layers are the main structural element of CNN. But there is another important and often used part - these are the subsample layers. In conventional image processing, there is no direct analogue, but a subsample can be considered as a different type of core. What is it?

Sample subsamples. (left) How subsampling changes spatial (but not channel!) sizes of data arrays, (right) Schematic diagram of subsampling
The subsample filters a portion of the neighborhood of each pixel of the input data with a certain aggregation function, for example, maximum, average, etc. The subsample is essentially the same as convolution, but the pixel combining function is not limited to scalar product. Another important difference is that the subsample works only in the spatial dimension. A characteristic feature of the subsample layer is that the step is usually equal to the size of the filter (the typical value is 2).
The subsample has three main objectives:
- Reduction of spatial dimension, or downsampling. This is done to reduce the number of parameters.
- The growth of the susceptibility zone. At the expense of the neurons of the subsample, more steps of the input signal are accumulated in the subsequent layers.
- Translational invariance to small irregularities in the position of the patterns in the input signal. By calculating the aggregation statistics of small neighborhoods of the input signal, a subsample can ignore small spatial displacements in it.
Tight layers
Convolutional layers and subsample layers serve the same purpose — generating image features. The final step is to classify the input image based on the detected features. In CNN, this is done by dense layers on top of the net. This part of the network is called the classification . It may contain several layers on top of each other with full connectivity, but usually ends with a layer of softmax class activated by a multi-variable logistic activation function in which the number of blocks equals the number of classes. At the output of this layer is the probability distribution of classes for the input object. Now the image can be classified by selecting the most likely class.
