Image Processing Matrix Filters
This article tells not only about the most common image processing filters, but in an understandable form describes the algorithms for their operation. The article is primarily aimed at programmers involved in image processing.
There are many filters using the convolution matrix, the main ones will be described below.
The convolution matrix is a matrix of coefficients that is “multiplied” by the value of the image pixels to obtain the desired result.
Below is the application of the convolution matrix:
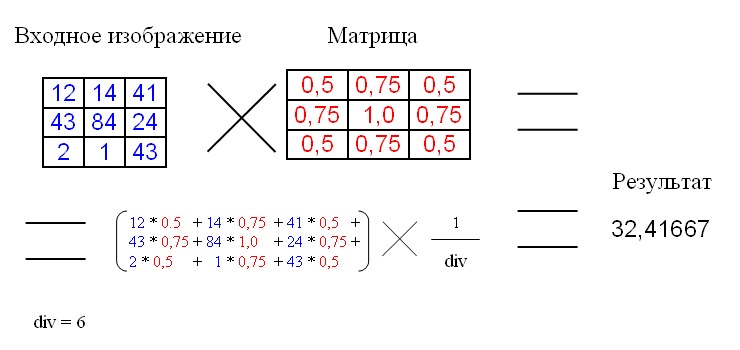
div is the normalization coefficient so that the average intensity remains unchanged.
In the example, the matrix has a size of 3x3, although the size may be larger.
The most commonly used convolution matrix filter is the blur filter.
Usually the matrix is filled in according to the normal (Gaussian law). Below is a 5x5 blur matrix filled in according to the law of the Gaussian distribution.

The coefficients are already normalized, so the div for this matrix is one.
The strength of the blur depends on the size of the matrix.

It is worth mentioning the boundary conditions (this problem is relevant for all matrix filters). The upper left pixel does not have a “neighbor” to the right of it, therefore, we have nothing to multiply the matrix coefficient.

There are 2 solutions to this problem:
1. Applying the filter only to the “window” of the image, which has the coordinates of the upper left corner [kernelSize / 2, kernelSize / 2], and for the lower right [width - kernelSize / 2, height - kernelSize / 2]. kernelSize - matrix size; width, height - image size.
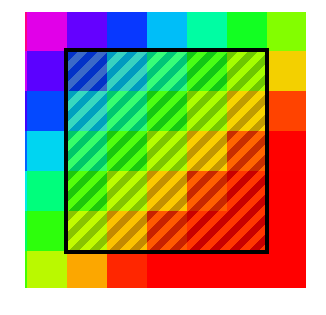
This is not the best way, since the filter does not apply to the whole image. At the same time, quality suffers rather much if the filter size is large.
2. The second method (addition) requires the creation of an intermediate image. The idea is to create a temporary image with dimensions (width + 2 * kernelSize / 2, height + 2 * kernelSize / 2). The input image is copied to the center of the image, and the edges are filled with the extreme pixels of the image. Blur is applied to the intermediate buffer, and then the result is extracted from it.

This method has no drawbacks in quality, but it is necessary to perform unnecessary calculations.
The Gaussian blur filter has complexity O (hi * wi * n * n), where hi, wi are the image sizes, n is the size of the matrix (filter core). This algorithm can be optimized with acceptable quality.
The square core (matrix) can be replaced by two one-dimensional: horizontal and vertical. For a core size of 5, they will look like:

The filter is applied in 2 passes: first horizontal, and then vertical (or per revolution) to the result.
The complexity of this algorithm will be O (hi * wi * n) + O (hi * wi * n) = 2 * O (hi * wi * n), which for a kernel size of more than two is faster than the traditional method with a square matrix.
To improve clarity, you must use the following matrix:
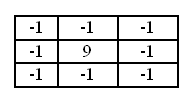
This matrix increases the difference in values at the borders. Div for this matrix is 1.

The GIMP program has a “convolution matrix” filter, which simplifies the search for the matrix transformation you need.
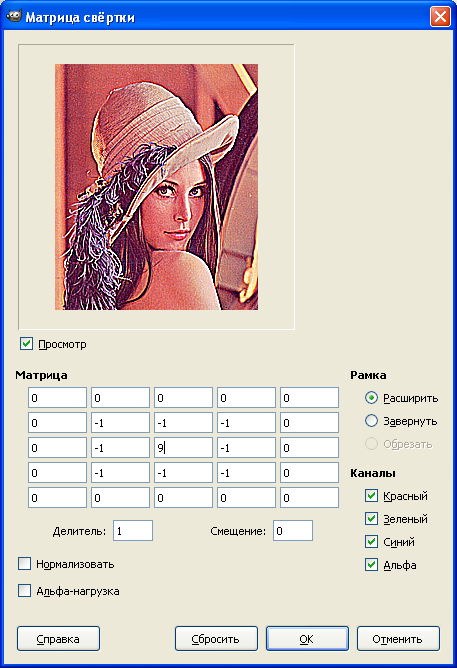
You can find more detailed information about filters based on the convolution matrix in the article “Graphic filters based on the twist matrix” .
A median filter is commonly used to reduce noise or “smooth” an image.

The filter works with matrices of various sizes, but unlike the convolution matrix, the matrix size affects only the number of pixels in question.
The median filter algorithm is as follows:
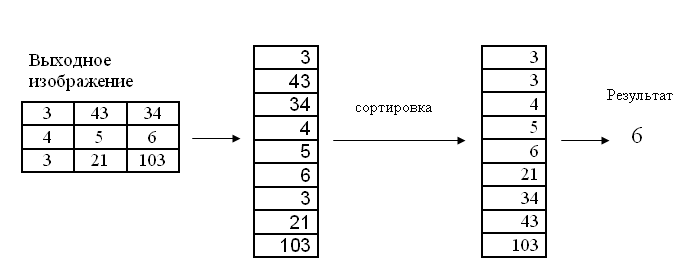
For the current pixel, the pixels that "fall" into the matrix are sorted, and the average value is selected from the sorted array. This value is the output for the current pixel.
Below is the median filter for a core size of three.
Filters build-up and erosion are used to obtain morphological expansion or narrowing, respectively. Simply put, for images, this means choosing a pixel with maximum or minimum intensity from a neighborhood.

As a result of the buildup, there is an increase in bright objects, and erosion - an increase in dark objects.
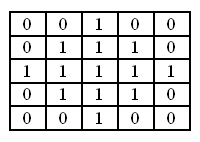
The filter uses an input image and a binary matrix. The binary matrix determines the shape of the neighborhood. Usually the neighborhood has a circular shape.
The build-up filter can be used to increase glare, bright reflections.
The article described some of the image processing filters, described their algorithms and application features.
en.wikipedia.org/wiki/Median_filter
www.mathworks.com/help/toolbox/images/f18-12508.html#f18-20972
en.wikipedia.org/wiki/Mathematical_morphology
habrahabr.ru/post/43895
Convolution matrix
There are many filters using the convolution matrix, the main ones will be described below.
The convolution matrix is a matrix of coefficients that is “multiplied” by the value of the image pixels to obtain the desired result.
Below is the application of the convolution matrix:

div is the normalization coefficient so that the average intensity remains unchanged.
In the example, the matrix has a size of 3x3, although the size may be larger.
Blur filter
The most commonly used convolution matrix filter is the blur filter.
Usually the matrix is filled in according to the normal (Gaussian law). Below is a 5x5 blur matrix filled in according to the law of the Gaussian distribution.

The coefficients are already normalized, so the div for this matrix is one.
The strength of the blur depends on the size of the matrix.

It is worth mentioning the boundary conditions (this problem is relevant for all matrix filters). The upper left pixel does not have a “neighbor” to the right of it, therefore, we have nothing to multiply the matrix coefficient.

There are 2 solutions to this problem:
1. Applying the filter only to the “window” of the image, which has the coordinates of the upper left corner [kernelSize / 2, kernelSize / 2], and for the lower right [width - kernelSize / 2, height - kernelSize / 2]. kernelSize - matrix size; width, height - image size.

This is not the best way, since the filter does not apply to the whole image. At the same time, quality suffers rather much if the filter size is large.
2. The second method (addition) requires the creation of an intermediate image. The idea is to create a temporary image with dimensions (width + 2 * kernelSize / 2, height + 2 * kernelSize / 2). The input image is copied to the center of the image, and the edges are filled with the extreme pixels of the image. Blur is applied to the intermediate buffer, and then the result is extracted from it.

This method has no drawbacks in quality, but it is necessary to perform unnecessary calculations.
The Gaussian blur filter has complexity O (hi * wi * n * n), where hi, wi are the image sizes, n is the size of the matrix (filter core). This algorithm can be optimized with acceptable quality.
The square core (matrix) can be replaced by two one-dimensional: horizontal and vertical. For a core size of 5, they will look like:

The filter is applied in 2 passes: first horizontal, and then vertical (or per revolution) to the result.
The complexity of this algorithm will be O (hi * wi * n) + O (hi * wi * n) = 2 * O (hi * wi * n), which for a kernel size of more than two is faster than the traditional method with a square matrix.
Clarity filter
To improve clarity, you must use the following matrix:

This matrix increases the difference in values at the borders. Div for this matrix is 1.

The GIMP program has a “convolution matrix” filter, which simplifies the search for the matrix transformation you need.

You can find more detailed information about filters based on the convolution matrix in the article “Graphic filters based on the twist matrix” .
Median filter
A median filter is commonly used to reduce noise or “smooth” an image.

The filter works with matrices of various sizes, but unlike the convolution matrix, the matrix size affects only the number of pixels in question.
The median filter algorithm is as follows:
For the current pixel, the pixels that "fall" into the matrix are sorted, and the average value is selected from the sorted array. This value is the output for the current pixel.
Below is the median filter for a core size of three.

Filters erosion and building
Filters build-up and erosion are used to obtain morphological expansion or narrowing, respectively. Simply put, for images, this means choosing a pixel with maximum or minimum intensity from a neighborhood.

As a result of the buildup, there is an increase in bright objects, and erosion - an increase in dark objects.
The filter uses an input image and a binary matrix. The binary matrix determines the shape of the neighborhood. Usually the neighborhood has a circular shape.

The build-up filter can be used to increase glare, bright reflections.
Conclusion
The article described some of the image processing filters, described their algorithms and application features.
en.wikipedia.org/wiki/Median_filter
www.mathworks.com/help/toolbox/images/f18-12508.html#f18-20972
en.wikipedia.org/wiki/Mathematical_morphology
habrahabr.ru/post/43895
