Part number 2. Introduction to folding biology. Mat. the criteria
This is a continuation of the article Part No. 1. Introduction to folding biology. From proteins to RNA . Here we describe mathematically the covalent and hydrogen bonds. Let's see what angles we will rotate at the RNA for folding. And let's touch on the question “what’s the difficulty?”
First two slides:
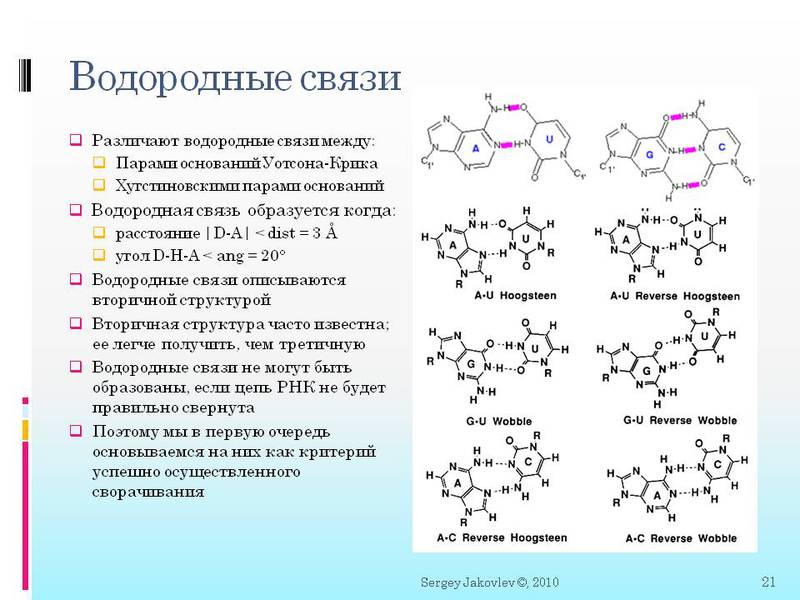

here you see a more rigorous definition of covalent and hydrogen bonds. And then how they are described mathematically. Further it will be important for us:
1. To calculate whether forbidden covalent bonds appeared longer than to make the actual rotation and to calculate a dozen hydrogen bonds. Therefore, this is done only when, according to all other criteria, we are satisfied with the found state. Consider that there is simply a GetFullCovalentBond () function that tells us if there is at least one forbidden covalent bond. If there is, we’ll go ahead and take these states into account. Although, comparatively, in the FoldIt game, collisions are calculated quickly enough and get rid of these states from “bad” states. This makes some sense. But alas, I do not have an algorithm how to do this normally, so far without it.
2. It is important that between the molecules formed immediately or two or three (depending on type) hydrogen bonds. Further we will speak in the context of “a hydrogen bond has formed between nucleotides” - means that all two / three bonds have formed.
3. At first, I was very bothered that there could be non-standard hydrogen bonds. Those. not like in DNA only G with C and A with T (but in RNA with U). There may be different surprises. For example, G c U, as well as triple bonds A c two U simultaneously.
4. I will say it again, since this is important - a hydrogen bond is formed when certain atoms are located at a distance of <3 angstroms from each other and at a certain angle <20 degrees. All atom coordinates are calculated in angstroms. And there is a ScoreGroup function (int N1, int N2), where two numbers of nucleotides (molecules) are fed into the chain, and we get an answer to how close they are to create all the necessary hydrogen bonds. The important thing here is that the answer is not just yes / no, but as a function of approaching yes. What kind of function will be discussed in subsequent articles.
Now how can we rotate the chain. Let's start with rotations of only one nucleotide:

The chain rotates only by turning 9 torsion angles. She cannot move in any other way - it is forbidden by biology (energy). 6 angles are located in the so-called main chain, which is shown by the solid line in the figures in the last article. They are marked with Greek letters starting with alpha. Three more angles in the side chain are highly dependent on each other, i.e. you cannot rotate them independently - therefore, we will call this angle with number 7 below - but in reality there will be a combination of three angles. The side chain is a radical, i.e. what the nucleotides a, u, c, g actually differ - and the main chain (12 atoms from 28-33) is the same.
If we have only one nucleotide, it is clear that at 6 angles you can rotate almost without prohibition. And on 7th very few prohibitions. Nothing interferes. If there is already a chain of 2 nucleotides, then prohibitions appear - the atoms of one nucleotide can jump onto the atoms of another. But since the bundle is not large (take the beads - the two balls next to each other are not strong, they may collide with themselves during rotation - the length of the rope is small between them) - there are not many prohibitions either. But if you take 6 or more prohibitions, there can be many.
And here already a turn in one corner by 0.1 degrees can allow them to turn in another angle, for example, to form a hydrogen bond, and without this it will not work.
What is the difficulty?It’s possible to calculate all combinations for a day only for a chain of 2-3 nucleotides, for 4 a week or a month is needed, and then years :)
But not all angles are correlated with each other. There are those that have little effect on each other. But no one knows what it is in this case.
But it’s impossible to take and set the necessary angles in a step, so I want to develop an iterative procedure in order to get the best and best state step by step. But I did such an experiment. Took only 3 nucleotides (biologically degenerate state). And he made turns at the beginning of the first nucleotide, found the best state, then we fix the best of the second, then the third (one iteration - a miscalculation of say 1500 + 1500 + 1500 turns) we fix the best ... and further and further. The algorithm eventually finds this state with a score of -9.41.
If you do this, turn the first nucleotide by 1,500 turns, then for each of the 1,500 options, turn the second by 1,500, then for the combination of the first and second (1,500 * 1,500 options), turn the third by 1,500 turn options. We will get a really exhaustive search of about 3 billion options, and we will get the best condition -13.87.
But the path of exhaustive search is closed, and I would like to reduce it to the local approximation option (the first option). How to do this we will talk in the next part.
For an in-depth understanding, I will give two links:
1. On the details of the experiment described above
2. On the freedom of nucleotide vibrations in the RNA helix , it is clearly seen that the laws are maximally non-linear and there is no simple logic.
First two slides:


here you see a more rigorous definition of covalent and hydrogen bonds. And then how they are described mathematically. Further it will be important for us:
1. To calculate whether forbidden covalent bonds appeared longer than to make the actual rotation and to calculate a dozen hydrogen bonds. Therefore, this is done only when, according to all other criteria, we are satisfied with the found state. Consider that there is simply a GetFullCovalentBond () function that tells us if there is at least one forbidden covalent bond. If there is, we’ll go ahead and take these states into account. Although, comparatively, in the FoldIt game, collisions are calculated quickly enough and get rid of these states from “bad” states. This makes some sense. But alas, I do not have an algorithm how to do this normally, so far without it.
2. It is important that between the molecules formed immediately or two or three (depending on type) hydrogen bonds. Further we will speak in the context of “a hydrogen bond has formed between nucleotides” - means that all two / three bonds have formed.
3. At first, I was very bothered that there could be non-standard hydrogen bonds. Those. not like in DNA only G with C and A with T (but in RNA with U). There may be different surprises. For example, G c U, as well as triple bonds A c two U simultaneously.
4. I will say it again, since this is important - a hydrogen bond is formed when certain atoms are located at a distance of <3 angstroms from each other and at a certain angle <20 degrees. All atom coordinates are calculated in angstroms. And there is a ScoreGroup function (int N1, int N2), where two numbers of nucleotides (molecules) are fed into the chain, and we get an answer to how close they are to create all the necessary hydrogen bonds. The important thing here is that the answer is not just yes / no, but as a function of approaching yes. What kind of function will be discussed in subsequent articles.
Now how can we rotate the chain. Let's start with rotations of only one nucleotide:

The chain rotates only by turning 9 torsion angles. She cannot move in any other way - it is forbidden by biology (energy). 6 angles are located in the so-called main chain, which is shown by the solid line in the figures in the last article. They are marked with Greek letters starting with alpha. Three more angles in the side chain are highly dependent on each other, i.e. you cannot rotate them independently - therefore, we will call this angle with number 7 below - but in reality there will be a combination of three angles. The side chain is a radical, i.e. what the nucleotides a, u, c, g actually differ - and the main chain (12 atoms from 28-33) is the same.
If we have only one nucleotide, it is clear that at 6 angles you can rotate almost without prohibition. And on 7th very few prohibitions. Nothing interferes. If there is already a chain of 2 nucleotides, then prohibitions appear - the atoms of one nucleotide can jump onto the atoms of another. But since the bundle is not large (take the beads - the two balls next to each other are not strong, they may collide with themselves during rotation - the length of the rope is small between them) - there are not many prohibitions either. But if you take 6 or more prohibitions, there can be many.
And here already a turn in one corner by 0.1 degrees can allow them to turn in another angle, for example, to form a hydrogen bond, and without this it will not work.
What is the difficulty?It’s possible to calculate all combinations for a day only for a chain of 2-3 nucleotides, for 4 a week or a month is needed, and then years :)
But not all angles are correlated with each other. There are those that have little effect on each other. But no one knows what it is in this case.
But it’s impossible to take and set the necessary angles in a step, so I want to develop an iterative procedure in order to get the best and best state step by step. But I did such an experiment. Took only 3 nucleotides (biologically degenerate state). And he made turns at the beginning of the first nucleotide, found the best state, then we fix the best of the second, then the third (one iteration - a miscalculation of say 1500 + 1500 + 1500 turns) we fix the best ... and further and further. The algorithm eventually finds this state with a score of -9.41.
If you do this, turn the first nucleotide by 1,500 turns, then for each of the 1,500 options, turn the second by 1,500, then for the combination of the first and second (1,500 * 1,500 options), turn the third by 1,500 turn options. We will get a really exhaustive search of about 3 billion options, and we will get the best condition -13.87.
But the path of exhaustive search is closed, and I would like to reduce it to the local approximation option (the first option). How to do this we will talk in the next part.
For an in-depth understanding, I will give two links:
1. On the details of the experiment described above
2. On the freedom of nucleotide vibrations in the RNA helix , it is clearly seen that the laws are maximally non-linear and there is no simple logic.
