Sharding in Blockchain

Hello everyone, I am one of the developers of Near Protocol, which, among other things, implements sharding, and in this article I want to tell you in detail what sharding in general is in the blockchain, how it works, and touch on a number of problems that arise when trying to build it.

It is well known that Ethereum, the most popular dApps platform, handles less than 20 transactions per second. Because of this restriction, the transaction price and the time for their confirmation is very high: despite the fact that the block in Ethereum is published every 10-12 seconds, according to ETH Gas Station, the time between sending a transaction and how it actually falls into the block is on average 1.2 minutes The low bandwidth, high prices and long transaction confirmations prevent the launch of any high-performance services on Ethereum.

The main reason Ethereum cannot process more than 20 transactions per second is that every node in Ethereum must check every transaction. In the five years since the release of Ethereum, many ideas have been proposed on how to solve this problem. These solutions can be roughly divided into two groups: those that offer to delegate the execution of transactions to a small group of nodes with very good hardware, and those that offer each node to process only a subset of all transactions. An example of the first approach is Thunder , in which blocks are created by only one node, which, according to the developers, allows receiving 1200 transactions per second, which is 100 times more than Ethereum. Other examples from the first category are Algorand , SpaceMesh ,Solana . All these protocols improve various aspects of the protocol and allow you to perform more transactions than in Ethereum, but all are limited by the speed of one (albeit very powerful) machine.

The second approach, in which each node processes only a subset of transactions, is called Sharding. This is how the Ethereum Foundation plans to increase the throughput of Ethereum.

In this post, I will tell you how the Sharding works in Blockchain using the example of several protocols that are currently under development.

The easiest Sharding

In the simplest implementation, instead of supporting one blockchain, we will support several, and call each such blockchain “shard”. Each shard is supported by an independent set of nodes that verify transactions and create blocks. Hereinafter I will call such nodes validators.

Each shard is responsible for some subset of contracts and accounts. Suppose for now that transactions always operate only with contracts and accounts within a single shard. Such a simplified design is enough to show some interesting problems and features of sharding.

Purpose of validators and central blockchain

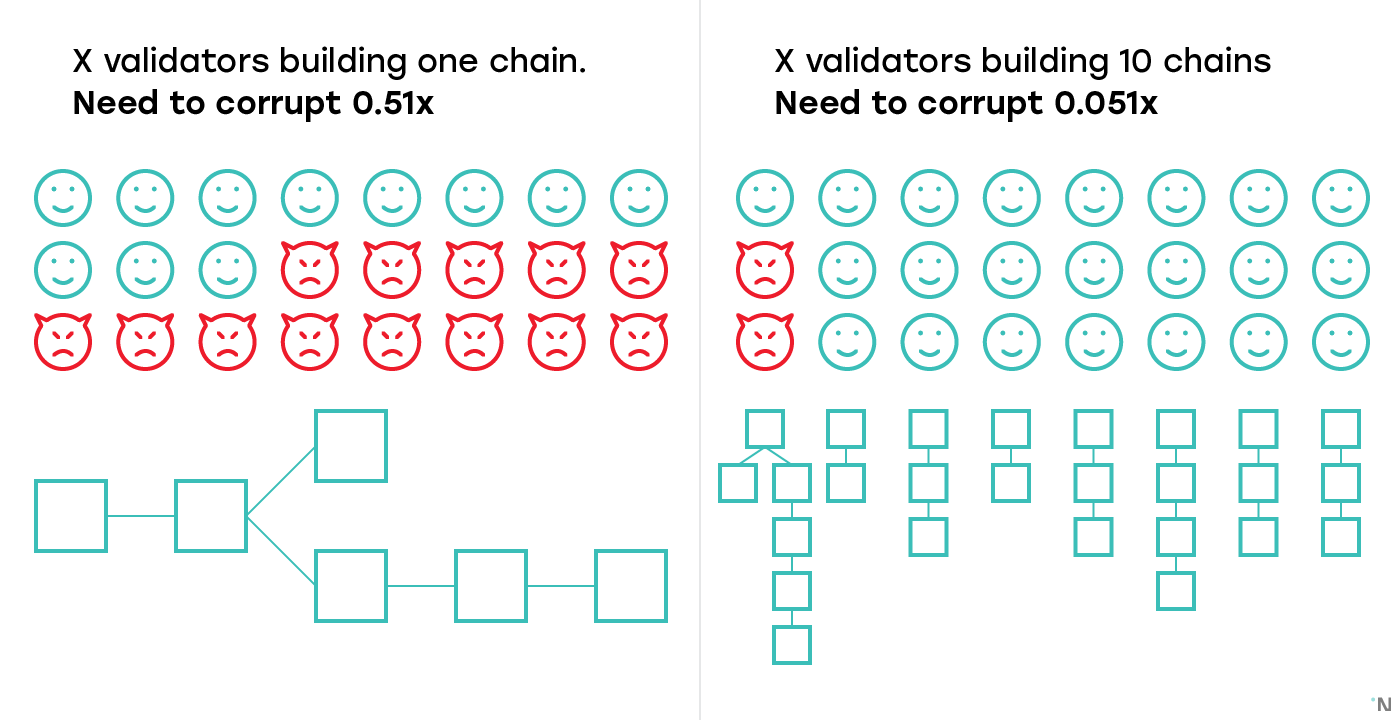
The first problem with the fact that each shard has its own validators is that if we have 10 shadrov, then every shard is now 10 times less reliable than one blockchain would be. So, if a blockchain with X validators decides to make hard forks into a shardirovannuyu system with 10 shards, and breaks X validators between 10 shards, in each shard now only X / 10 validators, and gaining control over the shard requires gaining control over 5.1% (51 % / 10) validators.

Which leads to the first interesting question: who assigns validators to shards? Having control over 5.1% of validators is a problem only if all 5.1% of validators are in one shard. If the validators cannot choose which shard they are assigned to themselves, gaining control over 5.1% of the validators before they are assigned to shards will not allow one to gain control over any shard.

Almost all existing proposed sharding designs use some source of random numbers to assign validators to shards. Obtaining random numbers in a distributed system in which participants do not trust each other is in itself not fully solved a problem today, which we will not touch on in this article, and just assume that we have such a source of random numbers.

Both obtaining random numbers and assigning validators are calculations on a system-wide scale, not specific to any particular shard. For such computations, there is an additional dedicated blockchain in modern designs of shardy blockchains, which exists solely to perform computations on a system scale. In addition to random numbers and the assignment of validators, such calculations can be the hashes of the last blocks from shards and their preservation; processing of pledges in the Proof-of-Stake systems, and the study of evidence of incorrect behavior with the concomitant selection of such pledges; rebalancing shards, if such a function is provided. Such a blockchain is called the Beacon chain in Ethereum 2.0 and Near Protocol, the Relay chain in PolkaDot, and the Cosmos Hub in Cosmos.

In this post we will call such a blockchain “central blockchain”. The existence of a central blockchain leads us to the next interesting topic - quadratic sharding.

Quadratic sharding

Sharding is often presented as a solution that infinitely scales with an increase in the number of nodes. Probably, you can really create a system with this property, but systems with a central blockchain have a top limit on the number of shards, and as a result do not have infinite scalability. It is easy to understand why: the central blockchain performs some calculations, such as assigning validators and storing the latest states of the shard, whose complexity is proportional to the number of the shard. Since the central blockchain itself is not shaded, and its bandwidth is limited by the bandwidth of each node, the number of shards that it can support is limited.

Let's see how the throughput of the entire system will change if the power of the nodes supporting it increases by a factor of k. Each shard will be able to process k times more transactions, and the central blockchain will be able to support k times the shard. Thus, the bandwidth of the entire system will increase k ^ 2 times. Hence the name “quadratic sharding” (quadratic sharding).

It is difficult to predict how much the shard can support the central blockchain today, but most likely in the near future we will not come close to the transaction limit for the sharding blockchain with quadratic sharding. Most likely, we have previously rested in the limit of how many nodes are needed to support such a number of shards.

State sharding

Condition is all information about all accounts and contracts. So far we have talked about sharding in general, without specifying exactly what is being shaded. Nodes in the blockchain perform the following three tasks: 1) perform transactions 2) send transactions and blocks to other nodes and 3) store the state and history of the blockchain. Each of these three tasks involves a constantly growing load on nodes:

1. The need to perform transactions requires more computing power with an increase in the number of transactions;
2. The need to forward transactions requires more network bandwidth as transactions grow;
3. The need to maintain state and history requires more disk space with an increase in the size of the state and / or history. It is important to note that, unlike the first two points, the amount of disk space required grows even if the number of transactions per unit of time does not change.

From the list above it may seem that disk space is the biggest problem, since only disk space grows even if the number of transactions is not growing, but in practice this is not the case. Today, the state of Ethereum takes about 100GB, which can easily be saved on any modern machine, but the number of transactions that Ethereum can process is limited to several tens per second, resting on the computing power and network.

Zilliqa is the most famous project that shorts off calculations and the network but not the state. Sharding computing is easier than sharding a state, because all the nodes have all the state, and can still easily execute contracts that cause other contracts, or affect accounts on different shards. In these aspects, the design of Zilliqa'and too simplified, the criticism of the design in English can be read here .

While sharding state without sharding calculations was proposed, I do not know any projects that actually do this, so we will assume that sharding the state implies sharding calculations.

In practice, the fact that the state is shardy to some extent isolates the shards, allowing them to be independent blockchains, as we defined them above. Validators in shards save only the state specific to their shard, and execute and send only transactions that affect this state. This reduces the load on the processor, disk and network linearly with the number of shards, but brings new problems, such as inter-shard transactions.

Inter-shard transactions

So far, we have seen shards as independent blockchains in terms of how they perform transactions. With such a design, for example, it is impossible to complete a transaction that transfers money between two accounts on two different shards, or to call a contact on one shard from a contract on another. Both scenarios would like to support.

For simplicity, we will consider only transactions that transfer money, and we will assume that each participant has an account on exactly one shard. If a participant on a shard wants to transfer money to a participant on the same shard, the validators of that shard can process this transaction and apply it to the state. But if, for example, Alice has an account on shard # 1 and she wants to send money to Bob with an account on shard # 2, neither validators of shard # 1 (who can’t add money to Bob) nor validators of shard # 2 (who can’t take Alice’s money ) can not complete the transaction and update the status.

There are two large groups of approaches to solving this problem:

1. Synchronous : for any transaction involving multiple shards, the blocks in shards containing the status update for this transaction are performed simultaneously, and the validators in these shards work together to create such blocks. The most elaborate design of this approach, known to me, is Merge Blocks, described (in English) here .

   
   

2. Asynchronous: An inter-shard transaction is performed in shards that it affects, asynchronously: the part of the transaction that adds money to Bob is performed in shard # 2 when the validators in the shard have some proof that the part of the transaction that deducts money from Alice was performed in shard #one. This approach is more popular in the systems being developed today due to the fact that it does not require additional synchronization between shards for the production of blocks. Such systems today are offered in Cosmos, Ethereum Serenity, Near Protocol, Kadena, and others. The problem with this approach is that if the blocks are made independently, there is a chance that one of the blocks containing the status update for the transaction will not be in the canonical chain in its shard, and thus the transaction will only be partially completed. For example, consider the figure below. It shows two shards in which the forks occurred, and an inter-shard transaction, the state update for which is reflected in blocks A and X ', respectively. If the chains AB and V'-X'-Y'-Z 'turn out to be canonical in their shards, then the transaction is completely finalized. If the chains A'-B'-C'-D 'and VX are canonical, then the transaction is completely canceled, which is acceptable. But if, for example, AB and VX become canonical, then one part of the transaction is finalized, and the other is canceled, and the transaction is partially completed. then the transaction is completely canceled, which is acceptable. But if, for example, AB and VX become canonical, then one part of the transaction is finalized, and the other is canceled, and the transaction is partially completed. then the transaction is completely canceled, which is acceptable. But if, for example, AB and VX become canonical, then one part of the transaction is finalized, and the other is canceled, and the transaction is partially completed.

   
   

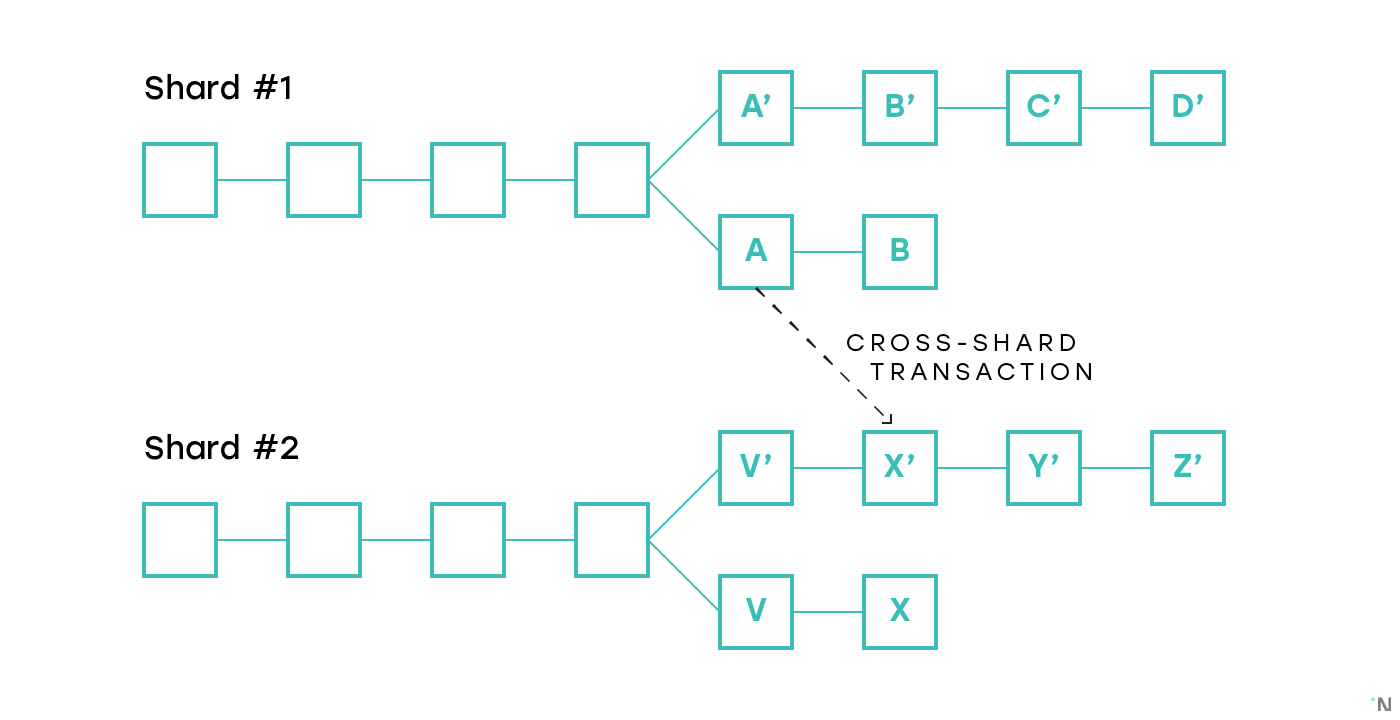
The scenario described above is one of the big problems in sharding, in which all the proposed solutions are not optimal. We will touch it a little lower.

Bad behavior

Now that we’ve figured out how the shaded blockchains work, and studied the concepts of the central blockchain, the assignment of validators and inter-shard transactions, we’ll conclude this article with another interesting topic: what can a participant try to attack the system if he can get control over a sufficiently large number of validators in one shard.

Targeted fork

If the participant has enough control over the shard, he can purposefully create forks. To create forks, it does not matter which consensus is used in shards, in particular, it does not matter whether it is BFT or not, if there are enough validators under the control of the attacker, he can create a fork. For example, the goal of a fork may be to roll back a transaction that paid for something outside the blockchain.

It is argued that getting control over a 50% shard is easier than 50% of the entire network (for example, because a participant may try to hack or bribe validators after they have been assigned to a shard). By definition, inter-shard transactions change state in several shards. Such changes will fall into some blocks in the blockchains of the corresponding shards. It is necessary that either all such blocks be finalized (that is, belonged to the canonical chain in the corresponding shards), or all were not finalized (that is, did not belong to the canonical chains in their shards). Since we assume that some participants with bad intentions, in principle, can gain control over the shard, we cannot believe that forks will not occur, even if Byzantine consensus was reached,

This problem has many solutions, the simplest of which is sometimes to save the hash of the last block in the shard to the central blockchain. The algorithm for choosing a canonical chain in shards then changes so that no target that contains the last block stored on the central blockchain can be canonical. Then, in order to completely avoid situations when a transaction is performed partly due to the fact that some of the blocks containing its state update are outside the canonical chains, you can change the algorithm for performing inter-shard transactions so that shard A does not accept proof of the completion of the transaction in shard B while the block that contains a status update for a transaction in shard B was not saved in the central blockchain.

Creating invalid blocks

If the participant was able to gain control over a sufficiently large number of validators in the shard, he may try to create a completely invalid block. For example, even if the state before the block was such that Alice had 10 tokens, and in Bob it was 0, the block contains only one transaction that sends 10 tokens from Alice’s account to Bob’s account, but in the new state it reflects 0 Alice’s tokens, and 1000 at Bob's

In the classic, not shardirovannogo blockchain, the creation of such a block is impossible, because all the participants, both those who create the blocks and those who simply use the blockchain, check all the blocks, and immediately discard any block that contains such errors. Even if validators controlled by an attacker can build a chain faster, it will not allow them to pass a longer chain containing an invalid block as canonical, because all participants in the network will immediately discard the invalid block and any block that was built on top. Honest validators will continue to build on top of the last valid block, and all participants in the network will see their chain as canonical.

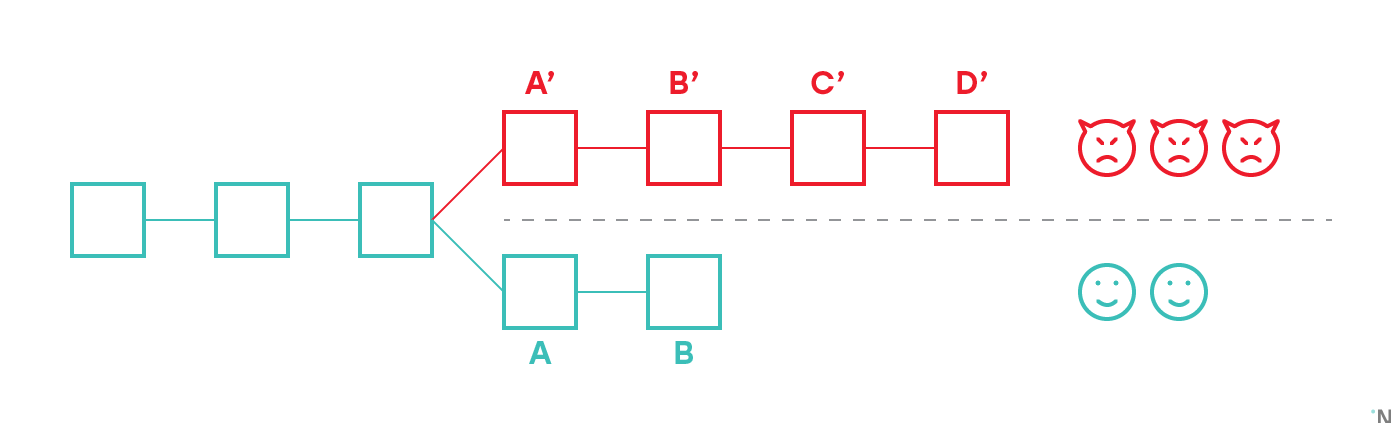
In the figure above, there are five validators, three of which are under the control of the attacker. They created an invalid block A ', and then continued to build a chain on top. Two private validators immediately dropped block A 'as invalid and continued to build on top of the last valid block known to them, thereby creating fork. Since there are fewer validators in an honest chain than in a dishonest one, their chain is shorter. However, in the classic uncharding blockchain, all participants in the system validate all the blocks that they see. Thus, any participant using the blockchain will see that A 'is invalid, discard it, and therefore discard B', C 'and D' as being built on top of an invalid block, and thus all participants will see AB as a canonical chain.

In the shardirovannogo design, no one participant can validate all the blocks in all blockchains. Therefore, we need some kind of mechanism that will allow validators in a particular shard to be sure that at no point in time in the past an invalid block was created in another shard from which they received an inter-shard transaction.

Unlike targeted forks, sending a hash of blocks to the central blockchain does not help, because the central blockchain also does not have the resources to validate all blocks in all shards. The central blockchain can only validate that a sufficient number of validators assigned to the shard have signed the block (and as a result have declared the block is correct).

I know two solutions to the problem, none of which seems satisfactory:

1. To have some kind of mechanism that will allow the system to quickly notice the appearance of forks and invalid blocks. If the Byzantine consensus is used, to create an invalid block, it is necessary that more than 2/3 of the validators belong to the attacker or are compromised by him. If the system is built with the assumption that this can happen, but that at least one honest validator is always there, then a protocol is needed that will allow such an honest validator to find out that an invalid block has been created and notify the system. Since such an honest validator needs time to notice the appearance of a block, check it, prepare a transaction with proof of invalidity, such a protocol requires that other shards and the central blockchain wait for a long enough time after receiving the block before performing any action depending on it.
2. To use some kind of cryptographic mechanism that proves that the entire chain of blocks, including the block containing the transaction and the transaction itself, is valid. Such a mechanism exists, it is called zk-SNARKs (although the part about zk, or zero-knowledge, is not really needed, today there is almost no research in the field of non-zk SNARKs). Unfortunately, today zk-SNARKs are terribly slow, and existing practical implementations work only for a subset of possible calculations.

Many of the protocols that are being developed today are built with the assumption that if the validators are often redistributed, then using the Byzantine consensus the problems described above do not exist. Why it is not so - the topic of a separate article.

I write a lot about blockchain and sharding in English. We also occasionally interview authors of other protocols, such as Cosmos and Solana, digging deep into technical details. If you are interested in the topic, you can follow the new publications and videos by subscribing to my Twitter @AlexSkidanov .