December 2, 2011 at 15:29Decreased exponent of matrix multiplication
News from the world of science: size matrices 
can now multiply by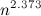 
. In other words, it is proved that 
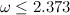, where 
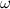is the exponent of matrix multiplication . It was recently proved by Virginia Vasilevska-Williams , thereby improving the estimate 
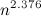received by Coppersmith and Grapes in 1987. I will write about the importance of this algorithm quite a bit. Those who are interested in learning more are invited to read the posts of Scott Aaronson , Richard Lipton and Bill Gasarsch .
So, many theoretical upper bounds for the running time of algorithms use the matrix multiplication exponent. In particular, many graph algorithms exploit this idea: if A is the graph adjacency matrix, then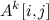
is the number (not necessarily simple!) Of paths of length k between the vertices i and j. This simple idea allows you to 
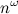check in time whether there is a triangle in the graph (3-clicks): you need to construct the adjacency matrix into a cube (this will require two matrix multiplications) and look at the diagonal. Note that we are talking about theoretical estimates here, since advanced matrix multiplication algorithms even outperform the asymptotically simple cubic algorithm, but in practice they only provide acceleration on huge matrix sizes.
A few more examples:
can now multiply by 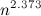. In other words, it is proved that 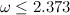, where 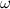is the exponent of matrix multiplication . It was recently proved by Virginia Vasilevska-Williams , thereby improving the estimate 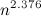received by Coppersmith and Grapes in 1987. I will write about the importance of this algorithm quite a bit. Those who are interested in learning more are invited to read the posts of Scott Aaronson , Richard Lipton and Bill Gasarsch .So, many theoretical upper bounds for the running time of algorithms use the matrix multiplication exponent. In particular, many graph algorithms exploit this idea: if A is the graph adjacency matrix, then
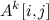is the number (not necessarily simple!) Of paths of length k between the vertices i and j. This simple idea allows you to 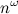check in time whether there is a triangle in the graph (3-clicks): you need to construct the adjacency matrix into a cube (this will require two matrix multiplications) and look at the diagonal. Note that we are talking about theoretical estimates here, since advanced matrix multiplication algorithms even outperform the asymptotically simple cubic algorithm, but in practice they only provide acceleration on huge matrix sizes. A few more examples:
- Distances between all pairs of vertices (all-pairs shortest path).
The shortest paths between all pairs of vertices in an unweighted graph can be found in time
. To do this, we raise the adjacency matrix to the power n (hence, o (1) creeps out to the power), simultaneously calculating the shortest paths. Find out the details, as well as many other similar elegant algorithms, from the
excellent presentation of Uri Zwick. - Maximum 2-feasibility problem (MAX-2-SAT).
The only known algorithm for this task, which works faster than exhaustive search (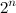
), is also based on matrix multiplication. Its runtime is equal 
and it uses exponential memory. In a nutshell, the idea is this: according to the input formula, we construct a huge graph (at the 
vertices) and with the help of quick matrix multiplication we check whether there is a triangle in it. It is noteworthy that he invented his husband Virginia - Ryan Williams. - Hamiltonian Way (Hamiltonian cycle).
There is still such a funny example in which it is not so important how much we can multiply matrices, but still. An algorithm for finding the Hamiltonian path in time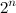and polynomial memory (note that the famous Held-Karp algorithm for this problem is based on dynamic programming and requires exponential memory): it calculates the number of paths of length n-1 on all subsets of graph vertices using the trick indicated above ; after this, the inclusion-exclusion formula allows you to sum the numbers found so that only the number of simple paths of length n-1 remains (and this is the Hamiltonian path).