August 11, 2011 at 11:15Creating a binary tree
- Transfer
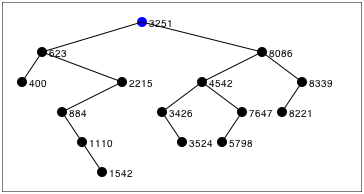When I started learning ruby, I decided to implement a binary tree and some of its basic operations (insert, delete, walk, and search), in order to better understand the language. Binary trees, this is a good exercise to understand the features of the language, such as: conditional operators, loops, classes. At the same time, this is an opportunity to solve an interesting problem. The binary tree algorithm is well described in many books and on the Internet. To complicate the task, I also implemented the rendering of the binary tree using html5 and Canvas. This allows you to more clearly understand the operation of the binary tree. You can watch the demo on the website .
Next, I will briefly describe the implementation of the basic methods of building a binary tree.
Binary tree or binary search tree
The actual code below implements the Binary Search Tree (BST), which is a more specific version of binary trees. In a binary tree, each node has no more than 2 children, one of them is called the "left subtree", and the other is the "right subtree", there is no sorting. In the binary search tree, all nodes are stored in the order reflected in the following rule:
Suppose x is a node in the binary search tree, if y is the "left subtree" for x, then y.key ≤ x.key. If y is the "right subtree" for x, then y.key ≥ x.key.
Implementing a binary search tree
The class for working with the tree that I implemented can be used as follows:
require "binarytree"
tree = BinaryTree.new(40)
tree.add(30)
tree.add(100)
tree.add(20)
tree.add(35)
tree.add(25)
tree.add(34)
puts "Tree nodes: #{tree.to_s}" => "20, 25, 30, 34, 35, 40, 100"We can use this class with numbers, strings, or any native ruby types that support matching (i.e., <=>)
Adding nodes in a binary tree
The code for adding nodes in the binary tree is shown below. This code first checks to see if we already have a root node, if not, then create a root node with a new value. If we already have a root node, we scan the tree nodes (using the rule specified above) until we reach the final node. As soon as we reach the final node we update it to point to a new node.
def add(new_value)
if @root == nil
@root = Node.new(new_value)
@total_nodes = 1
return
end
current = @root
while(true)
if new_value >= current.value
if current.right == nil
current.right = Node.new(new_value)
break
else
current = current.right
end
else
if current.left == nil
current.left = Node.new(new_value)
break
else
current = current.left
end
end
end
@total_nodes += 1
end
Wood walking
One of the advantages of the binary search tree is that it is very easy to get the values stored in it. This process is called "walking on a sorted tree." For example, if we have a tree with the following values: 100, 50, 200, and 150, then the sorted tree will give us the values: 50, 100, 150, and 200. Walking in a tree can be implemented using a recursive function. However, the recursive method, although elegant, is not very effective if the tree is large. The code I implemented does not use recursion, but instead uses an array as a stack to track the nodes it visits. This solution is not as elegant as recursion, but it works well even if there are thousands of nodes in the tree.
def walk
return nil if @root == nil
node = @root
stack = []
ignore_left = false
while(true)
#p "processing #{node.value.to_s}"
if ignore_left
#p "ignoring nodes to the left"
ignore_left = false
else
if node.left != nil
#p "moving to the left"
stack << node
node = node.left
next
end
end
yield node
if node.right != nil
#p "moving to the right"
node = node.right
next
end
break if stack.length == 0
#p "popping from the stack"
node = stack.pop
ignore_left = true
end
end
While I was implementing this method, I realized the beauty and simplicity of one of the best ruby features: blocks. When the algorithm finds the next node to process, it simply gives it to the calling program. This allows you to walk on a tree and be completely independent of the actions that we want to perform on each node. For example, you can make the following code for each node:
tree.walk { |node| puts "#{node.value}" }
In this example, the block simply “displays” the values, but we will see a more complex example when we consider the code for rendering a binary tree.
How to draw a binary tree
The binary tree rendering algorithm is very similar to the tree walking algorithm with the exception that we need to calculate the coordinates where each node should be located and how we intersect the nodes. The calculation of coordinates turned out to be an interesting task.
The main algorithm is as follows:
- Draw the root node with the given coordinates
- Draw the left subtree from the left of the root node
- Draw the right subtree to the right of the root node
def draw_node(root, x, y, block)
return if root == nil
block.call(root, x, y, x, y)
draw_left(root.left, x, y, block) if root.left != nil
draw_right(root.right, x, y, block) if root.right != nil
end
To calculate the coordinates of the left subtree, we calculate how many children are on the right side of the left subtree. The resulting number, we use for negative displacement along the x axis. Further we recursively call this method for the left and right subtree.
def draw_left(node, parent_x, parent_y, block)
if node.right != nil
count = 1 + children_count(node.right)
else
count = 0
end
x = parent_x - @x_distance - (count*@x_distance)
y = parent_y + @y_distance
block.call(node.value, x, y, parent_x, parent_y)
draw_left(node.left, x, y, block) if node.left != nil
draw_right(node.right, x, y, block) if node.right != nil
end
For the right subtree, do the same thing, but vice versa.
def draw_right(node, parent_x, parent_y, block)
if node.left != nil
count = 1 + children_count(node.left)
else
count = 0
end
x = parent_x + @x_distance + (count*@x_distance)
y = parent_y + @y_distance
block.call(node.value,x,y, parent_x, parent_y)
draw_left(node.left, x, y, block) if node.left != nil
draw_right(node.right, x, y, block) if node.right != nil
end
Like the walk method, the method of rendering in fact does not draw anything, but only indicate the coordinates of the display of the object. The following example shows the construction of a tree with coordinates in the console:
require "binarytree"
require "binarytreedrawer"
tree = BinaryTree.new
tree.add(100)
tree.add(50)
tree.add(150)
tree.add(25)
tree.add(75)
tree.add(125)
tree.add(175)
drawer = BinaryTreeDrawer.new(tree)
drawer.draw(0,0, Proc.new { |value, x, y, px, py|
puts "Value #{value} at (#{x}, #{y})"
})
=> Value 100 at (0, 0)
=> Value 50 at (-40, 30)
=> Value 25 at (-60, 60)
=> Value 75 at (-20, 60)
=> Value 150 at (40, 30)
=> Value 125 at (20, 60)
=> Value 175 at (60, 60)
A real example of rendering a binary tree on a web page
Having coordinates, we can use any graphics program to draw a tree. In this web application I will use HTML 5 Canvas as a surface for drawing, and several JS methods. The following is a simple example of how I generate JS calls to draw a tree:
drawer = BinaryTreeDrawer.new(@tree)
drawer.draw(0, 0, Proc.new { |value, x, y, px, py|
circles << "draw_circle(centerX + #{x}, offsetY + #{y}, 5);"
lines << "draw_line(centerX + #{x}, offsetY + #{y}, centerX + #{px}, offsetY + #{py});"
labels << "draw_label(centerX + 7 + #{x}, offsetY+5+#{y}, \"#{value}\");"
})
Note that this code simply creates three arrays (circles, lines, labels) with calls to JavaScript methods. These arrays are later inserted into a web page and draw a tree on the client side.
Source Code and Demo
If you want to see a demo, you can visit http://binarytree.heroku.com and generate some binary trees with random data or draw a binary tree with your own dataset.
All sources for implementing the binary tree, as well as a demo site, are posted on GitHub .