Data Structures: Binary Heap
The binary heap is a simply implemented data structure that allows you to quickly (in logarithmic time) add elements and retrieve an element with the highest priority (for example, the maximum value).
For further reading, it is necessary to have an idea of trees , and it is also advisable to know about evaluating the complexity of algorithms . The algorithms in this article will be accompanied by C # code.
The binary heap is a complete binary tree for which the main property of the heap is satisfied : the priority of each vertex is greater than the priorities of its descendants. In the simplest case, the priority of each vertex can be considered equal to its value. In this case, the structure is called max-heap , since the root of the subtree is the maximum of the values of the elements of the subtree. This article uses just such a representation for simplicity. Let me remind you that a tree is called complete binary if each vertex has no more than two descendants, and the filling of the vertex levels goes from top to bottom (from the same level - from left to right).
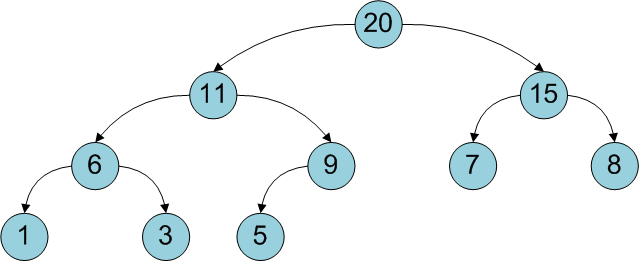
It is convenient to store the binary heap in the form of a one-dimensional array, and the left descendant of the vertex with the index
I will give a class blank in C #:
The new element is added to the last place in the array, that is, the position with the index

It is possible that this will violate the main property of the heap, since the new element may be larger than the parent. In this case, you should “raise” the new element one level (change with the parent vertex) until the heap’s main property is observed:
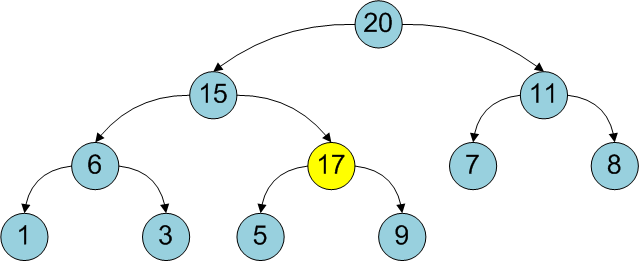

In other words, the new element “pops up”, “pushes” upwards, until it takes its place . The complexity of the algorithm does not exceed the height of the binary heap (since the number of “lifts” is not greater than the height of the tree), that is, it is equal to O (log 2 N).
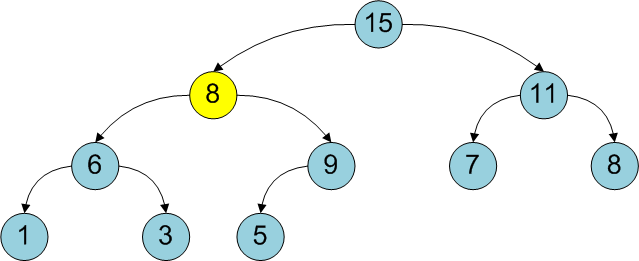
During other operations with an already constructed binary heap, the heap’s main property may also be violated: a vertex may become smaller than its descendant.
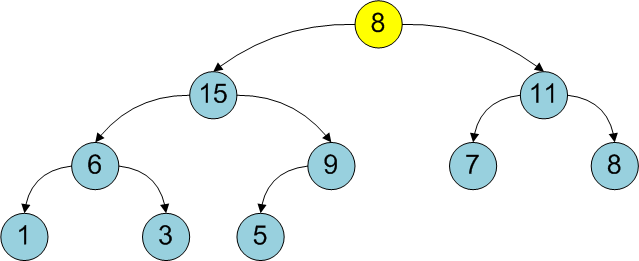
The method
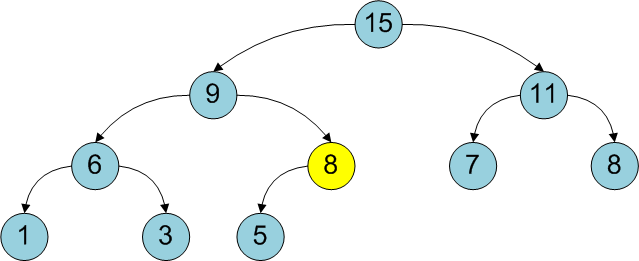
The most obvious way to build a bunch from an unordered array is to add all its elements in turn. The time estimate of such an algorithm is O (N log 2 N). However, you can build a bunch even faster - for O (N). First you need to build a tree from all the elements of the array, not caring about observing the main property of the heap, and then call the method
In an ordered
Note that you can sort the array by first building a binary heap from it, and then sequentially extracting the maximum elements. Let us evaluate the time complexity of such an element: heap construction - O (N),
Thus, the binary heap has a tree structure of a logarithmic height (relative to the number of vertices), allows you to add elements in a logarithmic time and extract an element with maximum priority in constant time. At the same time, the binary heap is easy to implement and does not require additional memory.
For further reading, it is necessary to have an idea of trees , and it is also advisable to know about evaluating the complexity of algorithms . The algorithms in this article will be accompanied by C # code.
Introduction
The binary heap is a complete binary tree for which the main property of the heap is satisfied : the priority of each vertex is greater than the priorities of its descendants. In the simplest case, the priority of each vertex can be considered equal to its value. In this case, the structure is called max-heap , since the root of the subtree is the maximum of the values of the elements of the subtree. This article uses just such a representation for simplicity. Let me remind you that a tree is called complete binary if each vertex has no more than two descendants, and the filling of the vertex levels goes from top to bottom (from the same level - from left to right).

It is convenient to store the binary heap in the form of a one-dimensional array, and the left descendant of the vertex with the index
ihas an index2*i+1, and right 2*i+2. The root of the tree is an element with index 0. The height of the binary heap is equal to the height of the tree, that is, log 2 N, where Nis the number of elements in the array. I will give a class blank in C #:
public class BinaryHeap
{
private List list;
public int heapSize
{
get
{
return this.list.Count();
}
}
}
Add item
The new element is added to the last place in the array, that is, the position with the index
heapSize: 
It is possible that this will violate the main property of the heap, since the new element may be larger than the parent. In this case, you should “raise” the new element one level (change with the parent vertex) until the heap’s main property is observed:


In other words, the new element “pops up”, “pushes” upwards, until it takes its place . The complexity of the algorithm does not exceed the height of the binary heap (since the number of “lifts” is not greater than the height of the tree), that is, it is equal to O (log 2 N).
public void add(int value)
{
list.Add(value);
int i = heapSize - 1;
int parent = (i - 1) / 2;
while (i > 0 && list[parent] < list[i])
{
int temp = list[i];
list[i] = list[parent];
list[parent] = temp;
i = parent;
parent = (i - 1) / 2;
}
}
Binary Heap Ordering
During other operations with an already constructed binary heap, the heap’s main property may also be violated: a vertex may become smaller than its descendant.

The method
heapifyrestores the basic heap property for a tree with a root at the i-th vertex, provided that both subtrees satisfy it. For this, it is necessary to “lower” the i-th vertex (interchange with the largest of the descendants) until the main property is restored (the process ends when there is no descendant, its larger parent). It is easy to see that the complexity of this algorithm is also equal to O (log 2 N).

public void heapify(int i)
{
int leftChild;
int rightChild;
int largestChild;
for (; ; )
{
leftChild = 2 * i + 1;
rightChild = 2 * i + 2;
largestChild = i;
if (leftChild < heapSize && list[leftChild] > list[largestChild])
{
largestChild = leftChild;
}
if (rightChild < heapSize && list[rightChild] > list[largestChild])
{
largestChild = rightChild;
}
if (largestChild == i)
{
break;
}
int temp = list[i];
list[i] = list[largestChild];
list[largestChild] = temp;
i = largestChild;
}
}
Building a binary heap
The most obvious way to build a bunch from an unordered array is to add all its elements in turn. The time estimate of such an algorithm is O (N log 2 N). However, you can build a bunch even faster - for O (N). First you need to build a tree from all the elements of the array, not caring about observing the main property of the heap, and then call the method
heapifyfor all vertices that have at least one descendant (since subtrees that consist of one vertex without descendants are already ordered). The first heapSize/2peaks are guaranteed to have descendants .public void buildHeap(int[] sourceArray)
{
list = sourceArray.ToList();
for (int i = heapSize / 2; i >= 0; i--)
{
heapify(i);
}
}
Extraction (removal) of the maximum element
In an ordered
max-heapmaximum element is always stored in the root. You can restore the order of the binary heap after deleting the maximum element by putting in its place the last element and calling heapifyfor the root, that is, ordering the whole tree.public int getMax()
{
int result = list[0];
list[0] = list[heapSize - 1];
list.RemoveAt(heapSize - 1);
return result;
}
Binary Heap Sort
Note that you can sort the array by first building a binary heap from it, and then sequentially extracting the maximum elements. Let us evaluate the time complexity of such an element: heap construction - O (N),
Nelement extraction - O (N log 2 N). Therefore, the final score is O (N log 2 N). In this case, additional memory for the array is not used.public void heapSort(int[] array)
{
buildHeap(array);
for (int i = array.Length - 1; i >= 0; i--)
{
array[i] = getMax();
heapify(0);
}
}
Conclusion
Thus, the binary heap has a tree structure of a logarithmic height (relative to the number of vertices), allows you to add elements in a logarithmic time and extract an element with maximum priority in constant time. At the same time, the binary heap is easy to implement and does not require additional memory.
