Physicists intend to classify all phases of matter.

Full classification may lead to the emergence of a large number of new materials and technologies. However, the most exotic phases continue to resist the understanding of scientists

Over the last three decades, specialists in the physics of condensed states have discovered a whole wonderful country of new, exotic phases of matter: suddenly emerging collective states of interacting particles, not at all resembling solid, liquid or gaseous states of matter, known to all.

These phases, as some have understood in laboratories, and some on the basis of theoretical calculations, appear when matter cools down almost to absolute zero, which is more than two hundred degrees below freezing point of water under normal conditions. Under these cold conditions, particles can interact in ways that force them to drop all traces of their previous identity. The experiments of the 1980s discovered that in some situations electrons are divided into fractions of particles that can leave traces in the space-time in the form of braids.; in others, massless versions of themselves appear among them. A lattice of rotating atoms becomes a fluid of twisting loops or branching strings; crystals, which did not conduct electricity initially, begin to pass a current across the surface. One of the phases that shocked experts, when her opportunity was first proved mathematically in 2011 , includes very strange entities, " fractons ", interlocking with each other in fractal patterns [according to Wiki, fractons are a fractal analog of phonons , oscillatory motion quanta of atoms crystal / approx. trans.].

Now research teams from Microsoft and other companies are competing to try to write quantum information in braids and loops of some of these phases in order to develop a quantum computer. In the meantime, theorists of condensed matter (CS) physics have recently conducted several studies that are essential for understanding the pattern of collective behavior in order to number and classify all possible phases of matter. If they manage to make a complete classification, it will not only allow describing all the phases of matter in nature seen so far, but also potentially indicate the path to obtaining new materials and technologies.

Researchers under the guidance of dozens of the best theorists and with the help of mathematicians have already classified a whole carriage of phases capable of manifesting in one or twospatial dimensions , associating them with a topology: with mathematics that describes the invariable properties of such forms as a sphere or a torus. They also went deep into the jungle of phases arising in the region of absolute zero in three-dimensional matter.


Xi Chen, a condensed matter theorist from the California Institute of Technology.

Scientists are looking for "not some specific law of physics," said Michael Zalelet[Michael Zaletel], FKS theorist at Princeton University. "They are looking for a space of all possibilities, and this is in some sense a deeper and more beautiful idea." This may be unexpected, but, as Zalelet says, the space of all consistent phases is itself a mathematical object “with an incredibly rich structure, which, as we believe, in one-dimensional and two-dimensional world, one in one, will coincide with these beautiful topological structures” .

There is an “economy of options” on the landscape of all phases, “said Ashwin Vishwanath[Ashvin Vishwanath] from Havrvard University. “And all this seems knowable” - such luck puzzles him. The numbering of the phases of matter could be something "like stamp collecting," said Vishwanath, "each a little different from the others, and there is no connection between them." Instead, the phase classification is more like a “periodic table. There are many elements in it, but they are divided into categories and we can understand these categories. ”

The classification of the manifest particle behavior may not seem so fundamental, but some experts, such as Xi-Gang Ven[Xiao-Gang Wen] from the Massachusetts Institute of Technology, says that the new rules of the emerging phases show how the elementary particles themselves can arise against the underlying network of entangled quantum information bits, which Ven calls "the ocean of qubits." For example, the “ string-network fluid ” phase , which is able to manifest itself in a three-dimensional qubit system, has disturbances that look exactly like the known elementary particles. “The real electron and the real proton can only be fluctuations of the string network,” says Ven.

New topological order

Before these phases suddenly appeared at zero temperature, physicists believed that they knew all the phases. By the 1950s, they could already explain what happens, for example, when water turns into ice, describing it as a violation of symmetry: if liquid water has rotation symmetry at the atomic level (it is the same in all directions), then in ice H ₂ O enclosed in columns and lines.

Everything changed in 1982 after the discovery of the fractional quantum Hall effect.manifested in a two-dimensional ultracold gas from electrons. The substance in such a state had manifested particles with charges in the fraction of electron charges that made fractions of steps in a one-sided walk around the perimeter of the system. “With the help of symmetry it was already impossible to distinguish such phases,” said Ven.

A new paradigm was required. In 1989, Wen introduced that such phases as the state of the fractional quantum Hall effect manifest themselves not on a plane, but on other topological sets — related surfaces like the surface of a sphere or a torus. Topology refers to the global, immutable properties of such spaces that cannot be changed by local deformation. As it is known, at least to topologists, you can turn a donut into a cup, deforming its surface, since both figures have one hole, and, therefore, they are topologically equivalent. But stretch and squeeze as much as you like, and even the most flexible donut cannot be turned into a pretzel.

Wen found that new properties appear in the phases of zero temperature in new topological conditions, and coined the term "topological order "describing the essence of these phases. Other theorists also discovered the connection of phases and topology. With the discovery of many different exotic phases - there are already so many that, as the researchers say, they barely have time to describe them - it became clear that topology and symmetry They offer a good system for their organization.

Topological phases manifest themselves only in the region of absolute zero, since only at such low temperatures can particle systems come to the ground quantum statewith the least energy. In the ground state, delicate interactions that establish the identity of the particles — disappearing at high temperatures — bind the particles into global systems using quantum entanglement. Instead of describing particles individually, mathematically they become components of a more complex function that describes them all at once, often with the emergence of new particles in the form of excitations of the global phase. The emerging schemes of long-range entanglement turn out to be topological, that is, insensitive to local perturbations — like the number of holes in the set.


Above: liquid phase of quantum spins. In this phase, a two-dimensional lattice of rotating particles leads to the appearance of loops of particles rotating in the same way. The number and location of the loops change all the time, and it all looks likelava lamp .

If this system is screwed onto a torus, it turns out that it can occupy four different, topologically invariant states:
A) Around the hole: an even number of loops / Through the hole: an even number of loops.
B) Even / odd.
C) Odd / odd.
D) Odd / even.

Despite the fact that the loops constantly experience quantum mechanical fluctuations, the topological order is always preserved (2 loops can go into 0 loops, which is also an even number).

Below: string-network fluid. If we wrap a system of changing and branching strings, then we also get various topologically invariant states.

Let us consider the simplest topological phase of the system called “liquid quantum spins”, consisting of a two-dimensional lattice of spins, or particles pointing up, down, or, with some probability, simultaneously in both directions. At zero temperature, the spin-liquid generates strings of spins pointing in one direction, down, and these strings form closed loops. The direction of the spins is subject to quantum-mechanical fluctuations, and the pattern of loops on the material also changes: the loops of the lower spins are combined into larger loops or split into smaller ones. In such a phase of liquid quantum spins, the ground state of the system is the quantum superposition of all possible loop patterns.

To understand why this entanglement scheme is a topological order, imagine, as Ven did, that the quantum-spin liquid spills on the surface of a torus, and some of the loops twist around its opening. Because of this, instead of getting one ground state associated with the superposition of all the loop patterns, the spin-liquid will exist in one of four different ground states associated with the four superpositions of the loop patterns. One state consists of all possible patterns of loops with an even number of loops surrounding the opening of the torus, and with an even number of loops passing through it. The other has the first number even and the second number is odd; for the third and fourth, these numbers, respectively, are odd / even and odd / odd.

And once in one of these states, the system remains in it, despite the fact that the loop pattern changes locally all the time. If, for example, the spin-fluid has an even number of loops surrounding the hole of the torus, then these two loops may touch and unite, and suddenly turn into a loop that does not surround the hole at all. The number of loops is reduced by two, but still remains even. The ground state of the system is a topologically invariant property that is resistant to local changes.

Quantum computers of the future can take advantage of this invariance. If you have four topological ground states that are independent of local disturbances or errors, “you will have a way to store quantum information, because your bit may indicate what state you are in,” explains Zalelet, who studied the topological properties of spin fluids and other quantum phases. Such systems as spin-liquid do not need to turn around the torus to have topologically protected basic states. Favorite sandbox researchers serves " toroidal code", a phase theoretically built by the FKS theorist Alexei Kitaev from the California Institute of Technology in 1997, and demonstrated in experiments over the past ten years. A toroidal code can exist on a plane and still maintain several basic states inherent in the torus surface. In essence, spin loops able to move from one edge of the system and appear on the other edge, and the loops twisted around the system are equivalent to loops around the opening of the torus. "We know how to build connections between our own properties of the fundamental states of the system on the torus and the corresponding behavior of the particles, "said Zalelet.

Spin-liquids may also exist in other phases in which the spins do not form closed loops, but branch out and form networks of strings. This is a string-network liquid phasewhich, according to Vienna, “can produce the entire Standard Model” of particle physics, starting from the three-dimensional ocean of qubits.

Phase Universe

Studies conducted by several groups in 2009 and 2010, completed the classification of “isolated” phases of matter that form in one dimension - chains of particles. The isolated phase is in the ground state: this low energy state is far enough away from the high energy states so that the system stably calms down in that state. Only isolated quantum phases produce well-defined particle excitations. The undivided phases are bubbling quantum soups, their properties for the most part remain unexplored.

For a one-dimensional chain of bosons - particles like photons, with a whole quantum spin (which means that they return to their original state after being swapped), there is only one isolated topological phase. In this phase, first studied by a theorist from Princeton Duncan Haldane , who won the 2016 Nobel Prize with David Tauless and John Michael KosterlitzFor decades of work on topological phases, the spin chain generates particles with a half-integer spin at both ends. A chain of fermions has two distinct topological phases (these are particles like electrons and quarks, with half-integer spins - which means that with a change of position, their state becomes negative). The topological order in these one-dimensional chains grows not from the long-range entanglement, but from the local symmetry connecting the neighboring particles. These phases are called “symmetrically protected topological phases” and correspond to “cocycles of cohomological groups ”, mathematical objects associated with such invariants as the number of holes in the set.


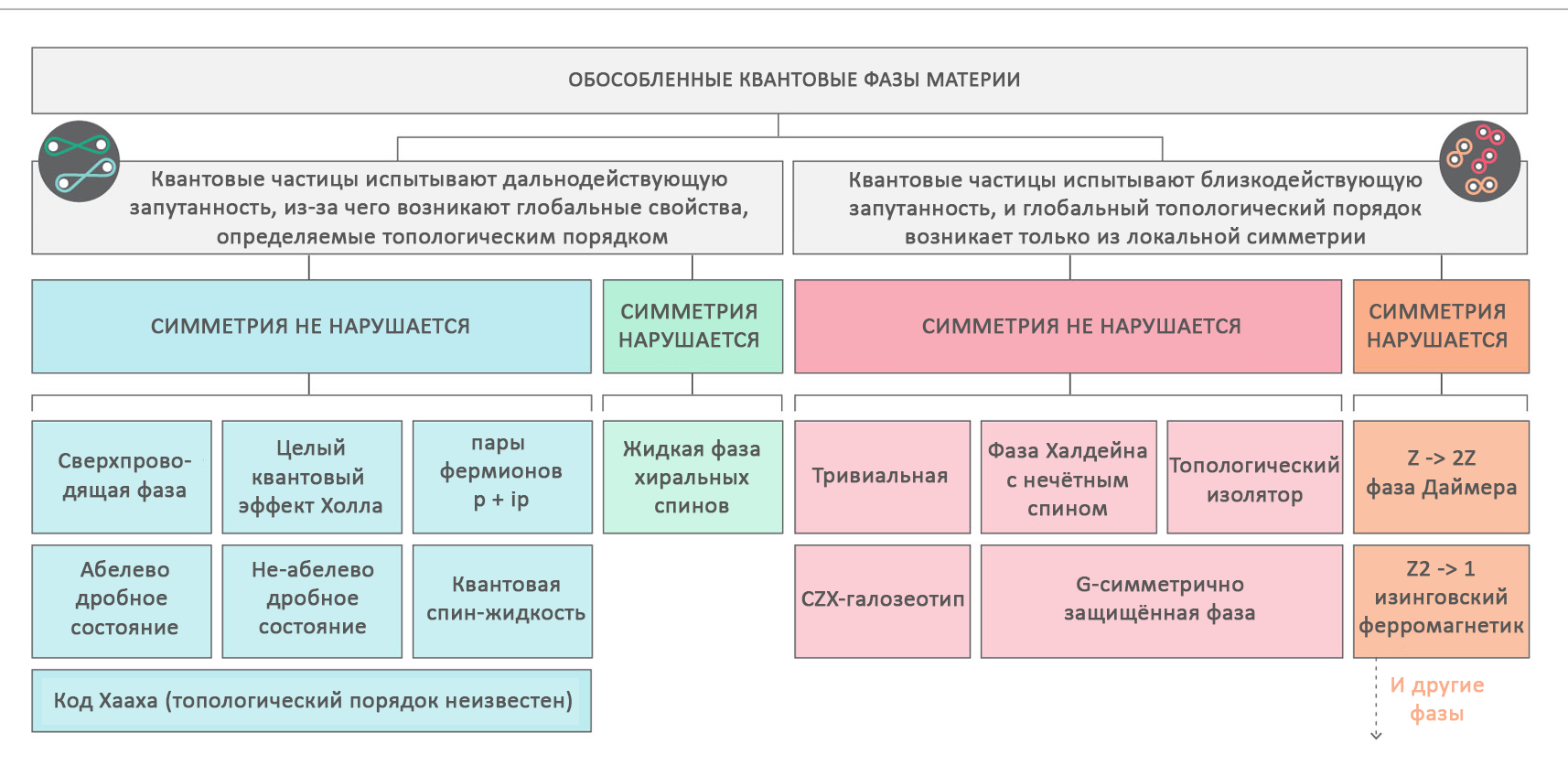
Periodic table of phases: the table presents typical examples of isolated phases, with a stable ground state. The classification is considered complete for one-dimensional and two-dimensional spaces. For three-dimensional spaces, so far little is known.

Two-dimensional phases are much more and they are much more interesting. They may manifest what some experts consider a “true” topological order: an order associated with long-range quantum entanglement, such as loop fluctuations in a spin-liquid. Over the past few years, researchers have shown that these entanglement schemes correspond to topological structures called tensor categoriesBy enumerating the different ways in which objects can merge and twist around each other. “Tensor categories provide a way to describe particles that consistently merge and are woven into braids,” said David Perez-García of the Complutense University of Madrid.

Researchers, such as Perez-García, are working on the mathematical proof that the well-known classes of two-dimensional isolated topological phases are complete. He helped graduate with one-dimensional classes in 2010using the conventional wisdom that these phases are always well approximated by quantum field theories — such mathematical descriptions in which the environment where quantum particles exist is considered smooth. “These tensor categories hypothetically cover all the two-dimensional phases, but so far there is no exact mathematical proof,” Perez-Garcia said. - Of course, it would be much more interesting if it were possible to prove that these are not all phases. Exotic things are always more interesting, because they have new physics, and they can be useful. ”

The nonsingular quantum phases represent another area of ​​opportunity for study, but are shrouded in mist impenetrable for most theoretical methods. “It’s impossible to speak the language of particles, and we start to face very serious difficulties,” says Sentil Todadri.[Senthil Todadri], a COP theorist from MIT. Non-isolated phases, for example, are the main obstacle to understanding high-temperature superconductivity. They make life difficult for researchers of quantum gravity, who joined the “all of the qubits” movement, believing that not only elementary particles, but also space-time and gravity appear due to entanglement schemes that exist in the underlying ocean of qubits. “We in“ all of the qubits ”spend a lot of time in working with non-isolated states, because it is from there that gravity appears - at least that’s what we think at the moment,” said Brian Swing , a theoretical physicist at the University of Maryland. Some researchers are trying to use the mathematical principle of duality.to turn a picture of a quantum soup into an equivalent particle description made in a higher dimension. “This should be regarded as a study of new territories,” Todadri says.

An even greater enthusiasm for researchers is visible in three-dimensional space. So far, it is clear that when the spins and particles are freed from the shackles of two-dimensionality and fill the three-dimensional space of reality, unimaginably strange systems of quantum entanglement begin to appear. “In three dimensions, there are still things that elude tensor categories,” says Perez-Garcia. “The excitement [of the fields] is completely wild.”

Haha code

And the wildest of the three-dimensional phases appeared seven years ago. A talented graduate of Calteh, Jongwan Haah [Jeongwan Haah] opened it with a computer simulation when he looked for the “dream code”: a basic quantum state that is reliable enough to safely store quantum memory even at room temperature.

To do this, Haah had to turn to three dimensions. In two-dimensional topological phases, such as a toroidal code, "string-like operators" introduce a significant proportion of errors: disturbances in the system, leading to the random formation of spin strings. These strings can sometimes wind new loops around the hole of the torus, changing the number of loops from even to odd and vice versa, transforming a toroidal code into one of the three other quantum states. Since the strings grow uncontrollably and turn around the rest, experts say that it is impossible to build a good quantum memory in the two-dimensional world.


Jionwan Haah

Haah wrote an algorithm for searching for three-dimensional phases, avoiding string operators. The computer issued 17 exact decisions which it then checked manually. It was confirmed that the four phases are free of stringed operators; one of the phases with the highest symmetry became known as the haha ​​code.

The Haha code is potentially useful for storing quantum memory, but at the same time, terribly strange. Xiao Chen, a FKS theorist from Caltech, recalls how she heard news of this, being a graduate student in 2011, a month or two after confusing Haach's discovery. “Everyone was shocked,” she says. “We didn’t know if we could do anything about it at all.” And today this situation persists for many years. ”

The Haha code on paper is quite simple: it is a two-member solution to an energy equation that describes spins interacting with its eight nearest neighbors in a cubic lattice. But the resulting phase "strains our imagination," Todadri said.

The peculiarity of the code are particle-like entities, fractons, which, unlike loop designs in quantum spin-liquid, are not liquid, and rest in place; fractons can only jump between their positions in the grid, if these positions are treated as a fractal pattern. That is, for example, in order to force the fractons standing at the vertices of the tetrahedron to swap places, it is necessary to infuse energy into each vertex of the system; but if we increase the scale, it turns out that what we considered to be apex actually turns out to be four vertices of a smaller, smaller tetrahedron, and we have to inject energy into all these vertices too. Increasing the scale, we again find an even smaller tetrahedron, and so on. This fractal behavior means that the Haha code never forgets the grid that is based on it, and it cannot be approximated by a smoothed description of the lattice, as is done in quantum field theory. Moreover, the number of basic states of the Haha code grows with the size of the underlying grid - and this property is definitely not topological (if you stretch a torus, it will still remain a torus).

The quantum state of the Haha code is extremely stable, since the fractal operator, ideally suited for it, is unlikely to appear randomly. Experts say that the implemented version of this code can be of great interest in terms of technology.

Phase Haha spawned a surge of theoretical reasoning. Haah helped with this when, in 2015, with two colleagues from MIT, he discovered many examples in the class of phases, now known as “fracton models,” simplified relatives of the Haaha code. The first model of this family was presented by Claudio Chamon from Boston University in 2005. Chen and other scientists studied the topology of fracton systems, some of which allow particles to move along lines or planes in three-dimensional space, as a result of which they can help with a conceptual understanding of what is happening or may be more suitable for experimental implementation. “This opens the way for many more exotic things,” says Chen about the Haaha code. - This is a demonstration of how little we know about the three-dimensional world and higher dimensions.

So far no one knows to which part of the landscape of possible phases the Haha code and its relatives belong, or how large the space of possibilities may be. According to Todadri, the community has made progress in the classification of the simplest isolated three-dimensional phases, but before the start of the full classification program, more research is needed. According to him, it is clear that "when we carry out the classification of isolated phases of matter in three-dimensional space, we will have to face such strange possibilities, one of which was first discovered by Haah."

Many researchers believe that to describe the fractal nature of the Haha code and to discover the full range of possibilities of three-dimensional quantum matter, new classification concepts may be needed. Ven said: “We need a new type of theory, a new thinking.” Perhaps, he said, we need a new picture of non-liquid long-range entanglement schemes. “We have some general ideas, but there is no systematic mathematics for their implementation,” he said. - We have a certain feeling of how it looks. A detailed systematization is not enough. But it is exciting. ”