Quantum-resistant blockchain
In this article I will talk about the security problem in the blockchain technology in the light of the growth performance of quantum computers, analyze some methods of protection against attacks using a quantum computer and the recently appeared project: Quantum-Resistant Ledger. According to the developers, this will be the first platform in the world, built on the principles of post-quantum encryption and designed to provide protection from the "quantum blow" in the event of the rapid development of these technologies. Platforms built using classical encryption principles can be subjected to such a blow. Without fundamental changes, Bitcoin, Ethereum, Ardor and most similar platforms may be in the near future.
Part 1. Security issue
Vulnerability
The algorithm for protecting Bitcoin and similar systems is based on the principle of asymmetric encryption with public and private keys. The transaction is signed by the private key, and its truth is verified using the public key.
Using classic attack algorithms, it is almost impossible to find the private key, knowing the public key. Asymmetric encryption systems such as RSA and the like (DSA, DH, etc.) are built on the premise that the complexity of decomposing a number into prime factors grows exponentially with the size of the key. However, using the Shor algorithm on a quantum computer, it becomes possible to decompose a number into prime factors in polynomial time and, thus, find the private key, knowing the public key.
In 2001, IBM demonstratedthis possibility, decomposing the number 15 into two simple factors 3 and 5. For these purposes, a quantum computer consisting of 7 qubits was used. Since then, the development of quantum computing technology is happening faster.
In 2016, a group of researchers from the Massachusetts Institute of Technology, together with the Innsbruck Institute, performs the same task of decomposing the number 15, using only 5 qubits .
In July 2017, a programmable 51 qubit computer was created by Russian-American physicists .
At the end of October 2017, an international research team from Singapore and Australian universities concluded that most cryptographic protocols used in the blockchain are vulnerable to attacks from a powerful quantum computer. ATThe group's report contains 2 predictions for the growth of the power of a quantum computer: optimistic and less optimistic. According to the first, the number of qubits of a quantum computer will double every 10 months. A less optimistic forecast suggests doubling the number of quits every 20 months. The figure below shows the graphs of both forecasts.
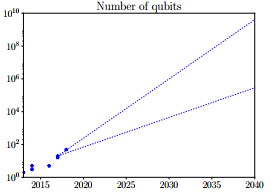
The algorithm for creating a digital signature based on elliptic curves ( ECDSA ) has been recognized as the most vulnerable to attacks by a quantum computer . Thus, according to the report of the group , Bitcoin in its classic form can be cracked by 2027.
Maybe not so bad? Public key is not stored in clear view
At the end of April 2017, an article is published on bitcoin.com to answer the question of whether Bitcoin holders should be wary of its hacking using a quantum computer. It says that in spite of the fact that asymmetric encryption is used in the Bitcoin blockchain, users do not have to fear for the safety of their coins. The public key is not stored in clear text. So, addresses for transferring coins are not public keys, but only the result of using the SHA-256 hash function. The hash function performs one-way conversion and is therefore resistant to attacks from a quantum computer.
The public key becomes known during the transaction.
The statement that the public key is not available in the clear, is not quite true. Without going into small details, let us look at Bitcoin (BTC) as an example of how cryptocurrency is transferred from one person to another.
Let Alice in her wallet on one of the Bitcoin addresses has 100 mBTC (1000 mBTC = 1 BTC). She wants to translate 1 mBTC to Bob. To do this, she indicates Bob’s Bitcoin address, transfer commission and Bitcoin address in her wallet to receive the change. Let Alice specify 1 mBTC as a commission. Thus, out of 100 mBTC Alice has, 1 mBTC is sent to Bob, 1 mBTC goes as a Bitcoin network commission and 98 mBTC is returned to Alice’s wallet.
Now let's look at what happens at the level of the Bitcoin network. Alice and Bob have purses containing addresses for storing coins. One wallet may contain several Bitcoin addresses. Addresses are generated when creating wallets. Each address corresponds to a pair of keys created by the ECDSA algorithm: public and private. During the transfer of coins, a transaction is created in which information about the number of coins transferred by Alice, Bob’s Bitcoin address, a signature made with Alice’s private key, Alice’s public key and some other data is transmitted . Further, the transaction in an open (unencrypted) form is sent to the network.. Network nodes, before accepting a transaction for processing, verify its signature using the public key. If the signature is valid, they add the transaction information to the block. Such an operation of inclusion is called confirmation.
The average block generation time in the Bitcoin network is 10 minutes. The network aims to keep this time constant. Before using the funds received, it is recommended to wait for 6 confirmations. Thus, Bob, while observing the safety rules, will be able to use the funds received about an hour after their transfer.
One of the features of the transfer of coins in the Bitcoin network is that it is not possible to transfer only part of the coins from one address. Coins are always transferred to the entire volume located on the Bitcoin address of the wallet, while the sender returns the change. It can be received both on the address from which the coins were sent, and on any other. Therefore, Alice must provide an address for delivery. In a number of software operating the wallet, the delivery address is the shipping address.
Commission for a transaction, strictly speaking, is not mandatory, but its absence can permanently postpone the execution of the transaction. The converse is also true: you can speed up the transaction a little by increasing the amount of commission. At the time of this writing (January 2018), most software wallets offer to specify a commission of 1 mBTC. There are a number of resources, for example, this one , which make it possible to estimate the time a transaction is included in a block depending on the size of the commission.
Use public key 1 time
From a security point of view, it is best to receive a change to a new address, the public key of which will be unknown to the network. In this case, the key pair is used only once. However, according to statistics, as of December 2017, about 41.34% of addresses are reused.
10 minutes to attack
However, sooner or later you will need to use the tools on the new address. The public key is transmitted to the network in the clear. Until a confirmation is received, the funds are still at the sender. If an attacker obtains a public key during a transaction, he will have about 10 minutes to obtain the private key using a quantum computer and try to conduct his transaction from the same address, setting a higher commission.
Static addresses are more vulnerable
In systems such as Ethereum, NXT, Ardor, and others, the public key also becomes known after the first transaction. The situation is aggravated by the fact that tokens or smart contracts are tied to static addresses that can be attacked for a long time. If the attack is successful, then the attacker will be able to destroy the entire economic system based on these addresses.
Part 2. Ways to solve
How to ensure resistance to attacks of a quantum computer?
Currently, there are several basic methods that provide protection against attacks from a quantum computer:
- hash based cryptography;
- code-based cryptography;
- matrix based cryptography;
- cryptography based on multidimensional quadratic systems;
- cryptography based on the secret key.
If there are sufficiently long keys and security requirements are met, these protection methods are able to withstand both classical attacks and attacks using a quantum computer.
The most studied is the use of digital signatures based on hash functions.
As mentioned earlier, the hash function performs one-way message conversion. The message is converted to a fixed-length hash value. Using the hash function on the one hand should make it meaningless to search through messages to get a similar hash value. On the other hand, the algorithm must be resistant to collisions: when the same hash function corresponds to 2 different messages.
Grover's quantum algorithmcan be used to try to find a collision or perform a preliminary attack to find the original message. This will require
Signature Lamport
One of the uses of the hash function in a digital signature is the Lamport signature. It can be built on the basis of any one-way hash function. The crypto-stability of the algorithm is based on the crypto-stability of the hash functions used.
Signature scheme
For the message  long
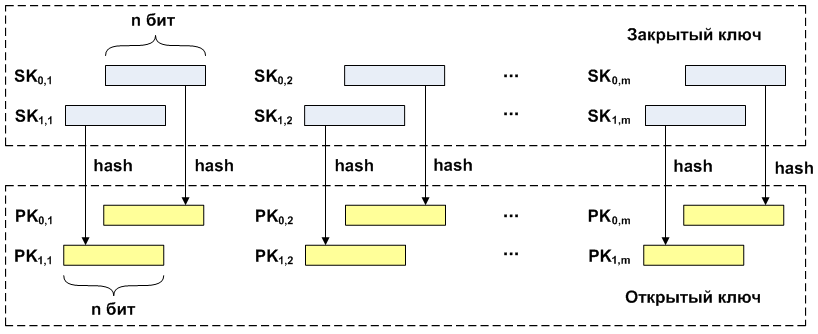
long  keys are generated. First, private keys are generated in pairs.
keys are generated. First, private keys are generated in pairs. long
long  then, using the hash function, public key pairs are formed from the private keys
then, using the hash function, public key pairs are formed from the private keys  . The number of pairs of private and public keys is equal to the number of bits in the original message.
. The number of pairs of private and public keys is equal to the number of bits in the original message.
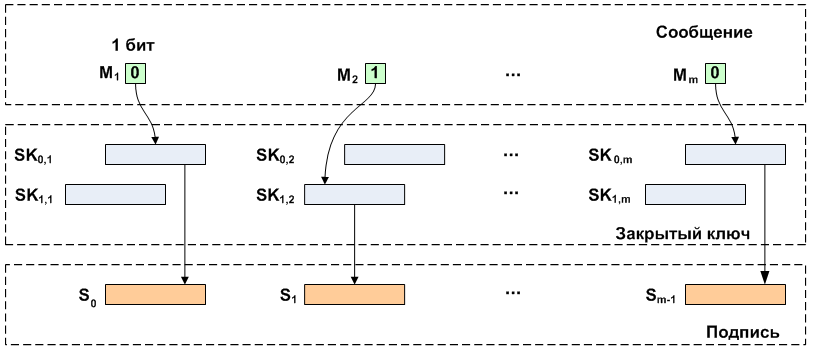
When executing a signature, the message is read bit by bit, and, depending on the value of the current bit, one of the private keys of the corresponding pair is selected. Selected private keys are combined into a signature. Next, the resulting signature and пар открытых ключей отправляются адресату.
пар открытых ключей отправляются адресату.
Проверка подписи похожа на процесс ее создания. Подпись разбивается на фрагменты длиной , которые затем преобразуются при помощи той же хеш-функции. Побитово читается сообщение и значением бита выбирается открытый ключ, который сравнивается с полученным значением хеша.
, которые затем преобразуются при помощи той же хеш-функции. Побитово читается сообщение и значением бита выбирается открытый ключ, который сравнивается с полученным значением хеша.
Как правило, перед применением подписи исходное сообщение хешируется для уменьшения его размера. Пусть в качестве хеш-функции выбрана SHA-256, тогда . При этом общая длина открытого (как и закрытого) ключа
. При этом общая длина открытого (как и закрытого) ключа  получается равной:
получается равной:
Длина подписи составляет:
составляет:

When executing a signature, the message is read bit by bit, and, depending on the value of the current bit, one of the private keys of the corresponding pair is selected. Selected private keys are combined into a signature. Next, the resulting signature and

Проверка подписи похожа на процесс ее создания. Подпись разбивается на фрагменты длиной
Как правило, перед применением подписи исходное сообщение хешируется для уменьшения его размера. Пусть в качестве хеш-функции выбрана SHA-256, тогда
Длина подписи
The signature of Lamport is a one-time (it remains safe only when it is used once), since during its execution and transfer, half of the private key becomes known. Let the message length be 256 bytes and the hash length be 256. Before Alice publishes the message signature, no one knows 2 * 256 random numbers in the secret key. Thus, no one can create the correct set of 256 numbers for the signature.
After Alice publishes the signature, no one will yet know the remaining 256 numbers, and thus cannot create a signature for messages that have a different hash.
The fact that Lamport's signature is one-time, in combination with an impressive total signature and public key (24 KB with a message length of 256 bytes and a hash length of 256 bytes), makes its use in a public transaction block impractical.
Signature Vinernytsia
There are other one-time digital signature algorithms. In the signature of the Winnernitz, in contrast to the signature of Lamport, the original message is signed not bit by bit, but by block. The one-time Winternitz signature, like Lamport, can be built on the basis of any strong cryptographic function.
Signature scheme
Сообщение  длиной
длиной  разбивается на фрагменты
разбивается на фрагменты  длиной
длиной  . Для каждого фрагмента генерируется закрытый ключ
. Для каждого фрагмента генерируется закрытый ключ  длины
длины  . К каждому закрытому ключу последовательно применяется операция хеширования
. К каждому закрытому ключу последовательно применяется операция хеширования  раз (раундов
раз (раундов  ). В результате проведенных операций получаются соответствующие им открытые ключи
). В результате проведенных операций получаются соответствующие им открытые ключи  той же длины
той же длины  .
.
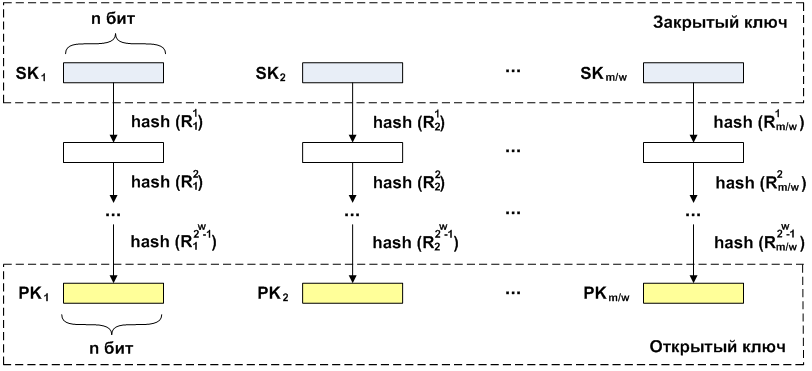
При подписи, как и при генерации публичных ключей, производится итеративное вычисление хеша над закрытыми ключами. Количество повторений в каждом случае зависит от подписываемого сообщения. Как уже говорилось ранее, сообщение разбито на блоки длины . Численное значение этого блока
. Численное значение этого блока  и является количеством итераций, которые необходимо выполнить над закрытыми ключами для получения подписи. Соединение полученных блоков и будет подписью данного сообщения.
и является количеством итераций, которые необходимо выполнить над закрытыми ключами для получения подписи. Соединение полученных блоков и будет подписью данного сообщения.
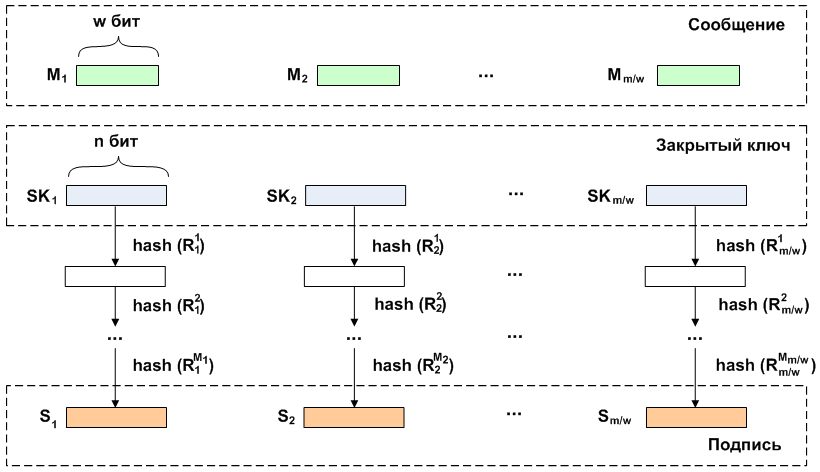
При проверке подписи над фрагментами ее длины производится итеративное вычисление хеша. Количество раундов
производится итеративное вычисление хеша. Количество раундов  применения хеш-функции определяется как разность между количеством итераций для получения открытого ключа и численного значения блока сообщения, т.е.
применения хеш-функции определяется как разность между количеством итераций для получения открытого ключа и численного значения блока сообщения, т.е.  раз. Затем полученные значения сравниваются с соответствующим публичным ключом.
раз. Затем полученные значения сравниваются с соответствующим публичным ключом.
При использовании SHA-256 в качестве хеш-функции для подписи Винтерница, .
.
Пусть бит. Тогда полный размер открытого ключа
бит. Тогда полный размер открытого ключа  и подписи
и подписи  равны:
равны:
Количество операций вычисления хеша в данном случае равно:
Для случая с , это значение возрастает до
, это значение возрастает до  .
.

При подписи, как и при генерации публичных ключей, производится итеративное вычисление хеша над закрытыми ключами. Количество повторений в каждом случае зависит от подписываемого сообщения. Как уже говорилось ранее, сообщение разбито на блоки длины

При проверке подписи над фрагментами ее длины
Пример
Проиллюстрирую вышесказанное небольшим примером. Пусть дано сообщение  (в битовом представлении) длины
(в битовом представлении) длины  , параметр Винтерница
, параметр Винтерница  и некоторая хеш-функция длины
и некоторая хеш-функция длины  :
:
Генерируем закрытых ключа на основе генератора псевдослучайных чисел. К каждому закрытому ключу применяем
закрытых ключа на основе генератора псевдослучайных чисел. К каждому закрытому ключу применяем  раз хеш-функцию, тем самым получая
раз хеш-функцию, тем самым получая  открытых ключа, которые объединяются в один общий ключ длины
открытых ключа, которые объединяются в один общий ключ длины  бит. Далее по каждому блоку сообщения
бит. Далее по каждому блоку сообщения  длины
длины  определяем количество применяемых к закрытому ключу операций хеширования
определяем количество применяемых к закрытому ключу операций хеширования  . В данном случае это будут значения
. В данном случае это будут значения  и
и  соответственно. Выполнив операцию хеширования на закрытых ключах получаем подпись длиной
соответственно. Выполнив операцию хеширования на закрытых ключах получаем подпись длиной  бит.
бит.
Для проверки подписи делим ее на части длиной . Над каждой частью производим
. Над каждой частью производим  операций хеширования. Т.е.
операций хеширования. Т.е.  и
и  раза соответственно. Если в результате проведенных операций получается значение совпадающее с открытым ключом, значит, сообщение достоверно.
раза соответственно. Если в результате проведенных операций получается значение совпадающее с открытым ключом, значит, сообщение достоверно.
Генерируем
Для проверки подписи делим ее на части длиной
При использовании SHA-256 в качестве хеш-функции для подписи Винтерница,
Пусть
Количество операций вычисления хеша в данном случае равно:
Для случая с
The sizes of the public key and the signature, with the same parameters as in the example for the signature of Lamport, are equal to 1 KB. In total, this is less than in the signature of Lamport (24 KB). However, the number of hash calculations is 8160. This is undoubtedly a lot. In addition, when verifying the signature, an average of half of this number of iterations is performed. This makes this signature option impractical for use in the blockchain.
There are several variants of the Winterternitz signature, including with the extension of the signature in order to increase reliability and reduce the number of applications of the hash function. Their description is beyond the scope of this article. Those who are interested can see more here . The use of the Winternitz signature on the basis of the national hash function GOST 34.11-12 can be viewedhere .
Merkle Tree (MSS)
One-time signatures can provide satisfactory cryptographic security; however, it is their disposability that can be a serious problem. Let it be necessary to transfer savings from one address to another. It turns out that when using one-time signatures, it will be necessary to transfer the entire amount of funds each time, and a new address will be required for each transaction. With each transaction you will need to publish a new public key. In addition, the preservation in the blockchain of new transactions will gradually require more time to search for them.
To solve the problem, the signature scheme is extended by holding several signatures based on several key pairs for each address. The use of several signatures is performed on the basis of a binary hash tree - the Merkle tree.
Read more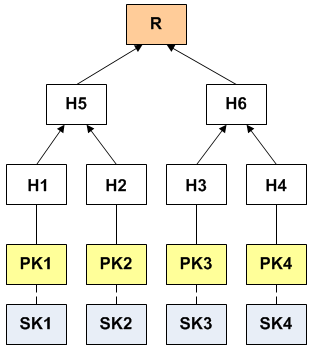
Вычисление дерева производится от листьев к корню. Каждый узловой лист дерева вычисляется как хеш от сгенерированного открытого ключа. Остальные узлы вычисляются путем получения хеша от конкатенации (склеивания) дочерних узлов. Таким образом рассчитывается все дерево до корня. Пусть есть 4 пары ключей, дерево Меркла рассчитывается вычислением 7-ми хешей (см. рисунок выше).
Особенностью дерева Меркла является то, что существование любого узла или листа может быть криптографически доказано путем вычисления корня.
Подпись сообщения создается при помощи закрытого ключа из выбранной пары ключей.
Проверка подписи подразумевает вычисление корня на основе переданных параметров и сравнение с ним как с многоразовым публичным ключом. Этими параметрами являются:
When using one-time Merkle or Winternitz signatures, there is no need to transfer a separately selected one-time public key, since it can be obtained from the message signature. It is enough to transfer its number reflecting its position in a tree. For example, in the figure above, the transmitted parameters will be: signature, root, sheet number - 0 (the sheet number with the key ) and hashes
) and hashes  and
and  . When performing a signature verification, the public key will be obtained from it.
. When performing a signature verification, the public key will be obtained from it. respectively hash
respectively hash  . Hashes
. Hashes and
and  will calculate
will calculate  . And hashes
. And hashes and
and  will calculate the root
will calculate the root  which can be compared with the value of the transferred root.
which can be compared with the value of the transferred root.

Вычисление дерева производится от листьев к корню. Каждый узловой лист дерева вычисляется как хеш от сгенерированного открытого ключа. Остальные узлы вычисляются путем получения хеша от конкатенации (склеивания) дочерних узлов. Таким образом рассчитывается все дерево до корня. Пусть есть 4 пары ключей, дерево Меркла рассчитывается вычислением 7-ми хешей (см. рисунок выше).
Особенностью дерева Меркла является то, что существование любого узла или листа может быть криптографически доказано путем вычисления корня.
Подпись сообщения создается при помощи закрытого ключа из выбранной пары ключей.
Проверка подписи подразумевает вычисление корня на основе переданных параметров и сравнение с ним как с многоразовым публичным ключом. Этими параметрами являются:
- подпись;
- корень;
- a one-time key, the closed part of which the message was signed;
- hashes from the tree, lying on the way from the selected sheet to the root.
When using one-time Merkle or Winternitz signatures, there is no need to transfer a separately selected one-time public key, since it can be obtained from the message signature. It is enough to transfer its number reflecting its position in a tree. For example, in the figure above, the transmitted parameters will be: signature, root, sheet number - 0 (the sheet number with the key
The Merkle tree, compiled and calculated from public keys, allows instead of publishing the entire set of them to publish only the root of the tree. This increases the size of the signature by including a part of the tree in the signature, but makes it possible using only 1 hash to verify many signatures. So, at the depth of the tree
The Merkle tree for keys based on an elliptic curve algorithm is used in Bitcoin and Ethereum, the latter with an excellent article on the Merckle tree .
Hypertree
The main disadvantage of the basic Merkle scheme is that the number of available signatures is limited, and all pairs of keys of one-time signatures must be generated before computing the Merkle tree. Key generation and signing time grow exponentially relative to the height of the tree. It is possible to delay the generation of new keys, as well as increase the number of available pairs using a hypertree.
Read more
Гипердерево представляет собой структуру, состоящую из деревьев Меркла. В этой структуре по назначению выделяются 2 типа деревьев: дерево сертификации и дерево подписи. Дереву подписи соответствуют ключи, используемые для подписывания сообщений. Дереву сертификации соответствуют ключи для подписывания корней деревьев подписи. Таким образом, деревья подписи являются дочерними к дереву сертификации (см. рисунок ниже).
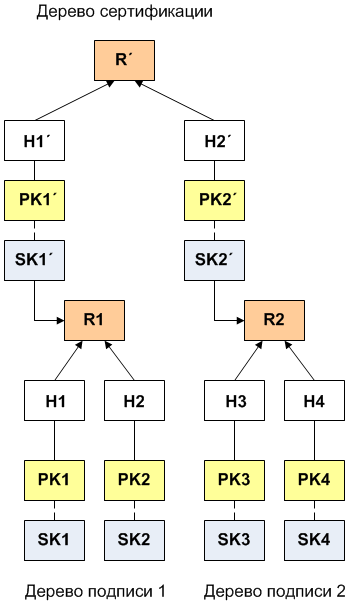
To verify the signature of the message in this case, the same parameters are transmitted as for a regular Merkle tree, but from both trees. Thus, the signature and its verification become somewhat more difficult, however, it becomes possible to flexibly expand the structure. While the size and number of signatures for each additional tree grows linearly, the total volume of signatures of the hypertree grows exponentially.
No need to build a hypertree symmetric. You can always add it with layers of new signature trees. Thus, the transaction block signatures will initially be small, which will increase as the depth of the hypertree increases.

To verify the signature of the message in this case, the same parameters are transmitted as for a regular Merkle tree, but from both trees. Thus, the signature and its verification become somewhat more difficult, however, it becomes possible to flexibly expand the structure. While the size and number of signatures for each additional tree grows linearly, the total volume of signatures of the hypertree grows exponentially.
No need to build a hypertree symmetric. You can always add it with layers of new signature trees. Thus, the transaction block signatures will initially be small, which will increase as the depth of the hypertree increases.
Expanded Merkle Tree Structure (XMSS)
A full description of the scheme goes far beyond the scope of this article; you can read more here . I will touch only the basic concepts and characteristics. The XMSS scheme, like the Merkle tree, allows you to extend one-time signatures. The use of a bit mask with the use of exclusive OR (XOR) of child nodes before the hashes are concatenated into the parent node allows increasing the resistance to collisions of the hash functions used. So, when using SHA-256 as a hash function in combination with the extended Winternitz scheme with a security parameter (W-OTS +), it allows to increase security from 128 to 196 bits. According to lenstraThe 196-bit protection is enough to consider it safe against an attack by simply iterating until 2169. With all the advantages of the XMSS scheme, its main drawback is the long key generation time.
Currently, there are other schemes for expanding the Merkle tree ( GMSS , CMSS ), which, in combination with one-time signature algorithms, can also be used in a blockchain that is resistant to attacks using a quantum computer.
Part 3. Implementation of ideas
Quantum-Sustainable Blockchain Project - QRL

In the second half of 2016, a group to develop a blockchain resistant to both classic attacks and attacks using a quantum computer is created by Doctor of Sciences P. Waterland. According to the results of the development of the theoretical part at the end of the same year, the main document of the blockchain being developed - the “white book” (white paper) was laid out in open access. Currently, the document is available in several languages, including Russian.
QRL Key Features
1. Signature scheme and security
The signature scheme is based on the Winternitz extended signature algorithm (W-OTS +, w = 16, SHA-256) based on XMSS communication structures. This approach allows you to generate addresses with the possibility of signing, avoiding the long computational delay observed when creating giant XMSS structures. Provides 196-bit protection with predictable security against an attack by simply iterating up to 2169.
2. Algorithm of consensus - proof of work (proof-of-work)
In the first iteration of the core network, a proof-of-work consensus algorithm was announced.
3. Floating Commission
Larger transaction sizes compared to other blocks of the transaction chain require payment for each transaction. According to Waterland, markets with an artificial commission (for example, Bitcoin) are not needed and contradict the ideal of an open blockchain. Each transaction, if it is accompanied by a minimum payment, must be as valid as any other. The amount of the minimum payment acceptable to miners should be floating and set by the market. Those. nodes (miners) must competitively establish the lower limit of payment among themselves. The absolute minimum value will be respected at the protocol level. Thus, miners will order transactions from the memory for inclusion in the block at their discretion.
4. Dynamic block reward calculation
Each new block created will include the first coinbase transaction containing the mining address for which the reward will be defined as the amount of remuneration for the coin rate with the total amount of commissions for transactions within the block.
5. The time spent by the blocks is 1 minute. The
time between the blocks in the Bitcoin network is approximately 10 minutes. With the required 6 confirmations, this additionally increases the time to wait for the transaction to complete. Newer transaction chain block schemes, such as Ethereum, are improved in this aspect and benefit from a shorter block time without losing security or centralizing miners due to the high rate of orphaned / obsolete blocks.
For a QRL, this time finding a block is 1 minute.
6. Adaptive block size
To avoid possible disputes, a ready-made adaptive solution based on the Bitpay proposal was used, which uses a multiplier to increase the block size.
7. Monetary unit - quantum
The base unit of currency is a quantum. Each quantum is divided into the smallest elements. Below are the names of all elements in ascending order:
| Element | Value |
|---|---|
| Shor | |
| Nakamoto | |
| Buterin | |
| Merkle | |
| Lamport | |
| Quantum |
Thus, each transaction involving part of a quantum is actually a very large number of Shore units. Transaction fees are calculated and posted in Shore units.
8. Accounts and addresses
User balances are stored on accounts. Each account is a unique, reusable address of a transaction chain block, indicated by a string starting with a “Q”.
The address is created by running SHA-256 on the Merkle root of the highest XMSS certification tree. To this is added a four-byte checksum, formed from the first four bytes of the double SHA-256 hash of the Merkle root, and the letter “Q”.
For example, in Python pseudocode, this will be described as follows:
Q + sha256(merkle root) + sha256(sha256(merkle root))[: 4]A typical account address is:
Qcea29b1402248d53469e352de662923986f3a94cf0f51522bedd08fb5e64948af479
Each account has a balance, denominated in quanta, divisible down to a single Shore unit. Addresses with each transaction use a new one-time signature key pair. The transaction count, called nonce, will increase with each transaction sent from the account. This allows wallets that do not store the entire chain of blocks to track their location in the hypertree's signature scheme while maintaining state.
The current state of the project and future plans
After the release of the white paper, the group was replenished with several new developers and work began on translating what was planned. On the project site there are regular reports on the work done. And by April 2017, the QRL blockchain test network has already been launched. The source code of the project is laid out on Github. The project is actively discussed on Bitcointalk and Reddit.
In May 2017, an ICO was held in the Ethereum ecosystem. Released QRL token standard ERC20. A total of 65 million tokens were released. Of these, 52 million tokens are in circulation. Over the next 200 years, another 40 million coins will be issued. Thus, the total volume of the issue will be 105 million coins. When you run the main network, these tokens can be exchanged for QRL coins in a 1: 1 ratio. Currently, tokens are available for purchase on such exchanges as Bittrex, Upbit and Liqui. QRL quotes, according to coinmarketcap.com , are presented in the figures below.
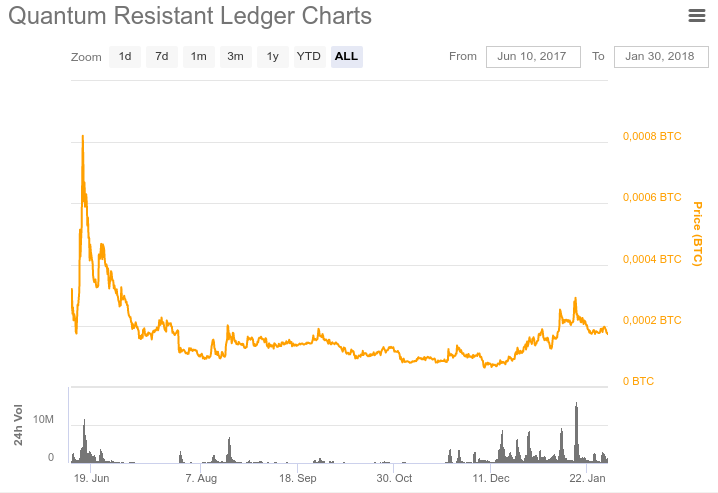
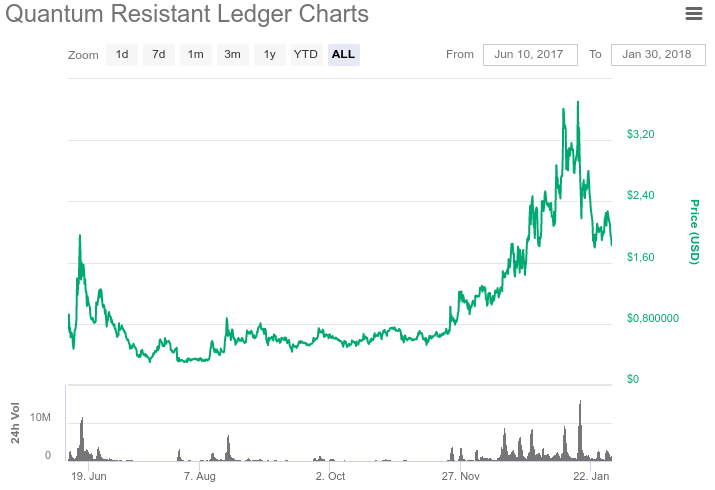
The launch of the main network is scheduled for February-March 2018.
In the future, it is planned to change the algorithm of consensus from the confirmation of the work to the confirmation of the stake (proof-of-stake). The expected safe time of the blocks will be 15-30 seconds.
Conclusion
The progress of quantum technologies has been launched and cannot be stopped. As more and more productive quantum machines appear, the spectrum of the problems they solve will continuously grow. Hacking existing cryptographic protection unsuitable for attacks from a quantum computer has long been one of the central themes of many security forums .
QRL is the first blockchain technology designed to solve this problem. In the future, of course, there will be others. Which of them will be the most successful - time will tell.
Acknowledgments
The author is grateful to Kamnik for the preparation of a significant part of the material and, especially, for the technical part, as well as SannX for constructive criticism and editing.
Links
- Shor algorithm .
- Decomposition of the number 15 into prime factors on a quantum computer (IBM) .
- Decomposition of the number 15 into prime factors on a quantum computer (MIT) .
- A report on experiments on 51 qubit computers .
- The report of the International Study Group on the stability of Bitcoin in front of a quantum computer .
- Using the ECDSA key generation algorithm in the Bitcoin blockchain .
- On the resistance of Bitcoin to attacks of a quantum computer .
- Confirmation of transactions in the Bitcoin network .
- Information about commissions in the Bitcoin network .
- Bitcoin address reuse statistics .
- Grover's quantum algorithm .
- Extended signature Vinternitsa .
- The use of one-time signature Winterternica based on the hash function GOST 34.11-12 .
- Geektimes about Ethereum .
- XMSS scheme .
- Lenstra. Choosing the size of cryptographic keys .
- GMSS .
- CMSS .
- Rates of cryptocurrency systems .
- Annual Post-Quantum Security Forum .
