Cartesian tree: Part 3. Cartesian tree by implicit key

Table of contents (currently)

Part 1. Description, operations, applications.
Part 2. Valuable information in the tree and multiple operations with it.
Part 3. Cartesian tree by implicit key.
To be continued ...

Very strong witchcraft

After all the heaps of opportunities that the Cartesian tree gave us in the previous two parts, today I will do something strange and sacrilegious with him. Nevertheless, this action will allow us to consider the tree in a completely new hypostasis - as a kind of advanced and powerful array with additional features. I will show how to work with it, I will show that all operations with data from the second part are saved for the modified tree, and then I will give some new and useful ones.

Recall once again the structure of deramide. It contains the key x , by which the deramide is a search tree, the random key y , by which the deramide is a bunch, and also, possibly, some user information with(cost). Let's do the impossible and consider the deramide ... without the keys x. That is, we will have a tree in which the key x is not at all, and the keys y are random. Accordingly, why it is needed is generally incomprehensible :)

In fact, to consider such a structure is like a Cartesian tree, in which the keys x are still somewhere, but they were not informed to us. However, they swear that for them, as expected, the condition of the binary search tree is fulfilled. Then we can imagine that these unknown X's are numbers from 0 to N-1 and implicitly arrange them according to the structure of the tree:

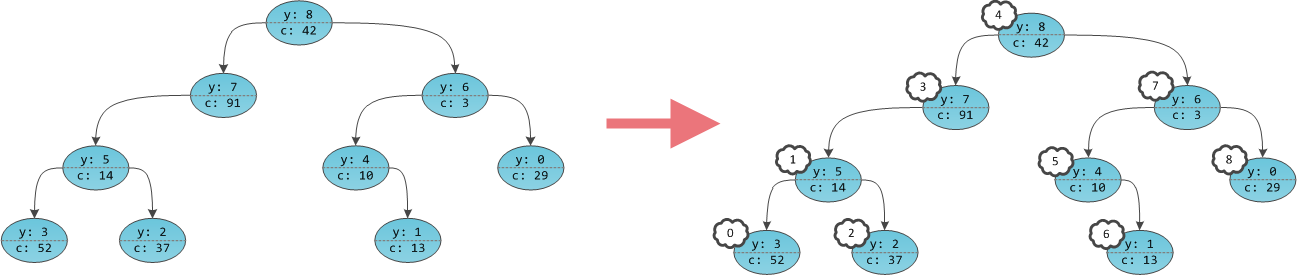
It turns out that in the tree it’s as if the keys at the vertices are not affixed, but the vertices themselves are numbered. Moreover, they are numbered in the in-order bypass order already familiar from the last part. A tree with clearly numbered vertices can be considered as an array in which the index is the same implicit key, and the content is user information c. Players are needed only for balancing; these are internal details of the data structure that are unnecessary for the user. X is actually not in principle, they do not need to be stored.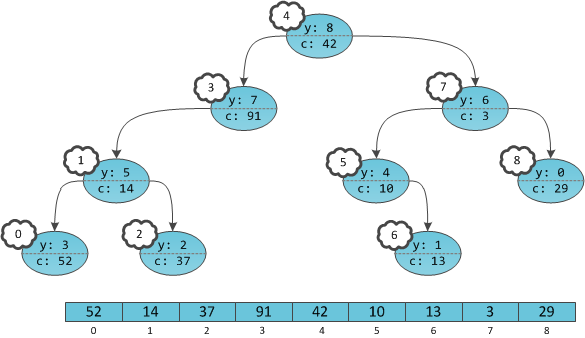

Unlike the previous part, this array does not automatically acquire any properties, such as sorting. After all, we do not have any structural restrictions on the information, and it can be stored at the tops anyhow.

Main applications

Now it’s worth talking about why such an interpretation is needed at all.
For example, have you ever wanted to merge two arrays? That is, simply ascribe one of them to the end of the other, without having to copy all the elements of the second one in O (N) in a loop. With the Cartesian tree by implicit key, you have such an opportunity: after all, no one took away the Merge operation from us.

Stop-stop-stop, but Merge was written for an explicit Cartesian tree. So her algorithm will have to be reworked here? Not really. Look again at her code.

public static Treap Merge(Treap L, Treap R)
{
    if (L == null) return R;
    if (R == null) return L;
    if (L.y > R.y)
    {
        var newR = Merge(L.Right, R);
        return new Treap(L.x, L.y, L.Left, newR);
    }
    else
    {
        var newL = Merge(L, R.Left);
        return new Treap(R.x, R.y, newL, R.Right);
    }
}

The Merge operation, you will remember, it is believed that all the keys of the left input of the tree L does not exceed the right of the input keys of the tree the R . Under the assumption that this condition is fulfilled, it merges without paying attention to the keys in principle: in the process of executing the algorithm, only priorities are compared.

It turns out that you and I are deceiving the Merge operation here in the most arrogant way: she expects that she will be given trees with ordered keys, and we palm off the trees without keys at all :) However, the assumption that there are explicit keys in the trees and they are ordered will force her merge the trees so that the keys L appear to be in the tree structure in some sense earlier than the keys R - because the condition of the search tree must be satisfied. That is: if in the tree L there were N elements, and in the tree R, respectively, M elements, then after the merge the elements of the tree R will automatically acquire implicit numbers from N to N + M-1. According to the tree structure, the Merge operation will automatically distribute them appropriately, and the priorities that it takes into account will perform “quasi-balancing”. Thus, we kind of attributed the “array" R to the "array" L on the right.

As for the sources, we only need to get a new data type ImplicitTreapwithout a key x, and for it the corresponding private constructor. All Merge code will remain the same. Of course, this is when you consider that here is the version without calculating multiple queries - the functions of "restoring justice" and "pushing promises", implemented in the second part, will also remain in Merge in their old places.

For clarity, I will take two random implicit Cartesian trees and give them in the figure along with the merge result. Priorities are chosen randomly, so the real structure of both trees and the result can be very different. But it doesn’t matter - the structure of the array, i.e. the order of the elements cis always preserved.
The orange arrow is the recursion path in Merge.


Now it's time to split. It’s not so easy to deceive her: the Split operation, on the contrary, is not interested in priorities, it only compares the keys. You’ll have to think about how she will compare the peaks in the implicit tree. Although the problem actually lies higher: what does the Split operation do in the new data structure? She used to cut a tree with a key, but here we don’t have keys for which we need to cut.

There are no keys, however there is their implicit representation - array indices. Thus, the essence of cutting has changed somewhat: we want to split the tree into two so that exactly x ₀ elements appear in the left , and all the others in the right. In the “massive” interpretation, this means separating from the array x ₀ elements from the beginning into a new array.

How to perform a new Split operation? It considers, as before, two cases, the root of T will result in the left L or right of the R . It will appear in the left if its index in the array is less than x ₀ , otherwise in the right. And what is the index of the top of the tree in the array? We already know how to work with him from the second part: it is enough to store the sizes of subtrees at the tops of the tree . Then the selection process is easily restored.

Let S _L be the size of the left subtree ( T.Left.Size).
If S _L +1 ≤ x ₀, then the root will be in the left result. So, you need to recursively cut the right subtree. But cut by another key, by x ₀ -S _L -1 , because S _L +1 the element already fell into the desired left result.
If S _L +1> x ₀ , then the root will be in the right result. Now you need to recursively cut the left subtree. This case is not quite symmetrical, as before: we cut the subtree all with the same key x ₀ , because at this step, the recursions split the elements into the right result, and not the left one.

The figure shows a Cartesian tree with affixed subtrees and split in x ₀= 6 .

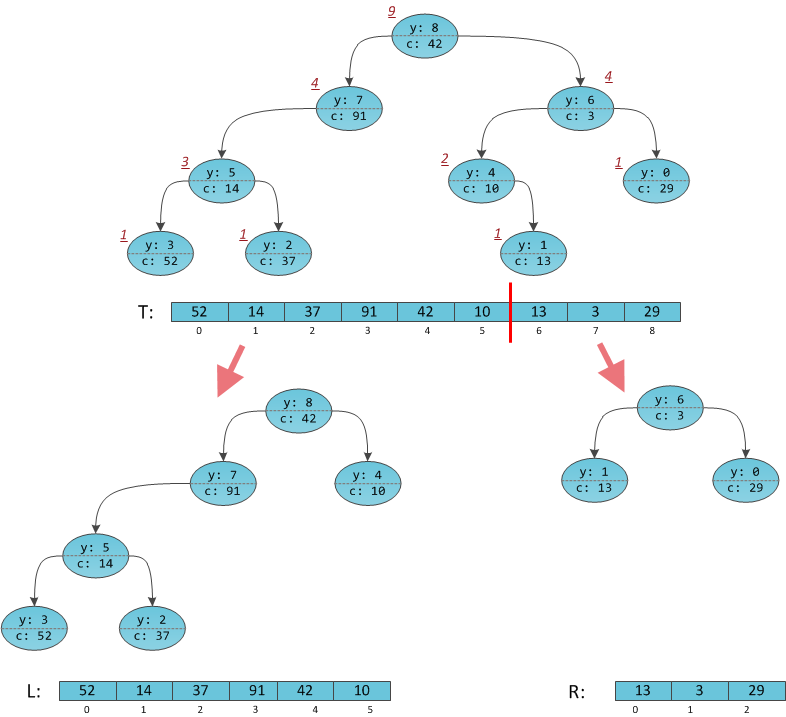
The source code for the new Split, along with a new class workpiece, is keyless and with another private constructor.
I give Split again so far without multiple operations - the reader can restore these lines independently, they have not disappeared from their old places. But we must not forget about recounting the size of subtrees.

private int y;
public double Cost;
public ImplicitTreap Left;
public ImplicitTreap Right;
public int Size = 1;    
private ImplicitTreap(int y, double cost, ImplicitTreap left = null, ImplicitTreap right = null)
{
    this.y = y;
    this.Cost = cost;
    this.Left = left;
    this.Right = right;
}
public static int SizeOf(ImplicitTreap treap)
{
    return treap == null ? 0 : treap.Size;
}
public void Recalc()
{
    Size = SizeOf(Left) + SizeOf(Right) + 1;
}
// теперь после заготовки - собственно Split
public void Split(int x, out ImplicitTreap L, out ImplicitTreap R)
{
    ImplicitTreap newTree = null;
    int curIndex = SizeOf(Left) + 1;
    if (curIndex <= x)
    {
        if (Right == null)
            R = null;
        else
            Right.Split(x - curIndex, out newTree, out R);
        L = new ImplicitTreap(y, Cost, Left, newTree);
        L.Recalc();
    }
    else
    {
        if (Left == null)
            L = null;
        else
            Left.Split(x, out L, out newTree);
        R = new ImplicitTreap(y, Cost, newTree, Right);
        R.Recalc();
    }
}

Now that we have written for the array Split and Merge, which work in logarithmic time, it is time to use them somewhere. Let's play around with the array.

Games with an array

Insert

Focus No. 1 - we will insert an element inside the array at the required position Pos for O (log ₂ N), and not for O (N), as usual.

In principle, we already know how to do this with ordinary Cartesian trees, only now the index has replaced the key. And the rest of the procedure has not changed.

• We cut the array T [0; N) by the index Pos on arrays L [0; Pos) and R [Pos; N) .
• We make an array-tree from one vertex from the inserted element.
• Assign the created array to the right to the left result L, and to both of them - the right result R.
• Received the array T '[0; N + 1) , in which the desired element is at the position Pos, and the rest of the right-hand side is shifted.

The source code of the insert has not changed completely.

public ImplicitTreap Add(int pos, double elemCost)
{
    ImplicitTreap l, r;
    Split(pos, out l, out r);
    ImplicitTreap m = new ImplicitTreap(rand.Next(), elemCost);
    return Merge(Merge(l, m), r);
}

Delete

Focus No. 2 - we cut out an element from the array that is at this position Pos .

Again, the procedure is the same as with ordinary Cartesian trees.

• We cut the array T [0; N) by the index Pos on arrays L [0; Pos) and R [Pos; N) .
• The right result R is cut by index 1 (unit!). We get the array M [Pos; Pos + 1) from one element (standing earlier at the Pos position), and the array R '[Pos + 1; N) .
• Merge the arrays L and R '.

Download Source Code:

public ImplicitTreap Remove(int pos)
{
    ImplicitTreap l, m, r;
    Split(pos, out l, out r);
    r.Split(1, out m, out r);
    return Merge(l, r);
}

Multiple requests per segment

Focus # 3: for O (log ₂ N), you can also perform all the same multiple queries on the array sub-segments (sum / maximum / minimum / presence or number of labels, etc.).

The tree structure does not change from the previous part: at the vertex we store the parameter corresponding to the desired value calculated for the entire subsegment. At the end of Merge and Split, the same call is inserted Recalc(), recalculating the value of the value at the vertex based on the calculated parameters in its descendants.

Request for the segment [A; B) uses the standard method: cut the desired segment from the array (not forgetting that after the first cut, the desired index in the right result has decreased!) And return the value of the parameter stored in its root.
Source code - as an example, for maximum.

public double MaxTreeCost;
public static double CostOf(ImplicitTreap treap)
{
    return treap == null ? double.NegativeInfinity : treap.MaxTreeCost;
}
public void Recalc()
{
    Size = SizeOf(Left) + SizeOf(Right) + 1;
    MaxTreeCost = Math.Max(Cost, Math.Max(CostOf(Left), CostOf(Right)));
}
public double MaxCostOn(int A, int B)
{
    ImplicitTreap l, m, r;
    this.Split(A, out l, out r);
    r.Split(B - A, out m, out r);
    return CostOf(m);
}

Multiple operations on a segment

Focus No. 4: now for O (log ₂ N) we will perform operations from the second part on the sub-segments of the array: adding a constant, painting, setting to a single value, etc.

With working Merge and Split, the implementation of deferred calculations in the Cartesian tree is completely unchanged. The basic principle of work is the same: before performing any operation, “push a promise” to descendants. If you also need to support multiple queries from the previous section, after the operation you need to "restore justice."

To perform an operation on a segment, you first need to cut this segment from the tree with two Split calls, and then paste it again with two Merge calls.
For the lazy, I bring the complete source code for adding, along with the new Merge / Split implementations (they differ by as much as 1-2 lines), as well as with the push function Push:

public double Add;
public static void Push(ImplicitTreap treap)
{
    if (treap == null) return;
    treap.Cost += treap.Add;
    if (treap.Left != null) treap.Left.Add += treap.Add;
    if (treap.Right != null) treap.Right.Add += treap.Add;
    treap.Add = 0;
}
public void Recalc()
{
    Size = SizeOf(Left) + SizeOf(Right) + 1;
}
public static ImplicitTreap Merge(ImplicitTreap L, ImplicitTreap R)
{
    // проталкивание!
    Push( L );
    Push( R );
    if (L == null) return R;
    if (R == null) return L;
    ImplicitTreap answer;
    if (L.y > R.y)
    {
        var newR = Merge(L.Right, R);
        answer = new ImplicitTreap(L.y, L.Cost, L.Left, newR);
    }
    else
    {
        var newL = Merge(L, R.Left);
        answer = new ImplicitTreap(R.y, R.Cost, newL, R.Right);
    }
    answer.Recalc();
    return answer;
}
public void Split(int x, out ImplicitTreap L, out ImplicitTreap R)
{
    Push(this); // проталкивание!
    ImplicitTreap newTree = null;
    int curIndex = SizeOf(Left) + 1;
    if (curIndex <= x)
    {
        if (Right == null)
            R = null;
        else
            Right.Split(x - curIndex, out newTree, out R);
        L = new ImplicitTreap(y, Cost, Left, newTree);
        L.Recalc();
    }
    else
    {
        if (Left == null)
            L = null;
        else
            Left.Split(x, out L, out newTree);
        R = new ImplicitTreap(y, Cost, newTree, Right);
        R.Recalc();
    }
}
public ImplicitTreap IncCostOn(int A, int B, double Delta)
{
    ImplicitTreap l, m, r;
    this.Split(A, out l, out r);
    r.Split(B - A, out m, out r);
    m.Add += Delta;
    return Merge(Merge(l, m), r);
}

A small digression about permitted operations:

In fact, the recursive tree structure and deferred calculations allow you to implement any monoid operation. A monoid is a set with the binary operation ◦ given on it, which has the following properties:
• Associativity - for any elements a, b, c we have (a ◦ b) ◦ c = a ◦ (b ◦ c) .
• The existence of a neutral element - in the set there is an element e such that for any element a, a ◦ e = e ◦ a = a .
Then, for such an operation, it is possible to implement a tree of segments , and for similar reasons, a Cartesian tree.

Flip array

Focus No. 5 is a subsegment flip, that is, a rearrangement of its elements in reverse order.

And at this point I will stop in more detail. Turning an array is not a monoidal operation — frankly, it is not a binary operation at all on any set — but nonetheless. The uniqueness of this task is that you can come up with a push function for it. And since there is an opportunity to push through the operation, it means that you can realize it as a pending one.

So, we will store a Boolean value at each vertex - the overturn bit. This will be a deferred promise "this segment of the array needs to be deployed in the future." Then, on the assumption that we can push this bit to the descendants with a peculiar version of the functionPush, the tree always remains up to date - before any operations of accessing the elements of the array (search), as well as at the beginning of Merge and Split, a push is performed. It remains to figure out how to produce this “fulfillment of a promise”.

Suppose that at some vertex T there is a promise to invert the subsegment. To actually begin to fulfill it, it is enough to do the following:
• Remove the promise at the current vertex:

  T.Reversed = false;

• Swap his left and right sons.

  temp = T.Left;
  T.Left = T.Right;
  T.Right = temp;

• Change the promise to posterity. Please note: do not set to true (we do not know whether this bit has been with the descendants so far!), But change it. The operation ^ is used for this.

  T.Left.Reversed ^ = true;
  T.Right.Reversed ^ = true;

Indeed, what is “actually flipping an array”? Take two pieces of this array (subtrees), swap them in reality, and promise to flip these two subarrays in the future. It is easy to see that when all the promises are fulfilled to the end, the elements of the original array will be inverted.

Note - with ordinary Cartesian trees such a fraud cannot be carried out, since we violate the property of the search tree - the keys in the right subtree are less than the keys in the left. But since there are no keys at all in the implicit Cartesian tree, and the property is always respected for indexes, nothing breaks in the tree.

The user-defined function of turning over a segment works on an invariable principle, like any other operation: cut the desired segment, set a promise in its root, and paste the segment back. Here is the source code for the push and flip functions:

public bool Reversed;
public static void Push(ImplicitTreap treap)
{
    if (treap == null) return;
    // не установленное обещание - не проталкивается
    if (!treap.Reversed) return;
    var temp = treap.Left;
    treap.Left = treap.Right;
    treap.Right = temp;
    treap.Reversed = false;
    if (treap.Left != null) treap.Left.Reversed ^= true;
    if (treap.Right != null) treap.Right.Reversed ^= true;
}
public ImplicitTreap Reverse(int A, int B)
{
    ImplicitTreap l, m, r;
    this.Split(A, out l, out r);
    r.Split(B - A, out m, out r);
    m.Reversed ^= true;
    return Merge(Merge(l, m), r);
}

Now you can solve the classic interview task in a completely new way :)

Loop Array

Focus # 6: cyclic shift. The essence of this operation, for those who do not know, is easier to explain in the figure.

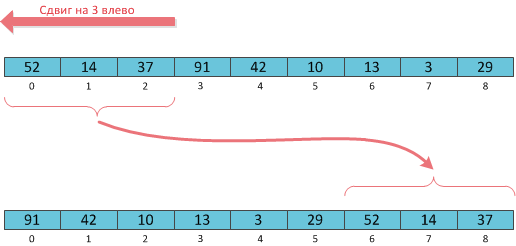
Of course, a cyclic shift can always be performed in O (N), but by implementing the array as an implicit Cartesian tree, you can shift it in O (log ₂ N). The procedure of shifting left by K is trite: we cut the tree at the index K, and glue it in the reverse order. The shift to the right is symmetrical, only you need to cut by the NK index .

public ImplicitTreap ShiftLeft(int K)
{
    ImplicitTreap l, r;
    this.Split(K, out l, out r);
    return Merge(r, l);
}

Again: the operation is unique to Cartesian trees by an implicit key, since gluing two Split results, whether they are ordinary Cartesian trees, is unacceptable: after all, Merge expects ordered trees from us, and we feed arguments to it in the wrong order.

Summary

A Cartesian tree by implicit key is a simple representation of an array in the form of a tree, which allows you to perform a bunch of operations with it and with its subarrays in logarithmic time. At the same time, O (N) is still wasting memory. Of course, using O-notation, I slightly crooked my heart, because in real life the actual memory occupied by the tree is important, and the Cartesian tree is famous for its overhead. Judge for yourself: N for information, N for priorities, 2N for links to descendants, N for the sizes of subtrees - this is a living wage, and if you add multiple requests, we get another N for each operation. You can improve your life a little by creating priorities from information.however, this is, firstly, a drop in the ocean (just minus N), and secondly, it is fraught with consequences from a security point of view: if someone finds out the function by which you create priorities, then he will be potentially able to give you new records to be created in a malicious manner to greatly unbalance the Cartesian tree. In the end, a situation is possible when all your data will noticeably slow down - although such cases, of course, are read and require remarkable work. You can get rid of the danger using different primes P for different vertices of the tree ... but this is a topic for a separate scientific study. For me personally, the capabilities of the Cartesian tree and the simplicity of its code are advantages that exceed the problem of high memory consumption. Although, of course, the program is different for the program.

From interesting facts: in Western literature, articles and the Internet, I could not find a single mention of the Cartesian tree by an implicit key. Of course, no one knows what it should be called in English terminology - however, questions on the forums and StackOverflow also led to nothing. In the Russian practice of sports programming ACM ICPC, this structure was used for the first time in 2000, invented by a member of the Kitten Computing team Nikolai Durov - a numerous winner of international competitions (however, Runet knows his brother Pavel more , as well as their joint creation ).

The obligatory program on the Cartesian tree I end with. Most likely, there will be at least one or two parts later - about alternative implementations of tree operations, and about its functional implementation - however, the three already written in principle make up enough ammunition for the full use of deramide in life. Thanks to everyone who honestly wrestled with me through the lines of this tutorial :) I hope you were interested.