An electronic digital signature for dummies: what it is with and how not to choke. Part 3
Part 1
Part 2
In this part, we will make a small digression from digital signatures towards that without which directly digital signatures, and information protection in the usual sense, would not be: encryption. After all, the first thing that comes to mind when it comes to protecting our data is not to give this data to a bad person to read. Therefore, before continuing to consider PGP and S / MIME standards, it’s worthwhile to fill out some of the blank spots in the knowledge and consider the encryption process in more detail.
Ciphers and codes exist, probably, from the moment humanity learned to record its impressions of the world around it on media. If you think about it a bit, even the ordinary alphabet is already a cipher. After all, when we read any text, in our head each drawn symbol is associated with a certain sound, a combination of sounds, or even a whole concept, and in the head of a neighbor who cannot read, this does not happen anymore.
Not knowing which symbol and what is compared, we can never understand what exactly the writer meant. For example, try to take and read something written in Hebrew, or in Chinese. The alphabets of these languages themselves will be an insurmountable obstacle for you, even if the concepts of your native language are written using these symbols.
But, nevertheless, just using someone else's alphabet is still not a sufficient measure to protect your data. Indeed, any alphabet, one way or another, was created for the convenience of using it and is inextricably linked with the language to which this alphabet is characteristic. So, having learned this language and a certain set of basic concepts in it (or simply using the services of a person who knows this language), a bad person can read your information.
So, you need to come up with an alphabet that only a limited circle of people know, and use it to write down information. Surely everyone read (or at least heard) a series of stories about Sherlock Holmes. An alphabet composed of dancing people appeared in this cycle (and many, I think, in childhood made up their own based on it). However, as this story shows, an observant person can figure out which symbol and what it refers to. So our information will fall into the wrong hands again.
What to do? Coming up more and more complex alphabets? But the more complex and cumbersome the alphabet, the more inconvenient to work with it, to keep it secret. In addition, there is a wonderful saying about secrecy: two people know - they know everything. After all, the weakest link in any cipher is a person who knows how to decrypt this cipher.
And why not make the encryption method immediately known to everyone, but it would be impossible to decrypt our data without some kind of key? After all, the key (unlike the entire alphabet) is small, it is quite easy to make a new one, if that (again, unlike the processing of the entire alphabet) is easy to hide. The most obvious advantages of key systems are shown in the following example: the recipient needs to read the message you sent. Plain, on paper. Let's say you use the secret alphabet. Then, in order to read the message, the recipient must know the alphabet, have a large dusty Talmud, which describes the decryption methods (because the alphabet must be complex in order to be reliable) and understand how to work with this Talmud. With the keys, everything is simpler: you put the message in the box with the lock, and the recipient just needs to insert the appropriate key, and know
So, well-known “alphabets” and keys are a mechanism that is much more convenient than just alphabets. But how is it possible to encrypt so that everything is decrypted with a simple key? And here, mathematics comes to our aid, and more specifically, mathematical functions that can be used to replace our original characters with new ones.
Recall what a function is. This is a certain ratio, according to which another can be obtained from one number. Knowing x and substituting it into the relation y = A * x known to us, we always get the value of y. But, as a rule, the opposite is also true: knowing y, we can get x.
As a rule, but not always. For many dependencies, getting y is easy, while x is already very difficult, and it takes a long time to get it. It is precisely on such dependencies that the encryption currently in use is based.
But back to the encryption itself. Encryption is divided into symmetric , asymmetric and combined . Consider the essence of each of them.
Symmetric EncryptionBy and large, it differs only slightly from the good old secret alphabet. As a matter of fact, it differs just in the presence of a key - a relatively small sequence of numbers that is used for encryption and decryption. At the same time, each of the parties exchanging information must know this key and keep it secret. A huge advantage of this approach is the encryption speed: the key, in fact, is a fairly simple and short instruction, which character, when, and which should be replaced. And this key works in both directions (that is, with it you can either replace all the characters with new ones, or return everything as it was), for which this encryption method was called symmetric. An equally huge minus is the fact that both parties, between which information is sent, must know the key.
Asymmetric Encryptioncomes a little trickier. Here, both we and our recipient already have two keys, which are called public and private. We and the recipient keep the private key (note that each person only stores his own key, which means that we already go beyond the very saying about two people who know it), and we and the recipient can easily pass the open one to anyone - our private, secret, it cannot be restored. In total, we use the recipient’s public key for encryption, and the recipient, in turn, uses his private key for decryption. The advantage of this approach is obvious: we can easily start exchanging secret information with different recipients, practically nothing (assuming the condition that our recipient did not lose / give his private key, etc., that is, did not pass it into the hands of a bad person), we do not risk when transmitting information. But, a huge minus can not do. And here it is as follows: encryption and decryption in this case are very, very, very slow, two to three orders of magnitude slower than similar operations with symmetric encryption. In addition, resources for this encryption are also spent significantly more. And the keys themselves for these operations are significantly longer than those for symmetric encryption operations, since it is necessary to secure the private key as much as possible from public selection. So, it is simply unprofitable to encrypt large amounts of information in this way. And the keys themselves for these operations are significantly longer than those for symmetric encryption operations, since it is necessary to secure the private key as much as possible from public selection. So, it is simply unprofitable to encrypt large amounts of information in this way. And the keys themselves for these operations are significantly longer than those for symmetric encryption operations, since it is necessary to secure the private key as much as possible from public selection. So, it is simply unprofitable to encrypt large amounts of information in this way.
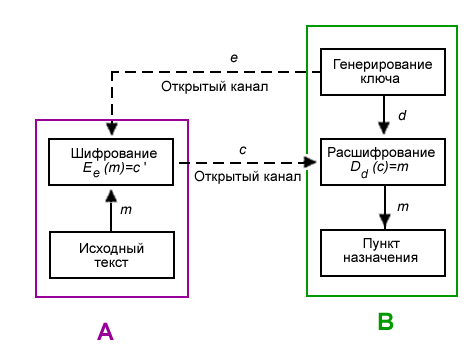
An example of using asymmetric encryption [Wikipedia]
e is the recipient’s public key B
d is the recipient’s private key B
m is the source information of the sender A
c is the encrypted source information
And again the question arises: what to do? And you need to do the following: take, and combineboth ways. Actually, this is how we get combined encryption. We encrypt our large amount of data by the first method, and in order to bring the key with which we encrypted it to the recipient, we encrypt the key by the second method. Then we get that even asymmetric encryption and slow, but the amount of encrypted data (that is, the key on which big data is encrypted) will be small, which means decryption will take place quickly enough, and then faster symmetric encryption will come into play.
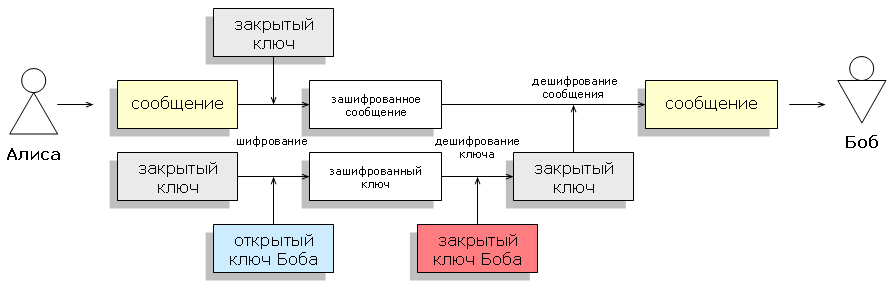
Application example of the combined system [Wikipedia]
All these mechanisms have found their application in practice, and both of our large camps PGP and S / MIME use them. As stated in the first article, asymmetric encryptionused for digital signature (namely, to encrypt our hash). The difference between this application and conventional asymmetric encryption is that our private key is used for encryption, and for decryption, the presence of the associated public key (that is, also ours) is sufficient. Since we do not hide the public key, our hash can be read by anyone, and not just an individual recipient, which is required for digital signing.
Combined encryption is used in both standards directly to encrypt the data sent.
Thus, starting to use digital signatures to protect our data from spoofing, we automatically (for these two standards) get a wonderful opportunity to protect our data from reading as well, which, you see, is very convenient.
Now that we have become acquainted with the general principles of the mechanisms used to protect our data, we can finally move on to practice and consider what to use. But more on that in the following articles.
Part 2
In this part, we will make a small digression from digital signatures towards that without which directly digital signatures, and information protection in the usual sense, would not be: encryption. After all, the first thing that comes to mind when it comes to protecting our data is not to give this data to a bad person to read. Therefore, before continuing to consider PGP and S / MIME standards, it’s worthwhile to fill out some of the blank spots in the knowledge and consider the encryption process in more detail.
Ciphers and codes exist, probably, from the moment humanity learned to record its impressions of the world around it on media. If you think about it a bit, even the ordinary alphabet is already a cipher. After all, when we read any text, in our head each drawn symbol is associated with a certain sound, a combination of sounds, or even a whole concept, and in the head of a neighbor who cannot read, this does not happen anymore.
Not knowing which symbol and what is compared, we can never understand what exactly the writer meant. For example, try to take and read something written in Hebrew, or in Chinese. The alphabets of these languages themselves will be an insurmountable obstacle for you, even if the concepts of your native language are written using these symbols.
But, nevertheless, just using someone else's alphabet is still not a sufficient measure to protect your data. Indeed, any alphabet, one way or another, was created for the convenience of using it and is inextricably linked with the language to which this alphabet is characteristic. So, having learned this language and a certain set of basic concepts in it (or simply using the services of a person who knows this language), a bad person can read your information.
So, you need to come up with an alphabet that only a limited circle of people know, and use it to write down information. Surely everyone read (or at least heard) a series of stories about Sherlock Holmes. An alphabet composed of dancing people appeared in this cycle (and many, I think, in childhood made up their own based on it). However, as this story shows, an observant person can figure out which symbol and what it refers to. So our information will fall into the wrong hands again.
What to do? Coming up more and more complex alphabets? But the more complex and cumbersome the alphabet, the more inconvenient to work with it, to keep it secret. In addition, there is a wonderful saying about secrecy: two people know - they know everything. After all, the weakest link in any cipher is a person who knows how to decrypt this cipher.
And why not make the encryption method immediately known to everyone, but it would be impossible to decrypt our data without some kind of key? After all, the key (unlike the entire alphabet) is small, it is quite easy to make a new one, if that (again, unlike the processing of the entire alphabet) is easy to hide. The most obvious advantages of key systems are shown in the following example: the recipient needs to read the message you sent. Plain, on paper. Let's say you use the secret alphabet. Then, in order to read the message, the recipient must know the alphabet, have a large dusty Talmud, which describes the decryption methods (because the alphabet must be complex in order to be reliable) and understand how to work with this Talmud. With the keys, everything is simpler: you put the message in the box with the lock, and the recipient just needs to insert the appropriate key, and know
So, well-known “alphabets” and keys are a mechanism that is much more convenient than just alphabets. But how is it possible to encrypt so that everything is decrypted with a simple key? And here, mathematics comes to our aid, and more specifically, mathematical functions that can be used to replace our original characters with new ones.
Recall what a function is. This is a certain ratio, according to which another can be obtained from one number. Knowing x and substituting it into the relation y = A * x known to us, we always get the value of y. But, as a rule, the opposite is also true: knowing y, we can get x.
As a rule, but not always. For many dependencies, getting y is easy, while x is already very difficult, and it takes a long time to get it. It is precisely on such dependencies that the encryption currently in use is based.
But back to the encryption itself. Encryption is divided into symmetric , asymmetric and combined . Consider the essence of each of them.
Symmetric EncryptionBy and large, it differs only slightly from the good old secret alphabet. As a matter of fact, it differs just in the presence of a key - a relatively small sequence of numbers that is used for encryption and decryption. At the same time, each of the parties exchanging information must know this key and keep it secret. A huge advantage of this approach is the encryption speed: the key, in fact, is a fairly simple and short instruction, which character, when, and which should be replaced. And this key works in both directions (that is, with it you can either replace all the characters with new ones, or return everything as it was), for which this encryption method was called symmetric. An equally huge minus is the fact that both parties, between which information is sent, must know the key.
Asymmetric Encryptioncomes a little trickier. Here, both we and our recipient already have two keys, which are called public and private. We and the recipient keep the private key (note that each person only stores his own key, which means that we already go beyond the very saying about two people who know it), and we and the recipient can easily pass the open one to anyone - our private, secret, it cannot be restored. In total, we use the recipient’s public key for encryption, and the recipient, in turn, uses his private key for decryption. The advantage of this approach is obvious: we can easily start exchanging secret information with different recipients, practically nothing (assuming the condition that our recipient did not lose / give his private key, etc., that is, did not pass it into the hands of a bad person), we do not risk when transmitting information. But, a huge minus can not do. And here it is as follows: encryption and decryption in this case are very, very, very slow, two to three orders of magnitude slower than similar operations with symmetric encryption. In addition, resources for this encryption are also spent significantly more. And the keys themselves for these operations are significantly longer than those for symmetric encryption operations, since it is necessary to secure the private key as much as possible from public selection. So, it is simply unprofitable to encrypt large amounts of information in this way. And the keys themselves for these operations are significantly longer than those for symmetric encryption operations, since it is necessary to secure the private key as much as possible from public selection. So, it is simply unprofitable to encrypt large amounts of information in this way. And the keys themselves for these operations are significantly longer than those for symmetric encryption operations, since it is necessary to secure the private key as much as possible from public selection. So, it is simply unprofitable to encrypt large amounts of information in this way.

An example of using asymmetric encryption [Wikipedia]
e is the recipient’s public key B
d is the recipient’s private key B
m is the source information of the sender A
c is the encrypted source information
And again the question arises: what to do? And you need to do the following: take, and combineboth ways. Actually, this is how we get combined encryption. We encrypt our large amount of data by the first method, and in order to bring the key with which we encrypted it to the recipient, we encrypt the key by the second method. Then we get that even asymmetric encryption and slow, but the amount of encrypted data (that is, the key on which big data is encrypted) will be small, which means decryption will take place quickly enough, and then faster symmetric encryption will come into play.

Application example of the combined system [Wikipedia]
All these mechanisms have found their application in practice, and both of our large camps PGP and S / MIME use them. As stated in the first article, asymmetric encryptionused for digital signature (namely, to encrypt our hash). The difference between this application and conventional asymmetric encryption is that our private key is used for encryption, and for decryption, the presence of the associated public key (that is, also ours) is sufficient. Since we do not hide the public key, our hash can be read by anyone, and not just an individual recipient, which is required for digital signing.
Combined encryption is used in both standards directly to encrypt the data sent.
Thus, starting to use digital signatures to protect our data from spoofing, we automatically (for these two standards) get a wonderful opportunity to protect our data from reading as well, which, you see, is very convenient.
Now that we have become acquainted with the general principles of the mechanisms used to protect our data, we can finally move on to practice and consider what to use. But more on that in the following articles.
