Additional dimensions: two-dimensional worlds
- Transfer
From the article on one-dimensional worlds, you know that the one-dimensional world is made up by the fact that its position is determined by one unit of information.
It should also be continuous (or close to continuous from a practical point of view). I described several examples of dimensions: income line, infinite, and represented by an infinite straight line; rainbow line, final, with bounding walls, represented by a segment; Aeolian wind direction line, finite-periodic, represented by a segment whose left end coincides with the right, or, equivalently, circle. Everyday, I mentioned another example - a world that is infinite in one direction, and finite in another. In another articleI emphasized that there are many types of measurements, but physical dimensions of space have unique and special (and also very obvious) properties that distinguish them from measurements of another type.
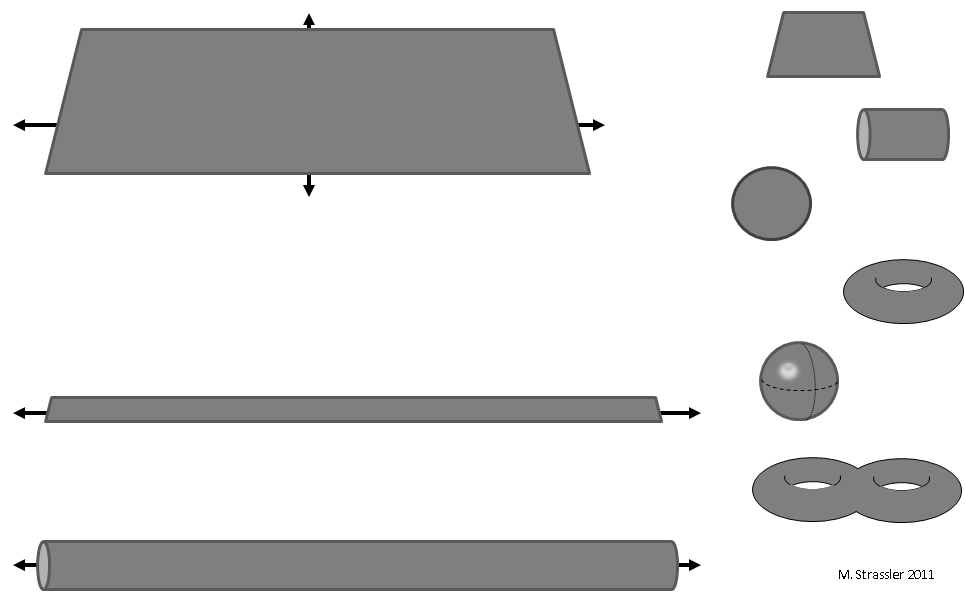
Fig. 1: two-dimensional worlds
What about two-dimensional worlds? It is not surprising that there are many more types of two-dimensional worlds than types of one-dimensional worlds. Some examples of such spaces are shown in fig. 1. You can imagine the world, infinite in both directions: the plane (top left). You can imagine a world that is infinite in one direction, and in the other it forms either a segment or a circle. Such worlds are naturally called a strip and a tube (bottom left). You can imagine the end world in both directions (right side of Fig. 1). And how many opportunities here! Only in this figure you can see a square from top to bottom, a cylinder (the round part of the can without lids and insides), a disk, a torus (something like a car tire), a sphere (only the surface), a double bus. And this is not all options. If you extrapolate into the future, it becomes clear that by the time
As with one-dimensional spaces, a position in a two-dimensional space is determined by two units of information.
An example of a sphere (with a good approximation) can be the surface of the Earth: any location can be designated by latitude and longitude. An ant walking along a garden hose moves along a two-dimensional pipe, and at any time is located at a certain distance from the crane and at a certain angle to the vertical. A multi-lane highway is essentially a two-dimensional strip with a very long side and a short side: two pieces of information needed to determine your position are the distance from the beginning of the road and the distance from its right edge.
Recall the revenue line. “Your last year’s income is a certain number in your local currency. It can be positive or negative, large or small; it can be represented as a point on the line, as in fig. 1, which we will call the "point of income." Every point on the line represents a possible income. ” If you are married, and you and your spouse have income, you can think of the two cash flows in your household as a two-profit plane. Two numbers describing a point on this plane will be your income and your spouse's income.
But a clever example of a torus showing how one can imagine interesting two-dimensional forms, whose dimensions are not dimensions of physical space. In fig. 3 articles about one-dimensional worlds, we saw that the possible wind directions form a one-dimensional world in the form of a circle (or a line, in which the beginning and end coincide). The possible directions of the sailing boat also form a similar circle. But everyone who sailed knows that it is not necessary to move in the same direction as the wind blows; if you set sail at an angle, you can move to the west, even if the wind blows from the north. So if I ask for two pieces of information - from which direction the wind is blowing, and in which direction is my sailing boat moving - both of them will be points on a circle. Two pieces of information, both located on a circle, represent a point on the torus.
Before continuing, I will mention the natural and widespread confusion. I have already hinted at it in the description of the various worlds given above. Do not confuse the dimensions of the forms themselves with a certain way of representing these dimensions or forms! The property of the circle is such that if you move along it in any direction, you will return to where you started. The circle has nothing inside or outside. Simply, the representation of a circle as a closed curve on a two-dimensional plane looks like it has an internal and external part. But this is simply a property of representing a circle on a plane, and not a property of the circle itself.
It should also be continuous (or close to continuous from a practical point of view). I described several examples of dimensions: income line, infinite, and represented by an infinite straight line; rainbow line, final, with bounding walls, represented by a segment; Aeolian wind direction line, finite-periodic, represented by a segment whose left end coincides with the right, or, equivalently, circle. Everyday, I mentioned another example - a world that is infinite in one direction, and finite in another. In another articleI emphasized that there are many types of measurements, but physical dimensions of space have unique and special (and also very obvious) properties that distinguish them from measurements of another type.

Fig. 1: two-dimensional worlds
What about two-dimensional worlds? It is not surprising that there are many more types of two-dimensional worlds than types of one-dimensional worlds. Some examples of such spaces are shown in fig. 1. You can imagine the world, infinite in both directions: the plane (top left). You can imagine a world that is infinite in one direction, and in the other it forms either a segment or a circle. Such worlds are naturally called a strip and a tube (bottom left). You can imagine the end world in both directions (right side of Fig. 1). And how many opportunities here! Only in this figure you can see a square from top to bottom, a cylinder (the round part of the can without lids and insides), a disk, a torus (something like a car tire), a sphere (only the surface), a double bus. And this is not all options. If you extrapolate into the future, it becomes clear that by the time
As with one-dimensional spaces, a position in a two-dimensional space is determined by two units of information.
An example of a sphere (with a good approximation) can be the surface of the Earth: any location can be designated by latitude and longitude. An ant walking along a garden hose moves along a two-dimensional pipe, and at any time is located at a certain distance from the crane and at a certain angle to the vertical. A multi-lane highway is essentially a two-dimensional strip with a very long side and a short side: two pieces of information needed to determine your position are the distance from the beginning of the road and the distance from its right edge.
Recall the revenue line. “Your last year’s income is a certain number in your local currency. It can be positive or negative, large or small; it can be represented as a point on the line, as in fig. 1, which we will call the "point of income." Every point on the line represents a possible income. ” If you are married, and you and your spouse have income, you can think of the two cash flows in your household as a two-profit plane. Two numbers describing a point on this plane will be your income and your spouse's income.
But a clever example of a torus showing how one can imagine interesting two-dimensional forms, whose dimensions are not dimensions of physical space. In fig. 3 articles about one-dimensional worlds, we saw that the possible wind directions form a one-dimensional world in the form of a circle (or a line, in which the beginning and end coincide). The possible directions of the sailing boat also form a similar circle. But everyone who sailed knows that it is not necessary to move in the same direction as the wind blows; if you set sail at an angle, you can move to the west, even if the wind blows from the north. So if I ask for two pieces of information - from which direction the wind is blowing, and in which direction is my sailing boat moving - both of them will be points on a circle. Two pieces of information, both located on a circle, represent a point on the torus.
Before continuing, I will mention the natural and widespread confusion. I have already hinted at it in the description of the various worlds given above. Do not confuse the dimensions of the forms themselves with a certain way of representing these dimensions or forms! The property of the circle is such that if you move along it in any direction, you will return to where you started. The circle has nothing inside or outside. Simply, the representation of a circle as a closed curve on a two-dimensional plane looks like it has an internal and external part. But this is simply a property of representing a circle on a plane, and not a property of the circle itself.
